舰艇抗沉过程的多智能体仿真模型

吴向君，侯岳，浦金云

（海军工程大学舰艇安全技术系，湖北武汉 430033）

0 引言

舰艇受到武器攻击后，大量舱室会破损进水，严重时还会导致舰艇的沉没。因此，良好的舰艇抗沉性是保证舰艇生命力的基础。目前国内在对抗沉性进行设计和仿真时，一般只考虑舰艇结构自身能承受的被动抗沉能力，而没有考虑舰员在抗沉过程中的主动抗沉能力［1］。然而，对于大型水面舰艇而言，由于其配置了较多的抗沉设备、设置了较多的抗沉战位，因此，其抗沉过程组织和实施的好坏，直接影响着舰艇的抗沉性以及舰艇的生命力［2］。

很显然，在大型舰艇抗沉性设计时，已经迫切需要对抗沉过程进行建模和仿真，分析抗沉过程的抗沉效能，找出影响抗沉效能的关键环节。

目前，国内外对抗沉过程的仿真均鲜见报道。文献［3］对消防过程的仿真方法进行了介绍。抗沉过程和消防过程二者的相同点是:①都属于离散、动态和交互过程;②都是舰艇上重要的损害管制过程;③目的都是仿真干预效能，找出关键环节。不同点是过程的组织特点、参与的智能体不同。

文献［3］虽然使用多智能体较成功地完成了消防过程的仿真，然而抗沉过程的多智能体仿真显得更为困难。这是因为:①抗沉过程的组织协调非常复杂，多Agent仿真组织模型的建立和仿真过程的控制将更加困难;②抗沉人员需要比消防人员具有更大的自主性和智能型，即单Agent的推理模型设计将更为复杂。

基于此，本文将使用多智能体技术模拟抗沉人员的思维和交互过程，实现抗沉过程的仿真。

1 抗沉过程的多智能体构成

任何独立的能思想并可以同环境交互的实体都可抽象为智能体。1个智能体主要包含3个方面的属性，即感知属性、动作属性和推理模型。多个智能体之间进行交互和通讯就可以组成多智能体［4］。

由于舰艇的抗沉过程是根据舰艇的实际进水灾害现象，由损管指挥中心统一指挥，各类抗沉人员之间相互合作、交流并且不断调整的过程;因此，这个过程也可看作是多个智能主体相互协作和通讯的过程。

抗沉过程仿真的多智能体模型包括抗沉指挥中心智能体（C-Agent）、堵漏人员智能体（J-Agent）、舱室排水人员智能体（D-Agent）、液舱调整决策智能体（L-Agent）和进水灾害模拟智能体（F-Agent）。

J-Agent和D-Agent负责向抗沉指挥中心汇报相关信息，并执行其相关指令，但它们自身没有推理模型。这2个智能体的反应时间直接影响着抗沉过程的进程。F-Agent用于根据舱室破损情况和初始漂浮姿态，模拟仿真舱室的进水过程以及舰艇不沉性参数;属于纯反射性智能体。

下文主要针对2个较为复杂的智能体（C-Agent和L-Agent）的相关属性进行详细介绍。

2 抗沉指挥中心智能体及其推理模型

抗沉指挥中心智能体C-Agent从F-Agent中获取当前舰艇进水信息，通过推理计算，给J-Agent，DAgent和L-Agent下达动作指令。C-Agent负责着整个抗沉过程的调度和整体决策，其模型属性详细介绍如下。

2.1 感知属性和动作属性

C-Agent的感知属性包括当前破损舱室名称、破口面积、破口位置、当前排水设备排水量和舰艇当前不沉性参数（横倾角、纵倾角、船中吃水等）。

动作属性包括:①告知J-Agent是否执行堵漏动作，并告知其允许的最大反应时间。②告知DAgent是否动作。③告知L-Agent是否动作。

2.2 推理模型

2.2.1 推理所需信息参数的计算模型

推理模型所需的信息参数主要包括最大可以堵住的破口半径Rm（m）、堵漏人员允许的最大反应时间Tm（s）、排水设备能排出的最大破口半径Rpm（m）。其计算模型如下:

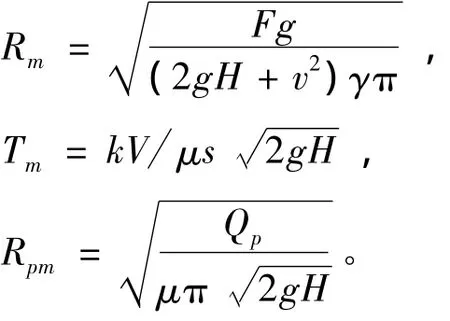
式中:F为所有堵漏人员最大作用力，t;H为破口中心所在的水下深度，m;v为舰艇航速，m/s;γ为海水密度，t/m3;g为重力加速度，m/s2;s为破口面积，m2;V为舱室体积，m3;μ为流量系数;k为舱室渗透系数;Qp为可用的排水流量，m3/s。

2.2.2 基于专家系统的推理模型

基于专家系统的推理模型由产生式规则库和推理机构成，它们构成了C-Agent的思维中心，用于对各种抗沉措施进行集中调度和管理。由于推理机的设计技术较为成熟，因此，产生式规则库就成为了推理模型的核心部分［4］。

建立的产生式规则部分示例如下:

1）如果破口半径小于Rm及J-Agent的反应时间小于Tm，则告知J-Agent开始运行;

2）如果可用的排水流量Qp为0，则告知DAgent不需运行;

3）如果当前舰艇不安全，则告知L-Agent开始运行。

推理模型首先对推理所需的信息参数进行计算，然后匹配产生式规则库，生成抗沉方案;并根据匹配结果，告知其他智能体是否动作。

3 液舱调整决策智能体及其推理模型

舰艇受损进水后，一般会产生倾斜和倾差。通常可以通过调整不同位置的液舱装载量，以消除倾斜和倾差，平衡舰体。

3.1 感知属性和动作属性

L-Agent的感知属性包括舰艇当前的姿态参数、当前未破损的液舱名称以及各个液舱的装载状态。这些数据分别从F-Agent和外界环境获得。其动作属性是生成并实施多步液舱调整方案。

3.2 推理模型的建模思路

液舱的调整方案包括单步调整方案和多步调整方案。单步调整方案是指单舱的压载、卸载和2个舱之间的移载。然而，在舰体的扶正过程中，有时仅靠一步或者说单步液舱调整方案，很难达到舰体扶正的目的。因此，需要将多个单步液舱调整方案进行优化选取和优化组合，以形成最优的多步液舱调整方案。

考虑到单步液舱调整方案只是多步液舱调整方案的1种特殊情况，因此，液舱调整决策智能体的推理模型主要是指多步最优的液舱调整方案生成模型。由于建立单步液舱调整方案集，是建立多步最优液舱调整方案生成模型的基础，因此，下文将首先对其进行介绍。

3.3 单步液舱调整方案集生成算法

分别用φS1，φS2和φS3表示单步调整方案的可压载空间集、可卸载空间集和可移载空间集。

3.3.1 液舱属性集

在制定液舱调整方案集时，对于任意1个液舱都主要包含3个属性，属性取值含义如表1所示。

表1中的US属性值是为了避免调整方案搜索过程的重复进行。当某个液舱已经在某单步液舱调整方案中出现，则此液舱的US属性值为1;在以后的搜索空间中将不再把此液舱作为可以使用的备选液舱。US属性主要被用在第3.4.2节的多步最优调整方案生成算法中，以保证每个液舱只被使用1次，避免搜索的重复进行。

3.3.2 单步液舱调整方案集的生成算子

假设C表示液舱，C（FE），C（KD）和C（US）分别表示液舱C的FE，KD和US属性的值。则:表示所有可以移载的舱室对集合，即可移载空间集。单步调整方案集

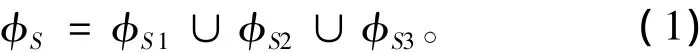
3.4 多步最优液舱调整方案的生成模型

多步最优液舱调整是一个全局最优求解的问题。由于多步最优调整方案是由有限个单步最优调整方案构成，因此，只要能实现每个单步最优调整的局部最优化，即可实现多步最优调整的全局最优化求解［5］。

3.4.1 单步最优调整方案选取算法

式（1）给出的单步调整方案集一般包含多种方案，部分方案可能并不能较好地达到扶正舰体的目的。因此，下文首先根据抗沉原理，建立启发式筛选规则，从定性的角度，筛选出较优的调整方案;然后，通过在筛选后的方案集中建立最优选取算法，从定量的角度，选择最优的液舱调整方案。

1）启发式规则

假设某舰艇纵剖面图及其分区情况如图1所示，可以建立下列启发式规则示例。

规则1:如果舰艇产生首倾和左倾，则可以选取的液舱调整方案包括:将Z1区的液舱导移至Y3区，或者将Z1区的满液舱卸空，或者将Y3区的空液舱加满。

规则2:如果舰艇产生尾倾和右倾，则可以选取的液舱调整方案包括:将Y3区的液舱导移至Z1区，或者将Y3区的满液舱卸空，或者将Z1区的空液舱加满。

上述启发式规则还有很多，本文不再罗列。启发式规则的建立，明显缩小了调整方案空间的大小。然而，经过筛选后的调整方案仍然会有多个，因此，下面介绍从中进行优选的方法。

图1 舰艇纵剖面图Fig．1Ship longitudinal section

2）基于改进TOPSIS的优选算法

传统TOPSIS方法又被称为逼近理想解排序法，是1种常用的多属性问题的评估决策方法。该方法存在一定的缺陷。例如，假设待决策空间中存在2个点A1和A2，如果A1距理想点的距离比A2距理想点的距离近并且同时A1距负理想点的距离也比A2距负理想点的距离近，此时二者的优劣排序就遇到了困难。

基于此，文献［6］的作者对传统TOPSIS的改进算法进行了介绍，并结合文献［7］的研究成果，通过分析得出结论:用垂面距离代替传统方法中的欧式距离，可以改善传统TOPSIS方法的不足之处。因此，本文将使用基于垂面距离的改进TOPSIS算法建立最优液舱调整方案的选取模型，详细步骤如下。

步骤1:建立衡量调整方案优劣的属性集。

本文使用横倾角绝对值θ、稳度储备系数C和最小干舷F来表示各个液舱调整方案实施后的不沉性指标［8］。其中横倾角是成本型指标，越小越好;稳度储备系数和最小干舷是效益型指标，越大越好。

步骤2:建立最优方案选取决策矩阵L=（lij）N×3。

式中:N为使用启发式规则筛选后的备选调整方案集个数;θi，Ci和Fi分别为第i个调整方案实施后的对应不沉性指标;w1，w2和w3分别为θ，C和F的权重。文献［8］采用最小平方法确定上述指标的权重;文献［9］采用相对比较法确定权重。由于权重确定问题不是本文重点讨论的问题，因此，综合以上的研究结果以及专家的建议，本文认为3个指标的权重都为1/3。

步骤3:建立理想解K+，并对最优方案选取决策矩阵L进行平移计算。

步骤6:计算各个液舱调整方案与理想解之间的相对远离度Fi。

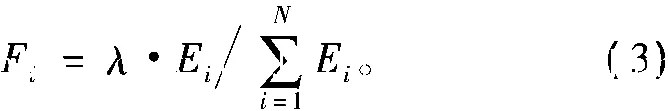
对应Fi最小的液舱调整方案，即是最优的液舱调整方案。λ表示放大系数，以便于比较观察。

3.4.2 多步最优液舱调整方案的生成算法

经过启发式规则筛选后，假设当前可以使用的空水舱数量、满水舱数量、空油舱数量、满油舱数量分别为WE0，WF0，OE0，OF0。用WEi，WFi，OEi，OFi表示第i步单步液舱调整后，未被使用过的空水舱数量、满水舱数量、空油舱数量、满油舱数量。多步最优液舱调整方案的生成算法见图2所示。

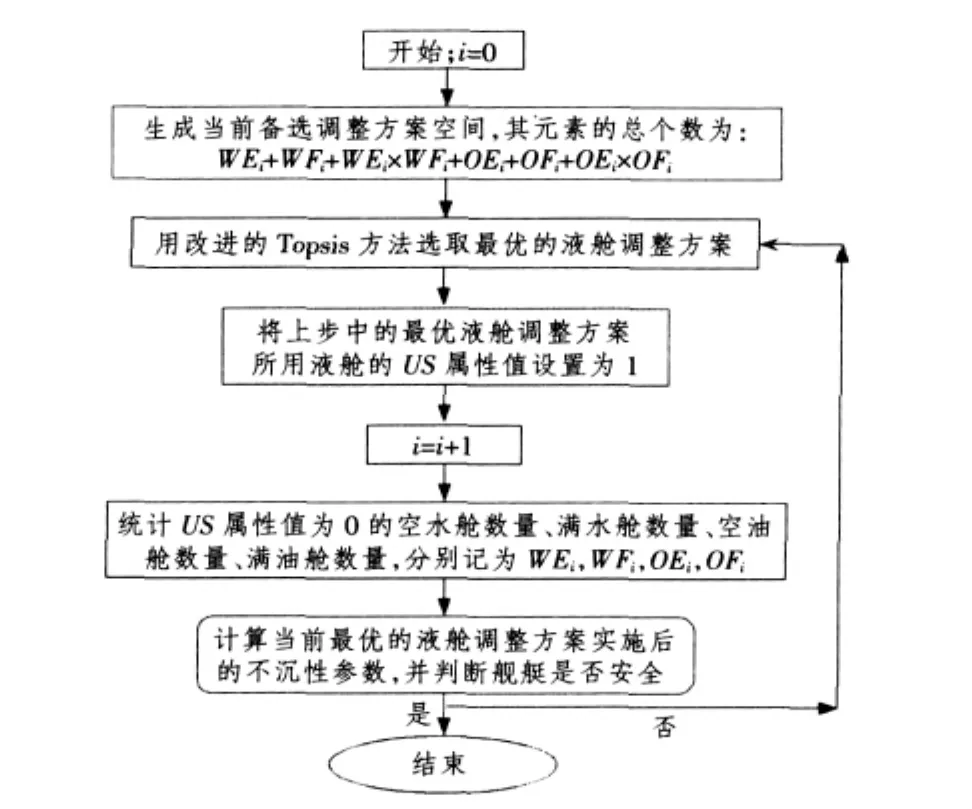
图2 多步最优液舱调整方案生成算法Fig.2Generation arithmetic of multi-step optimal liquid cabin adjustment plans

4 抗沉过程仿真的TPN模型

舰艇的抗沉仿真过程是多个智能体相互通讯、协调和影响的过程。这一过程主要反映在多智能体在时序仿真分析的组织上。文献［3］使用事件树对消防过程的仿真进行了组织，然而，事件树并不能反映过程的时间特征。为了弥补这一不足，本文将使用带有明显时序特征的时延Petri网（TPN）模型来组织仿真过程。

4.1 TPN模型

Petri网是一种图形化、数学化的建模工具，是对复杂过程建模和仿真所采用的一种广泛使用的方法［10］。

4.2 基于TPN的抗沉过程仿真模型

建立的某抗沉过程多智能体仿真的时延Petri网模型如图3所示。其中，细矩形框表示时延变迁，细线条表示非时延变迁。图3中只有P7令牌容量为无限大，其他库所容量都为1。

图3中主要库所和变迁的含义，分别如表2所示。部分中间库所和非时延变迁未进行标记。

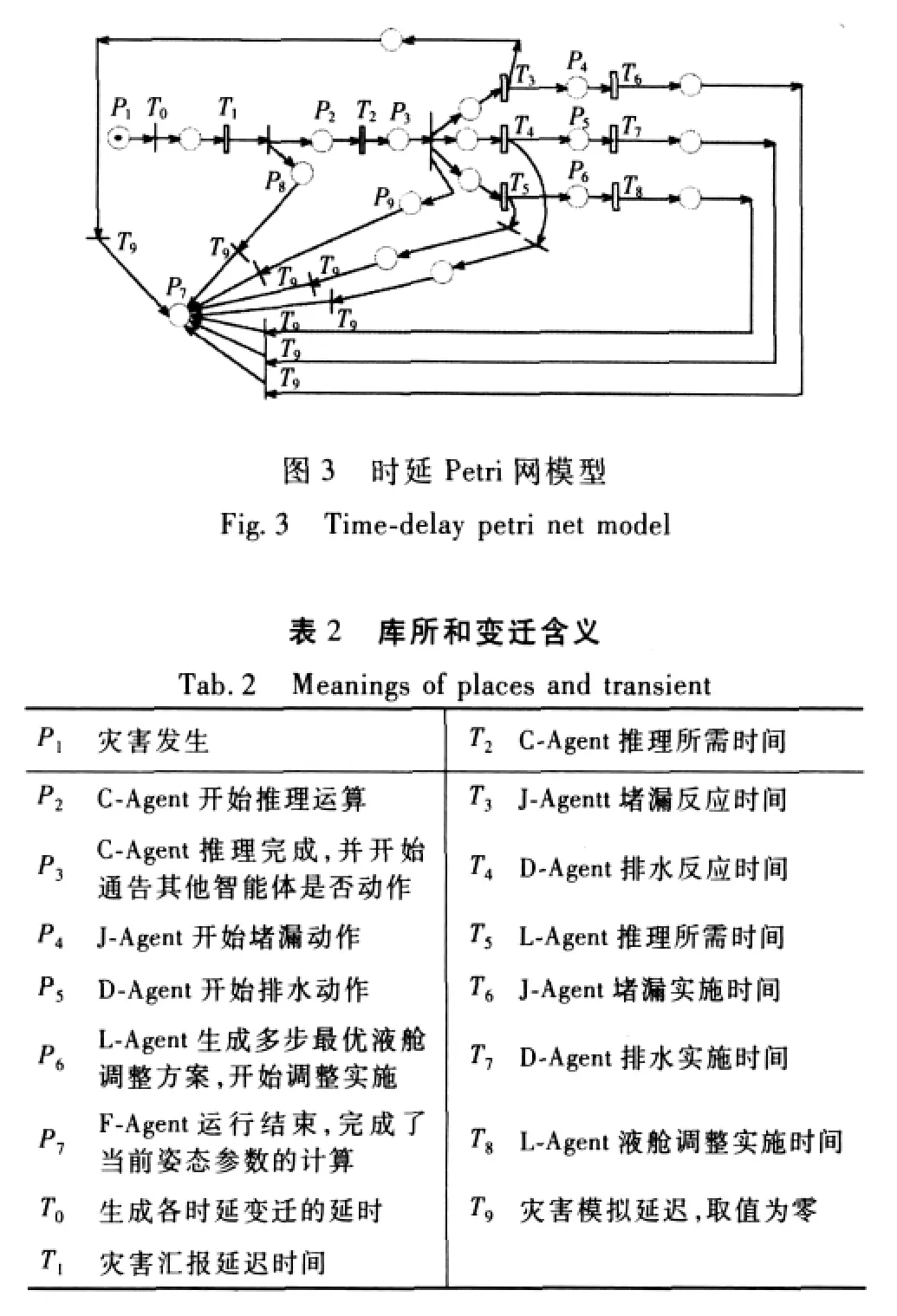
4.3 基于TPN的抗沉过程仿真算法

图3描述了抗沉过程的组织进程以及J-Agent，D-Agent，C-Agent，L-Agent和F-Agent的异步并发特征;可以按照下述算法进行仿真的组织运行。

1）设置当前仿真时钟t为0 s，清空“待激发变迁表”Fetable;

2）按照TPN的激发规则和当前库所的状态，将当前将要被激发的变迁以及其对应的激发时间点添加到Fetable中;

3）从Fetable中抽取最早将要激发的变迁，并对其进行激发处理，修改当前仿真时钟t为此变迁的激发时间点，修改TPN网中库所的状态并调用此变迁对应的智能体推理模型;

4）判断Fetable中是否还存在着可能被激发的变迁，如果存在，则跳至2）;如果不存在，则仿真结束。

5 仿真实例

5.1 灾害场景及仿真初始参数设置

假设某破坏直径为10 m的鱼雷在某船长方向+15 m处爆炸;爆炸后舱室A和B出现大破口并进水，舱室B和C之间的舱壁出现小破口，破口半径为20 cm，破口面积为0.12 m2，破口流量系数为0.8，破口中心距离基线高度为3 m;舱室C排水泵失效;舰艇丧失航行能力，即航速为0。如图4所示。

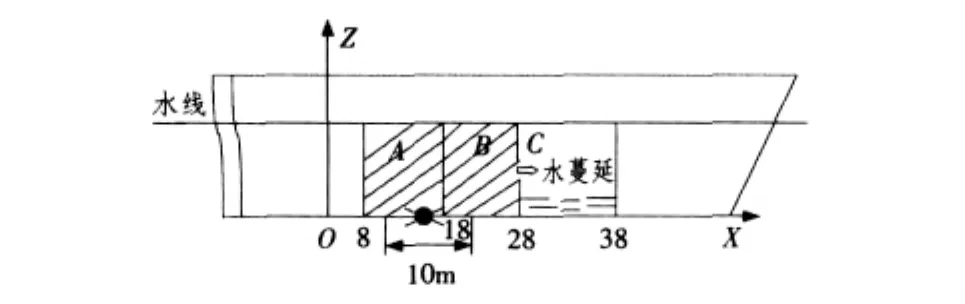
图4 战损案例设定图Fig.4Damage condition enactment

当T0变迁发生后，假设生成的T1，T2，T3，T4，T5，T6，T7，T8的延时分别为5 s，8 s，7 s，9 s，10 s，20 s，15 s，30 s。

5.2 仿真结果

5.2.1 智能体激发时序图

根据第2.2.1节的信息参数计算模型，C-Agent通过计算得出:Rm=25 cm，Tm=30 s，Rpm=0 m。

在此基础上，根据第2.2.2节的产生式规则库，C-Agent对其他各个智能体的动作通告情况如下:

①只有B和C之间的舱壁破口可以进行堵漏，通知J-Agent开始堵漏。②D-Agent不需动作。③通知L-Agent开始制定最优液舱调整方案。

按照图3的仿真组织模型和第4.3节的仿真算法，可以得到各个智能体的激发状态随时间变化的情况，见图5。图5中D-Agent始终未被激发，这是因为C-Agent通告其不需要动作。

图5 智能体激发状态时序图Fig.5Excitation sequence of agent

图5中的各个重要时间节点所发生的事件见表3。

5.2.2 液舱调整决策智能体仿真计算结果

在图5中，当仿真时钟为5+8+10=23 s，变迁T5激发完成，液舱调整决策智能体制定出最优液舱调整方案。根据第3.3节和第3.4节的最优液舱调整方案生成算法，其推理过程如下:

当前空液舱的个数为4，满液舱的个数为6。因此，可压载空间集的元素个数为4，可卸载空间集的元素个数为6，可移载空间集的个数为24个，共有34个单步液舱调整方案。

然而，由于当前舰艇产生了左倾和首倾，通过匹配第3.4.1节的启发式规则库，可得可压载空间集的元素个数为2，可卸载空间集的元素个数为3，可移载空间集的个数为6个，共有11个单步液舱调整方案。通过计算，这11个单步液舱调整方案与理想解之间的相对远离度如图6所示，横轴为方案序号，纵轴为相对远离度（第3.4.1节中，式（3）的λ取100）。

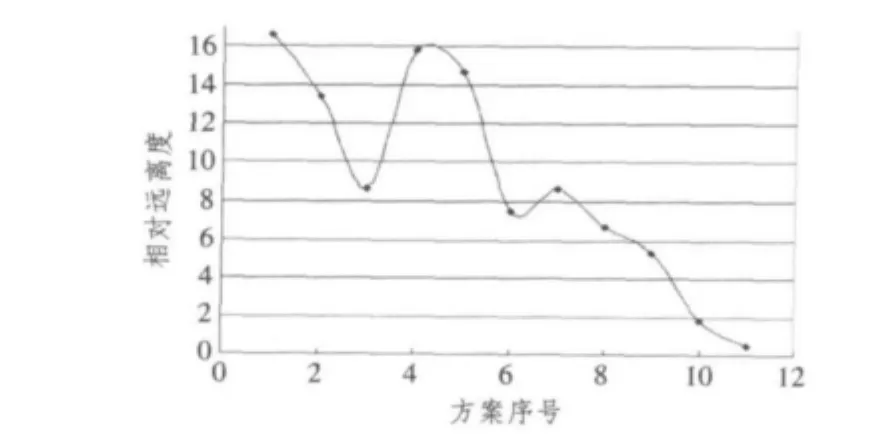
图6 方案相对远离度Fig.6Distance between plans

根据图6和第3.4.2节的多步最优调整方案生成算法，可以得出使用2步液舱调整方案，就可使舰艇恢复安全。2步液舱调整方案为方案11和方案8。对应的具体液舱调整方案为:液舱C5移载至液舱C3;液舱C7移载至液舱C8。

值得提出的是，单步调整方案10和方案9虽然都比方案8好;但由于这2个方案分别使用到了液舱C5和液舱C3，而液舱C5和液舱C3已经在方案11中使用过，因此，根据US属性值的设置原理，不能将方案10和方案9作为第二步调整方案使用。

5.2.3 舰艇横倾角和纵倾角变化时域图

图3中的进水灾害模拟智能体（F-Agent）计算出了整个仿真过程中，舰艇横倾角和纵倾角随时间变化的时域图如图7所示。

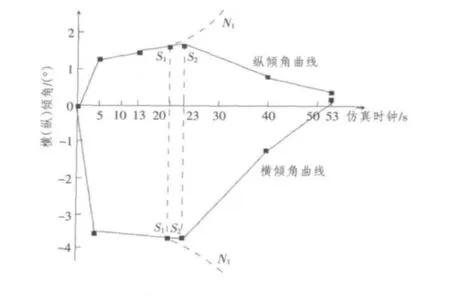
图7 横倾角和纵倾角变化时域图Fig.7Heel angle and trim angle in time domain

5.3 仿真结果分析

通过分析可发现影响上述仿真过程的3个关键环节:

1）J-Agent开始堵漏时间（图7中的S1点）。开始堵漏时的时间T1+T2+T3必须小于堵漏人员允许的最大反应时间Tm。在本案例中，T1+T2+T3的值必须小于30 s，如果大于30 s，则舱室C将会完全进水，F-Agent仿真计算发现，此时舰艇将发生沉没，如图7中的S1－N1线所示。当T1+T2+T3的值小于30 s时，其取值越小，舰艇在经过液舱调整后的纵倾角越小。

2）舱室C的排水能力。保证舱室C足够的排水能力关系着整个抗沉过程的成败。如果舱室C中排水泵的排水能力大于破口流量，则海水同样不会造成舱室C进水，此时，即使堵漏失败，舰艇也不会沉没。因此，需要加强舱室C排水泵的生命力设计，以免攻击后丧失排水能力。

3）液舱对船体的平衡能力。在堵漏实施成功之后，如果不通过液舱调整，则舰艇虽然能漂浮，但舰艇仍然会有较大的横倾和纵倾，这对舰艇的不沉性依然不利。图7中从S2点开始，进行了液舱的调整，最终大大减小了S2点的横倾角和纵倾角，扶正了舰体，提高了不沉性。

6 结语

舰艇的抗沉过程是一个复杂的异步并发过程;通过对抗沉过程进行仿真分析，可以找出影响整个抗沉过程的关键环节。目前，国内外对抗沉过程仿真的研究报道极少。

基于此，本文在建立关键智能体的推理模型、抗沉过程仿真模型的基础上，较好地解决了抗沉过程多智能体仿真模型的构建问题。通过实例计算，不仅验证了此仿真模型的准确性，还找出并分析了影响抗沉过程的3个关键环节。

本文建立的仿真模型和抗沉关键环节的分析结果，为舰艇抗沉性的设计和评估提供了一定的方法和结论支撑。

［1］浦金云．舰船生命力［M］．北京:国防工业出版社，2008．

［2］浦金云，金涛．舰艇损管组织指挥［M］．北京:国防工业出版社，2008．

［3］ANDRADE S F，et al．Analysis of shipboard firefightingteam efficiency using intelligent-agent simulation［Z］．Brazilian Navy．

［4］蔡自兴，徐光佑．人工智能［M］．北京:清华大学出版社，2004．

［5］谢政．非线性最优化［M］．长沙:国防科技大学出版社，2003．

［6］叶云，屈洋，等．改进TOPSIS法的武器系统WTSC问题决策［J］．火力与指挥控制，2005，30（S1）:137－139．

［7］华小义，等．基于“垂面距离”的TOPSIS法——正交投影法［J］．系统工程理论与实践，2004，（1）:114－119．

［8］浦金云，等．专家系统和多目标决策理论在抗沉决策系统中的应用［J］．海军工程大学学报，2000，（1）:83－86．

［9］OICER A I，MAJUMDER J．A case-based decision support system for flooding crises onboard ships［J］．Quality and Reliability Engineering International，2006，22:59－78．

［10］康凤举．现代仿真技术与应用［M］．北京:国防工业出版社，2001．117－118．