减摇水舱挡板开度对稳定矩影响的研究

蒋 颉 丁 勇

1中国舰船研究设计中心，上海 201108

2哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

减摇水舱挡板开度对稳定矩影响的研究

蒋 颉1丁 勇2

1中国舰船研究设计中心，上海 201108

2哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

水舱阻尼是影响减摇水舱减摇性能的重要因素，在减摇水舱的工程应用中，如何获得最佳的水舱阻尼成为水舱设计最关键的环节之一。一般情况下，可以通过调节水舱挡板来改变水舱底部通道截面积的大小，以达到改善水舱阻尼的目的。本文利用FLUENT软件，计算了二维水舱模型中不同挡板开度条件下水舱稳定矩的变化，得到该仿真模型最佳阻尼所对应的挡板开度的参考数值，并与减摇水舱台架试验的结果进行比较，表明了利用数值仿真的方法来研究水舱阻尼是可行的，该数值仿真的结果是合理的。

减摇水舱；挡板开度；FLUENT；数值仿真

1 引言

减摇水舱最大的优点是其在任何航速下均有一定的减摇效果，这使得减摇水舱被广泛应用，如航母、LPD舰以及客船、集装箱船、巡逻船、海洋救生船、科学考察船等。水舱阻尼成为影响水舱减摇性能的重要因素：小的水舱阻尼，得不到理想的减摇效果，并且有可能使共振区外的横摇增大；大的水舱阻尼也会降低水舱的减摇效果。由此可见，选择适当的水舱阻尼，才能得到较大的水舱稳定矩，才能保证水舱具有良好的减摇性能。同时，为了使减摇水舱在较宽的海浪频率范围内均有满意的减摇效果，可以通过调节安装于水舱底部连通道的阻尼挡板来改变流道局部截面积的大小，达到调节水舱阻尼、增强水舱减摇性能的目的［1－5］。

通常，利用台架试验来研究减摇水舱性能。试验台架是1个满足运动相似和动力相似的复重力摆，也是对水舱减摇性能进行研究的重要手段。然而，随着对减摇水舱研究的深入，发现对于水舱的非线性特性，特别是在饱和效应出现时，进行台架试验存在着一些困难。如在船模上安装一个“小”的水舱模型要涉及到水动力和实际特性是否可行的问题；再如水舱模型太小，则尺度效应非常明显，试验结果可靠度不高［6］。同时，近年来随着计算机技术的飞速发展，一些科研人员开始使用CFD（Computational Fluid Dynamics）的方法来研究减摇水舱的流体特性，弥补了理论计算研究和船模实验的不足，充分利用计算机仿真技术成为了研究水舱性能的一个重要方向。本文利用FLUENT软件针对不同阻尼挡板开度条件下减摇水舱舱液瞬态运动进行了二维数值仿真，监测并得到了水舱稳定矩的变化情况，与台架试验的结果相比较后获得了一致的结论。

2 数值仿真的模型尺度

二维水舱模型的几何尺度如图1所示。

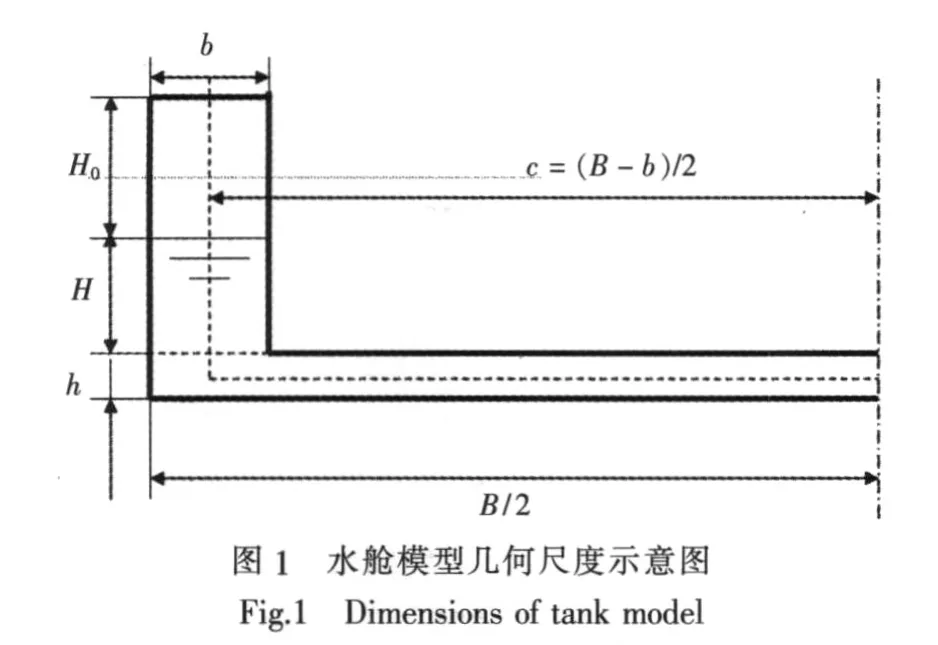
图中，h为水舱底部通道高度；H为边舱液位高度；B为沿船宽方向的长度；b为边舱宽度；c为边舱中心线至船纵中剖面的距离。

某船根据相似律进行折算后，转动惯量J为429 kg·m2，阻尼系数 NN为 85.1 N·m·s，恢复力矩Dh为 1 690.8 N·m，模型比尺 λ 取 8.5［7］，模型具体的几何尺度数据如表1所示。

表1 减摇水舱模型尺寸Tab.1 Dimensions of anti-rolling tank

3 仿真模型的建立与计算网格的划分

利用FLUENT的专用前处理软件包GAMBIT为数值仿真建立二维计算模型并划分网格。

3.1 仿真模型的建立

为了与台架试验的试验结果相比对，文中共建立11个仿真模型，分别对应于阻尼挡板开度为0、1／5、3／10、2／5、9／20、10／20、11／20、3／5、7／10、4／5、1。为了保证各模型的仿真计算结果具有可比性，建立的11个计算模型，除阻尼挡板的开度不同以外，几何尺度均一致，边界条件的设置和网格划分的方法也都相同。图2为阻尼挡板开度为10／20时的数值模拟模型。

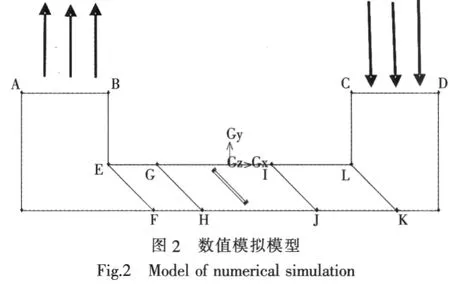
图中，EF、GH、IJ、KL 是为了细化网格、 提高网格质量而设置的辅助线。

边界条件是计算域的边界上所求解的变量或其一阶导数随地点及时间变化的规律，是CFD数值模拟有定解的必要条件，只有给定合理的边界条件才可能计算出流场的解［8-9］。文中数值模拟模型计算域的边界有入口条件、出口条件及壁面条件。如图2所示，该模型中，CD设置为速度入口边界条件 （Velocity＿inlet）；AB设置为自由出流边界条件（Outflow）；考虑到粘性的影响，除 AB、CD以及4条辅助线以外的所有边界线均设置为固壁边界条件（Wall）。在以上的各个边界条件中，最关键的是速度入口边界条件的设置，初始入口速度设置的过大或过小，都会影响到仿真计算结果的正确性。文中设置仿真模型的初始入口速度为0.05 m／s。根据减摇水舱的工作机理，当船体受波浪扰动作用产生横摇、舱壁与船体同步横摇时，由于舱液惯性的存在，舱液并没有立即移动也没有立即形成液位差，但在惯性力的作用下已产生初始运动速度。此状态的时间较短，设置的初始速度大不符合舱液运动的实际状态，也得不到所需的仿真结果；设置较小的初始速度时，计算求得横摇稳定矩的数值较小，不利于寻求水舱最佳阻尼所对应的阻尼挡板的开度情况。

3.2 计算网格的划分

几何模型是网格和边界的载体，网格是CFD模型的几何表达方式，也是数值计算与分析的载体。网格质量好坏将直接影响到数值模拟的精度和效率［10］。事实上，在采用CFD技术模拟水舱舱液流动的过程中，模型的建立和网格的划分将花费整个工作60%以上的时间。文中使用非结构网格来离散计算域。考虑漩涡的影响，阻尼挡板附近计算域的网格划分是整个模型网格划分的重点，因为阻尼挡板的存在使得水舱底部通道截面积的大小发生了改变，也使得流体在流经该区域时会出现旋涡区或者会出现速度分布的改变，导致流动的阻力大大增加，从而引起比较集中的能量损失。以阻尼挡板开度为10／20为例，利用4条辅助线将整个计算域分为4个区域，通过设置边界壁控制点间距大小，控制区域网格密度大小，分别对各个区域进行网格划分，总的网格数目为73 560。其中，阻尼挡板附近的计算域网格密度最大，网格单元数为23 866，占总数的32%；其次是IJKL面域网格密度，网格单元数为10 178；再其次是EFGH面域的网格密度，网格单元数为9 430。这种网格划分方式即可保证求解问题所要求的精度。图3所示为划分好的阻尼挡板开度为10／20时的计算网格，图4所示为位阻尼挡板开度为10／20时阻尼挡板附近的局部计算网格示意图。为保证仿真计算能够准确模拟阻尼挡板附近的舱液运动，该处的计算网格设置为三角形网格，节点间距设置为2 mm，网格密度较其他部分稍密。

对于网格数问题，应该以能否得到满足精度要求的计算结果为准，一味地追求细密性网格不一定能满意地解决问题。一方面，在网格尺度达到某一下限值后，解对网格精度的变化不再敏感，甚至有可能使解的计算精度变差［11］；另一方面，由于计算机硬件方面的限制，数目较大的计算网格需要耗费更长的计算时间，降低了仿真试验计算效率和适用性。针对计算网格数目与计算时间的关系研究：以阻尼挡板开度为10／20为例，求得计算网格数目分别为 12 387、23 657、42 896、58 934、73 560、100 546、154 862、198 723 时所耗用的计算时间，其计算时间分别为112 min、156 min、198 min、264 min、375 min、644 min、898 min、1 197 min。图5所示为计算网格数目与计算时间的关系曲线。由图可见，计算网格数目为73 560时花费375 min；当计算网格数目大于73 560时，计算机进行仿真模拟所耗用的时间几乎是计算网格数目为73 560时花费时间的数倍。

4 仿真计算与结果分析

4.1 湍流模型

由水舱的减摇机理可知［4］，实际水舱中液体的流速和管道直径都比较大，因此舱内流体的流动状态几乎都是湍流。本文采用湍流模型计算，文中选用理论上发展较为完善，对湍流模型求解在工程上广泛运用的k－ε二方程湍流模型来封闭RANS 方程，湍动能 k 方程为［8］：

式中，C1=1.44；C2＝ 1.92；σ1＝ 1.0；σ2＝ 1.3。

通过湍流运动粘度υt建立了Reynolds应力与平均速度梯度的关系，使得控制方程封闭。υt表示成 k 和 ε 的函数，即υt＝Cμε2／k，Cμ为经验常数，Cμ＝ 0.09。

4.2 仿真计算

为了能够与台架试验的实验结果直接进行比较，文中定性地计算了舱液流速为0.05 m／s条件下不同阻尼挡板开度时的水舱稳定力矩的数值。稳定距直接从FLUENT计算结果中得到，大的水舱稳定矩意味着的减摇效果好，水舱阻尼选取适当或者阻尼挡板开度选取适当；小的水舱稳定矩意味着水舱的减摇效果差，水舱阻尼选取不当或者阻尼挡板开度选取不当。根据水舱稳定矩的大小，来定性分析阻尼挡板开度对水舱减摇性能的影响。仿真计算的结果如表2所示。图6所示为阻尼挡板开度与水舱稳定矩曲线图。

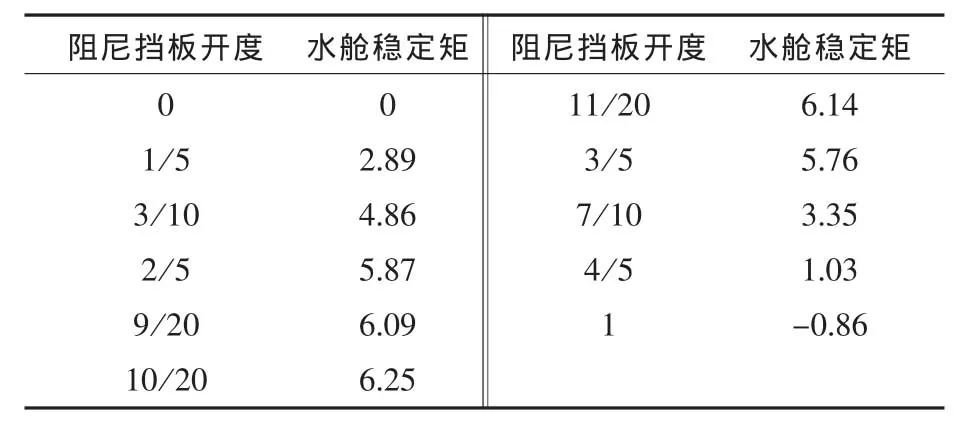
表2 水舱稳定矩的仿真计算结果（N·m）Tab.2 Simulation results of stabilizing moment for the tank （N·m）

4.3 数值仿真结果分析

从定性分析的角度来看，由表2的计算结果可以得出：

1）当阻尼挡板开度为0（即阻尼挡板全闭）时，水舱稳定矩为0 N·m。这是因为阻尼挡板全闭时，舱液几乎不发生振荡运动，舱内的水不会产生减摇力矩。

2）当阻尼挡板开度为0～10／20（即挡板角度为0°～45°）变化的过程中，随着挡板开度的增大，水舱稳定矩逐渐变大，水舱阻尼也逐渐接近水舱最佳阻尼。在阻尼挡板开度为10／20时，水舱稳定矩达到最大，此时的水舱阻尼也即水舱最佳阻尼，水舱的减摇效果最好。

3）当阻尼挡板开度为10／20～1（即挡板角度为45°～90°）变化的过程中，随着挡板开度的增大，水舱稳定矩反而逐渐变小，甚至起到了增摇的作用，水舱减摇效果也越来越差。

4） 当阻尼挡板开度在 2／5～3／5范围内时，水舱有比较满意的减摇效果，说明水舱阻尼选取适当。

台架试验的试验结果认为阻尼挡板在2／5～3／5开度附近时有较好的减摇效果［7］，水舱数值仿真的计算结果与之相比较得到了一致的结论，这也表明了利用数值仿真的方法来研究水舱阻尼是可行的，该数值仿真的结果是合理的。

5 结束语

本文研究了二维减摇水舱中舱液瞬态运动时，不同阻尼挡板开度水舱稳定矩的数值变化，计算得到水舱稳定矩的最大值，找到了水舱的最佳阻尼所对应的水舱阻尼挡板的最佳开度。与台架试验的结果进行比较，得到了与试验结果一致的结论。在进一步定量地进行水舱中舱液的数值仿真研究中，利用FLUENT的UDF功能和动网格计算功能来模拟“船舶－水舱”系统双振荡的整个运动过程，更加全面地研究水舱的舱液运动，更好地实现水舱中舱液流动的数值仿真计算。

［1］李积德.船舶耐波性［M］.哈尔滨：哈尔滨工程大学出版社，2002.

［2］A·H·霍洛季林，A·H·什梅列夫，许百春.船舶的耐波性和在波浪上的稳定措施 ［M］.北京：国防工业出版社，1975.

［3］陶尧森.船舶耐波性［M］.上海：上海交通大学出版社，1985.

［4］赖志昌，王丽慧，金鸿章，等.U型减摇水舱的阻尼研究［J］.船舶工程，2001，23（5）：30－33.

［5］盛振邦，刘应中.船舶原理［M］.上海：上海交通大学出版社，2004.

［6］孙伟.船舶U型减摇水舱控制系统设计及实验研究［D］.哈尔滨：哈尔滨工程大学，2006.

［7］曲加文，张虹，于立君，等.减摇水舱相关参数变化对减摇影响的研究 ［J］.哈尔滨工程大学学报，2004，25（1）：58－61.

［8］王福军.计算流体动力学分析－CFD软件原理和应用［M］.北京：清华大学出版社，2004.

［9］JOHN D.Anderson.Computational Fluid Dynamics—The Basics with Applications［M］.北京：清华大学出版社，2002.

［10］韩占忠，王敬，王小平.Flunet－流体工程仿真计算实例和应用［M］.北京：北京理工大学出版社，2004.

［11］ TZABIRAS G D.A numerical study of turbulent flow around the stern of ship models ［J］.International Journal for Numerical Methods in Fluids，1991，13（9）：1179－1204.

Stabilizing Moment Influenced by Angle of Damping Plate of Anti-Rolling Tank

Jiang Jie1 Ding Yong2
1 China Ship Development and Design Center， Shanghai Division， Shanghai 201108，China
2 School of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China

The damping effect is the important attribute which can influence the stabilizing performance of anti－rolling tank.In a practical design of anti－rolling tank， how to obtain the optimum damping effect has become one of the most critical elements.Improving the damping effect was usually accomplished by changing the cross section of tank＇s channel via the angle adjustment of damping plate.For this purpose，FLUENT was applied to calculate various anti－rolling stabilizing moments based on a 2D numerical model with different angle of damping plate，and reference values of angle which was corresponding with the optimum damping effect in the numerical model were obtained and compared with the results of bench test.The comparison proved the simulation results were reasonable and feasible to research the damping of anti－rolling tank through the FLUENT software.

anti－rolling tank； the angle of plate； FLUENT； numerical simulation

U662.2

A

1673－3185（2011）03－36－04

10.3969/j.issn.1673-3185.2011.03.008

2010-06-18

蒋 颉（1982－），男，助理工程师。研究方向：舰船总体设计。E-mail：jjv9＠hotmail.com

丁 勇（1959－），男，教授，硕士生导师。研究方向：船舶水动力性能。