弧圈球技术集击球稳健性和威胁性于一体的物理分析
2011-03-06唐东阳肖丹丹
唐东阳,肖丹丹
1 前言
弧圈球技术因其稳健性和威胁性的特点,自发明后,迅速风靡世界乒坛[2]。经过几十年的发展,弧圈球已成为当今世界乒坛的主流技术。尽管大多数教练员和运动员对弧圈球的特点有比较清楚的认识,但还有部分教练员和运动员知其然而不知其所以然。本文试图从物理学角度揭示弧圈球具有上述特点的真正原因,以提高教练员和运动员对弧圈球技术的理论认识。
2 弧圈球技术提高击球稳健性的体现及其物理分析
2.1 弧圈球技术提高击球稳健性的体现
击球的稳健性主要包括两点,一是击球要能过网,二是过网后要能落在对方台内。弧圈球技术击球的稳健性是通过制造适宜的弧线来达到的。[3]下面通过物理分析,看弧圈球技术怎样达到提高击球稳健性的效果。
2.2 弧圈球技术提高击球稳健性的物理分析
2.2.1 摩擦使球产生切线方向的平动速度,回球容易过网
在拉弧圈球时,如果摩擦不够,旋转就不够强烈,这一点很容易理解;但另一方面,摩擦不够很容易导致下网。颗粒胶选手很少采用弧圈球技术,主要是由于胶皮的性能,很难制造足够的摩擦,回球容易下网。为什么摩擦不够会导致下网呢?下面来进行物理分析:
拉弧圈球时,一般情况下球拍是前倾的(前倾的角度根据来球的旋转、击球点高度、球拍的性能等不同而不同),在球拍与球接触的瞬间,应给球拍沿拍面方向向前上方加速度。在球拍和球的作用过程中,球受到球拍给予的作用力F。可以把F分解为指向球心的法线方向的力FN和切线方向的力Ff,如图1所示:
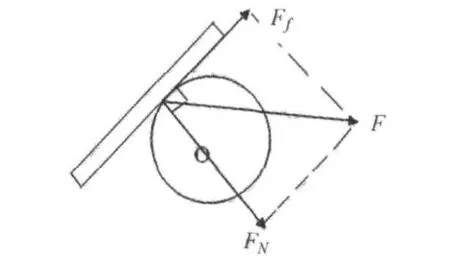
图1 拉弧圈时球拍对乒乓球作用力分解图
FN通过球心O,只能使球产生法线方向的平动加速度和速度,不能使球产生旋转。切线方向的力Ff,也就是我们所说的摩擦力。在大多数文献中,都认为Ff只能使球产生角加速度和角速度。其实,由于乒乓球处于非固定状态,没有固定的转动轴,切线方向的力不但能使其产生角加速度和角速度,还能使其产生沿切线方向的平动加速度和平动速度。[5]正是因为Ff产生的切线方向的斜上方的加速度和速度,才使球能作斜上抛运动,使球更容易过网,达到提高击球稳健性的效果。用弧圈球技术回击比球网低的球时,如果不是Ff产生的沿切线方向的斜上方的加速度和速度,球由于受到的向下的重力作用,在到达网前时肯定比击球点更低,导致直接下网。
2.2.2 球的旋转,会减小出手弧线的打出距离,使击球不容易出台
击球的稳健性既包括击球能过网,还包括过网后能落在对方台内。影响击球是否能落在对方台内的因素很多,如击球的方向、击球的高度、击球时离台的远近、击球的力量、击球的弧线等,其中击球的弧线无疑起着重要的作用。击球弧线的打出距离过短,击球可能不过网,打出距离过长,击球可能落到对方台面的端线以外。那么弧圈球是怎样保证适宜的打出距离呢?
如图2所示:假设在台面高度击球,击出的球没有旋转,做斜抛运动,球离开球拍时的初速度与水平面的夹角为θ,球在飞行过程中只受到重力作用(为讨论方便,本文均不考虑空气阻力和浮力)。
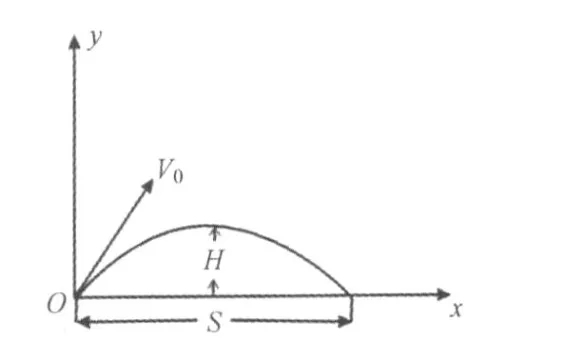
图2 无旋转时乒乓球运动轨迹图
回球飞行弧线的弧高H和打出距离S可用下面公式表示:[1]

由于球网有一定的高度,要想击球过网,飞行弧线必须有足够的弧高。为了保证有足够的弧高H,一方面,可以通过增大初速度V0,另一方面,可以通过调整初速度V0与台面的夹角θ来达到。但随着初速度的增加,打出距离S也会越大,从而有可能导致回球出界。
如果采用弧圈球技术,球在离开球拍后,既有平动初速度V,同时还具有一定的旋转速度ω。图3、图4分别为回球在达到飞行弧线最高点之前和之后的受力图,V为乒乓球的平动速度,ω为乒乓球的旋转速度。
球在到达最高点之前和到达最高点之后,在竖直方向均受到重力G的影响。由于球的旋转,根据流体力学知识,球在飞行的过程中还受到马格纳斯力FM,FM的方向可用右手法则判断:即拇指指向旋转轴(旋转轴方向用右手螺旋法则判断),食指指向球运动方向,中指垂直于手面,其方向就是FM的方向,FM总是与V垂直。因此,在整个飞行过程中,由于球的平动速度的大小和方向不断变化,FM的方向和大小也不停地变化,其大小可用下面公式表示:[6]

图3 到达最高点前的受力图
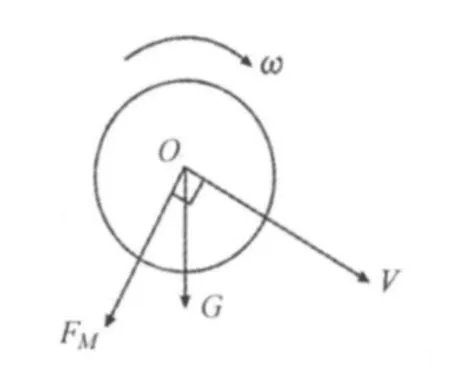
图4 到达最高点后的受力图

其中ρa为空气的密度,d为球的直径。
不管是在图3还是图4中,尽管FM的方向和大小会随着球的运动而改变,但总有竖直向下的分力,正是这个分力,使球产生竖直向下的加速度,使球的向下的加速度在原有的重力加速度基础上增大(没有旋转时向下的加速度仅为重力加速度),导致飞行时间减短,打出距离减短,更好地确保回球落到对方台内。孙在、余广鑫、郭美等(2008)通过计算机仿真模拟也验证,不同的旋转速度对乒乓球飞行弧线的高度和打出距离确实有很大的影响(图5)。
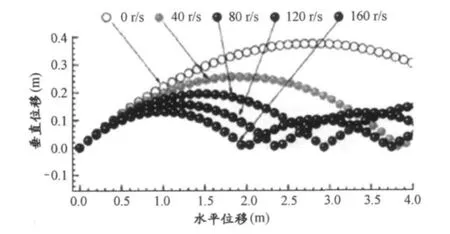
图5 不同旋转速度对弧圈球飞行轨迹影响模拟图(引自《体育科学》,2008,28(4):71)
图5中5条轨迹分别代表平动初速大小、方向相同,但旋转速度分别为0r/s、40r/s、80r/s、120r/s、160r/s的不同回球的飞行轨迹,由于球台长度只有2.74m,从图上可以看出,旋转速度为0r/s、40r/s、80r/s的回球会因为打出距离过长而出台,而旋转速度为120r/s、160r/s就不会打出台。[4]
3 弧圈球技术提高击球威胁性的体现及其物理分析
3.1 弧圈球技术提高击球威胁性的体现
乒乓球运动中击球仅有稳健性是不够的,还必须提高威胁性,才能达到得分的目的。弧圈球技术的威胁性主要通过旋转而影响乒乓球运行的速度、弧线形状、弧线高度、弧线方向以及和球台、球拍作用的效果等,使对方回球出现高球或漏球等失误。下面通过物理分析,看看弧圈球技术是怎么达到提高威胁性的效果的。
3.2 弧圈球技术能提高击球威胁性的物理分析
3.2.1 球的旋转,改变球在飞行过程中的水平平动速度
如果不考虑空气阻力,球在离开球拍后到落到对方台上这段时间,其水平速度是保持不变的,对方容易把握击球节奏。但如利用弧圈球技术,效果就截然不同。根据2. 2.2中的受力分析,乒乓球在离开球拍达到弧线的最高点过程中,因为受到力FM而使球产生一个加速度aM,这个加速度的水平分量aX会导致乒乓球水平方向的速度增大(图6);同样,乒乓球从弧线的最高点到落到对方台面过程中,也因为受到力FM而使球产生一个沿该力的加速度aM,这个加速度的水平分量aX会导致乒乓球水平方向的速度减小(图7)。
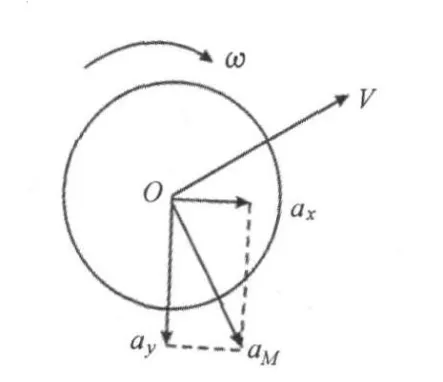
图6 到最高点前球的加速度分解图

图7 到最高点后球的加速度分解图
从上面的分析可以看出,用弧圈球技术击球时球的飞行过程中,前半段水平速度有一个加速的过程,后半段水平速度有一个减速的过程,水平速度突快突慢的变化,一方面,会导致对方对来球节奏判断失误,另一方面,也会使对方对来球的打出距离的判断失误,出现常见的“对不上点”的现象,从而导致失误,达到增大威胁性的效果。
3.2.2 球的旋转,影响球落台时受到的摩擦力,进而影响弹起时的水平平动速度大小
根据动力学知识,乒乓球在落台时和球台的碰撞过程的相互作用和运动可以分竖直方向和水平方向进行研究。

1)在竖直方向上:碰台后的速度VY和碰台前的速度VY0有以下关系:其中e为碰撞恢复系数,由球和球台的材料性质决定,乒乓球和球台的碰撞恢复系数略小于1,因此,在碰台后竖直方向的速度大小改变不多,方向由竖直向下改为竖直向上。
2)在水平方向上:球碰台后的水平速度VX相对碰台前的变化情况取决于球受到的台面给予的摩擦力,而球碰台时和球台之间是否有摩擦力取决于球和台面的接触点相对台面的瞬间水平速度V,V与碰台瞬间球的水平速度VX0以及旋转线速度Vω之间的关系如公式5:如图8:落台前VX0和Vω方向是相反的,Vω方向向左,VX0方向向右,取向右为正方向。

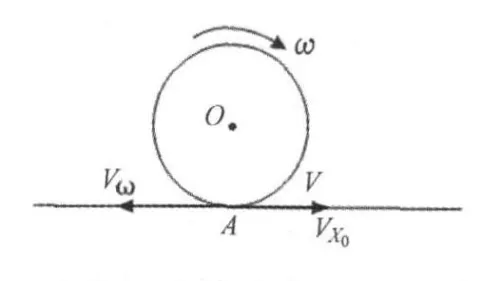
图8 碰台瞬间球和球台接触点的速度图
可分3种情况讨论:
①Vω<VX0时,V为正值,球的碰台点相对于台面的水平速度向右,相对台面向右运动,此时球要受到台面给予的向左的摩擦力f,该力阻碍相对运动,使球产生向左的加速度,使球的水平速度VX减小,导致水平方向的运动速度变慢。实践中,在回接旋转不太强烈的弧圈球时,如果按照旋转强烈的球去回击,由于球落台后往前的速度突然减慢,往往会借不上力,原因就在这里。有经验的运动员在使用弧圈球技术时,并不一定每一板都拉出强烈的旋转来,而是偶尔会拉出一板旋转并不很强的所谓“假弧圈球”来,这时反而会起到意想不到的效果。
②Vω=VX0时,V=0,球的碰台点相对于台面的水平速度为0,因此,球不受台面的摩擦力,碰台后球的水平速度VX几乎不改变。
③Vω>VX0时,V为负值,球的碰台点相对于台面的水平速度向左,此时球要受到台面给予的向右的摩擦力f,该力也阻碍相对运动,使球产生向右的加速度,使球的水平速度VX增大,导致水平方向的运动速度变快。实践中,回接旋转强烈的弧圈球,往往会出现“球顶拍”、发不出力的情况,这正是因为旋转强烈的弧圈球落台后水平速度突然加快,导致对方引拍不够、挥拍距离过短的原因。
3.2.3 球的旋转,影响球落台时受到的摩擦力,进而影响弹起时的平动速度方向
如3.2.2中分析,当Vω<VX0时,球要受到台面给予的向左的摩擦力f的影响,f使球的水平速度VX减小,而竖直方向的速度大小几乎不变,因此,总的平动速度减小,这会导致反射角小于入射角,球的弹起线路比没有旋转的球要高;当Vω>VX0时,此时球要受到台面给予的向右的摩擦力f,f使球的水平速度VX增大,而竖直方向的速度大小几乎不变,会导致反射角大于入射角,球的弹起线路比没有旋转或旋转不强烈的球要低,给人以球突然下坠的感觉,回击时容易造成“漏球”现象。实践中,在连续拉出旋转强烈的弧圈球后突然拉出一板不转或旋转很弱的“假弧圈球”,就会给人以球落台后突然“上拱”的感觉,使对方回球失误。
3.2.4 球的旋转,会压低球的飞行弧线和弹起弧线
球落台后弹起弧线越低,给对方的威胁越大,对方进攻的难度也越大;弹起弧线越高,给对方的威胁性也就越小,对方进攻也就越容易。但为了保证回球能顺利过网,飞行弧线必须有一定的高度。对于没有旋转的球,飞行弧线越高,就会导致落台后的弹起弧线也高。弧圈球能使较好地解决这个问题,如2.2.2中分析,弧圈球由于具有旋转速度,不论是在出手弧线还是弹起弧线过程中,球一直会受到一个马格纳斯力FM,FM总有一个竖直向下的分力,从而起到压低弧线的作用。在拉弧圈球时,为了保证球能过网,我们不得不使球在过网前有较高的弧线,但过网后,由于具有旋转速度,受到的马格纳斯力FM会压低弧线,确保弹起弧线不至于太高。另一方面,球落台后还具有一定的旋转速度,会继续受到马格纳斯力的作用,这个力继续起到压低弹起弧线FM的作用。在实践中,我们发现,旋转强烈的弧圈球落台后弹起弧线特别低,除了3.2. 3中所提到的原因外,这也是一个重要原因。
3.2.5 球的旋转,会改变球和对方球拍之间的摩擦力,进而改变对方回球后的飞行线路
球在弹起后被对方回击时,球和对方球拍之间的摩擦,会改变球离开球拍后的飞行线路。由于球拍和球之间的摩擦系数远大于球台和球之间的摩擦系数,因此,球拍对旋转的乒乓球产生的摩擦力较大,对乒乓球平动速度的大小和方向改变更为明显。当球与球拍作用时,如果Vω<V11,其受到的摩擦力如图9所示,此时球受到的摩擦力会使沿接触点切线方向的平动速度减小,反射角小于入射角,球的弹起线路较低;如果Vω>V11时,其受到的摩擦力如图10所示,此时球受到的摩擦力会使沿接触点切线方向的平动速度增大,反射角大于入射角,球的弹起线路较高。在实践中,如果拍形调节不好,回接旋转强烈的球,容易出现高球或出台;如果回接旋转不太强烈或不转的球,容易下网,原因就在这里。
3.2.6 借助球的旋转,把球拍传递给球的动能部分转化为球的转动动能,从而增大球的总动能
击出球的动能越大,给对方的威胁也越大。对于没有旋转的回球,其动能的大小E=1/2MV2,乒乓球的质量是固定的,要增大动能,就只能增加平动速度。在2.2.2中已经指出,平动速度过大,容易导致打出距离过大而出台。弧圈球技术就很好地解决了这一问题,通过把球拍传递给球的动能部分转化为球的旋转动能,一方面,不因平动速度过大而导致出台,达到确保回球的稳健性的效果,另一方面,又使球具有足够大的动能,在落到对方台面和撞击对方球拍时通过摩擦力的作用表现出来,给对方回球制造困难,达到确保回球的威胁性的效果。
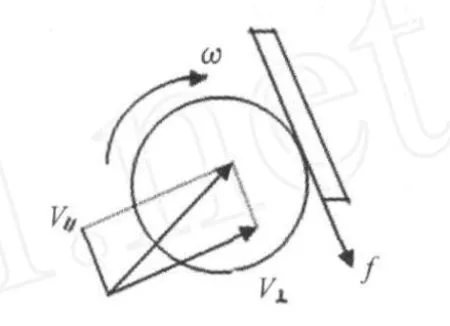
图9 Vω<V11时球拍对球摩擦力方向图
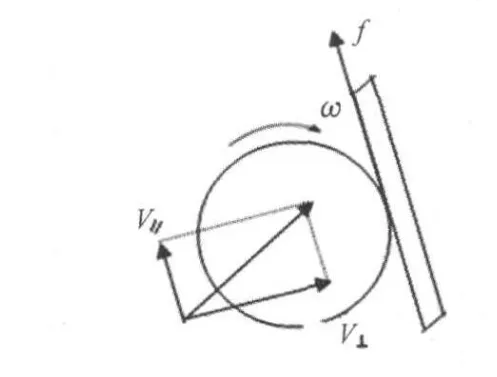
图10 Vω>V11时球拍对球摩擦力方向图
3.2.7 球的侧旋,改变飞行弧线和弹起弧线的方向
乒乓球可以绕任一条直径旋转,但不管以哪条轴为旋转轴的旋转,都可以把它看成分别绕冠状轴(左右轴)、矢状轴(前后轴)、垂直轴(上下轴)三种旋转的合成。前冲弧圈球和高吊弧圈球只绕冠状轴(又称额状轴)旋转。此外,还可以拉出侧旋弧圈球,这种弧圈球的旋转是由绕冠状轴的旋转和绕矢状轴的旋转合成。绕冠状轴的旋转的作用和效果如前面我们所讨论的一样。绕矢状轴的旋转可以使球在飞行过程中,也要受到马格纳斯力FM的作用,不过根据右手法则判断,FM的方向在水平面上,会引起球的运行方向的改变,使球向外拐(类似足球中的“香蕉球”)。同样,在碰台过程中,也会产生摩擦力,改变球的弹起弧线的方向,使球向外拐。正是这种外拐,增大了对方回球的难度,从而达到增大威胁性的效果。
4 小结
弧圈球技术集回球稳健性和威胁性于一体的特点已被乒乓球界广泛认识。其稳健性和威胁性主要是通过以下途径实现的:
1.摩擦使球产生切线方向的平动速度,确保回球过网。
2.减小出手弧线的打出距离。
3.改变球在飞行过程中的水平平动速度
4.影响弹起时的水平平动速度大小。
5.影响弹起时的平动速度方向。
6.压低飞行弧线和弹起弧线。
7.改变对方回球后的飞行线路。
8.把球拍传递给球的部分动能转化为球的转动动能,从而增大球的总动能。
9.球的侧旋,改变飞行弧线和弹起弧线的方向。
限于目前实验条件的不足,本文仅从物理学角度定性分析弧圈球具有稳健性和威胁性的原因,未能进一步用实验进行定性研究和验证,这是本文的不足之处,也将是下一步的研究方向。
[1]程守洙,江之永.普通物理学[M].北京:高等教育出版社,1998. [2]邱钟惠,庄家富,孙梅英,等.现代乒乓球技术的研究[M].北京:人民体育出版社,1982.138.
[3]孙在,余广鑫,郭美,等.乒乓球弧圈球的空气动力学原理及其飞行轨迹的仿真分析[J].体育科学,2008,28(4):69-71.
[4]唐东阳,陈乔龙.乒乓球与球拍之间的摩擦[J].武汉体育学院学报,2007,41(7):56-58.
[5]徐文熙,徐文灿.粘性流体力学[M].北京:北京理工大学出版社,1989.
