对于田径径赛场地占地面积的研究

纪和江

1 研究意义

田径场地文化是田径运动文化的一脉,内涵丰富。纵观田径运动场地的发展史,不仅饱含着社会物质文明的进步,也表达着人们精神领域的追求。其中场地类型与占地面积之间的关系、场地半径与占地面积之间的关系是场地文化中的一域。场地周长相同、跑道宽度相同,场地类型不同、场地半径不同,占地面积存在着明显的差异。揭示这一现象,对于节省土地面积、科学合理地布局场地、因地制宜地修建场地、提高土地的使用效率、完善相关土地使用政策以及对于场地建设的评价体系都有着重要的意义。

2 研究内容

2.1 圆形、矩形周长面积率

周长面积率就是周长与面积之间的比值关系,或称面积产长率。创新这一数学公式表达法,不需计算就可直观准确表达不同半径的圆形、不同长宽的矩形,周长与内含面积之间的关系。

2.2 半圆式场地周长之比与占地面积之比

常见的半圆式场地有周长400 m和周长300 m、200 m的小型场地,不同场地间在周长之比与半径之比等值的前提条件下,占地面积之比存在着内在规律。

2.3 半圆式场地周长相同、半径不同占地面积的差异

场地占地面积不仅决定于场地周长,还决定于场地的半径。在场地周长相同、跑道宽度相同、半径不同的情况下,不同半径之间的场地占地面积存在差异。

2.4 双曲率场地与半圆式场地占地面积的比较

双曲率场地多见于欧洲的某些国家,国际田联《场地设施标准手册》在规定周长400 m、半径36.5 m的半圆式场地为标准场地的同时,也列举了3种双曲率场地,这也充分说明了这种场地的存在意义。场地的占地面积取决于多种因素,半圆式场地与双曲率场地的横轴宽度相同、场地周长相同,两者间占地面积是否相同,差异如何?

3 研究结果

3.1 圆形、矩形周长面积率的公式、与图形表达

半圆式径赛场地是由两端对称的两个半圆和两个半圆之间的矩形构成的平面几何图形。通过揭示圆形、矩形周长与面积之间的关系,就可明晰场地半径与占地面积之间的关系。

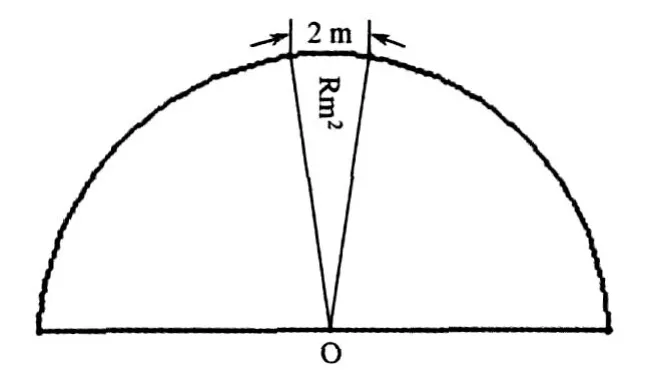
图1 圆形周长面积率说明图

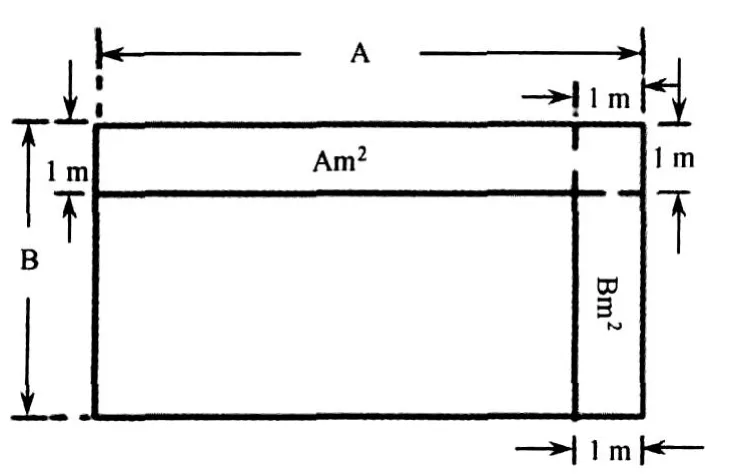
图2 矩形周长面积率说明图

3.1.1 圆形周长面积率

通过简单的数学公式推导,可分别得到圆形周长面积率与矩形周长面积率。

注：L=周长；S=面积；R=半径；N=圆形周长与面积比。

3.1.2 矩形周长面积率

注：B=矩形短边；A=矩形长边；N=矩形周长与面积比。

圆形、矩形周长面积率,直观、简捷地表达了半圆式场地半径、周长与占地面积之间的关系。

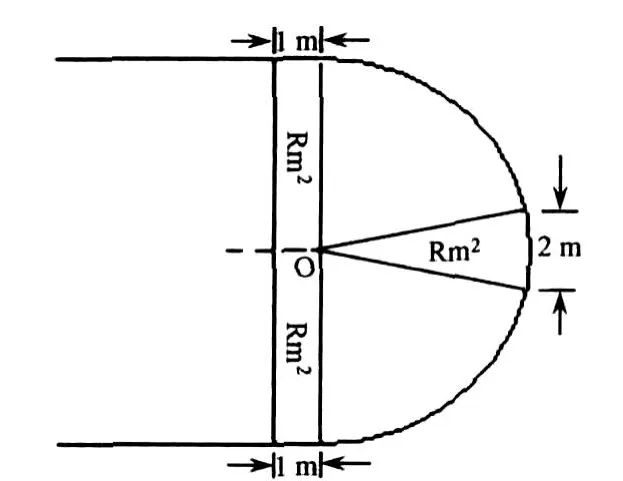
图3 半圆式场地半径与面积率说明图

3.2 不同周长的半圆式场地占地面积的比较

3.2.1 圆形、矩形周长与占地面积

圆形的半径分别为18 m、27 m、36 m,其半径比、周长比、面积比如下：

半径比：1∶1.5∶2；周长比：1∶1.5∶2；其面积比为半径比(或周长比）的平方,面积比：1∶1.52：22即 1∶2.25∶4。

矩形边长分别为：A1=42 m、B1=18 m,A2=63 m、B2=27 m,A3=84 m、B3=36 m；

周长比：1∶1.5∶2；A边比：1∶1.5∶2；B边比：1∶1.5∶2；其面积比为周长比(或A边比或B边比）的平方,面积比：1∶1.52∶22即1∶2.25∶4。

图4 场地平面结构说明图

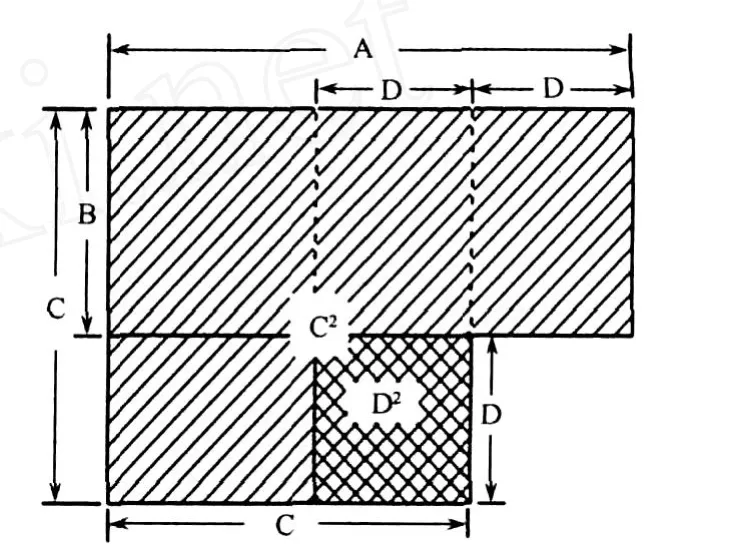
图5 矩形长宽比与面积说明图

3.2.2 对于周长400 m、300 m、200 m场地占地面积的比较

由于田径场地对于跑道计算以及周长表述的特殊性,场地各种数据间的关系既遵循上述圆形、矩形周长与内含面积的一般规律又有其特殊性。以场地设内突沿,场地周长的计算线距内突沿外沿0.30 m计算,对于周长400 m、300 m、200 m,跑道宽度均为1.226=7.32(m）的3种场地,内场及全场占地面积比较如下：

3.3 相同周长不同半径的半圆式场地占地面积的比较

3.3.1 相同周长、不同长宽比例的矩形占地面积比较

矩形的周长相同、长宽比例不同占地面积不同,长宽比例差异越大,占地面积差异越大。

为了直观地表达相同周长的矩形长与宽的比例不同,导致占地面积的差异,采用第二种矩形周长面积率的公式表达法。

注：A=矩形长边；B=矩形短边；C=(A-D）=(B+ D）；D=(A-B）/2。

在矩形周长相同的前提条件下,A与B的差值越大,D值就越大,N值也越大,产长率也就越高。D值越趋于零,矩形就越趋于正方形,N值就越小,正方形(D值为零）产长率最低。

3.3.2 相同周长、不同半径的半圆式场地之间占地面积的差异

场地半径不仅决定圆区的占地面积,也决定矩形区的占地面积,根据圆形、矩形周长面积率：场地半径越小,曲段的产长率越大,直段的产长率也越大。但是,对于半圆式场地而言,曲段的产长率是直段产长率的2倍,在周长相同的条件下场地半径越小,直段长度就越大,这对于占地面积的影响如何?

不同半径、相同跑道宽度的半圆式300 m场地之间占地面积的比较；不同半径、相同跑道宽度的半圆式200 m场地之间占地面积的比较。

表2所示,周长相同的场地,跑道宽度也相同,半径差异不仅决定了圆区周长面积率的差异,也决定了矩形区周长面积率的差异。尽管场地半径越小,两侧直段长度越大,不同半径的场地之间占地面积仍然存在着明显的差异。

表1 不同周长半圆式场地占地面积比较一览表

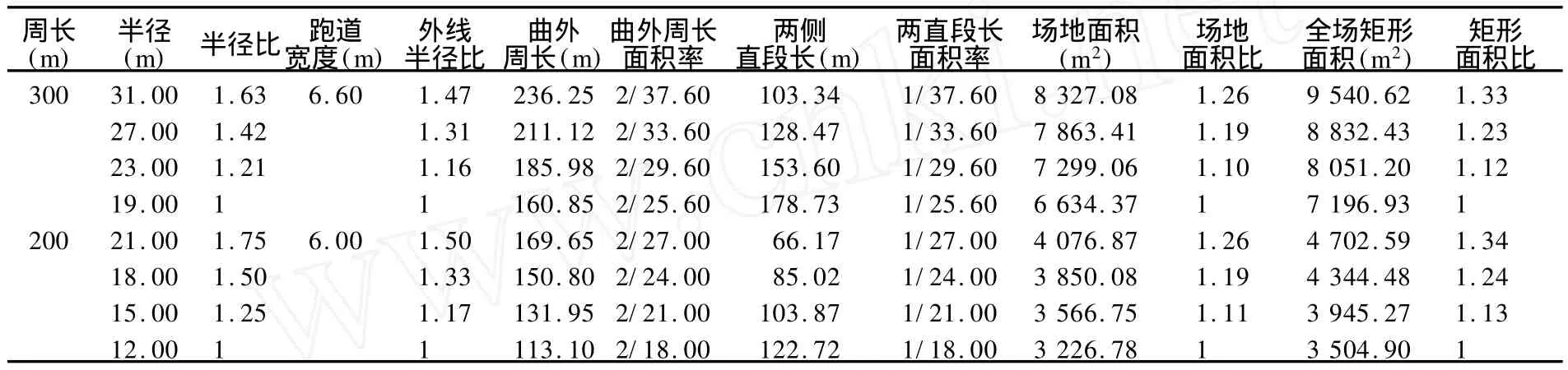
表2 周长300 m、200 m半圆式场地占地面积比较一览表

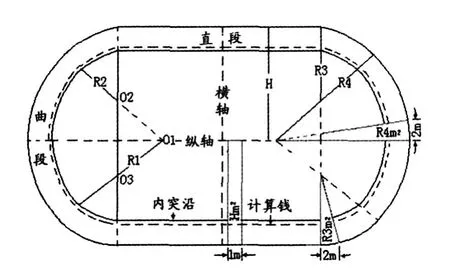
图6 双曲率场地示意图

同为周长300 m,跑道宽度同为6.60 m,半径19 m的场地,比半径31 m的场地少占地1 692.71 m2；比半径27 m的场地少占地1 229.04 m2；比半径23 m的场地少占地664.69 m2。半径19 m场地的全场矩形面积,比半径31 m的场地少占地2 343.69 m2；比半径27 m的场地少占地1 635.50 m2；比半径23 m的场地少占地854.27 m2。

3.4 半圆式场地与双曲率场地占地面积的比较

国际田径联合会《场地设施标准手册》列举的3种双曲率400 m场地分别是德国式、法国式、瑞典式的,尽管它们之间在其平面结构的数据上也有差异,但其共同点是场地的曲段突沿为2种不等半径的弧连接而成,故称双曲率。

3.4.1 双曲率场地的平面结构

半圆式场地与双曲率场地的平面结构比较,二者的差别在于：半圆式场地每侧曲段(半圆部分）只有1个圆心,内场圆区与曲段的各条分道都分别为等半径弧；双曲率场地每一侧的曲段分别由1个大半径弧和2个相同长度的小半径弧组成的,即每侧曲段有3个圆心。除此之外二者的平面结构概貌大致相同。

3.4.2 双曲率场地与半圆式场地占地面积的比较

双曲率场地与半圆式场地相比：在周长相同,横轴宽度相同,跑道宽度相同的前提条件下,分析其占地面积的差异,可直观地得到如下结论：R3为小半径的扇形区(R2+跑道宽）周长面积率值要明显大,R4为大半径的扇形区(R1+跑道宽）周长面积率值要明显小。但是,由O1、O2、O3构成的三角形为直段与曲段的共享区,如果约定此三角形构成的区域计算在矩形区的面积产长率之内,那么,在横轴宽度相同的情况下2类场地矩形区域“对边之和面积率”是相等的,曲段的面积产长率,双曲率场地要明显的大于半圆式场地。

表3 半圆式场地与双曲率场地占地面积比较一览表

对表3的数字分析可以得到如下结论：同样周长、同样横轴宽度的两类场地,由于类型差异,场地整体与构成场地整体的各个部分占地面积不同,甚至差异较大。双曲率场地内场矩形区面积最大,全场矩形区占地面积最小,在保证了内场矩形区域和跑道区域使用面积的前提条件下,有效地减少了场地的闲置面积。

两类周长400 m的场地,双曲率比半圆式内场矩形区面积大约905 m2；全场矩形面积区小约458 m2；两类周长300 m的场地,双曲率比半圆式内场矩形区面积大约509 m2；全场矩形区面积小约253 m2；两类周长200 m的场地,双曲率比半圆式内场矩形区面积大约226 m2；全场矩形区面积小约120 m2。

4 结论与建议

4.1 结论

4.1.1 关于圆形、矩形周长面积率

圆形、矩形周长面积率可以准确表达圆形周长、矩形周长与占地面积之间的关系,为直观地判断田径场地半径、周长与占地面积之间的关系提供了简捷的理论依据。

4.1.2 不同周长半圆式场地占地面积的基本规律

不同的圆形之间：半径比为1∶2；周长比为1∶2；面积比为1∶4。不同的矩形之间：长边比为1∶2；短边比为1∶2；周长比为1∶2；面积比为1∶4。田径场地具有计算与表述的特殊性,但也遵循其基本规律。

4.1.3 相同周长不同半径的半圆式场地占地面积的基本规律

半圆式场地周长相同,半径越小占地面积也越小,半径不仅决定了圆区的面积产长率,也决定了矩形区域的面积产长率。

4.1.4 双曲率场地占地面积的特点

双曲率场地与半圆式场地在周长相同、横轴宽度相同的前提条件下,双曲率场地的内场矩形区面积最大,而场地面积(内场面积区与跑道区之和）与全场矩形区面积最小。

4.2 建议

4.2.1 对于田径场地建设的思考

除了以竞技为主要用途的场地应按国际田联《场地设施标准手册》规定的标准田径场地建造外,其他田径场地的建造都应遵循“满足功能”、“节约用地”、“综合利用”这三项基本原则。

4.2.2 对学校体育场地评估、验收的建议

在对学校体育场地的建设、评估、验收中,目前往往用学生人均占地面积指标衡量是否达标。通过对于田径场地跑道周长、类型、半径与占地面积之间关系的解读,对于利用跑道周长来说,面积却不能够准确表达功能。增设对于土地的使用效率的评估,对于充分利用土地,优化各类场地的总体布局,会起到颇有意义的导向作用。

4.2.3 应推广双曲率的小型田径场地

双曲率场地多见于欧洲一些国家,在我国无论是周长400 m的场地,还是其他规格的小型场地,很可能就没有这种类型的场地。无论从节约土地面积,还是从对其他项目场地的综合布局思考,在寸土寸金的今天合理用地、科学布局场地,都是利国利民尤为重要的有益之举。

对于各级、各类学校来说,解读场地类型、半径与占地面积之间的关系,从实际出发因地制宜地修建场地就显得更有实用价值。

为什么双曲率场地未能在我国普及,主要原因有两点：一是,没有全面深刻解读这种场地的文化内涵,换言之,我们并没有告知人们一个同样周长、同样功能的双曲率场地比半圆式场地能够节省多少土地面积；二是,双曲率场地跑道计算较为复杂(划线操作并不复杂）,又无有据可查的设计与划线指导依据,更无广大基层可套用的设计范例和具体数据。因此,欲想普及这种场地,就必须首先告知人们这种场地的优点,必须解决场地设计与划线数据相关的技术问题。

[1]国际田径联合会地区发展中心.国际田联田径设施手册[M].北京：北京体育大学出版社,2006：1-22.

[2]体育院、系教材编审委员会《田径》编写组.体育系通用教材.田径[M].北京：人民体育出版社,1985：132-212.

[3]中国田径协会译审.国际田径协会联合会田径场地设施标准手册[M].北京：人民体育出版社,2003：3-4.

[4]中国田径协会审定.田径竞赛规则[M].北京：人民体育出版社, 2006.