反J-C模型调控纠缠原子量子特性
2011-03-03吕东燕周原
吕东燕,周原
(湖北汽车工业学院,湖北 十堰 442002)
反J-C模型调控纠缠原子量子特性
吕东燕,周原
(湖北汽车工业学院,湖北 十堰 442002)
单个二能级原子在强经典驱动和大失谐的双重条件下,系统可以等效化为反J-C模型。在此模型中将一对纠缠二能级原子中的一个注入该腔中,演化之后,对腔外原子做选择性测量,可以调控腔内原子的布居和偶极压缩。经过研究发现利用此种方法来远程调控原子的布居和偶极压缩效果更佳。
量子光学;纠缠;布居;偶极压缩
光场与原子的量子特性一直是量子光学方向的主要研究内容[1-5],利用纠缠关联来远程操纵原子的性质已经取得了一些研究进展,研究此类问题通常是采用腔QED理论。以前研究所采用的模型如J-C模型、T-C模型都是理论中的理想条件下的标准模型,当考虑到实际实验的时候这些模型就太理想化了[6-10]。有理论研究发现,在单个二能级原子注入腔中,在强驱动场的作用下与光场发生相互作用,在大失谐时发现系统的有效哈密顿量为标准的J-C模型或反J-C模型。由于J-C模型已经研究的很全面也很充分,所以在这个思路的指引下以反J-C模型为研究主体,利用这个模型来研究远程调控原子的量子特性[11-13]。
1 基本模型
考虑单个二能级原子在经典的驱动场的作用下与腔内的光场发生相互作用,取ħ=1,系统的哈密顿量可以写为
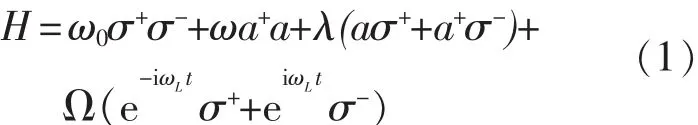
式中:ω0—原子的跃迁频率;ω—光场的频率;ωL—经典驱动场的频率;a+,a—光场的产生和湮灭算符;

考虑开始时腔内的光场为相干态光场,那么系统的初态为
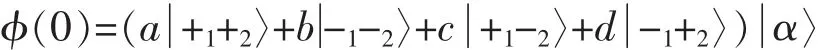
求解薛定谔方程可得,在相互作用绘景下,系统在任意时刻的波函数为


式中:N—归一化系数。
2 数值计算和分析
2.1 调控原子的布居

则在相互作用绘景下可以得到Sz的期待值为
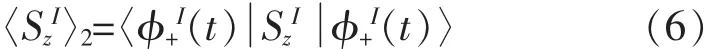
可以得到原子2在腔内的布居分布。
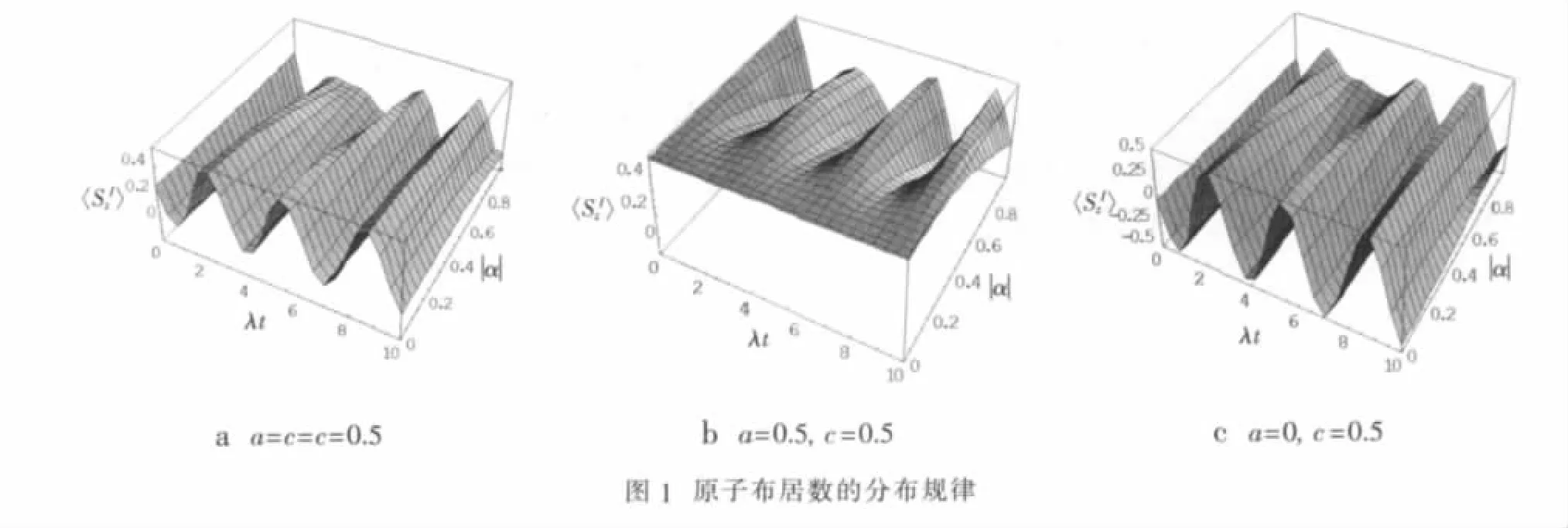
由图1可以看出在选择不同初态的情况下,原子2的布居数分布会呈现不同的变化规律。初态选的不同,原子布居数变化的范围也不相同,尤其是布居数正负值的差别比较大。另外布居数的变化也会受到时间、耦合参数、相干态光场的参数的调制,时间和耦合参数的影响主要是会形成周期性的震荡,而参数的调制主要体现在一些局部区域,如图1a~c所示。
2.2 调控原子的偶极压缩
定义2个相互正交的算符

Fi<0表示原子存在偶极压缩,反之则没有偶极压缩。不失一般性只选取F1作数值分析。
根据图2可以看到,原子2有很明显的压缩现象发生,并且压缩区域的大小可以受时间、耦合参数、外驱动场频率的调制,可以实现原子2稳定的偶极压缩如图1b~d所示。时间和外驱动场频率对偶极压缩还会产生周期性的调制,实现偶极压缩的周期性震荡,如图1a所示。另外在数值分析时,发现初始量子态的选取(a,c的取值)、相干态光场的参数α中,x,y的选取对原子2的偶极压缩的强度也存在制约,可以通过选择合适的初态或相干态光场来改变原子偶极压缩的强弱。

3 结论
在量子光学和量子信息研究领域中,制定一些可控的方案用来改变原量子系统的许多量子特性是一个重要研究课题。本文的研究结果表明利用原子间的纠缠关联,通过选取合适的激光场(相干态),有针对性的调节光场与原子之间相互作用的条件,来控制改变纠缠的腔内原子的量子特性,经过理论分析和数值计算发现可控性比J-C模型更好。
[1]彭金生,李高翔.近代量子光学导论[M].北京:科学出版社,1996:156-198.
[2]Walls D F,Zoller P.Reduced Quantum Fluctuations in Resonance Fluorescence [J].Phys.Rev.Lett.,1981, 47:709-711.
[3]刘堂昆,王继锁,等.纠缠态原子与相干光场作用的量子信息保真度[J].光学学报,2000,20:1449-1455.
[4]Sanders B C.Entangled coherent states.[J].Phys.Rev.A,1992,45:6811-6815.
[5]郑小虎.双模纠缠相干光场与V型三能级原子相互作用系统的光子统计性质 [J].原子与分子物理学报, 2005,22:325-331.
[6]Yang C P,Guo G C.Controllable emission properties of an atom inside a cavity by manipulating the atom outside the cavity.[J].Phys Lett A,1999,255:129-132.
[7]杨雄,向少华,宋克慧.双光子Jaynes-Cummings模型中的纠缠演化和热纠缠态现象[J].原子与分子物理学报, 2004,21:68-72.
[8]罗玉,李莹,潘庆,等.利用谐振倍频产生纠缠光束[J].光学学报,2006,26:305-310.
[9]徐大海,彭金生.高Q克尔介质腔中依赖强度耦合的JC模型中光场相位特性[J].光学学报,2000,20:56-61.
[10]Xia Y J,Guo G C.Squeezing and Entanglement in Continuous Variable Systems[J].Chin.Phys.Lett., 2004,21:1877-1880.
[11]周原,张英杰,夏云杰.远程控制光场的量子统计性质[J].光学学报,2007,06:1122-1128.
[12]杜秀梅,夏云杰,周原.非简并k光子J-C模型中光场的量子统计特性[J].量子电子学报,2008,25(5):598-604.
[13]张英杰,夏云杰,任廷琦等.反Jaynes-Cummings模型下纠缠相干光场量子特性的研究[J].物理学报,2009, 8(2):722-728.
Control of Quantum Properties of Entanglement Atom with Anti-J-C Model
Lü Dongyan,Zhou Yuan
(Hubei Automotive Industries Institute,Shiyan 442002,China)
A two energy level atom can be converted into anti-J-C model equivalently under the condition of strong driven classical field and large detuning.One of the couple of entangled two-level atoms is poured into the cavity in this model.After the evolution,the atom out of the cavity is selectively measured,the occupancy and the dipole squeezing of the atom in the cavity can be controlled.It is found that the result is better in this way for controlling the occupancy and the dipole squeezing of the atom remotely.
quantum optics;entanglement;occupancy;dipole squeezing
O431.2
A
1008-5483(2010)01-0065-03
2011-01-28
湖北汽车工学院科技学院青年创新基金资助
吕东燕(1980-),女,山东济宁人,硕士,主要从事相变与临界现象、BEC、量子学等方面的研究。
