基于灰熵方法的学生综合评价问题
2011-02-28余瑞艳
余瑞艳
(长江大学一年级教学工作部,湖北 荆州434020)
1 引 言
综合评价是一个典型的多目标决策问题,在用灰色关联进行分析的过程中,灰色关联度的计算实际上是将各项指标等权划分,这样会因为没有考虑到各指标重要性差异和允许指标属性之间可以相互线性补偿,且被补偿的值不受任何限制而导致存在信息流失、误差大等缺陷,而采用主观赋权法又无法消除各因素权重的主观性[1].引入信息熵的概念,通过其反映评价指标信息的效用值来映射权重,这可以避免权重计算的主观性,使评价结果更客观、符合实际,为学生综合评价提供一种新方法[2].因此,算法采用基于灰色关联度的灰色综合评价决策模型,运用熵来确定指标权重.于是利用基于熵原理的灰色关联分析方法,确定了在学业测评模式和综合测评模式下各班的优劣情况.很多文献已经讨论了如何进行合理的席位分配[2-5],但还没有相关文献如何进行奖学金分配才是最合理的,于是基于以上思想,本文提出了一类基于不同决策者偏好系数β∈[0,1]的评价函数f,确定了基于综合测评模式的奖学金分配原则是较合理的,并在文章的最后对以上模型提出了改进方法,使得问题的分析更有合理、有效.
2 算法原理
灰色关联分析把各项指标等权划分,无法给出各评价指标的重要性差异,而按照信息论观点,各个指标在指标体系中的作用,与指标的变异度有关,指标的变异度越大,它所携带和传递的决策信息越多,对方案的比较作用也越大.信息量的大小可用熵值来测度,熵值的减少意味着信息量的增加.熵值法根据各指标的信息载量的大小来确定指标权重.熵值法的最大优点是其计算得到的权重完全是依据属性矩阵所带的信息,没有任何主观判断,能够得出较为客观的综合评价结果[1,6].
2.1 指标规范化处理
设原始指标属性矩阵D=(Zij)m×n,则对效益型指标规范化处理,有:
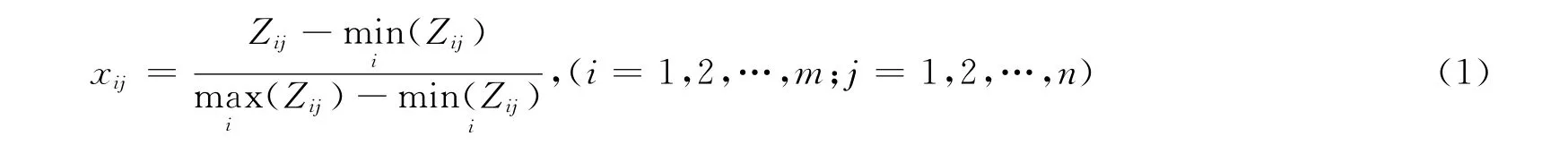
对成本型指标规范化处理,有:
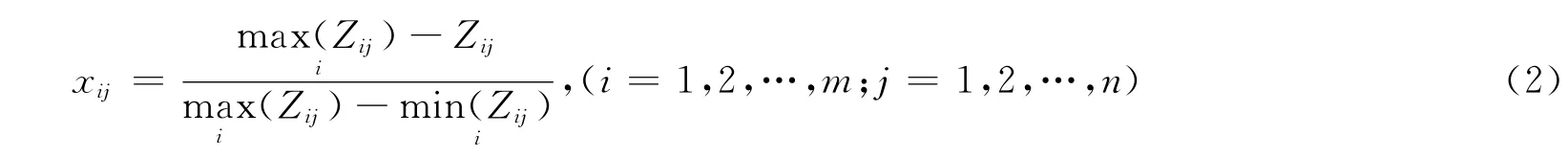
2.2 各指标灰色关联系数的计算
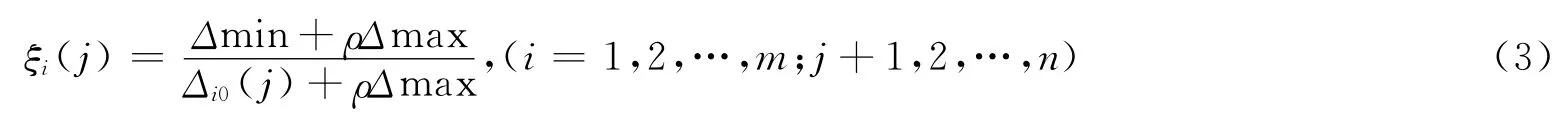
式中Δmin=min min{|x0(j)-xi(j)|},Δmax= max max{|x0(j)-xi(j)|}分别为比较序列绝对
ijij差中的最小值和最大值,Δi0(j)=|x0(j)-xi(j)|为比较序列的绝对差,ρ为分辨系数,取值范围为ρ∈(0,1),通常取ρ=0.5.
2.3 熵值法计算权重的步骤
(1)设原始指标属性矩阵D=(Zij)m×n,其中Zij为第方案在第指标下的指标属性值,则第i个方案对第j个指标属性的贡献度Pij为:
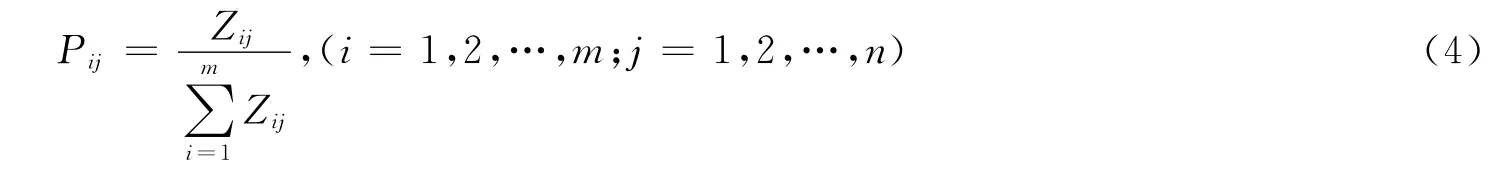
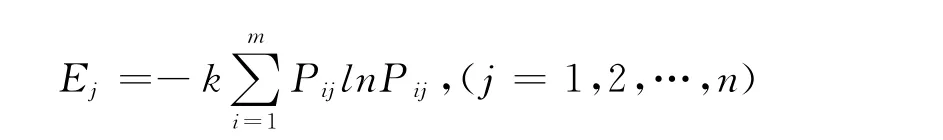
其中取k=1/(ln m),k>0,Ej∈ [0,1],且设Pij=0时,Pijln Pij=0.
(3)定义第j个指标下各方案贡献度的差异系数,其计算公式为:gj=1-Ej,(j=1,2,…,n),则当gj越大时,指标越重要.
(4)将其指标权重归一化就得到各评价指标的权重,其计算公式[8]为:
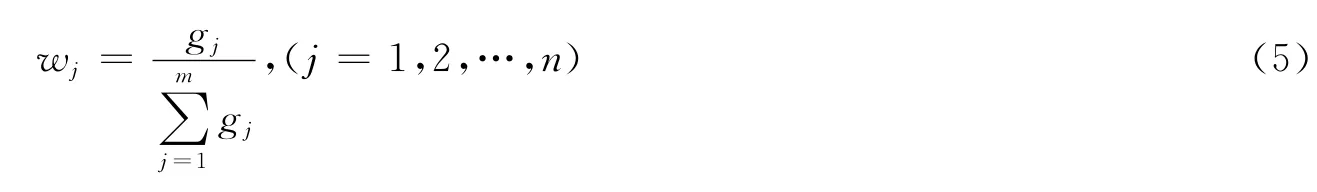
(2)对于此贡献度所包含的信息内容,可以用熵Ej来表示,所有方案对第j个指标的贡献总量,计算公式为:
2.4 计算综合评价值
3 算例分析
3.1 班级排序
影响班级优劣情况很多,结合每个班级的事情情况,针对以学业表现为基础的测评,取主要的评价指标有7个:优秀率、良好率、中等率、及格率、不及格率、人均补考或重修率;而针对综合测评,取除人均补考或重修率之外的其它6个指标.具体数据见表1
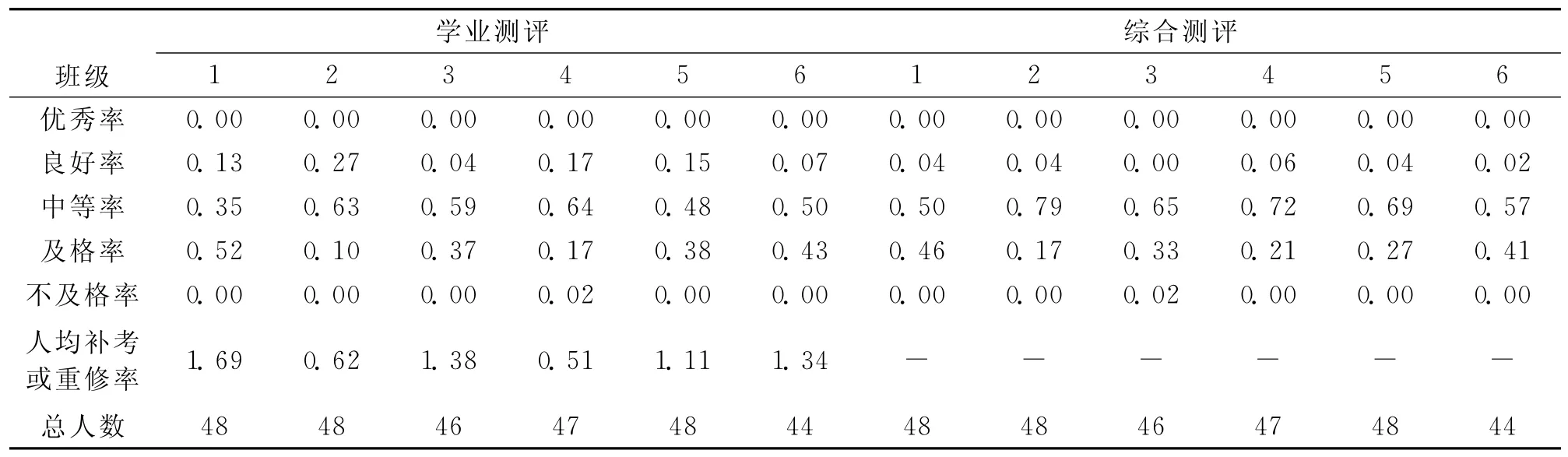
表1 各班学业表现和综合测评情况
根据实际情况,取指标优秀率、良好率、中等率为效益型指标,而及格率、不及格率、人均补考或重修率为成本型指标,根据灰色关联系数的计算步骤对表1中数据进行规范化处理后得到在学业表现测评和综合测评下的灰色关联系数矩阵分别为:

由表中数据,根据熵值法计算权重的步骤得到各指标的权重为:
w1j= {0.0000,0.2407,0.1633,0.2411,0.1291,0.2257}
w2j= {0.0000,0.2363,0.2701,0.3101,0.1836}
用计算综合评价值的公式计算得到各方案的综合评价值为:
D1i= {0.2233,0.9733,0.4097,0.7260,0.5088,0.3636}
D2i= {0.3411,0.9212,0.2787,0.8920,0.7212,0.3810}
根据计算得到的综合评价值,得到在学业表现和综合测评下各班的优劣顺序如表2所示:

表2 不同测评模式下各班的优劣排序情况
3.2 奖学金分配
在上一算例的分析中,借用基于熵原理的灰色关联分析方法确定了各班在不同测评模式下的优劣情况,但没有相关文献比较过这两测评模式之间的优劣程度.该问题提出了一在两种不同测评模式下的奖学金分配原则,即每班按照5%的比例确定人选,最后取的总人数不足或超过规定人数时,采取把相关人员不同测评模式下的成绩作比较.迄今还未有相关文献对采用哪种分配方式更合理作出科学有效的解释,基于此,笔者提出了一类基于不同决策者偏好系数β∈[0,1]的评价函数f.

表3 基于相同分配原则的各班奖学金分配情况
在不同测评模式下笔者已求出了各班与最优理想班级的灰色关联系数,如果关联系数越大则表示该班离最优班的距离越小,基于该思想,认为在名额的分配过程中,如果最终总的加权灰色关系数越大则表示该中分配方案越合理、有效[7-9].
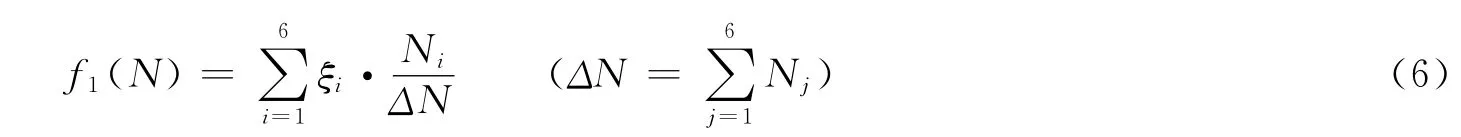
其中ξi表示第i班的关联系数,Ni表示第i班获得奖学金的人数,则函数f1(N)越大越能体现公平性,体现在奖学金的分配方面就是:如果第i班的灰色关联系数越大,则该班所得的奖学金也就越多.但同时也要兼顾那些灰色关联系数较小的班级,于是为了体现公平性,笔者又引入了另外的一个函数f2(N).
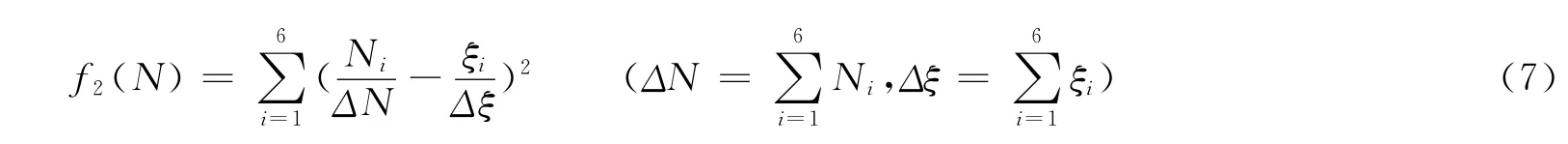

(8)式中,认为在决策偏好系数β∈[0,1]不变的情况下,f(N)越大则认为该种分配策略越好.
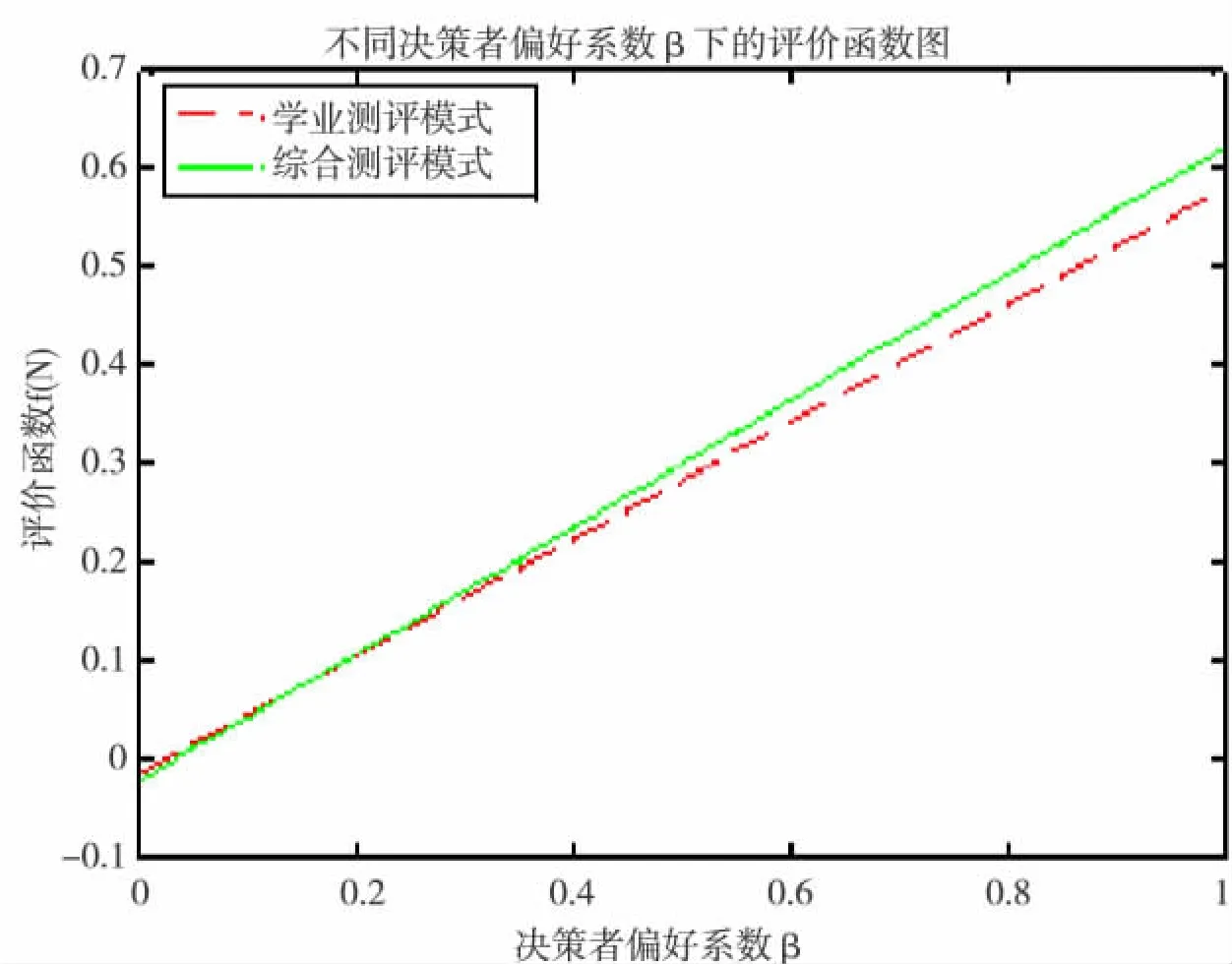
图1 评价函数f(N)在不同决策偏好系数β下的变化情况曲线图
根据从图1中反映的计算结果,可以得到如下关系:
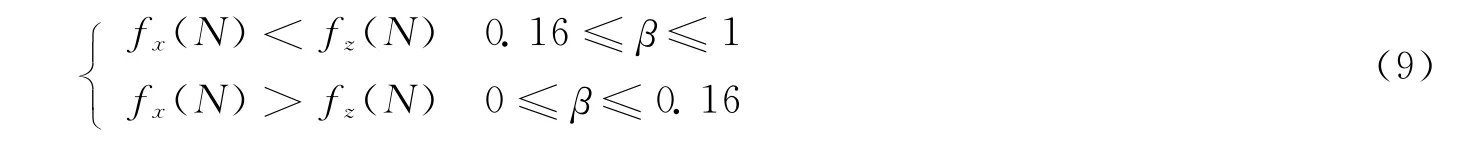
其中,fx(N)表示学业测评模式下的评价函数f(N),fz(N)表示综合测评模式下的评价函数f(N).于是,在决策者偏好系数β∈[0.16,1]时,采取综合测评模式下的分配奖学金方式更加公平、有效;而决策者偏好系数β∈[0,0.16)时,则应采取学业测评模式下的奖学金分配原则.
当然,基于不同决策者偏好系数β∈[0,1]下的评价函数f(N)带有一定的主观性,对应于不同的决策偏好程度.但从图1中可知,在多数情况下综合测评模式是优于学业测评模式的,这与实际生活是相一致的,多数学校也正是采取该模式下的奖学金分配制度,在一定程度上也证明了该评价方法的合理性.
4 问题分析的改进
在该模型的建立过程中,并未考虑各获奖学生之间的成绩比较情况,按正常情况来说:如果每个班获奖同学之间的成绩差距较小,则反映出该分配方案是最有效和最公平的.这里并没有考虑这方面的影响因素,于是利用偏差平方和来反映获奖学生之间的差别情况,假设Re sultij表示第i班第j个获奖学生的测评成绩,则总得偏差平方和为
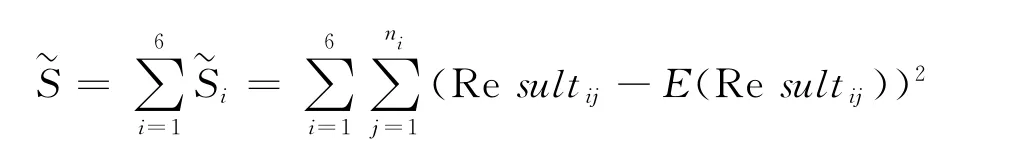
其中ni表示第i班获奖学生总数,E(Re sultij,表示第i班获奖学生测评成绩的期望.于是在评价函数f(N)中可以引入偏差平方和˜S,并通过一些有效的方法来确定f1(N)、f2(N)与˜S三者之间的权重大小,以此作为新的评价函数^f(N),提高模型的应用范围和精度.
[1] 彭志奇,戴彬.基于熵权的灰色关联分析方法在供应商选择中的应用研究 [J].商业研究,2008,526:49-50
[2] 高尚.席位分配的最大熵法 [J].数学的实践与认识,1996,26(02):73-75
[3] 林健良.席位公平分配的最小极差法的改进 [J].华南理工大学学报:自然科学版,2002,30(03):21-23
[4] 万中,罗汉.席位分配问题的数学模型 [J].湖南大学学报:自然科学版,2001,28(06):5-9
[5] 贺明峰,陈俐羽,于柄林.席位分配问题的一种新算法 [J].数学的实践与认识,2007,37(04):83-87
[6] 汤丽华,赵吴静.基于熵的水质综合评价的相似插值模型 [J].中国管理科学,2006,14(10):91-94
[7] 骆文辉,杨建军.基于灰熵方法的综合评估 [J].指挥控制与仿真,2008,30(02):74-77
[8] 邓聚龙.灰色系统基本方法 [M].武汉:华中理工大学出版社,1987:40-78
[9] 曾繁伟.煤炭企业管理水平的灰色关联度综合评价法 [J].河北煤炭,2000,(02):55-56
