变上限积分的等价无穷小研究

蒋 政，钱学明

（1．无锡科技职业学院基础部，江苏 无锡214028；2．无锡科技职业学院物联网技术学院，江苏 无锡214028）

等价无穷小替换是极限运算中简化函数的一种重要方法．适当的等价无穷小替换可以使极限计算化繁为简，事半功倍．因此，该方法广泛应用于各类极限计算问题，受到广大师生的青睐．但是，在等价无穷小替换中，有一类函数的等价无穷小鲜有讨论，即变上限积分的等价无穷小．文献［1］中首先提出了变上限积分的等价无穷小，但仅仅给出了一些特殊情形下的等价无穷小替换公式，并未从理论上详加论证．文献［2］给出了较文献［1］一般的公式，并给予了简单的证明，但其中定理的论述有误，且公式仍有其局限．

本文拟通过引入带有Peano型余项的Taylor公式，来获得一类变上限积分等价无穷小的一般公式，并给予证明．其结果具有一般性，现有文献 ［1－2］的结果，都可看作本文结果的特殊情形．最后，将举例说明本文提出公式的有效性．

1 预备知识

α，β都是在同一自变量同一变化过程中的无穷小 （量），且α≠0．而lim表示的则是该变化过程的极限．

引理1［3］在自变量的同一变化过程中，α～β的充分必要条件是β＝α＋ο（α）．

引理2［3］等价无穷小的等价替换定理：在自变量的同一变化过程中，α，α′，β，β′都是无穷小，且α～α′，β～β′，如果

2 主要方法及证明

以下，就来讨论变上限积分的等价无穷小，并给出相关的一般性定理．

定理1 若函数f（t）在t＝t0处n阶可导，则

的图像，直观、明了．因此，定理1的

结论在变上限积分的教学中具有重要的作用．

而在含有变上限积分的极限问题中，通常会有其它一些约束条件．这些条件的引入，可以获得以下结论．

进一步，特殊地取φ（x）＝x，则可得到以下定理4．

定理4 若函数f（t）在t＝0处n阶可导，且f（0）＝f′（0）＝f″（0）＝ … ＝f（n－1）（0）＝0，f（n）（0）≠0，则当x→0时有

于是，可得以下结论［3］．当x→0时，

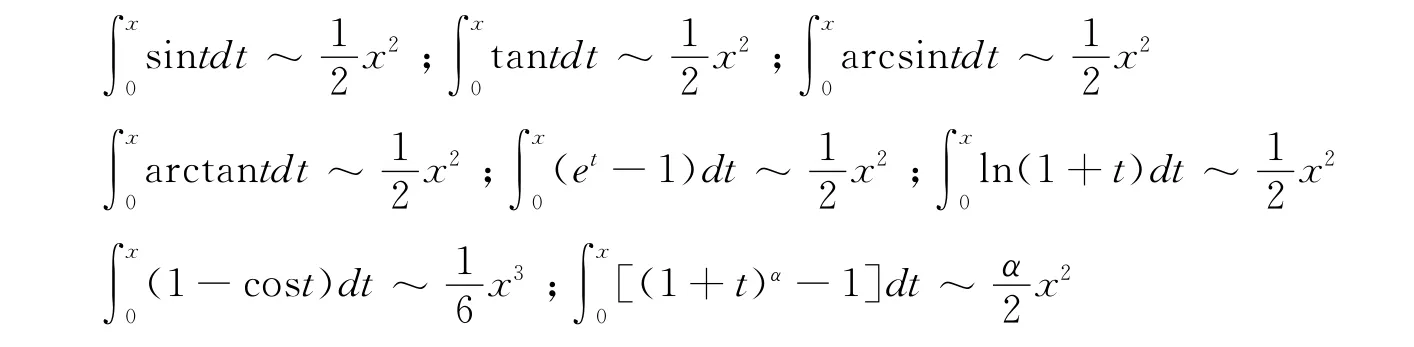
显然，文献 ［1］中的诸多结论，均可由本文定理4获得．

3 应用举例

上述定理在含变上限积分的极限问题中，结合等价无穷小替换，可以极大地简化运算．

［1］ 于延荣．关于等价无穷小代换的若干结论 ［J］．工科教学，2001，（04）：100－102

［2］ 杨爽．一类变上限积分的等价无穷小量研究 ［J］．科技信息，2010，23（04）：117

［3］ 杨春玲，张传芳．变上限积分的等价无穷小 ［J］．高等数学研究，2004，（06）：43－44