基于势流理论的集装箱船型球首优化设计研究＊

张宝吉 马 坤 纪卓尚

（上海海事大学海洋环境与工程学院1） 上海 201306） （大连理工大学船舶工程系2） 大连 116024）

基于势流兴波理论的Rankine源法是当前预报船舶兴波问题的主要手段，目前，国外的一些专家、学者已能够成功的运用该方法进行兴波阻力预报和船型优化，铃木和夫［1－2］采用该方法分别计算了Wigley数学船型、系列60船型和双体船的阻力性能，并将计算结果同模型试验相比较，验证了该方法的有效性；同时，铃木和夫又将该方法结合二次规划法对Wigley数学船型和系列60船型进行全船优化［3］，获得了令人满意的结果.我国的一些研究机构也取得了一定的成果，陈京普［4］等将改进的Dawson法用于集装箱船的船型优化上，达到了预期的效果；程明道［5］应用线性兴波数值方法在尾板的优化方面进行了有益的尝试；张红玲［6］等采用CFD计算软件Shipflow对VLCC进行线型优化也取得较好效果.张宝吉［7］采用非线性规划法研究Wigley船型的最小阻力问题.本文对某集装箱船型的首部分别做三种改型，得到三个初始船型，然后，以势流兴波阻力Rankine源法为基础，选择非线性规划法为优化方法，分别对这三个初始船型进行优化计算，获得三个带球首的改良船型，通过分析、比较这三个改良船型的阻力性能和球首形状，表明不同大小的球首和形状对阻力性能的影响各不相同，从而为理论确定球首的大小和位置提供有益的借鉴.

1 船型优化数学模型的建立

1.1 目标函数

选取总阻力Rt为目标函数，Rt用兴波阻力Rw和相当平板摩擦阻力Rf之和来表达，即

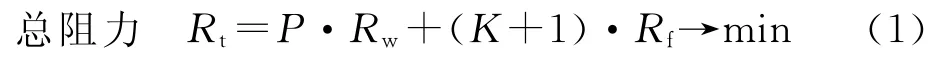
形状影响系数K按下式计算

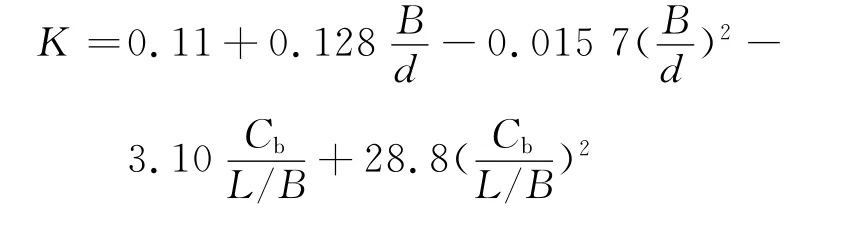
Rw采用Rankine源法来计算

式中：Cw，l为基于L2的兴波阻力系数；L为船长；B为船宽；d为设计吃水；Cb为方形系数，U∞为航速；ρ为流体的质量密度；修正系数P取对应于初始船型设计航速点的兴波阻力试验值与理论计算值之比.

Cf0为平板摩擦阻力系数

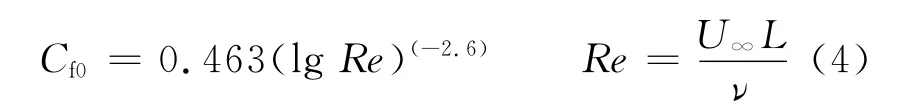
式中：Re为雷诺数；ν为流体的运动粘性系数；S为湿表面积，根据船体表面坐标进行积分求得.

1.2 设计变量

本文优化设计范围取船体首部，其中第一和第二种方案的优化设计范围从第18站到船首最前端，如图1所示；第三种方案的优化设计范围从第15站到第20站，去掉原来的球首，如图2所示.且设计水线处、船底、设计范围的前后端部为固定.

图1 第一、第二方案设计变量范围

图2 第三方案设计变量范围

改良船型的形状y（x，z）采用在初始船型f0（x，z）的基础上乘上一个修改函数w（x）来表达［3］

船型修改函数w（x）是N阶多项式函数，任意剖面上的肋骨线可以通过样条插值获得，在优化过程中，ai作为设计变量.w（x）必须满足下列条件

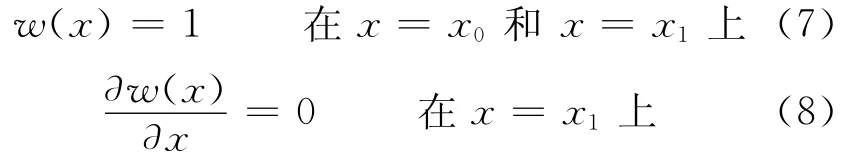
系数ai满足下列关系

1.3 约束条件

本文选取如下2个基本约束条件：（1）所有型值均为非负值，即：1.001B／2≥y（i，j）≥0.式中：y（i，j）为船体表面坐标值：（2）排水体积约束：1.005▽0≥▽≥0.995▽0，其中，▽，▽0分别为改良船型和初始船型的排水体积.

1.4 优化方法

本文选用非线性规划法中的SUMT内点法进行船型优化，首先把数学模型转化为无约束问题，然后选择直接搜索法中的梯度下降法寻找极小值点，获得最小阻力船型.

2 算 例

本文以某集装箱船为例，分别对其首部进行了三种改型，得到初始船型A、初始船型B和初始船型C，然后分别进行优化设计得到改良船型A、改良船型B和改良船型C.船体网格分别划分成23×11＝253，23×11＝253，20×11＝220；根据Dawson的网格划分经验，自由面网格的区域半宽取为约3L／8，上游伸展L／4，下游向后延伸0.25个波长，整个水面网格顺流倾斜45°，船首和船尾附近网格均加密，自由面网格布置如图3所示，自由面网格分别划分成44×16＝704，48×16＝768，44×16＝704；初始船型主要参数如表1所列.

图3 集装箱船自由面网格布置

表1 集装箱船主要参数

三种方案得到的优化计算结果如表2所列，从表中可以看出，在设计Fr＝0.26时，三个改良船型阻力都有不同程度的降低，表明该计算方法能够正确地识别船型变化对兴波阻力的影响，从而证实该方法用于船型优化的可行性.其中改良船型A的阻力降低的最小，改良船型B和改良船型C降低的较多.改良船型的湿表面积、摩擦阻力和排水体积没有发生太大变化，从改良船型的横剖线和水线图上也能反映这一点.

表2 三种方案的优化计算结果

初始船型和改良船型的兴波阻力系数曲线比较如图4～图6所示，从图中可以看出，改良船型和初始船型的兴波阻力系数曲线波动趋势基本一致，在设计Fr＝0.26的一定范围内，改良船型的兴波阻力比初始船型有了明显的降低.

图4 改良船型A和初始船型A的兴波阻力系数曲线

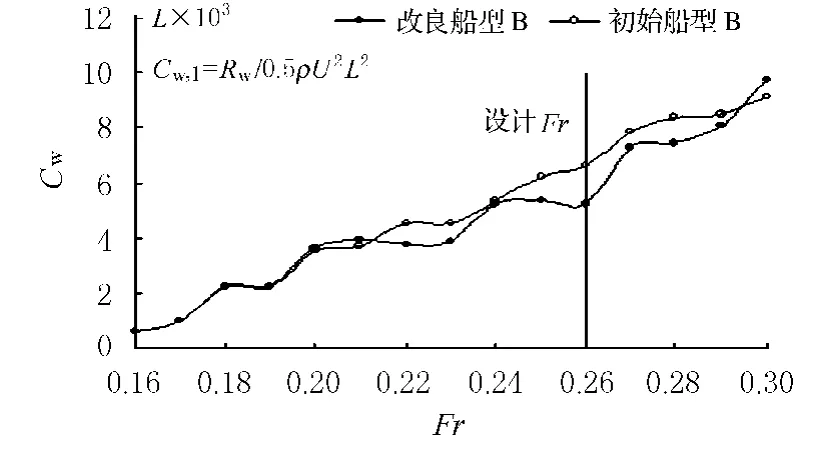
图5 改良船型B和初始船型B的兴波阻力系数曲线

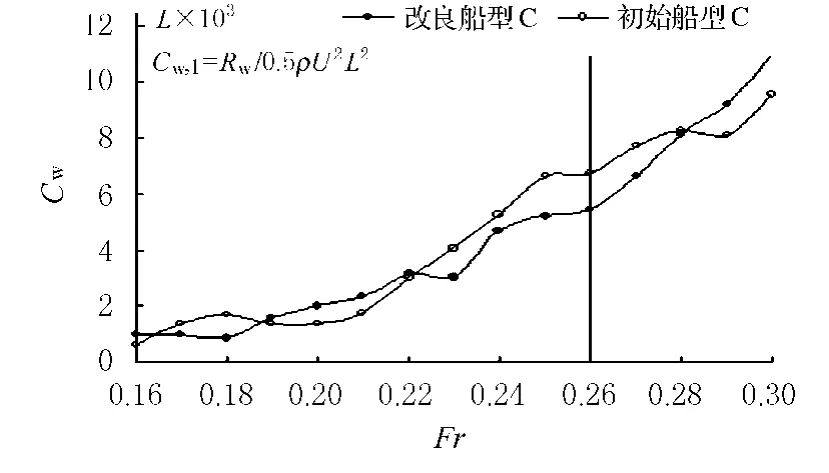
图6 改良船型C和初始船型C的兴波阻力系数曲线

初始船型和改良船型的波浪剖面图如图7～图9所示，从图中可以看出，三种改良船型的首波高并没有降低，有的甚至升高了，尾波却有了不同程度的降低，究其原因，主要有以下几点：（1）波浪剖面是采用在船体附件的自由面波高，并不是在实际的船体上，特别是在尾部；（2）船体的首、尾部区域线型复杂，受到强烈的非线性影响，线性化的自由表面条件不能完全模拟实际的边界条件；（3）船首、船尾区域的网格划分的不够精确，不能有效模拟该区域流场的实际情况.

图7 改良船型A和初始船型A的波浪剖面图

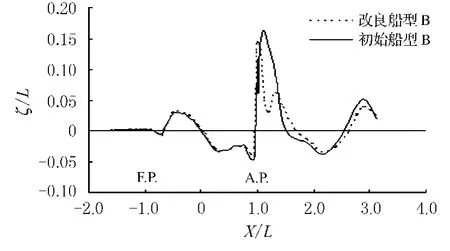
图8 改良船型B和初始船型B的波浪剖面图

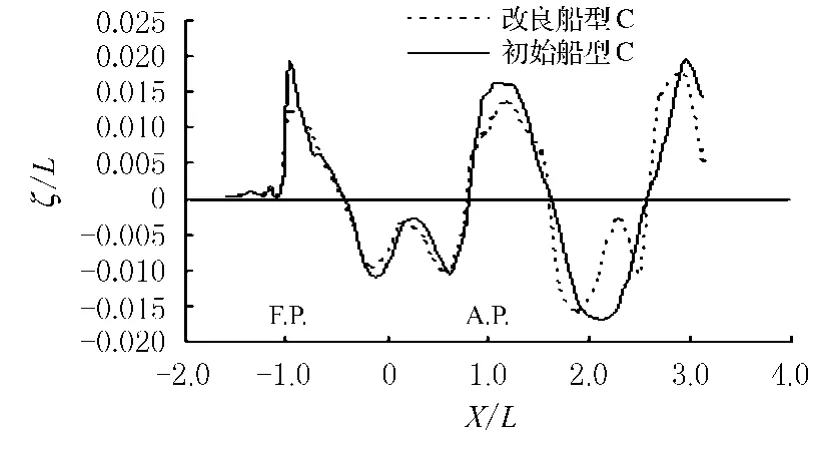
图9 改良船型C和初始船型C的波浪剖面图

初始船型和改良船型的自由面波形图如图10～图12所示，从图中可以看到有明显的开尔文波系形状，出现了横波和散波，但改良船型的波形图也比初始船型更加清晰.

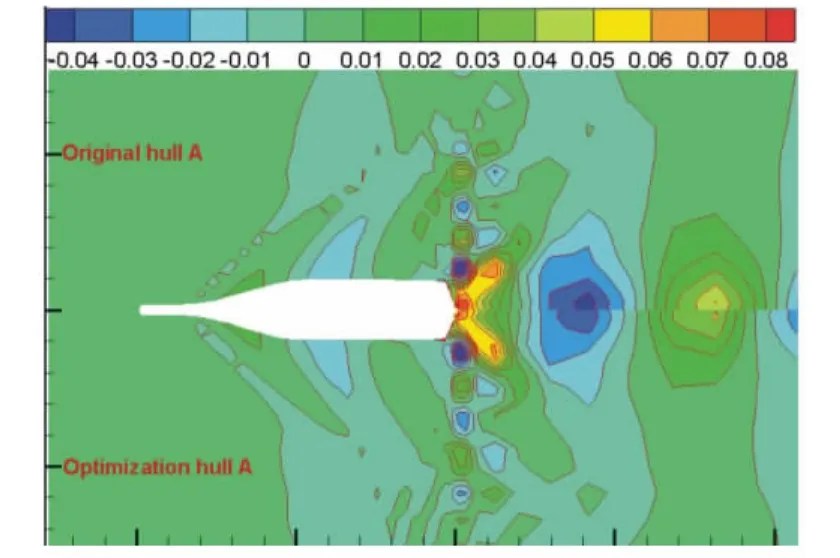
图10 初始船型A和改良船型A的自由面波形图

图11 初始船型B和改良船型B的自由面波形图

图12 初始船型C和改良船型C的自由面波形图

3 结束语

根据本文的设计方案，采用Rankine源法对其进行优化设计，虽然得到了性能优良的带球首船型，但该方法也存在一定的局限性，由于自由面条件的线性化假设，使计算结果和试验值有一定的偏差，如果能够把船体和自由面条件的非线性影响全部考虑进去，将会得到更符合实际的结果，这将有待于以后的进一步的探讨.

［1］Md.Shahjada Tarafdera，Suzuki K.Numerical calculation of free－surface potential flow around a ship using the modified Rankine source panel method［J］.Ocean Engineering，2008，35（5－6）：536－544.

［2］Kai K S H，Kashiwabara S.Studies on the optimization of stern hull form based on a potential flow solver［J］.Journal of Marine Science and Technology，2005，10：61－69.

［3］Saha G K，Suzuki K，Kai H.Hydrodynamic optimization of ship hullforms in shallow water［J］.Journal of Marine Science and Technology，2004，9：51－62.

［4］陈京普，朱德祥，刘晓东.兴波阻力数值预报方法研究及其在集装箱船船型优化中的应［J］.水动力学研究与进展.2006，21（1）：113－121.

［5］程明道，刘晓东，何术龙，贺五洲.方尾舰船兴波阻力计算及其应用［J］.船舶力学，1999，3（1）：6－12.

［6］张红玲，朱丽萍，钟应华.应用计算流体力学进行VLCC船型的线型优化［J］.上海造船，2006，67（3）：5－8.

［7］张宝吉，马 坤，纪卓尚.基于非线性规划法的最小阻力船型优化设计［J］.武汉理工大学学报：交通科学与工程版，2010，34（2）：358－361.