车辆数目未知的带时间窗口的车辆路径混合遗传算法＊

曹二保 汤春华

(湖南大学经济与贸易学院1) 长沙 410079) (湖南涉外经济与贸易学院商学部2) 长沙 410205)

车辆路径问题(vehicle routing problem, VRP)由Dantzing[1]于1959年提出,属于经典的复杂组合优化问题.而VRPTW问题是在VRP问题的基础上加上时间窗口约束,它是强NP难题[2],对它的求解主要集中在启发式算法上.本文提出了一种求解VRPT W问题的混合优化算法,遗传算法(genetic algorithm)[3]和邻域搜索算法(neighborhood search)[4]是求解VRP问题的常用方法.邻域搜索算法求解速度快,但容易陷入局部最优解,因而解的质量不高;而遗传算法具有较好的全局搜索能力,可以用极快的速度达到最优解的90%左右,要真正达到最优解则需要花费很长时间,同时遗传算法的设计有时比较复杂;基于邻域搜索的混合遗传算法是综合了遗传算法和邻域搜索算法各自优势的全局搜索算法,它既具有遗传算法的全局搜索能力,又有高效的局部搜索能力,使两种算法的优势得到互补.

1 问题描述及数学模型

带时间窗口的车辆路径问题(VRPTW)的一般表述为：配送中心拥有相同容量的K辆车,车的最大负荷为q,现有n个顾客的运输任务需要完成,设V={1,2,…,k},C={1,2,…,n},N= {0,1,2,…,n+1},0和n+1表示配送中心,第i个顾客的需求量为di(i=1,2,…,n)且有max di≤q,完成顾客i的任务需要的时间为T,且任务i必须在时间窗口[ai,bi]内完成.ai为任务i的最早开始时间,bi为允许最迟开始时间.若车辆到达顾客i的时间早于ai,则车辆需在i处等待,如果到达时间晚于bi,则任务将被延迟,每个顾客能且只能由一辆车一次完成运送任务,每辆车从配送中心出发完成运送任务后最终都回到配送中心,最终目标有两个：(1)所使用的汽车数目最少;(2)所使用的汽车总的运输距离最短.其中：第一目标高于第二目标,也就是说,需要更少数目车的解总比需要更多车的解要好,而不管第二目标的值如何.这主要是由于多派一辆汽车的成本较大的缘故.tij为汽车从客户i到客户j的行驶时间(正比于i和j之间的欧几里得距离dij);sik为汽车k开始为客户i服务的时间,令s0k=0,如果汽车k没有为客户i服务,则sik没有任何意义.变量 xijk=

则VRPTW的数学模型可以表示为

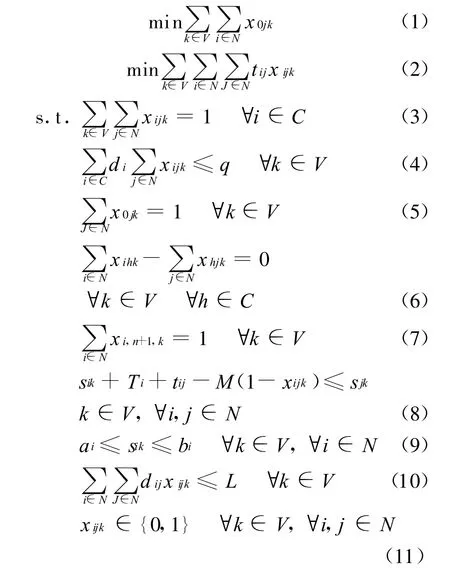
在上述表达式中：式(1)为使需要的汽车数目最少;式(2)为使所有的汽车走过的路程(时间)最短;式(3)为每个客户仅能被访问一次;式(4)为被调用的汽车都满足负载要求;式(5)～(7)保证每辆汽车从出发点出发,访问客户后,最终回到出发点;式(8)为汽车k在从客户i向客户j行驶的过程中,在时间sik+Ti+tij之前不能到达客户j,其中M是一个较大的标量;式(9)为汽车为客户i服务的开始时间必须在其时间窗口内;式(10)为最大距离约束,dij为顾客i到顾客j的距离,L为每辆车行驶的距离上限;式(11)为整数化的约束.该模型通用性很强,经过参数的不同设定,可以将其转换为其他组合优化问题的数学模型.例如,设定ai=0,bi=M(是一个很大的数),则可以把约束式(8)和(9)去掉,这样VRPTW模型就变成了普通的VRP模型;如果只提供一辆汽车,则该问题就是TSP;如果有多辆汽车可利用,且附加条件t0,j=1,∀j∈C和tij=0,就得到了装箱问题的数学模型.

2 编码

采用比较直观的自然数编码,用矢量(l1,l2,…,ln)表示染色体G.其中,元素(基因)l1为[l,n]之间的一个互不重复的自然数,随机产生一组染色体Gh(h=1,2,…,k).其中：k为每一代种群中的个体数目,即为种群规模,Gh各不相同,它为第一代种群.首先根据经验对完成配送任务可能需要的车辆数目进行设定,设为m,对于某个个体,设其对应的配送路径方案的配送路径条数与m之差为J,若配送路径条数不超过m,则取J=0,表示该个体对应一个可行解;然后将m的取值逐一减小,直到减小m后不能得到满足所有约束的可行解;此时m即为最小的车辆数目;若配送路径条数大于m,则J＞0,表示该个体对应一个不可行解).若设定的m只有不可行解,将m的取值逐一增大,直到增大m后能得到满足所有约束的可行解.设个体的目标函数值为Zh,将J看成该个体对应的配送路径方案的不可行路径条数,并设对每条不可行路径的惩罚权重为pw(该权重可根据目标函数的取值范围取一个相对较大的正数),根据式(2)可以得到该个体的目标函数值Zh,若染色体对应不可行解,则其适应值函数为越大,表明Gh的性能越好,对应的解越接近最优解.

3 VRPTW的混合遗传算法

3.1 遗传操作

采用比例选择和精华模型相结合的选择策略.将每代种群k个染色体按 fh值排序 ,将 fh值最大的染色体复制一个直接进入下一代.下一代种群中剩下的k-1个染色体用轮盘选择法产生.这样,可以保证最优个体可以生存到下一代 ,既给了适应度较大的个体较大的机会进入下一代,又避免了个体间因适应值不同而被选入下一代的机会悬殊.本文设计了一种新的前置交叉算子.用9个顶点为例说明交叉原理：设P1={1 2 3 |4 5 6 7|8 9};P2={4 5 2|1 8 7 6 |9 3}.其中：|表示交叉点,子个体按以下方式确定——取P2中的2个交叉点中间的点放在子代C1的开始处,其状态暂时为C1={1 8 7 6 X X X X X}.对未确定的位置X,在P1中找到暂时没有在C1中出现的离6最近的点3,将3放在6的后面,从左到右将P1中未出现的点移到C1中,最后C1为{1 8 7 6 3 4 5 9

2}.前置交叉操作过程如图1所示.

图1 交叉操作

给定2个相同的染色体,经过新的交叉算子仍然可以产生不同于父体的新个体 ,这就是说 ,由于新颖交叉算子的引入 ,当个体都相同时 ,仍然能够进行迭代进化 ,继续寻找问题的优化解 ,跳出了局部最优解 ,克服了“早熟收敛”的缺点.而以往的交叉算子 ,当个体都相同时无法继续迭代进化 ,只能寻找到问题的局部最优解.如则经过新的交叉算子后两个子代为{1 8 7 6 3 4 5 2 9}.

3.2 邻域搜索算法

本文主要考虑的邻域结构有 NS={Nswap,},经过交叉操作后用作为变异操作, Nswap是随机互换染色体中的2个基因,Ninversion随机逆转染色体中的基因.具体操作过程如图2、图3所示.

图2 互换操作

图3 逆转操作

4 基于邻域搜索的混合遗传算法

按照前文所述的方法产生初始种群S,种群规模视客户数量来确定,在进行遗传操作过程中,结合了约束检验机制,即无论是交叉还是变异操作,每当新的个体产生的时候都要检验是否满足相关约束,如最大行使时间、容量、时窗等,若满足则保留,否则弃之.选择操作执行的是比例选择和精华模型相结合的选择策略,具体算法步骤如下.

步骤1 i=0,pi为空集.pi用来保存每代中的最好解.

步骤2 产生某代初始群体si.

步骤3 计算适应度,若满足最优准则,则转步骤8.

步骤4 执行选择操作,i=i+1.

步骤5 以一定的概率进行交叉操作和变异操作.

步骤6 产生当前最好解.

步骤7 对当前最好解进行邻域搜索中的逆转操作,将改善的当前解保存于pi中,转步骤3.

步骤8 pi中的最优个体即为问题的解或近似解.

5 算例分析

有8个分店和1个配送中心,各分店的需求量为di(单位：t).服务时间Ti(单位：h)以及分店要求的服务时间范围[ai,bi],由表 2给出.这些分店由容量为8 t的车辆完成配送 ,汽车的行驶速度设为50 km/h,配送中心与各分店间的距离(单位：km),由表1给出.要求合理安排车辆的行驶路线,使总的车辆数目和总的行使距离最短[5-7].

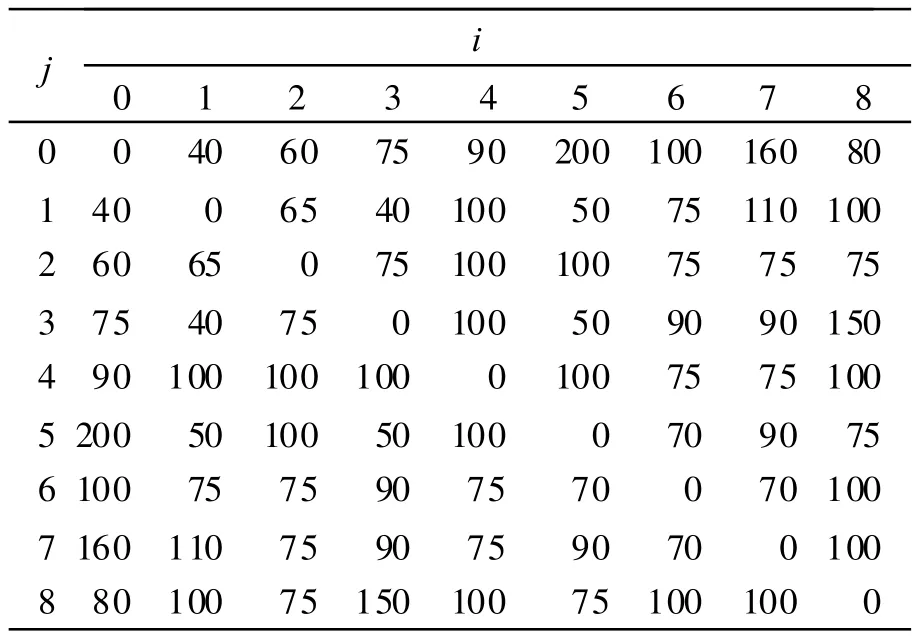
表1 分店间及分店与配送中心的距离

表2 任务的特征及需求

表3 运行500次的平均计算结果

运用Matlab语言对上述混合遗传算法进行编码,设置遗传算法的种群规模为40,交叉概率为0.9,变异概率为0.1,使用Pentium 4,3.06 GHz微机运行程序,分10次实验得到迭代500次的算法的平均结果如表3(其中标准差为计算10次的结果),得到的最好结果如图4所示.

运行500次后得到的40条染色体表现为相同的配送方案,达到最优解的概率为100%,最终结果为：总的路径长度为910 km,使用3辆车完成配送任务,其中第一辆车的配送线路为：0-8-5-7-0,离开配送中心时的实际装载量为7 t,满载率为87.5%,路径长度为405 km..第二辆车的配送线路为：0-6-4-0,离开配送中心时的实际装载量为7 t,满载率为87.5%,路径长度为265 km.第三辆车的配送线路为：0-3-1-2-0,离开配送中心时的实际装载量为8 t,实现满载,路径长度为240 km.本文的算法与其他优化算法找到的最好结果比较如表5.

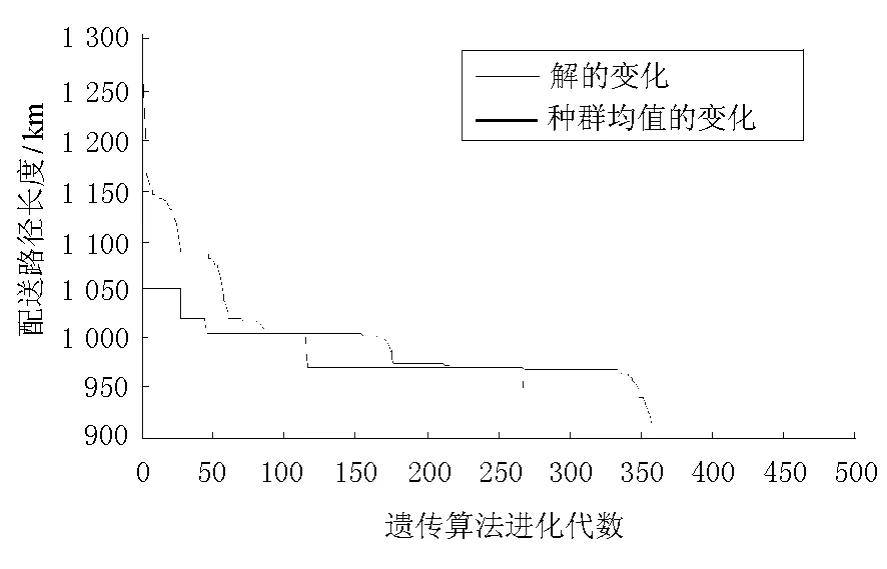
图4 经过500次迭代后的运行结果

表5 本文算法与其他优化算法的最好结果比较

此外,用本文的算法来优化[8]中的算例,在种群规模为40,进化300代后,无时间窗时需要的车辆数目为2,最优路径长度为655 km,最优行驶方案为：0-1-3-5-8-0;0-2-6-7-4-0;运行时间为1.625 0 s,且达到最优解的概率为100%.带时间窗口时,在种群规模为40,进化500代后,需要的车辆数目为3,最优路径长度为910 km,最优行驶方案为：0-8-5-7-0;0-6-4 -0;0-3-1-2-0;且运行时间为5.781 0 s.

由上述比较分析可知,本文的基于邻域搜索的混合遗传算法在求解质量、求解速度、解的稳定性等方面明显优于其他算法.

6 结束语

运用本文提出的基于邻域搜索的混合遗传算法求解带时间窗口的车辆路径问题,能使完成配送任务所需的车辆数目和总路径长度得到同时优化,该算法既具有遗传算法的全局搜索能力,又具有邻域搜索算法的局部搜索能力,实验结果表明该算法具有很强的寻优能力,具有较强的克服陷入局部最优的能力,算法的求解质量高,具有较快的收敛速度,减少问题的约束后,该算法同样能有效求解它们.

[1]Dantzing G,Ramser J.The truck dispatching problem[J].Management Science,1959,10(6)：80-91.

[2] Savelsbergh M.Local search for routing problem with time windows[J].Annals of Operations Research,1985,16(4)：285-305.

[3] Potvin J Y,Bengio S.The vehicle routing problem with time windows——part II：genetic search[J]. INFORMS Journal on Computing,1996,8(2)：165-172.

[4] Liu Fuhhwa,Shen Shengyuan.A route-neighborhood-based metaheuristic for vehicle routing problem with time windows[J].European Journal of Operational Research,1999,118(3)：485-504.

[5]李 军.车辆调度问题的分派启发式算法[J].系统工程理论与实践,1999,117(1)：27-33.

[6]李 宁,邹 彤,孙德宝.带时间窗车辆路径问题的粒子群算法[J].系统工程理论与实践,2004,24(4)： 130-135.

[7]李 军.有时间窗车辆路线安排问题的启发式算法[J].系统工程,1996,14(5)：45-50.

[8]邹 彤,李 宁,孙德宝.不确定车辆数的有时间窗车辆路径问题的遗传算法[J].系统工程理论与实践, 2004,24(6)：134-138.