大气波导中折射指数的预测预报技术研究

赵小龙，黄际英，王玉平，鲍丽红

（1.天水师范学院，甘肃 天水 741001；2.西安电子科技大学，西安 710071）

大气波导是由于近海面大气修正折射率随高度的反常下降，使电波射线向下弯曲的曲率大于地球表面的曲率，从而将电磁能量陷获在波导结构内的电磁波异常传播现象。大气波导的出现不仅可以使电磁波偏离原来的传播方向，而且能够使电磁波以较小的衰减沿波导传播到很远的地方，对无线电管理、雷达及微波通信等电子系统应用、电子战攻防手段等影响显著。因此，实时、准确地预测预报大气波导折射指数成为电子系统性能评估和系统设计的前提，以及获取战场电磁优势、掌握战场电磁频谱使用和控制权的关键[1－2]。

1 中国海区大气波导环境

我国位于亚洲大陆的东南部，雄踞北太平洋西侧，邻近有渤海、黄海、东海和南海四大海区，海岸线总长度达18 000 km，海洋国土面积近3 000 000 km2，海域辽阔。美国研究者[3]根据世界各个地区多年的气象观测数据利用出现概率等高线绘制了陷获L，S和X 波段的表面波导区域分布示意图（如图1 所示）。从图1 中可以看出我国沿海海域是蒸发波导的高概率发生区。我国自1990年以来，经过对全国各探空站探空数据的统计分析将我国波导气候区分为4 个波导频繁区和4 个无波导区[4]。通过对我国波导频繁区和无波导区的划分，可以看出我国的西北内陆区和沿海及邻海区是波导高概率区。

图1 表面波导的覆盖区域Fig.1 Distribution of surface duct on world map

刘成国[5]利用 1990—1992 年北纬 0°～30°、东经100°～130°海域的海洋船测数据研究了蒸发波导环境特性，测量数据分析表明该海域是蒸发波导高概率发生区。1997 年10 月，中国电波传播研究所在东经115°～120°、北纬23°～25°之间的东南沿海展开了1个月的对流层大气波导探测试验。通过利用59 型探空仪探测对流层大气剖面、ADAS 系统测量近地层大气结构、气象仪测量气海界面要素对多个地点进行测量。试验分析表明，这些地区蒸发波导结构的出现概率超过80%，平均高度在10 m左右；高纬度海域蒸发波导出现对应的气海界面通常处于不稳定状态，而低纬度海域的地区通常靠近中性状态。通过大量的试验测量研究，我国的科研工作者研制成功了覆盖我国陆上各地和东海、南海的对流层波导环境数据库，取得了初步满足我国各种无线电应用系统急需的对流层波导环境特性的信息。深入研究蒸发波导环境预测理论、提高蒸发波导预测预报技术的精确度已成为下一步的工作重点。

2 折射指数预测预报技术

为有效预测、评估大气波导环境中的雷达探测距离和微波通信的最大距离，20世纪70年代美国经历了一场开发折射效应评估系统的热潮，开展了多种对海洋大气折射率分布的预测和预报研究。其中，最直接的方法就是利用微波折射率仪、无线电探空仪、风筝式系留气球、直升机等对海洋边界层大气各项气象参数进行测量，但由于空间、时间的低采样率很难获得近海平面10～100 m 间表面层高度上温度、湿度的变化，难以满足实际应用对蒸发波导高度预测的需要。出于测量方法的易用性和实时性等方面的考虑，利用海面气象要素预测蒸发波导高度的方法有了很大发展，形成了多种比较实用的预测模型。然而，几乎所有的模型都是基于大气边界层的Monin-Obukhov相似理论，截止目前它仍是根据近海平面几百米内任意高度处温度、湿度信息确定蒸发波导高度和折射率空间分布的经典理论，而在试验研究和理论研究中提出的Paulus-Jeske（P-J）模型、MGB 模型、Babin 模型、LKB 模型、RSHMU 模型、ECMWF 模型、COARE 模型等也在不断提高蒸发波导高度的预测精度[6－7]，满足了近海面电波传播预测的要求。但是这些模型在相似理论应用上显著不同，通过相同条件下的对比试验表明：Babin 模型使用了精确的整体相似表达式，并采用了小风速相似理论拓展技术和湿度的盐度订正技术，结果优于P-J模型和MGB 模型。对海上大气表面层建模更通用的方法是 Liu，Katsaros 和 Businger 在 1979 年提出的LKB 模型。LKB 模型通过海面上确定高度处的风速、空气温度、相对湿度以及海面温度和大气压强利用相似关系确定了动量、热和湿度通量，这些量与表面层的高度几乎无关，进而得到风速、温度和比湿的垂直剖面。 COARE（Coupled-Ocean Atmosphere Response Experiment）算法是基于Monin-Obukhhov相似理论对Liu 等算法上的又一突破。RSHMU 模型、ECMWF模型也分别被用于乌克兰和欧洲的气象预报中心。1978 年利用Jeske 模型开发的综合折射效应预测系统（IREPS）装备美国海军航母用于雷达、通信、飞行操作等任务部署。美国国家气象数据中心（NCDC）也利用15 a 的海上气象观测数据及Paulus-Jeske 模型计算了292 个马士顿方区海域（10°×10°）蒸发波导高度的频数分布，开发出了工程师折射效应预测系统（EREPS）[8]。近年来，美国又将Paulus-Jeske模型用于IREPS的改进版，开发出了高级折射效应预测系统（AREPS）。1999年澳大利亚提出了大气边界层折射率剖面的同化模型，并开发出了对流层折射效应预测系统（TREPS），用来设计预测海上舰船、潜艇和海上巡逻飞机上的侦察雷达、电子支援系统性能[9]。然而，利用同一理论不同研究者在不同试验中的版本都有些差异，其中应用于IREPS 的Jeske 模型对波导高度估计的均方根误差大于7 m，应用于AREPS的Paulus-Jeske修正模型预测误差降低到4.5 m，Ivanov 利用1983－1984 年的大西洋和印度洋的实测数据，采用LKB 模型、COARE 模型、RSHMU 模型、ECMWF 模型可将稳定层结5～20 m 范围内的蒸发波导高度估计误差降低至3.5 m，不稳定层结的误差降至2.5 m。因此，对于最优算法的选择一直也没有定论，主要依赖于更高精度的气象参数的测量[7]。

1992—1993 年美国国家海洋和大气管理署（NOAA）开展的耦合海洋大气响应试验（COARE）[10]，通过直接获取通量参数的微气象学传感器，获取风速、温度、湿度遥感器，声测风速计、温度计、快速响应的红外湿度计，以及多普勒雷达、声纳、激光云高计、微波辐射计、日射强度计、地面辐射强度计、无线电探空测风仪等多种测量手段，研究了表面通量、边界层动态特性、云和辐射的相互作用及输送过程，该试验被证明对卫星校准及有效性的预测非常有用。1992年美国又开展了一系列观测仿真试验以评估近地大气折射对低轨卫星上GPS 信号的影响，并利用地卫空间GPS 信号传播路径的弯曲遥感近地水汽、温度变化以获取大气折射率垂直剖面。1993－1994年，美国海军指挥控制和海洋监视中心（NCCOSC）联合海军航空兵作战中心（NAWC）、海军研究实验室（NRL）、海军研究生院（NPS）、美国国家海洋和大气管理署（NOAA）、宾夕法尼亚州立大学应用研究实验室（PSU/ARL）、约翰霍普金斯大学应用物理实验室（JHU/APL）等多家单位开展了沿海大气折射率变异试验（VOCAR）[11]，利用3 个边界层剖面测量站、3 架直升机、8个无线电探空仪以及大量的地面气象观测站测量研究了折射率水平不均匀、折射条件与大气属性关系以及新的无线电遥感遥测技术。利用物理光学方法（RPO）的传播预测与观测数据、预测折射率结构的对比研究，对理论研究中所面对的传播预测、气象数据时空分辨率、不同传感器的测量性能等问题有了深刻认识。2001年夏季在瓦胡岛东北海岸开展的粗糙海面蒸发波导中的微波和红外传播试验，确定了相似理论对各向同性不稳定海上边界层预测的正确性。

大气折射率剖面的直接测量、基于特定高度气象参数的理论预测、GPS测量等技术由于测量精度、实时性、经费、适用海域等因素，在实际军事应用中受到很大限制。1998 年海军水面战争中心（NSWC）提出利用雷达海杂波反演来预测大气折射率剖面（RFC），并利用S 波段空间距离雷达SPANDAR 开展了Wallops 岛的测量试验。RFC 最大的优点在于使用舰载雷达作为遥感设备，利用海面雷达杂波来估计当前大气折射率剖面的垂直和水平分布，采用极大后验估计（MAP）、多仰角估计、Kalman 滤波器、多模粒子滤波器、模拟退火/遗传算法（SA/GA）、马尔科夫链蒙特卡罗采样方法（MCMC）、匹配场阵列处理方法等获取大气折射率结构[12—13]，将问题转化为参数的统计估计。利用雷达海杂波反演大气折射率剖面的预测技术与传统的基于气象参数的折射率剖面估计技术相比，不需要添加额外的气象测量设备、实时性好、军事保密性好，因而是一种极具潜力的大气折射率剖面估计新方法。

3 海杂波反演技术

利用现代工具从雷达杂波观测数据中估计表面波导折射率结构首次被Krolik 等人描述，他们将杂波反演折射率的问题通过贝叶斯判决定理转化为利用全局折射率参数和雷达测量得到的对数幅度数据的极大似然估计问题。

若将根据参数模型理论计算得到的杂波功率表示为pc（r，M），则试验观测到的杂波信号功率为[14]：

式中：Mtrue是未知的、与距离高度相关的实际环境中的修正折射率；L 是传输损耗；σ0（r）是在距离处海面的雷达散射截面；C 是考虑雷达参数后所引入的常数。若假定σ0（r），C都是不可通过推理获得的，则杂波功率的非归一化功率P′（r，m）可表示为：

式中：P′（r，m）在不同离散距离处的矢量可用P′（r，m）表示。模型参数矢量m 通过环境模型Henv（m）唯一地映射为M，所以重建参数模型的杂波功率矢量P 可用P（m）或P（M）表示，而试验测量Mobs所对应的杂波功率则表示为P（Mobs）。

根据试验观测的杂波功率Pobs与模型对应的杂波功率Pc之间的误差，利用简单的最小二乘目标函数就可对模型参数M进行优化：

为进一步分析剖面参数M 估计的不确定度，就必须确定每一个估计参数的均值、方差、边际后验概率分布等基本量。贝叶斯定理是解决杂波反演折射率等非线性反演问题中估计不确定度的有效工具，它将未知环境参数看作是具有一维概率密度和维联合概率密度的随机变量，这个概率函数可定义为试验数据矢量d 条件下的模型矢量m 的概率，即p（m|d），被称为后验概率密度函数（PPD）。具有最大概率的m 被称为最大后验概率解（MAP）。另一种方法就是最小化杂波数据d和重建杂波数据Pc（m）的最小均方误差方法，它被称为极大似然估计（ML）。由于先验信息的不充分，MAP 和ML 是一样的。利用贝叶斯公式，后验概率可表示为：

式中：p（m）表示环境参数m在试验前的先验概率，因此它与试验结果d 是相互独立的；p（d）是p（m|d）的归一化因子，也是与参数矢量m独立的。直接将式简化为：

若假定误差是一个空间非相关的零均值高斯分布函数，则似然函数可写为：

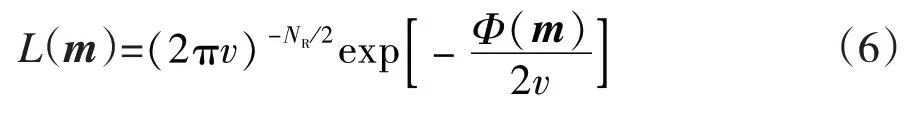
式中：v是方差。利用式（5），后验概率密度可表示为：

矢量m 是具有n 个参数的M 剖面的表示，其中每个元素mi就是第i个参数值，而每一个环境参数都可看作是未知的随机变量。因此，n维联合后验概率分布可以用所有参数的概率分布定义，而均值、方差、边际后验分布等期望值则可通过PPD得到。n个参数的折射率模型m应用于电磁抛物方程的傅立叶分步模型，在输入频率、发射高度、波束宽度、天线方向图等参数得到大气波导环境中的电磁场分布，并获得雷达杂波功率Pc（m）。与试验测量得到的杂波数据d 相比较，可得到误差函数Φ（m），借此获得似然函数L（m）。在早先的全局参数方法中，误差函数被用于穷举搜索算法、遗传算法、模拟退火算法等全局优化算法，这可使Φ（m）最小化并得到折射率模型m 的极大似然估计解[13]。若将基于Φ（m）的似然函数用于Metropolis 或Gibbs 抽样，则不仅可以得到极大似然估计解，而且能够更好地估计方差、边际概率密度、多维后验概率密度等参数的不确定度。马尔科夫链蒙特卡罗算法（MCMC）能够提供后验概率密度PPD 的无偏抽样，并保证结果在大量抽样时覆盖真实分布。但随着折射率参数模型中参数数量的增加，迫切需要高效、精确的算法以满足杂波反演折射率实时性的要求。

4 结语

世界范围的气象观测数据及我国东南沿海海域的大气波导环境测量试验表明，我国东南沿海海域是大气波导高概率发生区。大气波导环境中折射指数剖面的试验测量和预测预报技术主要有无线电探空仪、微波折射率仪、无线电掩星方法、地基GPS方法、海杂波反演技术等。基于雷达海杂波的大气折射率剖面预报技术实时性好、军事保密性好、不需要添加额外的气象测量设备，是一种极具潜力的大气波导环境预测技术，能为海上工作的雷达、通信等电子武器系统提供实时、高效、精确的性能评估。

[1]任香凝，李文计.海面蒸发波导微波超视距通信可行性分析[J].无线电通信技术，2008，34（2）：22—24.

[2]戎华，曲晓飞，高东华.大气波导对电子系统作战性能的影响[J].现代雷达，2005，27（2）：15—18.

[3]DOUGHERTY H T. Recent Progress in Duct Propagation Prediction[J]. IEEE Trans on Antenna and Propagation，1979，27（4）：542—548.

[4]刘成国，中国低空大气波导出现概率和波导特征量的统计分析[J].电波科学学报，1996，11（2）：60—66.

[5]刘成国，黄际英，江长荫.我国对流层波导环境特性研究[J].西安电子科技大学学报，2002，29（1）：119—122.

[6]ROWLAND J R，MEYER J H，NEUES M R.Time Scale R-efractive Index Measurements Within the Marine Evaporation Duct[C]//IGARSS'90. IEEE on Geoscience and Remote Sensing Symposium.1990：73.

[7]IVANOV V K,SHALYAPIN V N，LEVADNYI Y V.Determination of the Evaporation Duct Height from Standard Meteorological Data[J]. Izvestiya Atmospheric and Oceanic Physics，2007，43（1）：36—44.

[8]HITNEY V H，VIETH R.Statistical Assessment of Evaporation Duct Propagation[J]. IEEE Trans on Antenna and Propagation，1990，38（6）：794—799.

[9]PHILLIPS D M，BAKER C P.Refractivity Profile Assimilation Model for the Atmospheric Boundary Layer[R].Australia：DSTO Electronics and Surveillance Research Laboratory，1999：1—28.

[10]FAIRALL C W，WHITE A B.Integrated Shipboard Measurements of the Marine Boundary Layer[J].Journal of Atmospheric and Oceanic Technology，1997，14：338—359.

[11]ROGERS L T.Statistical Assessment of the Variability of A-tmospheric Propagation Effects in the Southern California Coastal Area[C]//International Symposium on Geoscience and Remote Sensing.IGARSS'94，1994：389—393.

[12]GERSTOFT P.Estimation of Radio Refractivity Structure Using Matched-Field Array Processing[J]. IEEE Trans on Antenna and Propagation,2000.48（3）：345—356.

[13]GERSTOFT P，Refractivity-from-clutter using Global Environmental Parameters[J]. IEEE on Geoscience and Remote Sensing Symposium，2001：2746—2748.

[14]GERSTOFT P，ROGERS L T，KROLIK J L. et al. Inversion for Refractivity Parameters from Radar Sea Clutter[J]. Radio Science，2003，38（3）：8053.