雷电产生的海洋电磁场研究中Levinson-Durbin算法实现

崔培，李琳琳，李沛剑，岳瑞永

（1.大连测控技术研究所，辽宁 大连 116013；2.海军驻航天一院军代表室，北京 100076）

海洋中存在多种电磁效应，根据场源的形式可分为自然电磁场和人为因素形成的电磁场。

自然电磁辐射是非人为因素产生的电磁波辐射。在自然电磁环境中，静电、雷电和地磁场等自然辐射是几种最主要的电磁辐射[1]。地球大气中雷电现象是海洋自然电磁场的主要场源之一。雷电产生的地磁变异，呈短暂的脉动形式，具有较强的地域性和季节性。发生雷击时，雷电通道周围会产生强烈的电磁辐射场，当雷击发生在海面上的时候，会对水下工作的电磁场传感器以及水中兵器产生影响[2]。由于海水对高频电磁波具有强烈的吸收作用，雷电产生的海洋电磁场能量主要集中在极低频。

使用经典算法进行信号谱估计时，为获得必需的频率分辨率需要记录较长的数据，同时，由于加窗必然存在功率泄露和频率混叠使接受的弱信号被掩盖。近代谱估计就是为了克服以上缺点而提出的，它的基本思想是对所观察的有限数据以外的数据不作任何确定性假设。在一定先验知识的基础上，采用外推或预测的方法，从观测的数据中推导以后的数据[3]。由于雷电现象持续的时间较短，能量又主要集中在极低频，属于短数据记录。利用传统的谱估计方法难以克服频率分辨率低和谱泄露的缺点，因此，为了解决这些问题，在处理雷电短记录数据时引入了现代谱估计技术。

1 Levinson-Durbin算法

以AR模型为基础的现代谱估计，需要知道模型的阶和AR 系数，以及模型激励源的方差。为此，必须把这些参数和已知的自相关函数联系起来，这就是著名的Yule-Walker 方程。用线性方程组的常用解法求解Yule-Walker 方程，需要的运算量较大，但若利用系数矩阵的对称性和Toeplitz性质，则可构成一些高效算法。Levinson-Durbin（简称L-D）算法是其中最著名、应用最广泛的一种[4]。

L-D算法的运算步骤如下：

2 仿真信号的比较

由于雷电为短暂的脉动形式，并且海水对高频电磁波的衰减较快。雷电产生的海洋电磁场能量主要集中在10 Hz以下的极低频，信号的时间长度甚至不足1个周期。由于传统的谱估计方法对短记录数据的频率分辨率较低，会出现严重的谱泄漏现象，从而导致估计的线谱频率不准，而L-D 算法甚至可以从部分周期中提取出线谱信息，但FFT 如果没有几个周期就无法做到这一点[6]。

为了比较研究FFT 与L-D 算法的性能，首先将其应用在仿真信号中。仿真信号的频率为5 Hz，利用 MATLAB 软件进行绘图，得到 0.5T，0.9T，2.5T 及4T 的频谱图（T 为信号1 个周期的长度）。为了方便比较，对频谱分析结果进行了归一化处理，得到的频谱如图1所示。

从图1 中可以看出，当信号不足1 个周期时，经FFT 得到的分析结果线谱较宽，无法准确判断信号频率；L-D 算法的频谱结果表明，当信号记录不足1个周期时（如图1b 所示）就可以提取出线谱频率。随着信号周期的增加，FFT的线谱特性越来越明显，但与L-D算法分析结果相比，其线谱仍较宽。

3 实测数据的比较

利用大连测控技术研究所自主研制的海洋环境电磁场观测系统，多次采集到海面雷电现象。下面以一次雷电产生的垂直分量电磁场为例，比较分析FFT与L-D算法的应用结果。雷电产生的电磁场时域信号如图2所示，数据截取的时间长度为1 s，雷电信号的持续时间约为0.5 s。

以参数模型为基础的谱估计方法一般按下列3个步骤进行。

1）为被估计的随机过程确定或选择一个合理的模型，文中选择的是AR模型。

2）根据已知观测数据估计模型参数。

3）用估计得到的模型参数计算功率谱[4]。

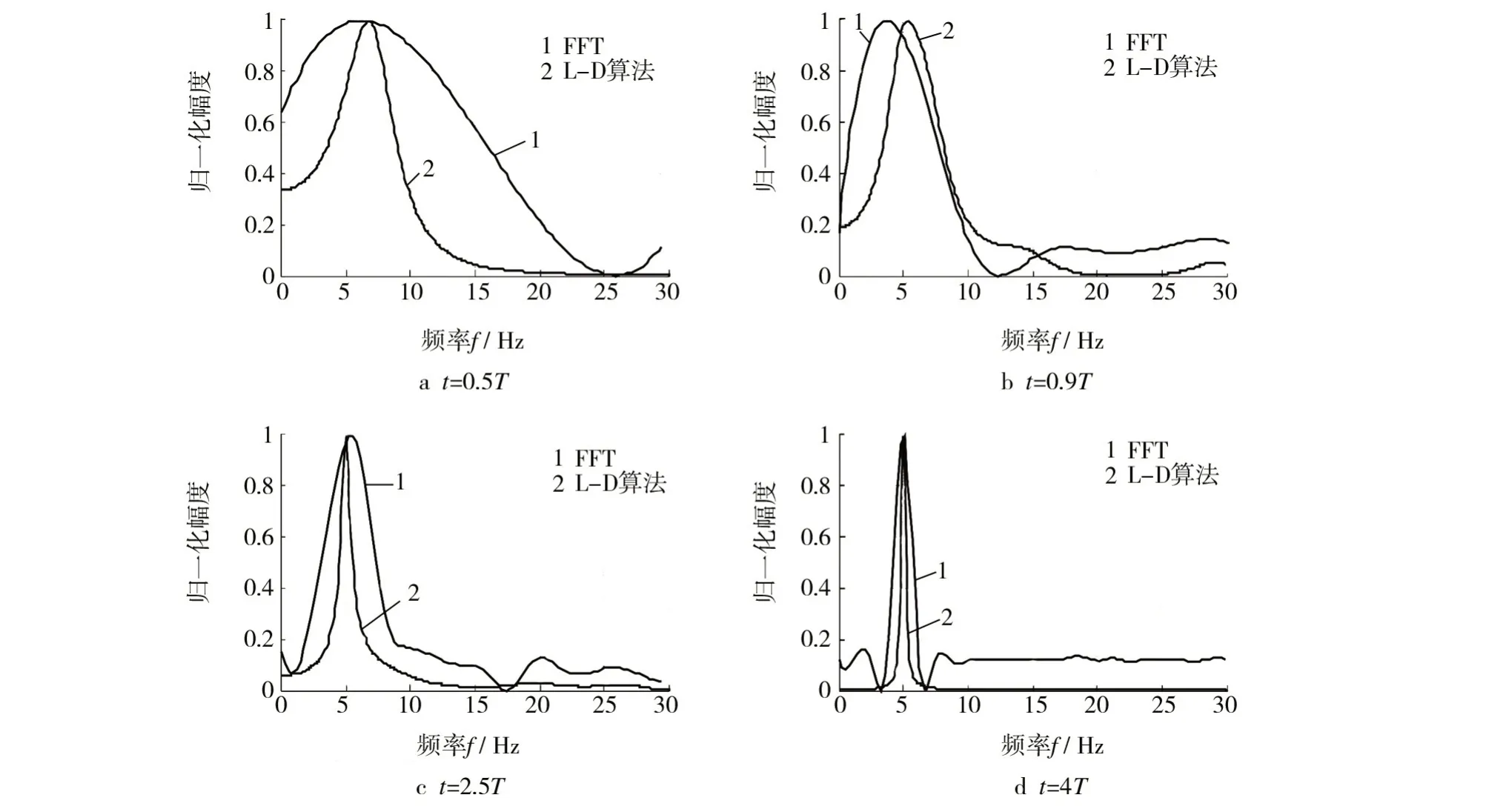
图1 不同时间长度的频谱Fig.1 Spectrum of different time length

图2 雷电产生的电磁场时域波形Fig. 2 Time domain waveform of electromagnetic field in sea generated by lightning

采用AR 模型谱估计方法，既要估计AR 模型参数，又要估计模型的阶。文中以最终预测误差（FPE）准则和Akaike 信息准则（AIC）结合实测数据进行讨论。

FPE准则函数：

AIC准则函数：

图3 FPE与模型阶的关系曲线Fig.3 The relationship between FPE and order

图4 AIC与模型阶的关系曲线Fig.4 The relationship between AIC and order

根据模型阶数和L-D 递推算法得到的AR 模型参数可以估计信号的功率谱。为了方便研究，对功率谱进行了幅度归一化，得到各自的频谱如图5、图6所示。

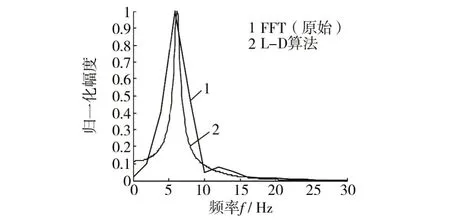
图5 FFT直接输出结果和L-D算法比较Fig.5 Comparison between FFT（primary）and L-D

图6 FFT插值后和L-D算法比较Fig.6 Comparison between FFT（interpolation）and L-D

由分析处理结果可知：L-D 算法具有明显的线谱特性，线谱较窄，检测出的信号频率为6.2 Hz；FFT的线谱较宽，线谱分辨率低，线谱特性不明显，检测出的信号频率在5.9 Hz附近。

4 结语

针对雷电产生的海洋电磁场记录时间短的特点，研究了仿真信号FFT 与L-D 算法的频谱分析结果。结果表明，L-D算法利用不足1个周期的数据便可以准确提取出信号的线谱频率；FFT 在数据量不足几个周期时，其频谱分辨率仍然较低，无法得到确切的线谱频率信息。基于仿真信号的研究，选择AR模型作为雷电随机过程的模型。结合FPE和AIC准则确定AR 模型阶数，利用L-D 算法求取AR 模型参数，从而计算出其功率谱。对雷电实测数据的处理结果达到了预期效果，体现了L-D算法的应用价值。

利用现代谱估计技术准确识别雷电环境，可以为海军装备设计、研制提供参考，而且也是合理使用、充分发挥武器装备性能的基础信息。

[1]李楠，张雪飞.战场复杂电磁环境构成分析[J].装备环境工程，2008，5（1）：16—19.

[2]李松，龚沈光.空气-海水两层模型中雷电在海水中产生的电磁场计算[J].海军工程大学学报，2008，20（6）：40—44.

[3]刘茵，李诚人. 自回归滤波器的研究[J]. 计算机仿真，2006，23（6）：107—108.

[4]姚天任，孙洪.现代数字信号处理[M].武汉：华中科技大学出版社，1996：123—131.

[5]张永春，王明江.线性预测编码中Levinson-Durbin 算法的ASIC实现[J].计算机与数字工程，2005，33（9）：118—119.

[6]IAN B Murray，ALASTAIR D McAulay. Magnetic Detection and Localization Using Multichannel Levinson-Durbin Algorithm[J]. Proceedings of SPIE，2004：561—566.（余不详）

[7]陈国强，赵俊伟，黄俊杰，等.基于Matlab的AR模型参数估计[J].工具技术，2005，39（4）：39—40.