一种可有效分割小目标图像的阈值选取方法
2011-02-21吴一全吴加明占必超
吴一全,吴加明,占必超
(1.南京航空航天大学电子信息工程学院,江苏南京210016;2.南京大学 计算机软件新技术国家重点实验室,江苏 南京210093)
阈值分割是使用普遍、处理有效且实现简单的图像分割技术。其关键是快速选取合适的阈值以实现准确分割。国内外学者对此进行了大量研究[1-2],提出了基于最大类间方差(Otsu 法)[3]、最大熵[4]、Fisher 准则[5]等多种类型阈值选取方法。最初都通过图像的一维灰度直方图选取阈值,虽然处理速度快,但图像受到噪声干扰时难以获得满意的分割效果。因此,最大熵法、Otsu 法和Fisher 准则法分别被Abutaleb[6]和Brink[7]、刘健庄[8]、龚坚[9]等相继推广到灰度级—邻域平均灰度级二维直方图,效果明显改善,但同时运算量按指数增加。故人们又提出了基于二维直方图的阈值选取快速算法[10-12],不同程度地提高了运行速度。但上述二维方法都将二维直方图分成4 个矩形区域(称之为区域直分),而这样会在计算中引入近似,导致分割结果不够准确。因此,文献[13 -15]提出了基于二维直方图区域斜分的阈值分割方法,进一步减小了误差,大大缩短了运行时间,且抗噪性更稳健。
图像阈值分割是红外目标检测中的关键步骤之一。在红外目标探测成像平面内,目标与背景的大小之比通常很小,如低于1%.这就要解决目标与背景大小之比很小的小目标图像阈值分割问题。对于这一问题,现有的阈值选取方法几乎都失效,得不到理想结果。当目标与背景比例相差较大时,将背景的一部分划分为目标反而可能具有更小的类内方差或更大的类间方差。因此,Otsu 法和Fisher 准则法不能准确地分割小目标图像; 最大熵方法对小目标图像也不能有效分割。
鉴于以上原因,本文提出了一种基于背景与目标面积差和类内方差的小目标图像分割阈值选取方法。考虑到准确分割时,目标内部和背景内部的灰度均匀,类内方差很小,再利用小目标图像中目标与背景的面积相差很大的特点,构造准则函数;在此基础上,分别给出了基于一维直方图和二维直方图区域直分的阈值选取公式; 然后导出了二维直方图区域斜分阈值选取公式及其快速递推算法; 最后在实验结果中,给出了本文方法的阈值分割结果和运行时间,并与基于二维斜分的Otsu、最大熵及Fisher 阈值选取快速方法进行了比较。
1 基于一维直方图和二维直方图区域直分的阈值选取
1.1 基于一维直方图的阈值选取
Otsu 法根据最大类间方差或最小类内方差选取阈值,实质上是基于误差平方和最小准则导出的。该准则有一个潜在的问题,即当不同聚类所包含的样本个数相差较大时,将一个大的类别分割开反而可能具有更小的误差平方和。对于小目标图像,目标与背景所占比例相差较大,将背景的一部分划分为目标反而可能具有更小的类内方差或更大的类间方差,因此Otsu 法将不能准确分割。
考虑到准确分割时,目标内部和背景内部的灰度均匀,数据点紧密,类内方差很小; 如果再利用小目标图像的目标与背景的面积比例很小也即目标与背景的面积相差很大的特点,将其考虑为阈值选取准则函数的一部分,可望提高阈值分割的准确性。综合上述2 个特点,本文构造了基于背景与目标的面积差和类内方差的阈值选取准则函数,从而可有效地分割小目标图像。
设图像的尺寸为M×N,灰度级取0,1,…,L -1,p(i)为灰度级i 出现的概率。现用阈值t 划分为背景类和目标类,假设图像的亮(暗)像素属于目标(背景)。背景和目标的概率分别为ω0(t)、ω1(t),灰度级均值分别为μ0(t)/ω0(t)、μ1(t)/ω1(t),方差分别为σ20(t)、σ21(t).该准则函数的一维形式为
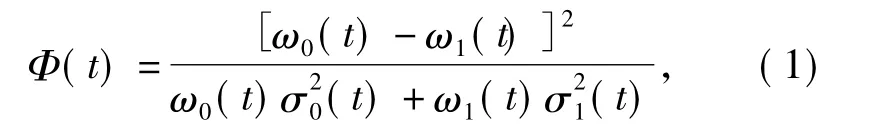
使准则函数Φ(t)达到最大求得最佳阈值:
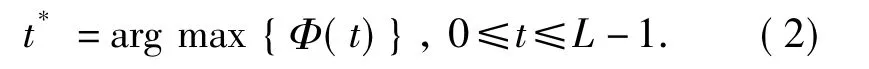
1.2 基于二维直方图区域直分的阈值选取
设M×N 图像的灰度级取0,1,…,L -1,定义像素点(m,n)的邻域平均灰度级g(m,n)=,其中D 一般取像素点(m,n)的3 ×3邻域,W 为D 中的像素点数。若用r(i,j)表示(灰度级f,邻域平均灰度级g)对出现的频数(0 ≤r(i,j)≤M×N),定义:
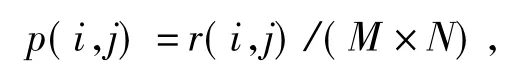
则p(i,j)即为图像的二维直方图。图1(a)为原始图像,图1(b)为其二维直方图,阈值向量(t,s)将二维直方图直分为图1(c)所示的4 个区域。
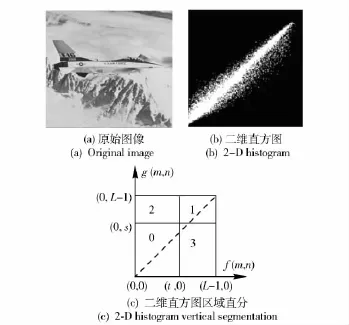
图1 图像二维直方图及其区域直分Fig.1 2-D histogram and vertical segmentation
设背景和目标的概率分别为ω0(t,s)、ω1(t,s),灰度级均值分别为μ0i(t,s)/ω0(t,s)、μ0j(t,s)/ω0(t,s)、μ1i(t,s)/ω1(t,s)、μ1j(t,s)/ω1(t,s),方差分别为σ20i(t,s)、σ20j(t,s)、σ21i(t,s)、σ21j(t,s),则由一维形式推广,得到基于背景与目标面积差和类内方差的二维直分阈值选取准则函数
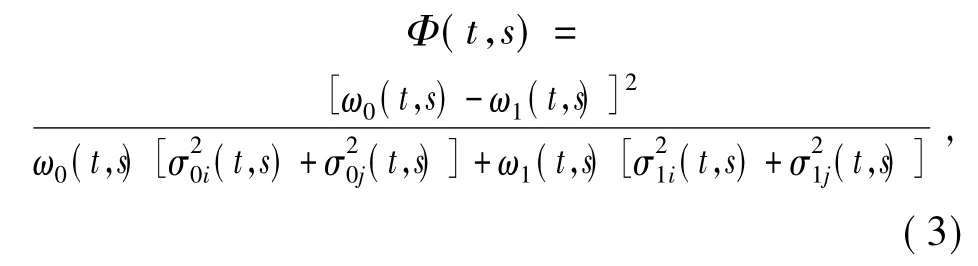
使准则函数Φ(t,s)达到最大求得最佳阈值:
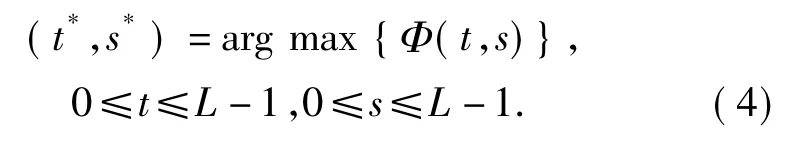
此时,分割后的图像类内均匀,目标与背景分离度最佳。
2 二维直方图区域斜分的阈值选取公式及其快速递推算法
2.1 二维直方图区域斜分的阈值选取公式
分析图1(b)所示的二维直方图可见,像素点基本都分布在主对角线附近,故在图2中,通过位于主对角线两侧且与其平行的4 条平行斜线L1、L2、L3、L4,将直方图区域分成1 个内点区、2 个边界点区和2 个噪声点区:L1 和L2 之间的区域由于像素灰度级和邻域平均灰度级相近,认为是目标和背景内点区;L1 和L3 之间及L2 和L4 之间的2 个区域因像素灰度级和邻域平均灰度级有一定差别,视为目标和背景之间过渡的边界点区; L3 以外和L4 以外的2 个区域由于像素灰度级和邻域平均灰度级相差很大,定为噪声点区[14-15]。
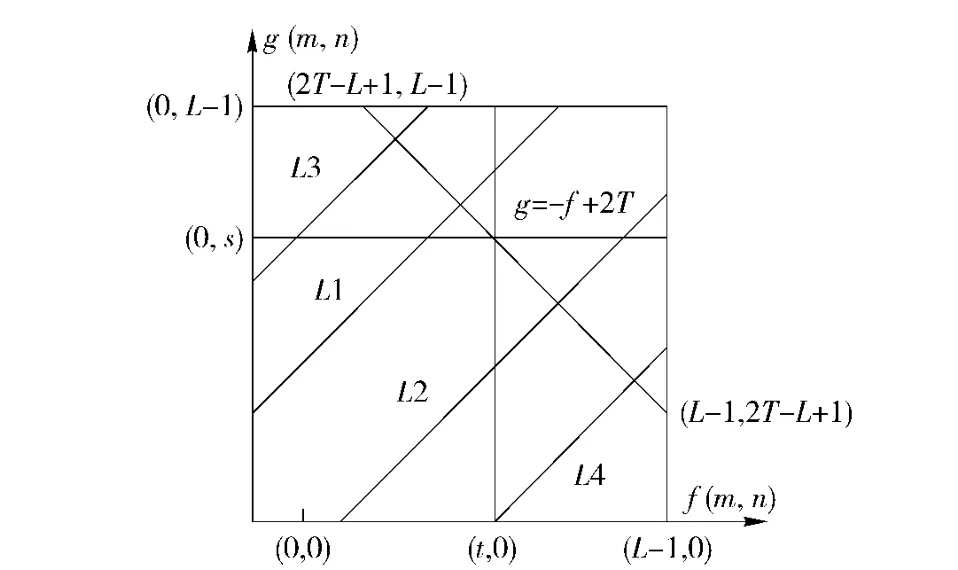
图2 二维直方图区域斜分Fig.2 2-D histogram oblique segmentation
斜分是采用与主对角线垂直(即与灰度级轴成135°角)的一条斜线段g=-f +2T(T 为阈值,0≤T≤L-1),按灰度级与邻域平均灰度级的平均值进行阈值分割,即分割后的二值图像b(m,n)为
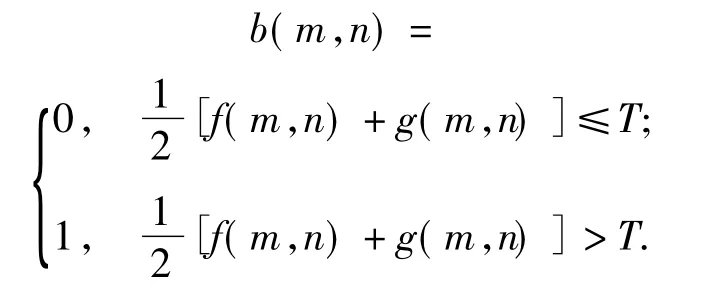
其中,0<T≤L-1.
若背景与目标的概率分别为ω0(T)、ω1(T),灰度均值分别为μ0i(t,s)/ω0(t,s)、μ0j(t,s)/ω0(t,s)、μ1i(t,s)/ω1(t,s)、μ1j(t,s)/ω1(t,s),方差分别为σ2oi(T)、σ2oj(T)、σ21i(T)、σ21j(T),则基于背景与目标面积差和类内方差的二维斜分阈值选取准则函数为
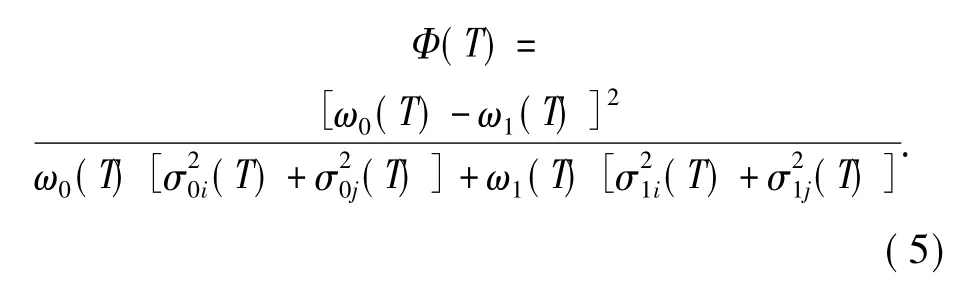
若设总体灰度级均值为μti和μtj,总体方差σ2为σ2ti和σ2tj,由于斜分情况下总体方差为类内方差与类间方差之和,所以(5)式的准则函数可改写为
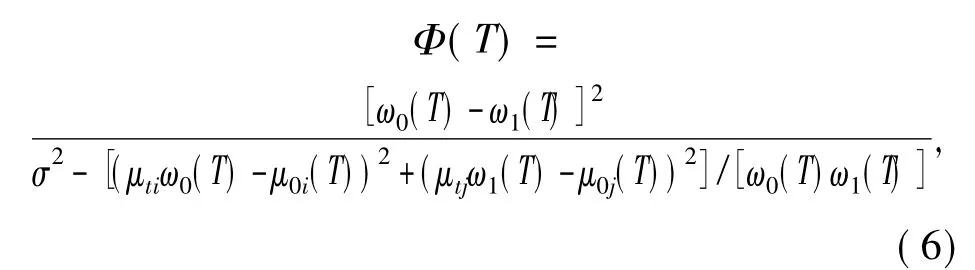
使准则函数Φ(T)达到最大求得最佳阈值:
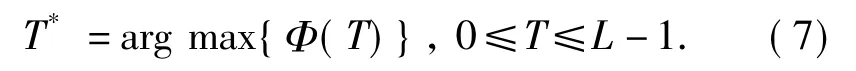
2.2 快速递推算法
从上述算法公式可以看出,计算Φ(T)需要计算ω0(T)和ω1(T)、μ0i(T)和μ0j(T)、μti和μtj、σ2ti和对于同一幅图像,μti和μtj、σ2ti和σ2tj是固定的。对于每一个阈值T,如果每次计算Φ(T)都重新从i=0,j=0 开始累加计算ω0(T)、μ0i(T)、μ0j(T),势必造成大量的重复计算,而且计算复杂性都为o(L2),而共有L-1 个阈值T,从而使总的计算复杂性达到o(L3).
0<T≤L/2 -1 时,递推公式推导如下:
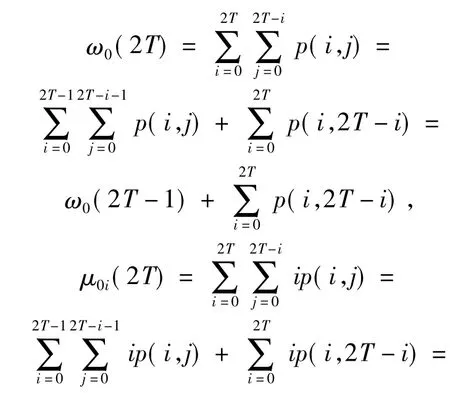
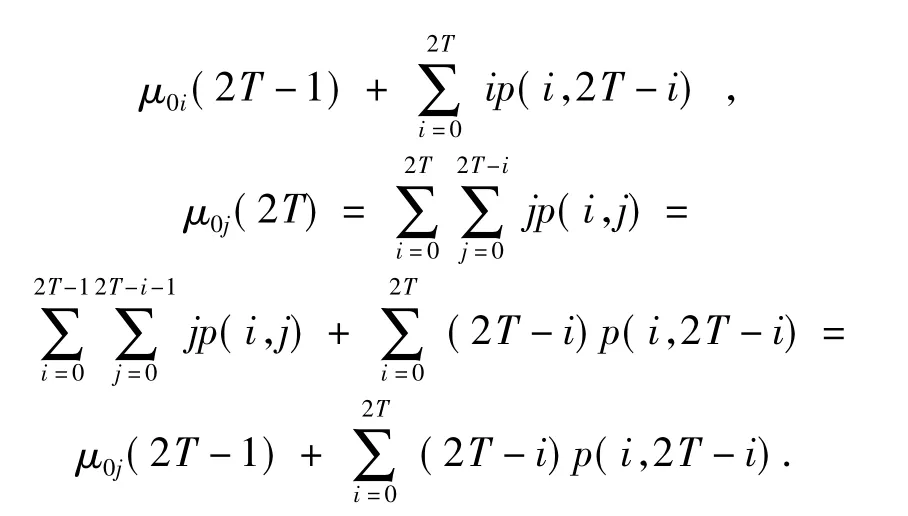
同理可以得到L/2≤T≤L-1 时的递推公式。
根据上述递推公式,每计算一次Φ(T)都勿需重新计算ω0(2T)、μ0i(2T)、μ0j(2T),只要分别利用前面得到的ω0(2T -1)、μ0i(2T -1)、μ0j(2T -1),再加上直线段g=-f +2T 上各点相应的值即可。这样就只要分别在T =0,1,…,L -1 范围内搜索。计算μ0i、μ0j需要次乘法,而对于每一个T,计算准则函数需要8 次乘法,所以总的计算复杂性为2L2+16L~o(L2).而发现对于ω0(2T)、μ0i(2T)、μ0j(2T)及ω0(2T-1)、μ0i(2T-1)、μ0j(2T -1)可以只用3 个存储单元来存储,而不用把对应每个T 的值都存起来,只要在累加时往上加即可,大大减少了存储空间。
上述算法流程图如图3所示。
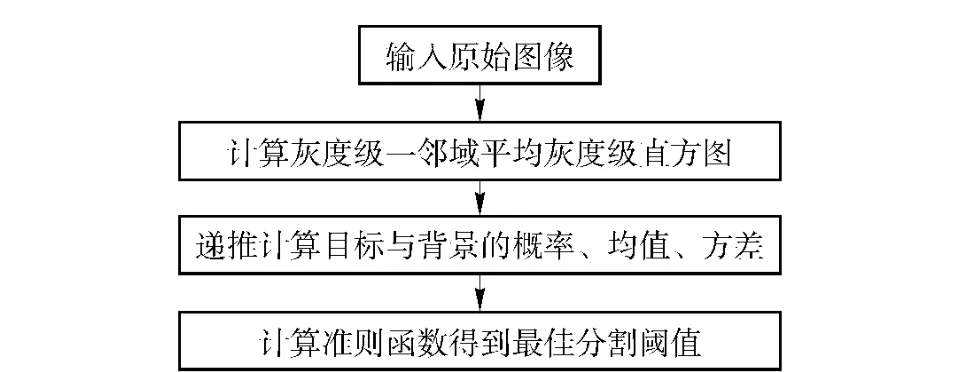
图3 算法流程图Fig.3 Flowchart of the algorithm
3 实验结果和分析
3.1 基于一维直方图、二维直方图区域直分以及斜分的本文方法比较
本文进行了大量实验,现举一例说明。图4分别给出了基于一维直方图、二维直方图区域直分以及斜分的本文方法对同一幅舰船图像进行阈值分割的结果。其中图4(a)为原始舰船图像,大小为155 像素×154 像素,图4(b)为基于一维直方图的分割结果,图4(c)为基于二维直方图区域直分的分割结果,图4(d)为基于二维直方图区域斜分的分割结果。可以看出,本文方法不仅能够准确地提取目标,而且二维方法的抗噪性较好,特别是基于二维直方图斜分方法的抗噪性更为稳健。
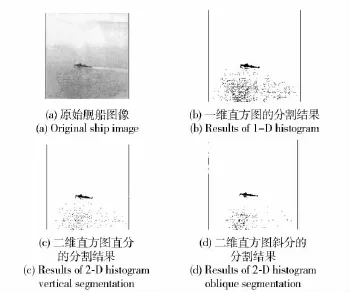
图4 本文方法的分割结果Fig.4 Segmentation results of different methods

表1 4 种方法的分割结果Tab.1 Segmentation results of four methods
3.2 与其它方法的比较
针对200 多幅各类较小目标图像进行了实验。现选取其中5 幅图像加以说明。其中目标都是飞行器,但其与红外成像平面的远近距离不同。下面分别给出本文方法与基于二维直方图区域斜分的Otsu法、最大熵方法、Fisher 准则法的分割结果。如表1所示,从上到下分别为图像1~图像5,每一行从左到右依次为原始图像、一维直方图及Otsu 方法、最大熵方法、Fisher 方法、本文方法的分割结果。图像1的大小为322 像素×221 像素,目标与背景大小比例为6.8%,虽然4 种方法都能将目标分割出来,但本文方法去噪性更好;图像2、图像3 的大小分别为323 像素×217 像素和256 像素×256 像素,目标与背景大小比例分别为4.2% 和3.9%,Otsu 法和Fisher 方法此时已不能有效分割,最大熵方法虽然能分割出来,但仍存在噪声;图像4 的大小为104 像素×90 像素,目标与背景大小比例为0.43%,此时Otsu 法和Fisher 方法已基本失效,最大熵方法分割结果的噪声变大,失去准确性,而唯有本文方法能较准确地将小目标分割出来,相对其它分割方法,其噪声已达最小,且分割结果满足要求; 图像5 的大小为106 像素×94 像素,目标与背景大小比例为0.18%,分割效果与图像4 类似,进一步体现了本文方法分割小目标图像的优越性。
实验是在Intel Pentium 4 CPU 2.80 GHz/512 MB 内存/Matlab 7.1 的计算机环境中进行的。表1中4 种方法的分割阈值及运行时间如表2所示,表2中的百分比表示目标与背景大小比例。
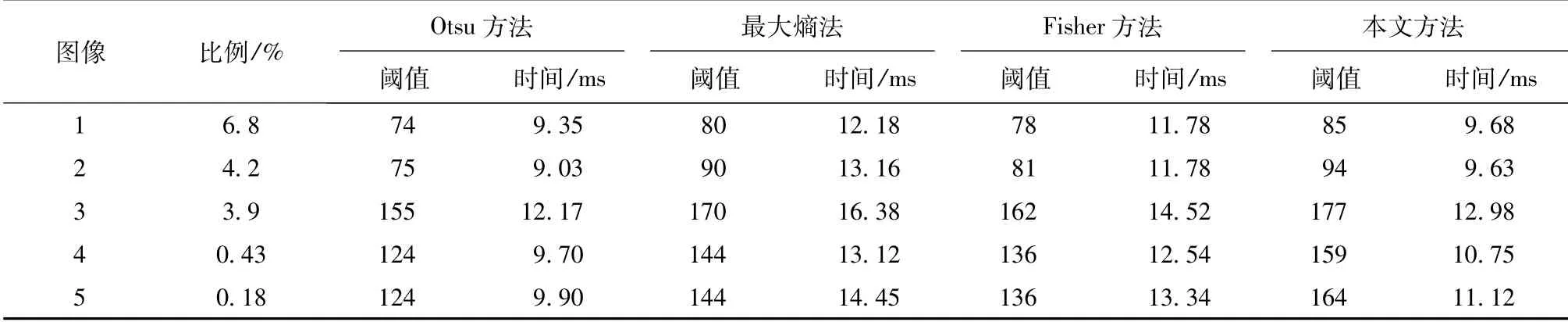
表2 4 种方法的阈值及运行时间Tab.2 Threshold and running time of four methods
从表2中可以看出,对于每幅图像,Otsu 方法的运行时间最短,但其在小目标图像分割中,效果最差;最大熵方法分割效果优于Otsu 方法,但因涉及对数运算其运行时间最长; Fisher 方法分割效果略好于Otsu 方法,但仍然较差,而且运行时间也比Otsu方法长;本文方法分割效果最佳,能准确地分割出小目标,运行时间仅比Otsu 方法稍长,少于Fisher方法和最大熵方法。
4 结论
本文提出的基于背景与目标面积差和类内方差的图像分割阈值选取方法,可有效地分割目标与背景大小之比很小的小目标图像。大量实验结果表明:该方法能使分割后图像中的目标和背景区域内部均匀,边界形状准确;基于二维斜分方法的抗噪性优于一维和二维直分方法; 所用的二维直方图区域斜分快速递推算法,降低了二维空间搜索的代价,大大提高了运行速度; 与目前性能较优越的基于二维斜分的Otsu、最大熵及Fisher 准则图像分割阈值选取快速方法相比,本文方法在小目标图像分割效果上具有极为明显的优势。
References)
[1]吴一全,朱兆达.图像处理中阈值选取方法30年(1962—1992)的进展(一)[J].数据采集与处理,1993,8(3): 193 -201.WU Yi-quan,ZHU Zhao-da.30 years (1962—1992)of the developments in the threshold selection methods in image processing(Ⅰ)[J].Journal of Data Acquisition & Processing,1993,8(3):193 -201.(in Chinese)
[2]吴一全,朱兆达.图像处理中阈值选取方法30年(1962—1992)的进展(二)[J].数据采集与处理,1993,8(4): 268 -282.WU Yi-Quan,ZHU Zhao-da.30 years(1962—1992)of the developments in the threshold selection methods in image processing(Ⅱ)[J].Journal of Data Acquisition & Processing,1993,8(4):268 -282.(in Chinese)
[3]Otsu N.A threshold selection method from gray-level histogram[J].IEEE Transactions System Man and Cybernetics,1979,9(1):62 -66.
[4]Kapur J N,Sahoo P K,Wong A K C.A new method for grey-level picture thresholding using the entropy of the histogram[J].Computer Vision,Graphics and Image Processing,1985,29(1): 273-285.
[5]陈果.图像阈值分割的Fisher 准则函数法[J].仪器仪表学报,2003,24(6):564 -567.CHEN Guo.The Fisher criterion function method of image thresholding[J].Chinese Journal of Scientific Instrument,2003,24(6):564 -567.(in Chinese)
[6]Abutaleb A S.Automatic thresholding of gray-level picture using two-dimensional entropies[J].Pattern Recognition,1989,47(1):22 -32.
[7]Brink A D.Thresholding of digital image using two-dimensional entropies[J].Pattern Recognition,1992,25(8):803 -808.
[8]刘健庄,栗文青.灰度图像的二维Otsu 自动阈值分割法[J].自动化学报,1993,19(1):101 -105.LIU Jian-zhuang,LI Wen-qing.Automatic thresholding using the Otsu algorithm based on the two-dimensional gray image[J].Acta Automatica Sinica,1993,19(1):101 - 105.(in Chinese)
[9]龚坚,李立源,陈维南.基于二维灰度直方图Fisher 线性分割的图像分割方法[J].模式识别与人工智能,1997,10(1):1 -8.GONG Jian,LI Li-yuan,CHEN Wei-nan.The gray-level thresholding method based on Fisher linear discriminant of two-dimensional histogram[J].Pattern Recognition and Artificial Intelligence,1997,10(1):1 -8.(in Chinese)
[10]Gong J,Li L Y,Chen W N.Fast recursive algorithms for two-dimensional thresholding[J].Pattern Recognition,1998,31(3):295 -300.
[11]景晓军,蔡安妮,孙景鳌.一种基于二维最大类间方差的图像分割算法[J].通信学报,2001,22(4):71 -76.JING Xiao-jun,CAI An-ni,SUN Jing-ao.Image segmentation based on 2D maximum between-cluster variance[J].Journal of China Institute of Communications,2001,22(4):71 -76.(in Chinese)
[12]汪海洋,潘德炉,夏德深.二维Otsu 自适应阈值选取算法的快速实现[J].自动化学报,2007,33(9):968 -971.WANG Hai-yang,PAN De-lu,XIA De-shen.A fast algorithm for two-dimensional Otsu adaptive threshold algorithm[J].Acta Automatica Sinica,2007,33(9):968 -971.(in Chinese)
[13]范九伦,赵凤.灰度图像的二维Otsu 曲线阈值分割法[J].电子学报,2007,35(4):751 -755.FAN Jiu-lun,ZHAO Feng.Two-dimensional Otsu curve thresholding segmentation method for gray-level images[J].Acta Automatica Sinica,2007,35(4):751 -755.(in Chinese)
[14]吴一全,潘喆,吴文怡.二维直方图区域斜分阈值分割及快速递推算法[J].通信学报,2008,29(4):77 -83.WU Yi-quan,PAN Zhe,WU Wen-yi.Image thresholding based on two-dimensional histogram oblique segmentation and its fast recurring algorithm[J].Journal of China Institute of Communications,2008,29(4):77 -83.(in Chinese)
[15]吴一全,潘喆,吴文怡.二维直方图区域斜分的最大熵阈值分割算法[J].模式识别与人工智能,2009,22(1): 162 -168.WU Yi-quan,PAN Zhe,WU Wen-yi.Maximum entropy thresholding algorithm based on two-dimensional histogram oblique segmentation[J].Pattern Recognition and Artificial Intelligence,2009,22(1):162 -168.(in Chinese)
