考虑惯性效应的移动弹丸作用下身管振动特性
2011-02-21史跃东王德石
史跃东,王德石
(海军工程大学 兵器工程系,湖北 武汉430033)
火炮射击过程中,身管的加工缺陷和自重弯曲、布尔登效应、移动弹丸的重力和偏心力、膛内的旋转摩擦力矩等[1]诸多因素均会影响射击精度。其中弹丸膛内高速运动下的重力和偏心力是激发身管振动的一个主要因素,同时,火炮新型发射原理的诞生,也对弹丸运动冲击引起的振动产生了研究需求。在高速弹丸的运动激励下,将产生运动与身管振动的耦合,这种耦合在常规出口速度的条件下,往往不被重视,而新型电磁炮发射架的总体设计中,由于弹丸出口速度的提高,弹丸膛内高速运动将引起发射架的何种振动就成为需要研究的理论问题。高速运动弹丸有可能成为影响火炮射击精度的重要因素。因此,有必要对弹丸膛内运动引起的身管振动的动力学过程进行研究。
对于此类问题的研究,早期主要存在于铁路、桥梁和机械工程领域,其讨论的重点为移动质量载荷作用下梁的动力响应[2-4]。在国内,叶开沅等[5]针对列车过桥问题,建立了任意单个移动激励作用下铁路桥梁的动力学方程,并采用小参数法给出了方程的一般解; 姜沐[6]采用Picard 迭代法对文献[5]中方程进行了重新求解,在应用上更具广泛性,且简明易用。周叮[7]和康新中等[8]将该类分析方法应用于火炮振动领域,研究了弹丸膛内运动引起的火炮身管横向振动问题,但只进行了定性分析,没有进行定量计算;在忽略移动载荷惯性效应的前提下,姜沐[9]进一步建立了加速弹丸作用下火炮身管横向振动方程,给出了级数形式的解析解和定量计算结果。到目前为止,在火炮振动研究领域内,关于这方面的研究工作还较少,理论分析与定量计算也不多。
在以往该类研究的基础上,建立了弹丸膛内高速运动下计及其惯性效应的火炮身管横向振动方程,采用小参数法给出了方程级数形式的解析解,讨论了弹丸有、无质偏2 种工况下的身管振动特性,分析了不同运动参数对炮口振动的影响规律,给出了定量比较结果,并在此基础上进一步研究了连发射击下的炮口振动响应,得到的结论可为火炮与弹药的总体设计、结构优化提供技术基础。
1 移动弹丸作用下身管横向振动方程
将身管简化为一端固定另一端自由的欧拉均匀等截面悬臂梁,假定弹丸沿炮膛轴线运动,力学模型如图1所示。图1中:m 为弹丸质量;α 为射角;l 为身管长度;v 为弹丸膛内运动平均速度;y(x,t)为身管在坐标(x,0)处的挠度; F(t)为不计惯性效应时弹丸膛内运动作用于身管上的等效合外力。
设身管的抗弯刚度为EI,质量为M,取纵坐标Oy,横坐标Ox,在计及阻尼和弹丸惯性效应时,移动弹丸作用下身管横向振动方程(Oy 方向为正向)
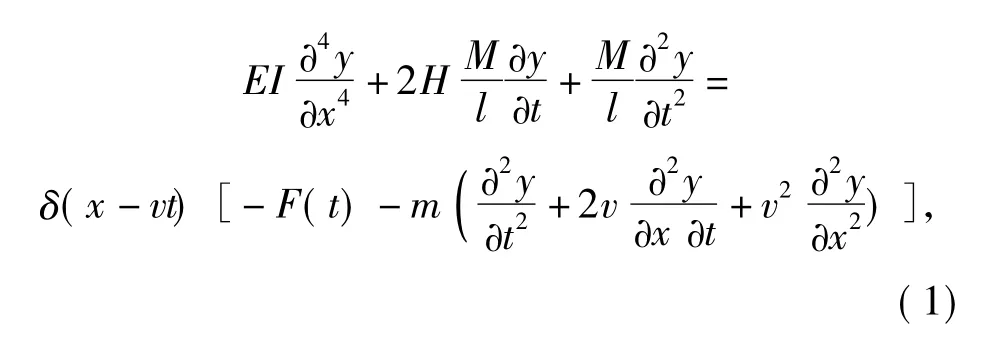
式中:H 为阻尼衰减系数; δ(x - vt)为Dirac 函数;为计及弹丸惯性效应后作用于身管上的外力附加项。(1)式的边界条件和初始条件分别为

欲使上述方程更具一般性,进行无量纲化处理,引入下列无量纲变量

则(1)式~(3)式的无量纲形式分别为

鉴于ε≪0.5,选其为小参数,在边界条件(6)式和初始条件(7)式下,用小参数法[10](5)式。将(5)式的解w 展成如下形式的ε 的升幂级数

式中:w0,w1,w2,…为含x',t'的待定函数。将(8)式代入(5)式~(7)式中,同时将ε 因次相同的项合并在一起,可得一系列关于w0,w1,w2,…及相应边界条件、初始条件的微分方程。
对于w0,有如下方程,边界条件和初始条件

令w0的解为
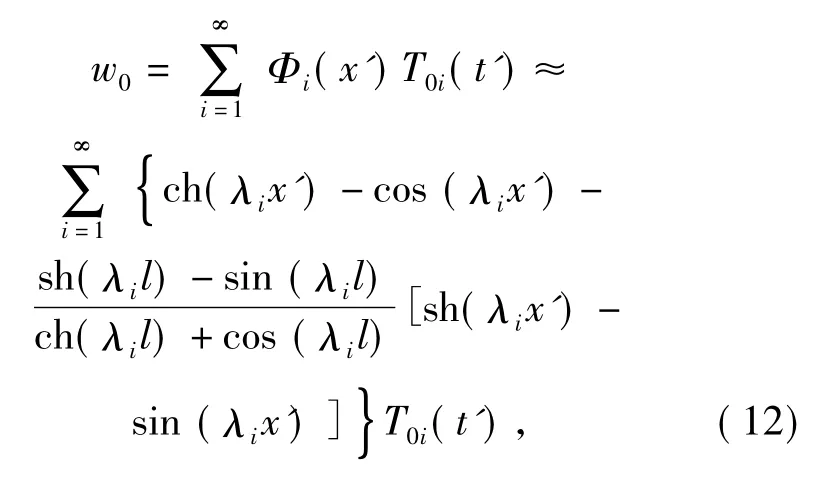
式中:λi=(i-0.5)π;Φi(x')为满足边界条件(10)式的悬臂梁振型函数。将(12)式代入(9)式,两端乘以Φi(x'),然后由0 到1 对x'积分,得

其中

将(12)式代入(11)式,即得对应于w0的初始条件

在初始条件(14)式下,由Duhamel 积分解(13)式可得

因此(9)式的解可写为

对于w1,有如下方程,边界条件和初始条件


令w1的解为

将(16)式、(20)式代入(17)式,进行和前面过程一样的处理,得如下方程和初始条件

式中
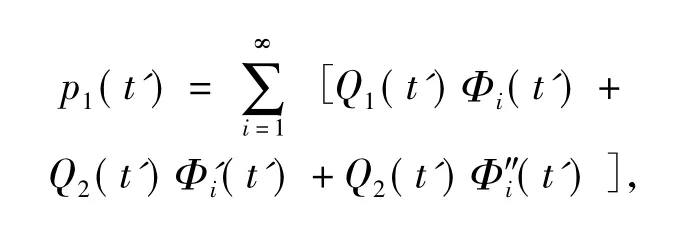
这里

在初始条件(22)式下,解(21)式得

对于w2,w3,…,可按同样思路求解,将其全部代入(8)式,即可得w 级数形式的解析表达式。
2 振动算例
由于弹丸膛内高速运动具有瞬时冲击性,即使身管发生轻微弯曲,弹丸通过时也会对其产生极大的作用力。这里将弹丸对身管的作用力分为2 种工况进行讨论: 1)弹丸无质偏,2)弹丸有质偏。
2.1 弹丸无质偏
当弹丸无质偏时,(1)式中等效合外力F(t)可简化为移动弹丸自重对身管的作用力,因此有

式中:f(t')为ε 的一次式,故可将其并入(5)式无量纲化处理后的惯性附加项中。此时采用前叙小参数法进行振动方程的求解,易知w 中的w0分量恒为0,只须计算ε 的非0 次项即可,可设
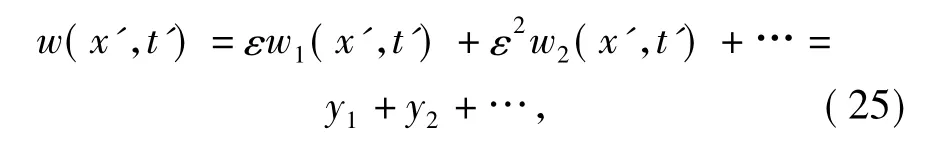
将(24)式~(25)式代入(5)式,整理可得对应于wq,q=1,2,…,的振动方程,这里以w1为例有

式中边界条件、初始条件和解法的处理与前面介绍的完全一致。求得w1后,采用类似方法可迭代求出w 中其余各项,再利用(4)式反解算出y,即可完成问题的最终求解。
对此种工况下推得的解析结果进行了数值仿真,参数选取:m=13.5 kg;v=687.5 m/s;l=5.5 m;α=45°; E =210 GPa; g =9.8 m/s2.仿真结果如图2、图3所示。

图2 炮口振动分量yn(l,t)Fig.2 Component yn(l,t)of muzzle vibration
图2为与w(1,t')相对应的炮口振动幅度y(l,t)的各分量仿真结果。从图2可以看出,y1(l,t)的数值变化范围(10-6m)远大于其余分量(10-7m),因此在y(l,t)的最终数值确定中起主导地位。图3为不同计算精度下y(l,t)的仿真结果,其中实线为计算到(25)式的第3 项,虚线为计算到第5 项。比较图中曲线可发现,2 种情况下的仿真结果一致,误差<1%.实际上,由文献[11]可知,一般情况下,采用小参数法进行本类问题的求解,取小参数解的前3 项便有足够的精度。
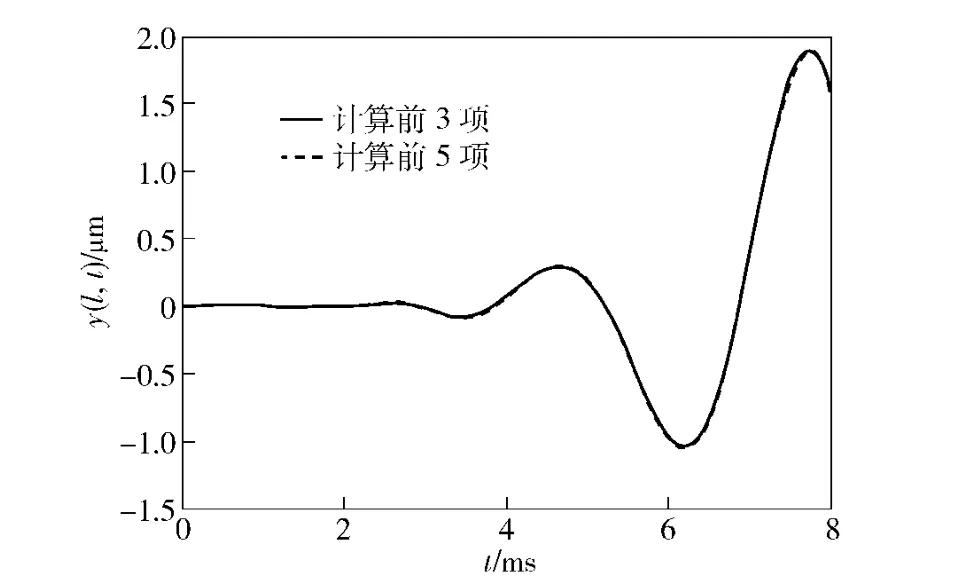
图3 不同计算精度下的炮口振动y(l,t)Fig.3 Muzzle vibration y(l,t)under different calculation precisions
改变弹丸膛内运动速度v,重新进行炮口振动幅度y(l,t)的数值仿真,所得结果如图4所示。从图4中可以看出,随着v 的增大,弹丸飞出炮口阶段(0.7l/v≤t≤l/v)的炮口振动幅度减小; 反之,v 减小,振动幅度增大。
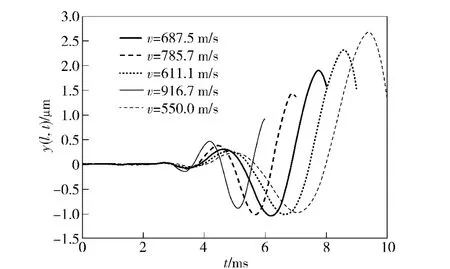
图4 不同运动速度下的炮口振动y(l,t)Fig.4 Muzzle vibration y(l,t)at different projectile velocities
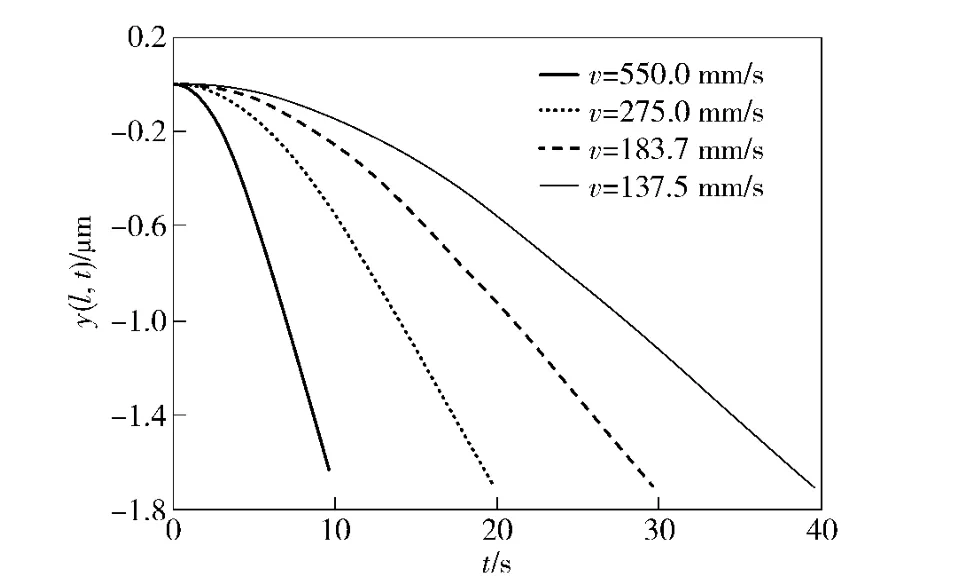
图5 v 趋近于0 时的炮口振动y(l,t)Fig.5 Muzzle vibration y(l,t)when v approaches 0
图5为v 趋近于0 时的炮口振动仿真结果。此时观察弹丸飞出炮口瞬时(t =l/v)的炮口振动幅度y(l,l/v),结果如表1所示。表1中,v=0 时的y(l,l/v)值是在不考虑阻尼和弹丸惯性效应的前提下计算出来的,其值与弹丸直接作用于炮口处的静态形变值相同。比较表中数据可发现,随着v 的不断减小,弹丸飞出炮口瞬时炮口处的振动形态逐渐趋近于弹丸直接作用于炮口处的静变形。

表1 v 趋近于0 时的炮口振动y(l,l/v)Tab.1 Muzzle vibration y(l,l/v)when v approaches 0
图6为v 趋近于∞时的炮口振动仿真结果。与v 趋近于0 时类似,观察弹丸飞出炮口瞬时的炮口振动幅度y(l,l/v),结果如表2所示。随着v 的不断增大,弹丸飞出炮口瞬时炮口处的振动形态逐渐趋近于静止。

图6 v 趋近于∞时的炮口振动y(l,t)Fig.6 Muzzle vibration y(l,t)when v approaches ∞

表2 v 趋近于∞时的炮口振动y(l,l/v)Tab.2 Muzzle vibration y(l,l/v)when v approaches ∞
2.2 弹丸有质偏
弹丸膛内运动时,由于膛线的作用,使得弹丸沿身管轴线方向除作高速平移运动处,还作高速旋转运动。此时弹丸如果存在质偏,其在膛内的高速旋转运动就会产生极大的离心力,从而影响弹丸与身管之间的作用力。反映到(1)式中,F(t)不能再仅简化为弹丸自重对身管的作用力,而应附加考虑弹丸离心力的作用,即

式中:Rs为弹丸质量偏心距;ω 为弹丸膛内转速。对于等齐膛线,由弹道学相关理论知

式中: η 为缠度; d 为身管内径。将(27)式、(28)式代入(24)式,整理有

求得f(t')后,采用与弹丸无质偏时相同的处理方法,即可完成问题的求解。下面重点考察弹丸质量偏心对身管炮口处振动幅度的影响,即仅取f(t')表达式中的第2 项来讨论。参数选取: η =27,Rs=10-4d,其余参数保持不变,仿真结果如图7所示。
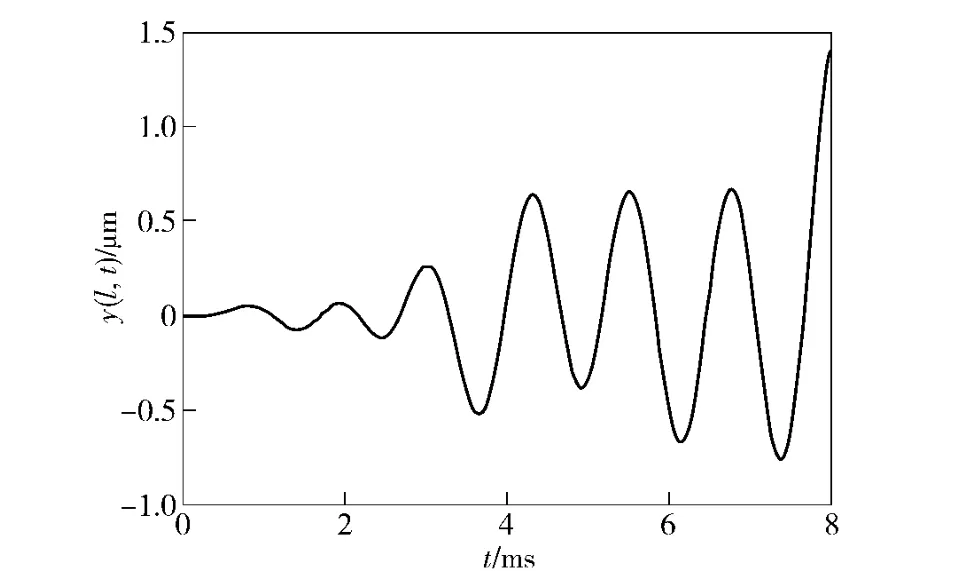
图7 质偏作用下炮口振动y(l,t)Fig.7 Muzzle vibration y(l,t)for mass-unbalance projectile
图7给出了弹丸质偏作用下炮口振动随时间变化的响应曲线,其数值变化范围与图3中相同,都为10-6m.但比较两图后可发现,质偏作用下单次射击周期内的炮口振荡次数明显增多了,这主要是因为F(t)中含有正弦变化量所引起的。
图8为变化弹丸膛内运动速度v 后,质偏作用下炮口振动的仿真曲线。从图8中可看出,随着v的增大,弹丸飞出炮口阶段(0.7l/v≤t≤l/v)的炮口正向振动幅度减小,负向振动幅度增大; 反之,v 减小,则运动规律相反。事实上,由于考虑质偏时F(t)的取值比较复杂,既与弹丸运动速度v 相关,又为t 的周期函数,因此图8中反映出的炮口振动变化规律仅在局部范围(膛内运动时间处于6~10 ms)内成立,对于全局范围内的炮口振动还需进一步分析。取v 趋近于0,重新进行炮口的振动仿真,如图9所示。比较图9中曲线可发现,随着v 的取值大幅度减小,炮口振动幅度亦大幅度减小,并逐渐趋近于0.分析可知,由于v 的取值大幅度减小,势必造成弹丸离心力的大幅度减小,从而导致炮口振幅的快速衰减。同理,亦可对v 趋近于∞时的炮口振动特性进行分析。

图8 不同运动速度下的炮口振动y(l,t)Fig.8 Muzzle vibration y(l,t)at different projectile velocities

图9 v 趋近于0 时的炮口振动y(l,t)Fig.9 Muzzle vibration y(l,t)when v approaches 0
2.3 连发射击
进一步讨论连发射击时移动弹丸激励下身管的横向振动特性。这里以2 连发为例,设第1 发弹丸飞出炮口瞬时,第2 发弹丸恰好进入膛内,则对第2发弹丸激励下的身管有以下初始条件

式中: w*为第2 发射击时的无量纲挠度; tg为无量纲射击间隔; A、B 为第2 发弹丸激励下的身管状态初值,由第1 发弹丸激励下身管的末状态值决定。此时,对应于第2 发弹丸的方程(15)式应改写为

采用类似方式,可改写文中对应于第2 发弹丸的其余方程,并依此进行动力学仿真。参数选取与弹丸无质偏时一致,仿真结果如图10所示。

图10 2 连发射击下的炮口振动Fig.10 Muzzle vibration y(l,t)in burst of fire
由图10可知,连发弹丸激励下的炮口振动幅度数量级为10-5m,远大于单发激励时的10-6m.可见第2 发弹丸激励下的炮口振动受到第1 发的影响,使得炮口振动有增大趋势,即火炮连发射击时的炮口振动幅度远大于单发射击,因此射击精度会有所下降。同时还可发现,连发射击时的炮口振动较为复杂,并不是单发激励下炮口振动的简单重现。同样,可进行多连发射击下炮口振动的动力学仿真。
3 结论
本文基于小参数理论讨论了计及惯性效应的移动弹丸作用下身管横向振动特性,并对弹丸有、无质偏2 种工况下及连发射击下的炮口振动响应进行了较全面的分析,得到主要结论如下:
1)弹丸无质偏时,膛内运动速度v 越大,其飞出炮口阶段的炮口振动幅度越小。对于新型电磁炮而言,虽然弹丸运动速度远大于常规火炮,但对发射架的振动影响不大。
2)弹丸有质偏时,其离心力作用下的炮口振动特性较为复杂,应综合考虑弹丸离心力、自重等因素的影响,合理控制弹丸膛内的运动速度,使得合外力F(t)作用下的炮口振动保持尽量小的幅度。以达到对炮口振动的最佳抑制。
3)建立的动力学方程同样适用于连发弹丸激励下的身管振动求解。连发射击下的炮口振动远大于单发射击,射击精度呈下降趋势。
文中采用的建模方法和小参数解法,亦可应用于移动激励作用下其它相关工程振动问题的求解。下一步工作的研究方向为考虑v 随t 变化的情况,此时方程(5)式中各偏导项系数不再为常量,而为t的函数,问题求解的工作量会有所增大。
References)
[1]奥尔洛夫Б В.炮身构造与设计[M].王天槐,刘淑华,译.北京: 国防工业出版社,1982:157 -167.Орлов Б В.Structure and design for barrel[M].WANG Tianhuai,LIU Shu-hua,translated.Beijing: National Defense Industry Press,1982:157 -167.(in Chinese)
[2]Stokes G G.Discussion of a differential equation relating to the breaking of railway bridges[J].Transactions of the Cambridge Philosophical Society,1982,5: 707 -735.
[3]Timoshenko S P.On the forced vibration of bridges[J].Philosophical Magazine,1922,43(6): 1018 -1019.
[4]Michaltaos G,Sophianopoulos D,Kounadis A N.The effect of a moving mass and other parameters on the dynamic response of a simply supported beam[J].Journal of Sound and Vibration,1996,191(3): 357 -362.
[5]叶开沅,马国琳.计及行动载荷质量及惯性力影响的列车过桥动力理论[J].中国科学A 辑,1984,(4): 338 -352.YE Kai-yuan,MA Guo-lin.Dynamical theory for vehicle-bridge considering moving loads and inertia forces[J].Science in China,1984,(4): 338 -352.(in Chinese)
[6]姜沐.移动质量载荷在梁中激起的振动[J].力学与实践,2002,24(6): 44 -47.JIANG Mu.The dynamic response of a beam under a moving mass[J].Mechanics in Engineering,2002,24(6): 44 - 47.(in Chinese)
[7]周叮,谢玉树.弹丸膛内运动引起炮管振动的小参数法[J].振动与冲击,1999,18(1): 76 -81.ZHOU Ting,XIE Yu-su.The small parameter method for barrel vibration subjected to moving projectile[J].Journal of Vibration and Shock,1999,18(1): 76 -81.(in Chinese)
[8]康新中,吴三灵,马春茂.火炮系统动力学[M].北京: 国防工业出版社,1999: 67 -72.KANG Xin-zhong,WU San-ling,MA Chun-mao.Dynamics of gun system[M].Beijing: National Defense Industry Press,1999:67 -72.(in Chinese)
[9]姜沐,郭锡福.弹丸加速运动在身管中激发的振动[J].弹道学报,2002,14(3): 57 -68.JIANG Mu,GUO Xi-fu.On the vibration of tube due to accelerately moving projectile[J].Journal of Ballistics,2002,14(3):57 -68.(in Chinese)
[10]刘延柱,陈立群.非线性振动[M].北京: 高等教育出版社,2001: 63 -67.LIU Yan-zhu,CHEN Li-qun.Nonlinear vibration[M].Beijing:Higher Education Press,2001: 63 -67.(in Chinese)
[11]奈弗A H.摄动方法[M].上海: 上海科学技术出版社,1983: 10 -21.Nafu A H.Disturbance method[M].Shanghai: Shanghai Technology Press,1983: 10 -21.(in Chinese)
