梁振动问题的拟小波-精细时程积分法

邹 佩， 曲小钢

(西安建筑科技大学理学院, 陕西 西安 710055)

0 引 言

本文采用拟Shannon小波对空间域进行离散，有效的改变了差分法稳定性对步长比的敏感性，并结合精细时程积分法可以长时间精确计算的特点，实现了对梁振动问题高精度、稳定的求解.

1 梁振动方程的拟Shannon小波-精细时程积分法

1.1 拟Shannon小波数值方法

对于混合问题

(1)

采用拟Shannon小波对空间导数进行离散：

(2)

但是正则样本尺度函数不满足正交规范化小波尺度函数的条件，因此，Gauss正则化后的样本尺度函数称为拟尺度函数，由此生成的小波就是拟小波函数.

利用(2)式，f(x)可进一步重构为

(3)

由于拟小波具有良好的局域特性，实际计算时只需要在网格点x附近取2W个计算点.(3)式对于空间坐标的n阶导数为

(4)

(5)

1.2 方程的离散

由于精细时程积分法适宜于关于时间变量的一阶微分方程，故首先将关于时间的二阶微分方程改写成等价的一阶微分方程组：

(6)

(7)

记Y(t)=(u1,u2,…,uM-1,v1,v2,…,vM-1)T,则上式可以写成矩阵形式：

Y′(t)=HY(t)

(8)

利用初始条件Y(tn)=Yn，在区间[tn,tn+1]上对(8)式进行积分，得

Yn+1=T(Yn+Q)-Q

(9)

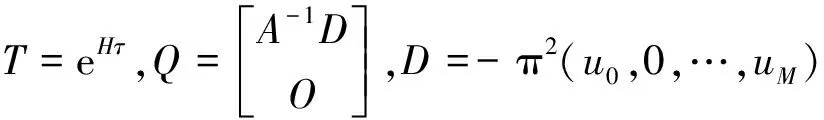
利用公式(9)进行递推计算时，需先算出列向量Q和指数矩阵T.

1.3 精细时程积分法

首先给出指数矩阵T(τ)=exp(Hτ)，其中τ=tk+1-tk,H为矩阵的计算方法.

将T(τ)表示为

(10)

(11)

因此矩阵T(τ)可表示为

T(τ)=[exp(HΔt)]2N=(I+Tα)2N-1(I+Tα)2N-1

(12)

其中I是单位矩阵，这样的分解一直做N次，便可以得到T(τ)的高精确度值.

因为H是常矩阵，式(11)的通解可以写成Y(t)=exp(Ht)Y0.

Yn+1=TYn

(13)

(14)

表1 数值算例结果

迭代N次，然后取T=I+TN即可.只要正整数N,J适当大，就能保证T有足够的精确度.

2 数值算例

取l=1，a2=π2，g1(x)=sin(πx)+1，g2(x)=0，g3(t)=1，N=20,J=5.用拟小波-精细时程积分法进行计算,结果如表1所示.由于问题的对称性，表中只列出了左半根梁的计算结果，该问题的精确解为u=1+sinπxcosπt(计算总时间均为10 s).

利用文[4]的有限差分法计算τ=0.1,h=0.05, 得到数据的相对误差为10-4数量级，可见本文的拟Shannon小波精细积分法有10-6数量级的相对误差.

3 结 论

(1)空间步长越小，计算的精度越高.

(2)在使用迭代公式计算指数矩阵T时，正整数N和J的值越大计算结果越精确，算例表示取N=20,J=5就能得到较好的精确度.

(3)精细时程积分法中的时间步长可以取较大的值，并且可以长时间计算.

参考文献

[1] 倪 平，高仪新. 梁振动力方程的广义差分法[J]. 东北师范大学学报(自然科学版),1995,(4):14-19.

[2] 曾文平. 四阶杆振动方程的含参数四层显式差分格式[J]. 华侨大学学报(自然科学版)，2002，23(2):116-121.

[3] 曾文平. 解四阶杆振动方程新的两类隐式差分格式[J]. 华侨大学学报(自然科学版)，2003，24(2):136-142.

[4] 金承日，王玉兰，刘明珠. 解四阶杆振动方程的精细时程积分法[J]. 哈尔滨工业大学学报，2005，37(8):1 043-1 045.

[5] 赵丽滨，张建宇，王寿梅. 精细时程积分方法的稳定性和精度分析[J].北京航空航天大学学报，2000,26(5):569-572.