基于LS-SVR算法改进的RBF神经网络及其在股价预测中的应用
2011-02-20贺瑞缠
程 曦, 贺瑞缠
(西北大学数学系, 陕西 西安 710127)
0 引 言
径向基函数神经网络(Radial Basis Function Neural Network, RBFNN)是20世纪80年代末由莫迪(J.Moody)和达肯(C.Darken)提出的[1],其具有结构简单、逼近能力强和收敛速度快等优点,现已证明它能以任意精度逼近任意连续函数[2].但是对于径向基函数中心和径向基函数宽度的确定,以及如何解决 “维数灾难”等问题,仍然是RBF神经网络的研究重点.支持向量机(Support Vector Machines, SVM)是Vapnik等人基于统计学习理论中的结构风险最小化原则提出的[3].最小二乘支持向量机(Least Squares Support Vector Machines, LS-SVM)是一种新兴的支持向量机方法,由于其算法中只有参数是待选的,比支持向量机的其他算法待选参数少,所以具有良好的稳定性,并且其运算速度较快,但其稀疏性相对较差.RBF神经网络在预测无噪声数据时精度较高,而对于有噪声数据,其预测精度则明显下降,这说明其稳定性较差.本文利用LS-SVR算法求解出的支持向量的个数确定RBF网络的隐层节点数目,支持向量作为网络中心,从而构造出RBF神经网络较优的初始结构和网络参数,再用梯度下降法微调网络参数,使网络性能达到最优,并将该算法应用于个股股价的短期预测中,取得了良好的预测效果.
1 RBF神经网络与支持向量机的结构
RBF神经网络是一种局部逼近网络,并且具有最佳逼近特性.其网络结构是一种三层前馈型网络.输入层的作用是将输入向量直接传输至隐层节点,用隐层包含的一系列径向基函数来逼近未知函数,所以RBF的网络结构为:
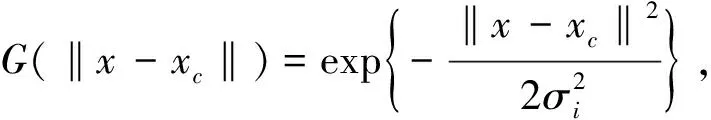
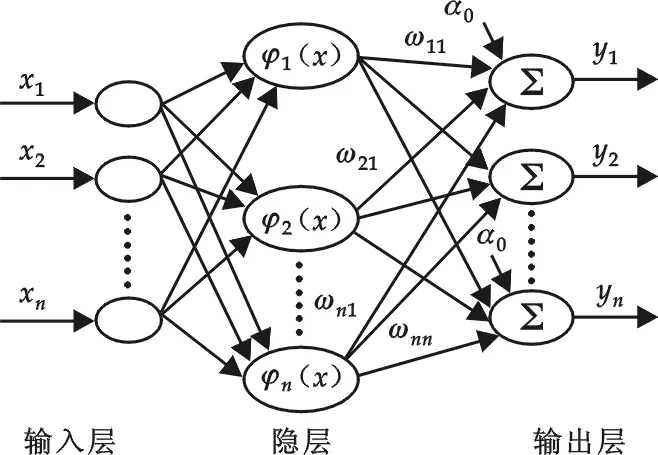
图1 RBF神经网络结构示意
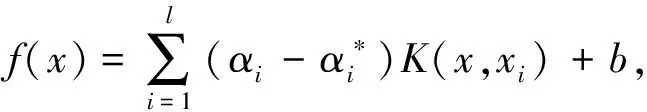
综上可知,RBF神经网络与支持向量机虽然在算法上存在着本质区别,但是其二者的结构有相似之处.现已证明,选取满足条件的支持向量核函数,用支持向量回归方法所确定的两层网络结构模型在本质上进一步等价于加权平均输出的径向基函数网络[5],因此本文将支持向量回归算法应用到RBF神经网络的训练中,以提高RBF网络的性能.
2 基于LS-SVR算法改进的RBF神经网络
f(x)=ωφ(x)+b
而LS-SVR的原始优化问题为:
构造其拉格朗日函数为:
现对各个参数求偏导并令其为零,可得:
将上式写成矩阵形式有:
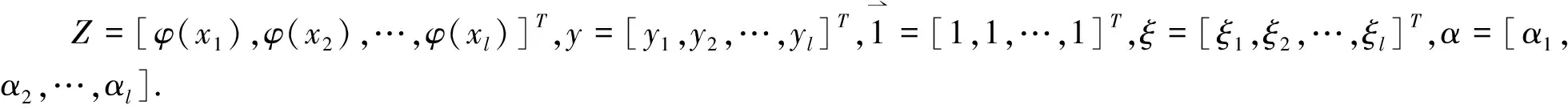
根据核函数的相关思想以及Mercer定理,我们用核函数K(xi,xj)代替高位空间中的内积运算,并消去ω和ξ,上式可变为:
求解上式得出非线性回归函数:
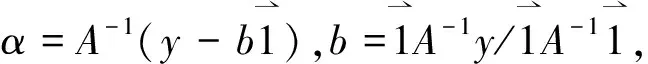
由LS-SVR算法构造网络的初始结构,选用高斯径向基核函数作为网络的隐层,则新的网络结构可表示为:
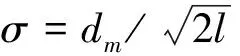
3 网络的学习算法
在RBF网络的学习过程中,调整径向基函数的中心、宽度以及网络权值等网络参数,使网络性能达到最优.本文选择梯度下降法作为其训练算法.
对于RBF的网络结构:
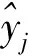
求J对ωij、ci、σi的偏导数,得:
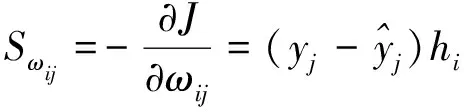
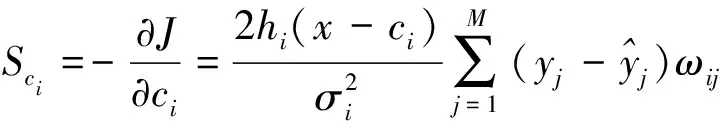
因此,各参数的校正公式如下:
ωij(n+1)=ωij(n)+λSωij
ci(n+1)=ci(n)+λScj
σi(n+1)=σi(n)+λSσi
其中1≤i≤l,1≤j≤M;l是隐节点数目,M是输出维数,λ是步长,通常取0.05.
4 实例分析
股票价格是一种非线性离散时间序列,由股票的价值所决定, 但同时也受到其他因素的影响. 其中, 供求关系是最直接的因素, 其他因素都是通过作用于供求关系而影响股票价格的[6].本文选取深圳交易所A股青岛双星(000599)2009年06月02日至2011年06月02日共计486个交易日记录作为训练数据,并将2011年06月03日至2011年08月12日共计50个交易日记录作为测试数据,分别将其每日开盘价、每日最高价、每日最低价、每日收盘价、每日成交量、每日成交额6个变量作为网络输入变量,未来50日的开盘价作为输出变量,由此来预测股票的短期价格走势,其预测结果如图2所示.
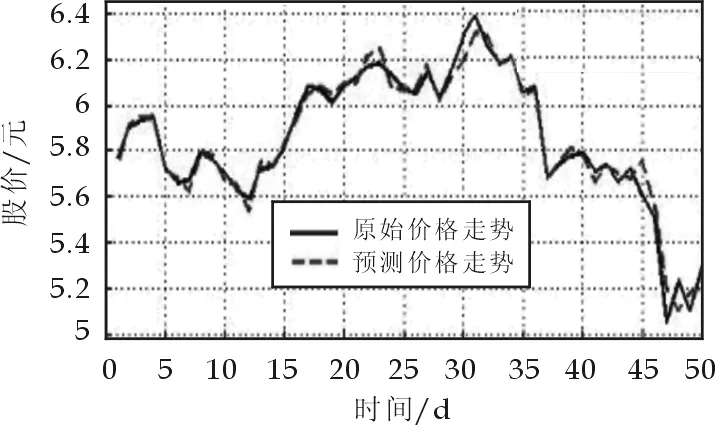
图2 股票价格回归预测曲线(50天)

表1 误差率的统计分析表
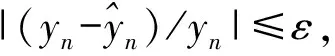
5 结束语
作者基于LS-SVR算法改进的RBF神经网络通过LSSVR算法得到了RBF网络较优的初始结构和参数,并通过梯度下降法微调网络参数,使网络性能达到最优,将改进后的网络用于股票价格预测实例,取得了良好的学习性能和预测效果.
参考文献
[1] Moody J,Darken CJ.Fast learning in networks of locally tuned processing units[J].Neural Computation,1989(1):281-294.
[2] 程建国.神经计算与生长自组织网络[M].西安:西安交通大学出版社,2008:66-69.
[3] Vapnik V N.Statistical Learning Theory[M].New York:Wiley,1998.
[4] 吴今培,孙德山.现代数据分析[M].北京:机械工业出版社,2006:92-96.
[5] 李 军,赵 锋.基于支持向量回归神经网络的时间序列预测[J].系统仿真学报,2008,20(15):4 025-4 030.
[6] 殷洪才,赵春燕.基于神经网络股票预测的研究[J].哈尔滨师范大学自然科学学报,2007,23(3):47-49.
