基于性能退化数据的加工中心的可靠性评估

杨志伟， 任工昌， 孟勃敏

(陕西科技大学机电工程学院， 陕西 西安 710021)

0 引 言

由于大部分产品的失效机理最终可以追溯到产品潜在的性能退化过程，因此从某种意义上可以认为性能退化最终导致了产品失效(或故障)的产生.因此产品实际的失效时间可以通过估计产品在给定应力下的退化轨迹外推确定，可以使用性能退化数据分析代替传统的失效数据分析来进行产品的可靠性评估[1].本文以某机床厂生产的加工心中为研究对象，通过对加工中心进行机械应力仿真试验后，利用试验后所测得的数据建立了基于性能退化的灰色理论模型，采用极小子样本的威伯斯先验法对加工中心进行了可靠性评估.

1 加工中心的机械应力仿真实验

为了判断产品的退化失效情况，通常选几项主要技术性能指标作为性能退化特性参数，当这几项技术性能指标中一项或几项超出设计任务书规定的范围，则产品出现退化失效[2].由于数控机床性能退化情况最终反映在数控机床输出终端可执行部件的位移、速度和加速度等异常变化，数控机床定位精度、重复定位精度是影响数控机床加工精度的主要因素，也是评价数控机床的重要检测内容.本文采用定位精度和重复定位精度作为性能退化特征参数.

机械故障的失效模式主要表现为疲劳、断裂、磨损、老化、松动等，失效可以通过施加载荷反映出来.为此，本文对加工中心的性能退化可靠性试验，采取对主轴系统和进给系统进行仿真切削力加载试验.在可靠性退化试验过程中，为了模拟加工中心的实际切削工作状况，在每次测量数据之间的14小时内对加工中心进行机械应力仿真加载，然后用激光测试仪测量加工中心定位精度和重复定位精度.对所测量的数据进行统计整理后，获得加工中心的X轴、Y轴和Z轴的定位精度和重复定位精度9组数据，如表1所示，表中数据单位为：mm.

表1 定位精度、重复定位精度数据表

2 性能退化数学模型的建立

灰色系统理论以部分信息已知，部分信息未知的小样本、贫信息不确定性系统为研究对象，主要通过对部分已知信息的生成、开发，提取有价值的信息，实现对系统行为、演化规律的正确认识和有效控制[3].灰色系统模型对试验数据及其分布没有特殊的要求和限制.

2.1 GM(1，1)模型简介[4,5]

设X(0)为非负序列，X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，其中，x(0)(k)≥0，k=1,2,…,n.

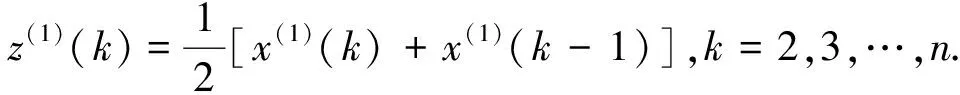
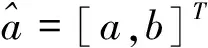
(2)GM(1,1)模型

(3)还原值

对于失效阈值的序列数为k+1，时距间隔为14 h，伪失效寿命为(k+1)×14 h.

2.2 性能退化数学模型的建立

本文以X轴的定位精度和重复定位精度为例按照灰色理论的方法，建立退化性能数学模型，并取定位精度、重复定位精度前8个数据.

X={x(1)，x(2)，x(3)，x(4)，x(5)，x(6)，x(7)，x(8)}={0.003 002，0.003 035，0.003 071，0.003 106，0.003 139，0.003 189，0.003 212，0.003 266}

XX={xx(1)，xx(2)，xx(3)，xx(4)，xx(5)，xx(6)，xx(7)，xx(8)}= {0.002 608，0.002 619，0.002 632，0.002 649，0.002 661，0.002 673，0.002 690，0.002 709}

其时间响应序列分别为

序列还原值分别为

失效阈值为0.008，伪失效寿命为1 157.58 h.

失效阈值为0.004，伪失效寿命为1 106.27 h.

3 基于威伯斯先验法的可靠性评估

由于加工中心这类产品大型复杂，成本极其昂贵，批量较小，因此对于这类产品进行较大的样本量(样本量n≥10)的试验，在财力上是难以接受的.对于加工中心这样的高可靠性产品，可靠性试验往往只能是n=1或n=2的极小样本[7].

威伯斯先验评估法是在统计学的贝叶斯方法的基础上推演与发展而来的，也是威布尔分布分析技术的分支和推广[8].威伯斯先验评估法是利用同类产品中，已获得的试验数据值对其进行威布尔分析，获得形状参数β值，即为先验数据的β值.再利用无数据支持的计算方法得到尺度参数(特征寿命)，然后进行计算便可得到可靠性参数和平均寿命值等[9].在本次试验中，只得到单个样本寿命数据，形状参数β取值为该系列加工中心的先验形状参数β=1.213，试验所得寿命值即是特征寿命值α.

将最小的伪失效寿命作为整机伪失效寿命，且将该单样本数据作为两参数威布尔分布的特征寿命，将前期收集的故障数据两参数威布尔分布形状参数作为先验数据的形状参数值，可得寿命分布模型.

两参数威布尔分布概率密度函数

4 结束语

本文以加工中心轴线的定位精度和重复定位精度的性能退化数据作为该加工中心的性能退化特征量，利用灰色理论建立了性能退化数学模型，推算出了伪失效寿命.利用威伯斯先验法，以最小伪失效寿命为模型特征寿命，评估得到加工中心平均寿命为1 037.77 h；同时也可以考虑以加工中心实际加工过程中的特征量作为性能退化特征量.

参考文献

[1] 邓爱民，陈 循，张春华,等．基于性能退化数据的可靠性评估[J]．宇航学报，2006,27(3)，546-552.

[2] 贾占强，梁玉英，蔡金燕．基于加速性能退化试验的板级可靠性评估[J]．无线电工程，2008,38(2)，46-50.

[3] 贾占强，梁玉英，蔡金燕．基于灰色系统理论的产生与发展[J]．南京航空航天大学学报，2004,36(2)，267-261.

[4] 陈永光，柯宏发．电子信息装备试验灰色系统理论运用技术[M]．北京：国防工业出版社，2008．

[5] 罗佑新．灰色系统理论及其在机械工程中的应用[M]．长沙：国防科技大学出版社 , 2001．

[6] 刘思峰，谢乃明．灰色系统理论及其应用[M]．北京：科学出版社，2008．

[7] 冯蕴雯，黄 玮，吕震宇,等.极小子样试验的半经验评估方法[J].航空学报，2004,25(5)，456-459.

[8] 宋兆泓，付小平，吴树雄．某涡轮盘小子样低周疲劳寿命评估计算——威伯斯先验评估法[J]．航空发动机，2002(3)：18-20．

[9] 赵 宇，杨 军，马小兵．可靠性数据分析教程[M]．北京：北京航空航天大学出版社，2009．