一类具有脉冲效应的捕食系统分析
2011-02-20卢琨
卢 琨
(陕西科技大学理学院, 陕西 西安 710021)
0 引 言
捕食者-食饵系统是非常重要的数学模型,近几年来,脉冲微分方程被引入种群动力学中,并且得到了广泛的应用[1-6].本文研究了下面具有非单调功能反应且对捕食者进行周期投放的捕食者-食饵系统
(1)
这里x(t),y(t)分别代表食饵(害虫)种群和捕食者(天敌)种群的密度,r是食饵的内禀增长率,β是食饵的种内竞争系数,ω代表捕食者的转化率,d代表捕食者的死亡率.这里所有的参数都是正数,函数f(x)=sx(t)exp(-kx(t))是功能反应函数,具有非单调性.
T是脉冲周期n∈N,本文考虑通过在整周期释放天敌对模型进行分析,q≥0是每次释放的天敌数量.
1 预备知识
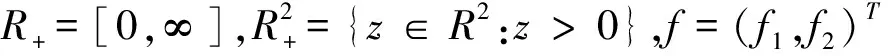
定义1 系统(1)是持续生存的,如果存在正常数m,M和T0,使得系统(1)的所有正解(x(t),y(t))都满足当t>T0时有m≤x(t)≤M,m≤y(t)≤M.
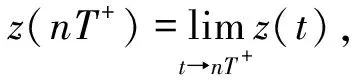
引理1 设z(t)是系统(1)的解,并且满足初值条件z(0+)≥0,于是对所有t≥0,都有z(t)≥0,且如果z(0+)>0,则t≥0时z(t)>0.
当食饵灭绝时,捕食者满足方程:
(2)
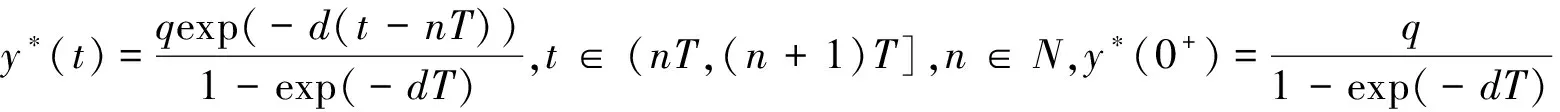
引理2 系统(2)有一个正周期解y*(t),并且对系统(2)的满足y0≥0的任意解y(t)有|y(t)-y*(t)|→0,t→∞.
把上面的结论应用到系统(1)中,即可得到系统(1)的食饵(害虫)灭绝的周期解:
2 灭绝与持续生存
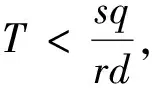
证明 设(x(t),y(t))是系统(1)的任意解,做变换x(t)=u(t),y(t)=v(t)+y*(t),则相应的线性方程组的解为
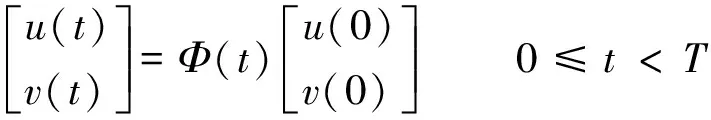
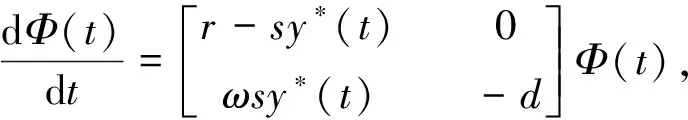
系统(1)的脉冲条件变为
定理2 一定存在常数M,使得系统(1)的解x(t),y(t),满足当t充分大时,有x(t)≤M,y(t)≤M.
证明 设x(t),y(t)是系统(1)的任意解,令V(t)=ωx(t)+y(t),显然V∈V0,且
(3)
显然,当0<λ D+V(t)+λ0V(t)≤L1(L1有界),这样方程(3)即为 由文献[2]中的引理2.2知,当t∈(nT,(n+1)T)时 于是有 因此,由V(t)的定义知存在一个常数M>0,使得t充分大时系统(1)的每个解都有x(t)≤M,y(t)≤M,即系统(1)的解是一致最终有界的,证毕. 由脉冲微分方程比较定理[3]和引理1易得t充分大时,y(t)>m2.我们只需找到m1>0,使当t充分大时有x(t)≥m1,下面分两步来证明: 其中-d+ωsm3<0. (4) (5) 令N1∈N和N1T≥T1,将上面方程组的第一个方程在(nT,(n+1)T] (n≥N1)上积分得 因此,当k→∞时有x((N1+k)T)≥x(N1T)σk→∞,这与x的有界性矛盾,因此存在t1>0,使得x(t1)≥m3. 如果t*是脉冲点,一定存在n0∈N使得t*=n0T,对于足够小的ε*>0,令t*=t*-ε*,有t*是非脉冲点,使得x(t*)≥m3. 现在设t*是非脉冲点,则当t∈[t1,t*]时,x(t)≥m3,并且因为x(t)是连续函数,有x(t*)=m3.设t*∈(nT,(n+1)T],选取n2,n3∈N,使得 σn3exp(n2αT)>σn3exp((n2+1)αT)>1 如前一步证明,我们有x((n1+1+n2+n3)T)≥x((n1+1+n2)T)σn3,由系统(1)的第一个方程得 (6) 在t∈[t*,(n1+1+n2)T]上对上式积分得 x((n1+1+n2)T)≥m3exp(α(n2+1)T) (7) 因此x((n1+1+n2+n3)T)≥m3σn3exp((n2+1)T)≥m3,矛盾. x(t)≥x(t*)exp(α(t-t*))≥m3exp((1+n2+n3)αT)=m1 因此x(t1)≥m1,对所有的t≥t1都成立,证毕. 本文利用脉冲微分方程Floquet乘子理论和比较定理,得到了对捕食者进行周期投放的捕食者-食饵系统持续生存的条件,其结果可以应用到诸如农业生产的很多方面中.在捕食者-食饵系统的讨论中,综合害虫管理(IPM)同样是农业生产中控制害虫的一种非常有效的方法,在以后的研究中,作者会尝试对捕食者进行周期投放和对食饵进行周期喷洒农药同时作用于系统,期望同样可以得到系统持续生存的条件. 参考文献 [1] 王晓琴.一类具有Watt型功能性反应生态系统的脉冲控制研究[D].西安:陕西科技大学硕士学位论文,2006. [2] Bainov DD,Simeonov PS.Impulsive Differential Equations:Asymptotic Properties of the Solutions[M].Singapore: World Scientific,1993:1-120. [3] Lakshm Ikantham V,Banov D D,Smeonov P S.Theory of Impulsive Differential Equations[M].Singapore:World Scientific,1989. [4] 贾建文,乔梅红.一类具有脉冲效应和Ⅲ类功能反映的捕食系统分析[J].生物数学学报,2008,23(2):279-288. [5] 何德才.对脉冲扰动下一类具类功能反应种群模型的分析[J].内蒙古师范大学学报,2008,(37):733-736. [6] Ruiqing Shi,Xiaowu Jiang,Lansun Chen.A predator-prey model with disease in the prey and two impulses for integrated pest management[J].Applied Mathematical Modelling,2009,(33):2 248-2 256.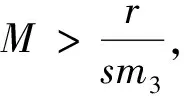
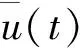
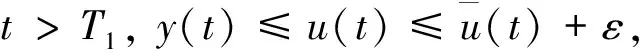
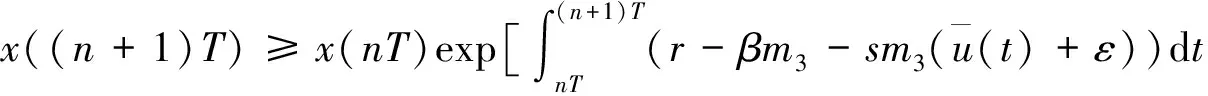
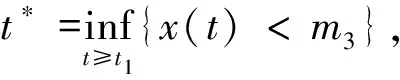
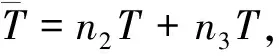
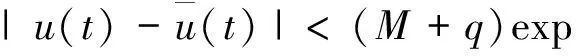
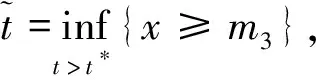
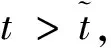
4 结束语
