上证指数的基于小波的NN-GARCH模型及实证研究

王若星， 张德生， 彭潇熟

(西安理工大学理学院， 陕西 西安 710054)

0 引 言

从以往众多的对中国证券市场的实证分析中我们可以知道：证券市场的波动性不仅随时间变化，而且过去回报的干扰项不对称地影响着未来的波动性.投机性价格的变化和收益率的变化具有稳定时期和易变时期，即价格波动呈现集群性，方差随时间变化.基于以上特点的模型有很多，其中广义自回归条件异方差(GARCH)模型族是比较常用的选择.如谈琳琳[1]基于GARCH模型对沪深两市的波动性进行了分析；刘妹伶等[2]基于GARCH模型对人民币/美元汇率进行了预测.

由于人工神经网络能够较好地体现过去的干扰项与未来波动性的非线性关系，所以人工神经网络对证券市场的分析也比较成功，并且神经网络在预测满足以下条件的问题时特别有效: (1)自变量和因变量之间的关系没有已知的数学方程；(2)预测比解释更重要；(3)有足够多的数据可供建模.这正好是金融时间序列所需要的.NN-GARCH模型就是将神经网络应用于金融时间序列建模的方法，它是一个在均值方程中具有非线性神经网络参数，方差方程中具有线性GARCH参数的模型，同时优点还体现在每一步建模过程都被清楚的论证并且实施，包括输入变量的选择，神经网络隐含单元的个数都是通过严格的检验得到的.因此，相对于传统的神经网络研究方法，NN-GARCH模型更加科学，更具有实用性.

另外，在以往的建模过程中，往往不考虑数据中的噪声影响而直接对原始数据建立模型，实际上，噪声会影响分析、预测的准确度，相比其它的滤波方法，小波变换具有良好的时域和频域分析能力，它将时间序列作为信号序列分解为具有不同振幅、相位和频率的周期分量的叠加，可以寻找序列中隐含的内在因素，因而在处理非平稳信号上有其特殊的效果.邓凯旭等[3]将小波多分辨分析理论与自回归(AR)模型结合起来进行线性预测，得到了优于传统AR模型的预测效果.

本文首先将神经网络与GARCH模型结合，得到含单隐含层的前馈神经网络时间序列模型(NN-GARCH)，然后将小波多分辨分析与NN-GARCH模型结合，建立了基于小波的NN-GARCH模型，最后对上证指数进行了实证分析.

1 小波多分辨分析[4]

小波多分辨分析可以通过Mallat算法实现.Mallat分解算法如下：

(1)

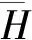
当分解进行到J-1层时，原始信号被分解为J-1个高频信号和一个低频信号.对这些信号再进行重构结果如下

Vj=HVj+1+GWj+1

(2)

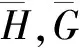
2 NN-GARCH模型

2.1 ARCH模型

ARCH模型[5]的主要思想为扰动项εt的条件方差依赖于它的前期值的大小，通过对序列的均值和方差同时建模.设yt为因变量，xt为解释变量，在t时刻可获得的信息集为Ωt-1的条件下，误差项εt以0为期望值，ht为条件方差的正态分布.以ARCH(q)为例，均值方程为：

yt=Xtβ+εt

(3)

随机干扰项的平方ε2服从AR(p)过程，可用下面方程表示：

(4)

(5)

其中，vt独立分布，E(vt)=0,D(vt)=1;a0>0,ai≥0(i=1,2,…,q),且a0+a1+…+aq<1，则称误差项εt服从q阶的ARCH过程，计作εt～ARCH(q)过程.ARCH(q)模型表明过去的波动对市场未来的不断有着正向而缓解的影响，因此波动会持续，从而模拟了市场波动的集群性现象.

2.2 GARCH模型

在实际应用中，ARCH模型往往难以估计参数数量众多的模型.为克服这一困难，Bollerslev(1986)[6]提出了广义ARCH模型，即GARCH模型或GARCH(p,q)模型.与ARCH模型一样，GARCH模型通常也用于对回归或自回归模型的随机扰动项进行建模.GARCH模型的条件方差表达如下:

(6)

为保证条件方差ht>0，要求a0>0,ai≥0,i=1,2,…,q,βj≥0,j=1,2,…,p.

用GARCH(p,q)表示阶数为p和q的GARCH过程.为了保证GARCH(p,q)是宽平稳的，存在参数约束条件α+β<1.

2.3 NN-GARCH模型

Nikos S.Thomaidis等(2005)[7]定义均值方程为线性自回归和神经网络参数的混合模型，它的一般形式为：

(7)

εt|Zt～N(0,ht)

(8)

(9)

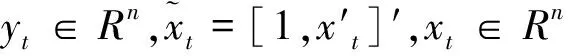
(10)

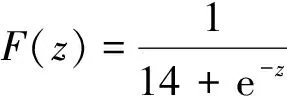
3 基于小波分析的NN-GARCH模型

我们的目标是得到既能较准确的对股票数据进行拟合和预测，又能得到最简洁的模型.以下是我们建模的具体过程：

(1) 对原始信号选用适当的小波函数，使用式(1)进行小波分解，根据小波多分辩分析的理论[4]，分解的层次越高，去掉的低频成份就越多，丢失的有用信息也越多.为了建立合理的模型，一般分解不应超过3层.然后利用式(2)对分解后的各层信号进行单支重构，即得单支重构后的信号W1,W2,…,WJ-1和VJ-1；

(2) 对WJ(1≤J≤J-1)和VJ-1分别建立NN-GARCH模型，并估计其参数；

(3) 对建立的模型的合理性进行检验；

从而得到原时间序列的预测值为

(11)

NN-GARCH模型的建模过程为：

(1)由一个线性模型开始，在同方差假定下，依据最小二乘准则(LS criterion)估计一个无GARCH效应的线性AR(p)方程：

(12)

(2)设定一个显著性水平(如a%)，检验原假设真实数据的生成过程是一个线性过程；备择假设：

数据的生成过程是含有单隐含层的神经网络模型(Ⅰ).如果在给定的显著性水平下线性性不被拒绝，则停止.否则，用NLS方法估计含有单一神经元的神经网络模型，并在αρ,0<ρ<1的显著性水平下，检验备择假设：再加入一个额外神经元(即含有两个神经元)的神经网络模型(Ⅱ).如果零假设不被拒绝，则停止.否则，对于含有h个神经元的神经网络模型(h=2,3,…)重复上面的过程，直到首次接受零假设为止.在每一次接下来的检验中都将显著性水平降低，直到收敛至0为止，在本文中，我们取ρ=1/2，这样就可以避免过度拟合数据，也避免估计出过于冗余的模型，从而控制住整个过程的显著性水平.

(3)估计出了合适的条件均值方程，利用Engle(1982)[5]提出的LM检验，在给定的阶数下检验方程有无ARCH效应，即检验原假设:模型的残差序列中不存在ARCH效应，备择假设：残差序列在给定的阶数下存在ARCH效应.如果原假设不被拒绝，则停止.否则：

(a) 开始用条件均值方程的残差序列估计一个GARCH(l,1)模型.

(b) 联合估计NN-GARCH(1,1)模型的参数.

(c) 删掉不显著的参数并重新估计模型.

4 实证研究

4.1 原始数据

本文对上证指数进行了实证研究.取样时间是从2008年4月23日至2010年6月10日，不包括没有交易的日子，共523个数据，原始数据来源于大智慧软件.原始数据见图1.

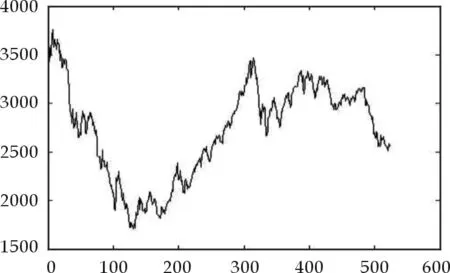
图1 原始数据

首先进行小波分解，将数据分解得到一个逼近序列和2个细节序列，然后采用ADF方法进行平稳性检验，结果表明：逼近序列不平稳，而两个细节序列是平稳的.对逼近序列采用对数差分进行平稳化处理:Yt=100(lnXt-lnXt-1).用前508个数据建立模型，用剩下的15个数据评价模型.本文用 Eviews 6.0处理时间序列，用Matlab处理神经网络及其诊断检验.

4.2 小波分解与重构

经过多次实验，本文利用Daubechies小波系中的db2对原信号进行2尺度分解，得到一个逼近序列和2个细节序列(图2).

对分解后的不同子序列采用ADF检验法进行平稳性检验，然后对非平稳的序列进行平稳化处理.从图3得出重构近似系数CA2，经ADF检验为非平稳序列，对其取对数再一阶差分进行平稳化处理，通过ADF检验平稳(表1)，得到序列{xt}，最后利用第三部分介绍的方法分别建立NN-GARCH模型，利用AIC准则和SBIC准则选择结点的个数和滞后变量.并对单支重构后的时间序列(图3)分别进行预测，最后，把预测值相加得到原始序列的预测值.

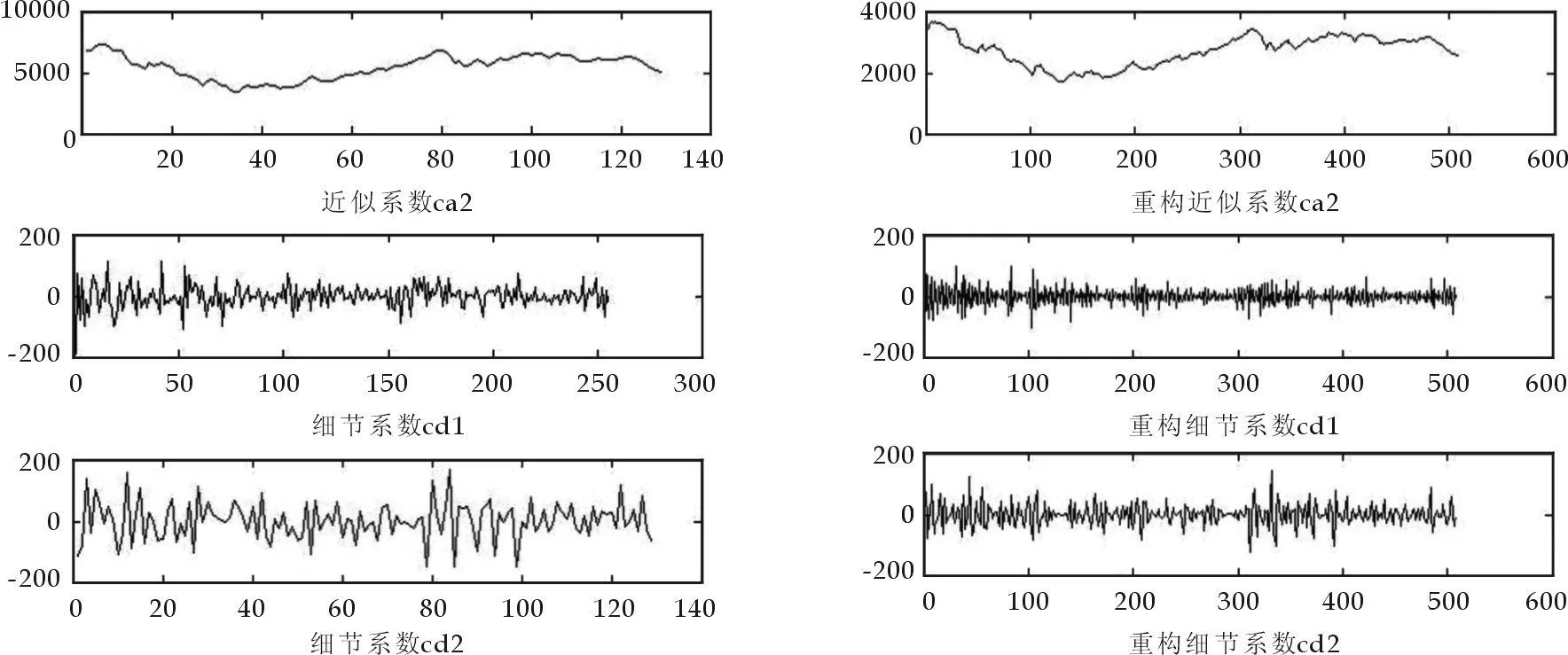
图2 小波分解 图3 小波重构

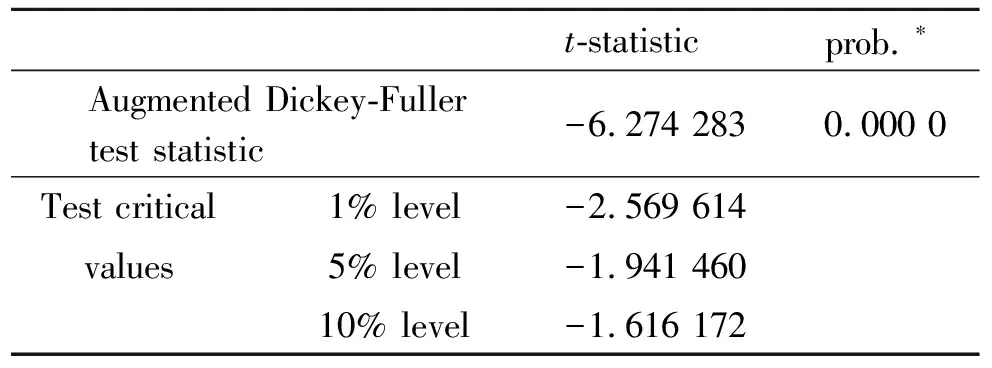
表1 近似细节数对数差分后的ADF检验结果

4.3 建立基于小波的NN-GARCH模型

利用3中方法对经过平稳化处理后的重构近似系数{xt}进行建模，用2008年4月23日～2010年5月20日共508个数值建立模型和预报方程，其中变量的选择采用AIC、BIC及SBIC准则进行选取.并对2010年5月21日～6月3日共10个数值进行预报.用Matlab编程，并经过还原处理，得到近似系数序列的拟合结果和预测结果.

再分别对重构细节系数CD1序列和CD2序列按照3中的步骤建立NN-GARCH模型，将它们的拟合、预测结果和重构近似细节CA2的拟合、预测结果相加，作为最终的拟合、预测结果.最后，将此模型的预测结果与未加小波的NN-GARCH模型以及AR-NN模型的预测结果进行比较，结果见表2.

CA2序列建模结果：

yt= -99.21-3.99yt-1-6.05yt-4-7.86yt-8+191.90F[0.23(0.42yt-1+0.52yt-4+0.74yt-8

ht=0.73-0.03εt2+0.26ht-1

(13)

CD1序列建模结果：

yt= 2.49-0.99yt-1-1.39yt-2-0.96yt-3-0.21yt-4

+41.47F[0.19(0.59yt-1+0.76yt-2+0.29yt-4-0.15)]

ht=109.39+0.45εt2-0.07ht-1

(14)

CD2序列建模结果：

yt= 18.29+1.24yt-1-2.10yt-2+0.92yt-3-1.05yt-4

-185.94F[0.12(1.07yt-1+1.40yt-2+0.63yt-4+0.88)]

ht=13.63+0.10εt2+0.82ht-1

(15)

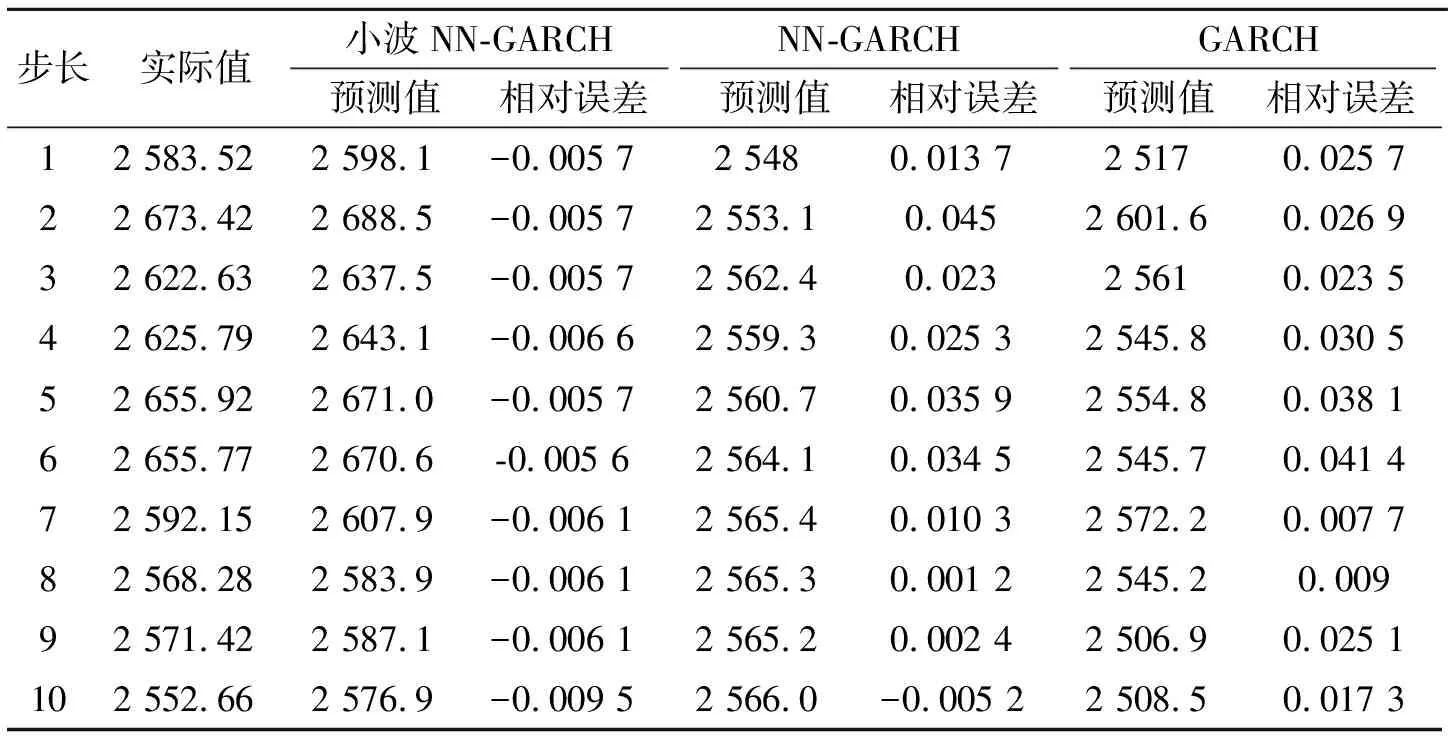
表2 各模型预测结果对比

注相对误差=(实际值-预测值)/实际值.

利用平均绝对误差MAE与均方误差MSE比较预测效果，结果见表3，计算公式为：

(16)

从表2可以看出：基于小波的NN-GARCH模型的预测结果的相对误差比NN-GARCH和GARCH两个模型的预测结果的相对误差小.从表3也可以看出：基于小波的NN-GARCH模型的预测结果的MAE和MSE比其它两个模型的预测结果的MAE和MSE小.

表3 各模型预测结果MAE、MSE对比

5 结 论

本文对上证指数建立了基于小波的NN-GARCH模型，并与加入神经元的NN-GARCH模型以及单纯的GARCH模型的预测结果进行了比较，从实证研究结果可以看出：加入神经元(NN)的小波GARCH模型的预测效果比只含有神经元的GARCH模型的预测效果好，同时只含有神经元的GARCH模型的预测效果优于单纯的GARCH模型的预测效果.这主要是因为不仅GARCH模型可以消除异方差性，小波多分辨分析还可以去除偶然因素造成的噪声影响，提高预测的精度，而加入神经元又可以更好的利用神经网络的特性来拟合数据的非线性性.所以，基于小波的NN-GARCH模型可以对时间序列作出更准确的预测.

参考文献

[1] 谈琳琳. 基于GARCH模型的沪深两市波动性分析[J]. 当代经济，2008，(8): 154-156.

[2] 刘妹伶，温 涛，葛 军.人民币汇率预测及方法选择——基于ARIMA与GARCH模型[J]. 技术经济与管理研究，2008，159(4)：91-93.

[3] 邓凯旭，宋宝瑞. 小波变换在金融数据分析中的应用[J]. 数理统计与管理，2006，25(2):215-219.

[4] 程正兴. 小波分析算法与应用[M]. 西安：西安交通大学出版社，1998.

[5] Engel. Auto regressive conditional hetero skedasticity with estimates of U.K inflation[J]. Econometrics,1982,(50)：987-1008.

[6] Bollerslew Tim. Generalized auto regressive conditional hetero scedasticity[J].Journal of Econometric-s, 1986,(2):31-32.

[7] N.S. Thomaidis, G.Dounias, N. Kondakis. Financial statistical modeling with a new nature-inspired technique[C]. Proc. of the 1st European Symposium on Nature-Inspired Smart-Information Systems(NISIS), Albufeira, Portugal, 2005.