一种用于大功率电弧加热器的 等离子电弧模型

戴隽文 郝瑞祥 游小杰

（北京交通大学电气工程学院 北京 100044）

1 引言

电弧加热器是一种能产生高温的热源设备，近年来在航空、航天、材料加工等领域中起着日益重要的作用。等离子电弧是一种非线性负载，为研制安全可靠、控制品质优越的大功率直流电弧加热器电源系统，等离子电弧模型的建立显得尤为重要。

目前国内外研究较多的电弧模型主要有基于热力学、等离子体物理学、电磁场理论等各门学科的磁流体（MHD）模型[1]，基于等离子体控制方程的电弧模型[2]，基于数值拟合的电弧模型[3]，基于经验公式的电弧模型[4]，以及基于麦也尔（Mayr）模型和克西（Cassie）模型的电弧黑盒模型[5]。MHD模型推导严密，物理概念清晰，但其边界条件的推导需要大量实验数据支持，否则难以实现。基于等离子体控制方程的电弧模型能较好地描述电弧特性，但其求解方法复杂，结果有发散或振荡的可能。基于数值拟合的电弧模型能准确描述某特定场合的电弧特性，但其不具备通用性。基于经验公式的电弧模型表达式简单，但精度不高，且参数确定较为困难。

本文讨论的电弧模型是基于黑盒模型Mayr 模型和Cassie 模型提出的。Mayr 模型和Cassie 模型物理意义明确，表达式简练，能较好地描述电弧特性，对电弧的定性分析有着重大意义[6]。常见的电弧黑盒模型大多应用在小功率交流场合，而本文对黑盒模型在大功率直流场合中的应用进行了探索。在实际工程中，电弧加热器工作时弧室中的气流量会发生一定变化，而这些变化不能直接在Mayr 模型和Cassie 模型中体现出来。为解决该问题，本文在文献[7]提出的模型基础上，增加了黑盒模型参数，并就每个参数对电弧特性的影响进行了分析。此外，本文还对Mayr 模型和Cassie 模型之间过渡函数的选取展开了讨论，使改进后的电弧模型能更真实地反映大功率直流电弧加热器的工作情况。在Matlab/Simulink 仿真环境下，用灵活的S 函数编写电弧的核心部分，令其作为负载，与恒流输出的18脉晶闸管全控整流桥组成一体，模拟实际大功率电弧加热器电源系统的工作情况。最后，通过与大功率直流电弧加热器实测工作数据的对比，验证了该等离子电弧模型的有效性。

2 电弧模型的建立

2.1 Mayr 模型和Cassie 模型

当把电弧作为电路的组成部分时，可以把它看成一个黑盒模型[6]。Mayr 模型和Cassie 模型是基于热平衡、热惯性、热游离三个基本平衡原理推导得出的两大经典的电弧黑盒模型，对于电弧的定性分析有着重大意义。

Mayr 认为电弧具有一个圆柱形气体通道的形状，其直径是恒定的。电弧散出能量是常数，即Ploss=P0=常数，因此Mayr 模型描述的电弧静特性曲线为双曲线形状，表达式为

Mayr 模型适用于小电流大电阻的情况，包括电流过零区的电弧工作情况，其模型微分表达式为

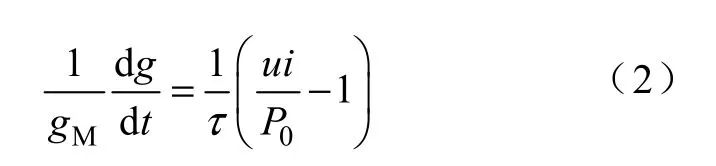
式中 u—瞬时电弧电压；

i—瞬时电弧电流；

P0—电弧散出功率；

gM—基于Mayr 模型的电弧电导。

Mayr 电弧模型的物理意义很明确，当电弧的输入功率ui 大于散出功率P0时，电弧温度将升高，热游离加强，电弧电导gM有增大的趋势。由于电弧有热惯性，因此有时间常数τ ，描述电弧电导变化速度。同样，当电弧产生的能量ui 小于散出功率P0时，电弧温度将降低，热游离减弱，电弧电导gM有减小的趋势。

Cassie 也认为电弧具有一个圆柱形气体通道的形状，但他认为其直径会随着电弧电流变化，以保持电弧电流密度恒定。Cassie 模型适用于大电流小电阻的情况，其模型微分表达式为

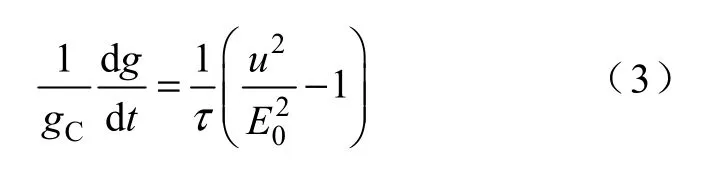
式中 u—瞬时电弧电压；

E0—电弧暂态稳定电压，E0的取值只受气流有关的弧柱形变过程影响，而与电流无关；

gC—基于Cassie 模型的电弧电导。

2.2 过渡函数的选取

电弧的伏安特性曲线是呈U 形变化的[8]，当电流较小时，符合Mayr 模型描述的情况；当电流较大时，符合Cassie 模型描述的情况。因此，要建立能完整描述电弧特性的模型，就要把两个模型综合起来。文献[9]提出了一种从电弧稳定性考虑的过渡函数，但由于函数值域问题，综合后的模型仅能描述大电流时电弧的工作情况，不能完整地描述小电流适用的Mayr 模型。

考虑到Mayr 模型和Cassie 模型分别描述了不同电流范围下的电弧特性，因此可建立以电流为变量的过渡函数σ (i)，令其以式（4）的形式，连接Mayr 模型和Cassie 模型。

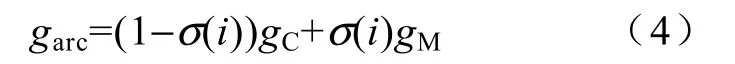
式中，过渡函数σ (i)∈（0，1]，是一个单调函数。通过对具有以上特性的函数进行多次仿真比较，选择过渡函数为

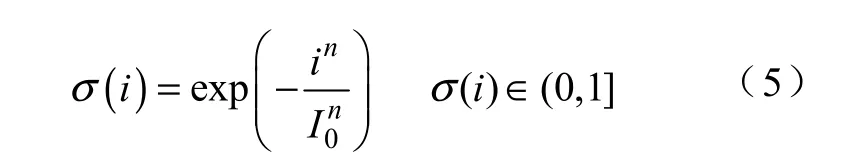
式中 i—电弧瞬时电流；

I0—过渡电流。

图1 是一组n 取不同值时，σ (i)变化的曲线簇。由图可知，n 越大，σ (i)变化速率越快，两个模型间过渡界限越明显。由于等离子电弧从负阻变化到正阻的过渡区，即U 形曲线的平直区较自由电弧明显减小[8]，因此n 取值稍大。经过多次比较，当n取1.2 时，仿真电弧静态曲线与实际电弧静态曲线拟合较好，此时，电弧模型表达式为

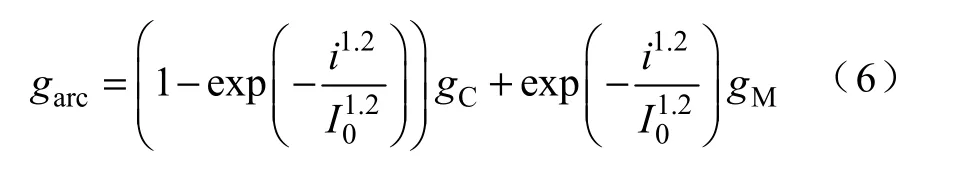
当电流较大时，σ (i)趋于0，电弧模型表现为Cassie 模型；当电弧电流较小时，σ (i)趋于1，电弧模型表现为Mayr 模型。因此，式（6）所示模型能够完整地描述电弧特性。

图1 n 对过渡函数的影响 Fig.1 Effect of n on the transition function

2.3 电弧模型的提出

本文所讨论的等离子电弧模型应用在如图2 所示的等离子电弧加热器中，涉及的变量主要有弧室气压p、气流量m、喉道尺寸d 等。当加热器工作时，p 和d 基本保持常量，但气流量m 会产生一定的变化。因此为了更真实地描述电弧加热器工作情况，要使模型能反映气流量m 的作用。

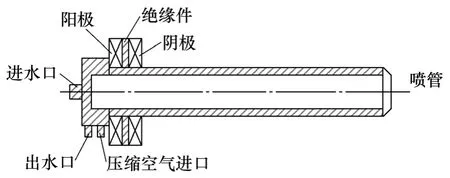
图2 等离子电弧加热器结构图 Fig.2 Configuration of arc heater

文献[10-11]指出，对于工作在恒流状态下的电弧，Mayr 模型和Cassie 模型中的参数P0、E0与气流量m 之间的关系可用式（7）和式（8）表示，式中n1、n2 为常数。

设某一时刻P0=0ˆP ，E0=0ˆE ，m=m0，根据式（7） 和式（8），当气流量为m 时，有如下表达式：

将式（9）、式（10）代入式（2）、式（3），经整理，则Mayr 模型和Cassie 模型可分别表示为

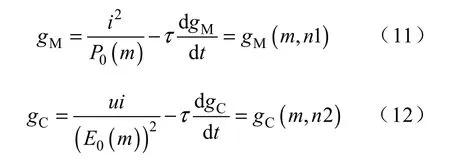
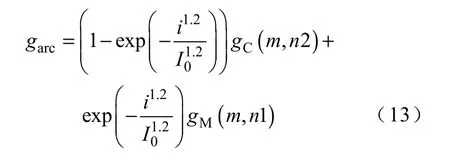
由此可得本文提出的电弧模型为 其中，参数P0、E0、I0以及系数n1、n2 的选取与电弧加热器结构、气体介质、功率大小等因素有关，它们的确定方法将在下文中结合电弧加热器电源系统模型实现具体讨论。

3 电弧模型在Matlab 中的实现

3.1 电弧加热器电源系统模型

等离子电弧具有U 形伏安特性曲线，为了保证电弧有一个稳定的工作点，电弧供电电源应具备垂直陡降的外特性。本文中，电弧加热器电源为一个经PI 调节恒流输出的18 脉晶闸管全控整流电源，该电源由三个6 脉晶闸管全控整流桥经移相变压器移相串联而成，以减少谐波并获得高压。其控制框图如图3 所示。

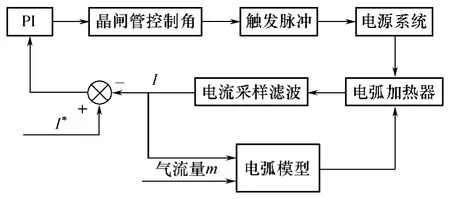
图3 电弧加热器电源系统控制框图 Fig.3 Control scheme of arc heater power supply system

该电弧加热器电源系统在 Matlab/Simulink 中建模实现。其中，每个移相变压器之间的角度相差 20°，电弧模块是由S 函数控制且符合欧姆定律的可控电压源，用于表示动态的电弧电阻Rarc。S 函数是根据式（13）编写的。其中电弧电流由电流传感器直接在电路中测得，电弧电压根据欧姆定律在每次电弧阻值发生变化后更新并反馈给S 函数，参与下一采样周期电弧电阻值及电弧电压值的计算。为了消除仿真算法可能引起的代数环问题，每个变量必须通过存储模块再反馈到S 函数中。

3.2 电弧模型参数的确定

模型中参数的正确选取对模型的准确性有着重要的意义。为了能更好地确定各参数大小，首先考察各参数对模型的影响。首先，用一个幅值可从零到某一较大值变化的可控直流电压源代替恒流电压源给电弧负载供电，以获得电弧模型的静特性曲线。其次，在保持其他参数值不变的情况下，通过改变某一模型参数的大小，得到不同的静特性曲线，以考察该参数对电弧模型的影响。

设初始条件为P0=106W，E0=3000V，I0=2000A，τ =0.0001s，m=160g/s，分别改变P0、E0和I0，得到图4～图6 所示三组曲线簇。

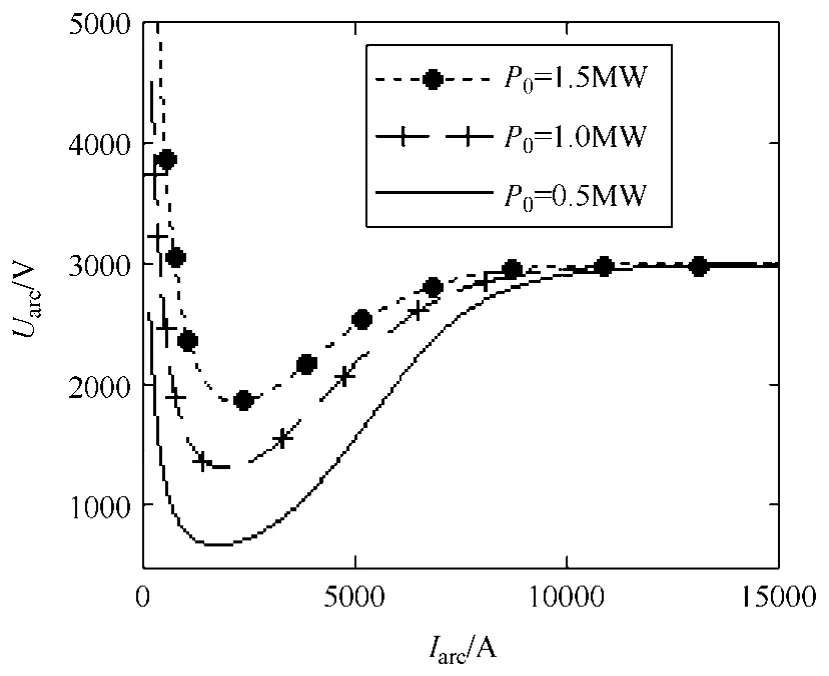
图4 P0 对电弧静态曲线的影响 Fig.4 Effect of P0 on U-I characteristic curve

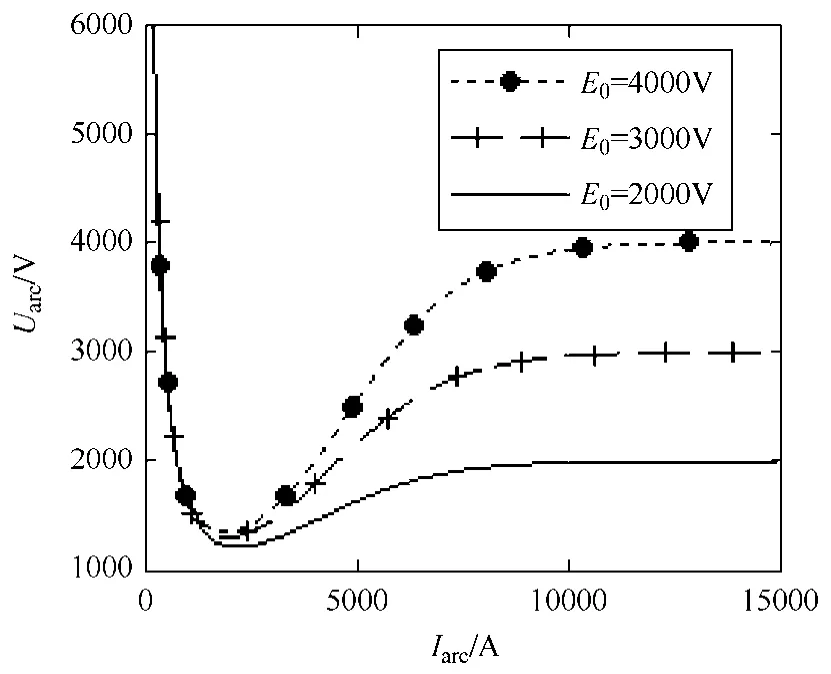
图5 E0 对电弧静态曲线的影响 Fig.5 Effect of E0 on U-I characteristic curve

图6 I0 对电弧静态曲线的影响 Fig.6 Effect of I0 on U-I characteristic curve

从这三组曲线簇中，可得到如下结论：

（1）小电流区电弧静特性曲线呈双曲线分布，电弧表现为负阻，即电弧电压随着电弧电流的上升而下降。电弧静特性曲线的位置主要受P0影响，当P0增大时，小电流区的静态曲线也随之上移。

（2）大电流区电弧静特性曲线呈上升趋势，电弧表现为正阻，即电弧电压随着电弧电流的上升而上升。电弧静特性曲线的位置主要受 E0影响，当 E0增大时，大电流区的静态曲线也随之上移。

（3）I0决定了小电流向大电流过渡的区域，I0越大，过渡区域越后移，且较为平坦。

根据实际应用情况改变P0、E0、I0大小，即可调整电弧静特性曲线位置，得到需要的电弧模型。对于参数τ，经多次仿真比较并参考文献[7，12]，对于工作在电流大于1000A 的电弧，τ 可视为常数，取τ =0.0001s。对于气流量m 的上标n1、n2，首先固定某一个气流量m，通过与实验测得的电弧静特性曲线比较，确定P0、E0、I0的值。然后加入气流量变化，根据仿真结果确定n1、n2 的值，得到合适的电弧模型。

4 仿真结果与实验结果

当气流量为m=112g/s 时，电弧模型与实验数据的静特性曲线拟合如图7 所示，其中“×”为实验数据，“—”为仿真模拟电弧静特性曲线。此时P0= 8.5×105W，E0=6000V，I0=2200A。

当电弧加热器稳定工作时，模型仿真结果与实验结果比较见下表，其中n1=n2=0.33。

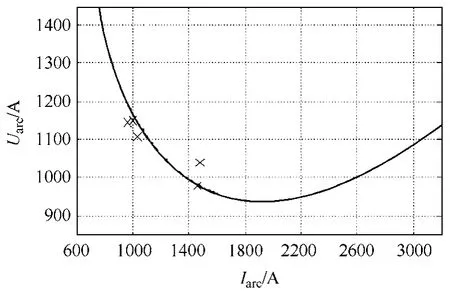
图7 m=112g/s 时，电弧模型静特性曲线拟合 Fig.7 U-I characteristic curve fitting when m=112g/s

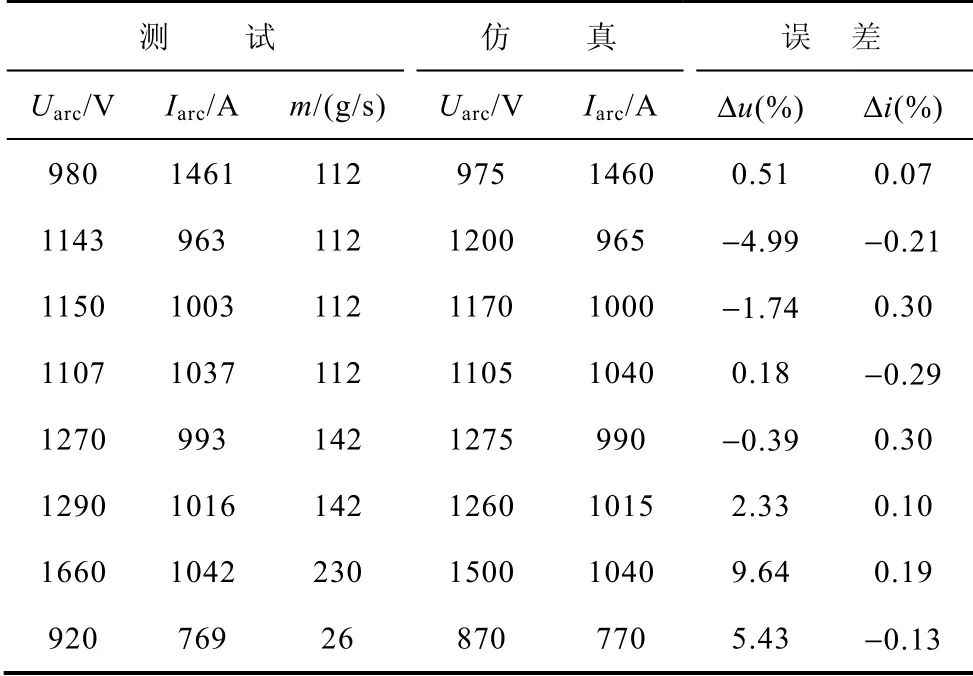
表 仿真结果与实验结果对比 Tab. Comparison between simulated and experimental results

当气流量发生扰动时，如在1s 时突降，0.3s 后恢复，此时电弧电压、电弧电流以及电弧阻值波形如图8 所示。

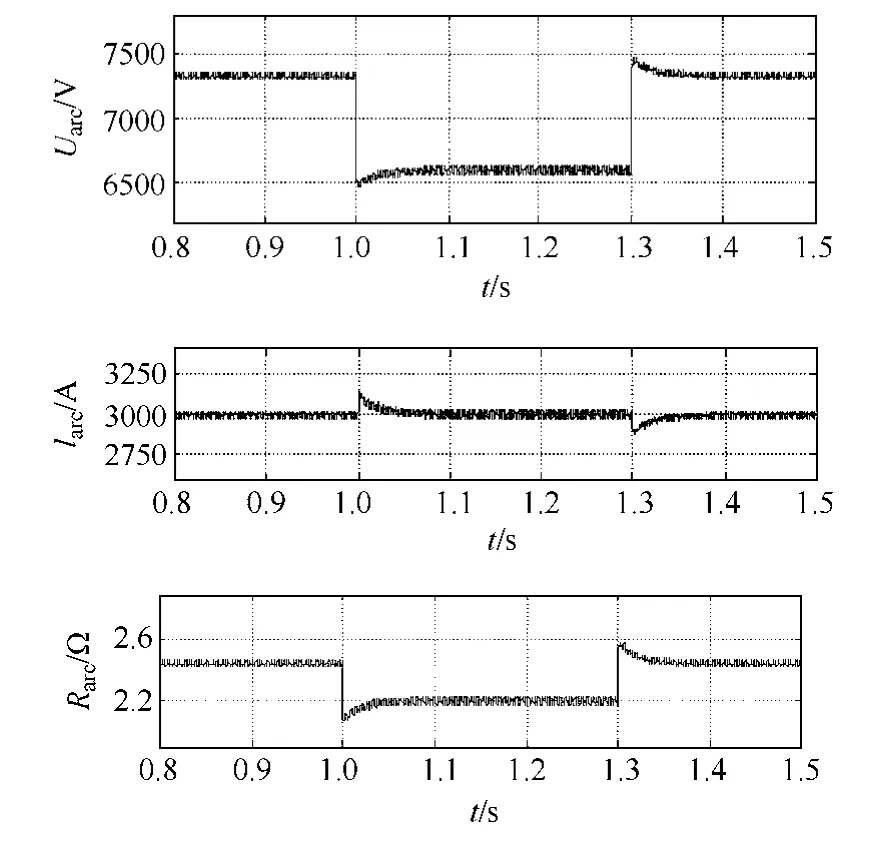
图8 气流量发生扰动时电弧电压、 电流、电弧阻值的波形 Fig.8 Waveforms of arc voltage,current and resistance when mass flowrate disturbed

当气流量突减时，电弧中等离子运动速度减小，电弧电压降低。但是由于电流环PI 调节的缘故，电源保持恒流输出，电弧电流不变，电弧电阻值减小，这与上述波形描述的情况一致。

项目实测的电弧电压、电流波形如图9 所示。图10 为对应的电弧电压和电弧电流仿真波形。

图9 电弧电压、电流的实测波形 Fig.9 Experimental waveforms of Uarc,Iarc

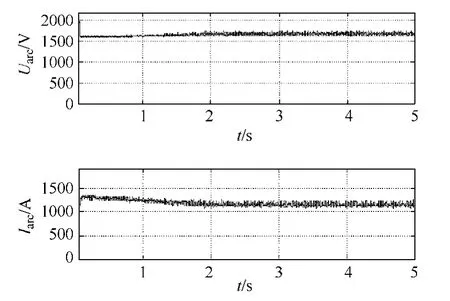
图10 电弧电压、电流的仿真波形 Fig.10 Simulated waveforms of Uarc,Iarc

由上述波形及数据对比可知，本文所述的电弧模型具有较高的准确性，且能较好地描述实际电弧的动态特性和静态特性。

5 结论

本文分析了Cassie 电弧模型和Mayr 电弧模型，并在这两个模型的基础上，提出了一种适用于直流大功率电弧加热器的等离子电弧模型。该模型加入了气流量参数，使模型能直接反映气流量对电弧工作的影响。同时，本文就Cassie 电弧模型和Mayr电弧模型之间的过渡函数的选取进行了讨论分析，并介绍了模型参数的确定方法，使该模型能通过简单调整，适用于不同电弧应用场合。最后，通过在Matlab 中建模仿真，模拟了大功率电弧加热器的工作情况。仿真与实测数据的比较结果表明，该模型能较为准确地描述电弧的动态和静态特性，为电弧加热器电源系统的深入研究打下基础。

[1] 李兴文,陈德桂.空气开关电弧的磁流体动力学建模及特性仿真[J].中国电机工程学报,2007,27(21),31-37.

Li Xinwen,Chen Degui.Magnetohydrodynamics modeling and characteristics simulation of air switching arc[J].Proceedings of the CSEE,2007,27(21):31-37.

[2] Blais A,Proulx P,Boulos M I.Three-dimensional numerical modelling of a magnetically deflected dc transferred arc in argon[J].Journal of Physics D:Applied Physics,2003,36(5):488-496.

[3] 吴建全.直流电弧负载模拟及其控制方法研究[D].西安:西安理工大学,2004.

[4] Amato F,Mattei M,Pironti A.Robust control of a power supply system for an arc heater[C].Proceeding of the 1996 IEEE International Conference on Control Applications,1996:882-887.

[5] Guardado J L,Maximov S G,Melgoza E,et al.An improved arc model before current zero based on the combined Mayr and Cassie arc models[J].IEEE Transactions on Power Delivery,2005,20(1):138- 142.

[6] 臧春艳.航天继电器稳态电弧等离子体电离过程与电弧特性研究[D].武汉:华中科技大学,2006.

[7] Tseng K J,Wang Y,Vilathgamuwa D M.Development of a dynamic model of electric arc for power electrics simulations[C].Proceeding of IEEE 31th IAS Annual Meeting on Industry Applications,1996,4:2173- 2180.

[8] 李德元,赵文珍,董小强,等.等离子技术在材料加工中的应用[M].北京:机械工业出版社,2005.

[9] Suh Y,Lee Y,Kheir J,et al.A study on medium voltage power conversion system for plasma torch[C].Proceedings of IEEE Power Electron.Spec.Conf.,2008:437-443.

[10] 郭文杰.航天器大气环境模拟用高压大功率电弧加热器电源系统研究[D].北京:北京交通大学,2008.

[11] Zhilinskii O V,Laktyushina T V,Laktyushin A N.Multicriterial optimization of the operation and design parameters of electric-arc plasmatrons of linear circuits[J].Engineering Physics and Thermo- physics,2002,75(6):1278-1282.

[12] Suh Y,Lee Y,Lee Yongjoong,et al.A comparative study of medium-voltage power converter topologies for plasma torch under dynamic operating conditions[J].IEEE Transactions on Industrial Electronics,2009,56(6):2150-2161.