基于直流偏磁实验的叠片铁心磁化特性分析

赵小军 李 琳 程志光 鲁君伟 卢铁兵 刘兰荣 范亚娜

(1.华北电力大学电气与电子工程学院 保定 071003 2.保定天威集团技术中心 保定 071056 3.格里菲斯大学格里菲斯工程学院 布里斯班 4111)

1 引言

变压器绕组中直流或准直流电流的出现是导致变压器直流偏磁的直接原因。绕组中存在的直流电流会使变压器铁心中存在相应的直流磁动势和直流磁通[1]，直流磁通与交流磁通相叠加，造成铁心的迅速饱和，从而对变压器和电网运行性能产生严重的危害。变压器绕组中直流或准直流电流出现的原因，主要有以下几个方面[2-3]：①太阳黑子活动时产生的太阳风暴；②高压直流输电采用的单极大地回线和双极不平衡回线运行方式；③交直流输电线路并行运行。

有多种计算方法用于直流偏磁问题的研究。磁路法[4-6]模型简单便于实现，主要用于励磁电流的谐波分析和简单的磁场分析；电磁场有限元法[7-9]用于直流偏磁磁场的准确计算及损耗特性的分析[10-11]。上述用于研究直流偏磁问题的各种数值方法均采用无偏磁磁化曲线进行计算，即认为直流偏磁条件下材料的磁化特性并没有发生变化。然而相关的实验研究[12-14]表明，直流偏磁条件下铁磁材料的交流磁滞回线与无偏磁情况相比，发生了明显的改变。因此可知直流偏磁磁化曲线也必然与无偏磁磁化曲线不同。获得准确的直流偏磁磁化曲线，深入分析铁磁材料在直流偏磁条件下的磁化特性，将使基于各种数值方法的计算结果更加准确，从而有助于直流偏磁问题的研究和解决。

要获得铁磁材料的直流偏磁磁化特性，直流磁通的准确计算十分关键。本文以叠片铁心模拟变压器铁心的实际工作状态，利用改进迭代法准确预测铁心中的直流磁通，对叠片铁心的直流偏磁磁化特性进行了详尽地分析。从工程实用的角度出发，提出模拟直流偏磁磁滞特性的数值方法，并研究了直流偏置量对铁心损耗的影响。

2 直流磁通的计算

2.1 简单迭代法存在的问题

直流偏置量的施加使铁心中存在相应的直流磁通，而直流磁通最直接地反映了叠片铁心真实的直流偏置水平。深入研究直流偏磁下叠片铁心的磁化特性和损耗特性，要求准确求解铁心中的直流磁通。受目前实验条件的限制，叠片铁心中的直流磁通和直流磁通密度难以由实验测量直接得到。

简单迭代法[15-16]是目前计算直流磁通时普遍采用的方法。该方法基于无偏磁下的i−ϕ 基本磁化曲线对直流磁通进行计算，将计算的励磁电流与测量值作比较，当Epeak（励磁电流峰值的计算值与测量值间的误差）和Edc（励磁电流直流分量的计算值与测量值间的误差）均小于5%时，即认为此时的直流磁通为直流偏磁条件下的直流磁通。然而这种方法在应用过程中存在着如下问题：当外加交流电压较低时，励磁电流峰值误差 Epeak和直流分量误差Edc不能同时控制在5%以内，尤其当交流电压较高时，此时励磁电流的负峰值出现，励磁电流峰值误差和直流分量误差均大于10%。在这种误差标准下计算得到的直流磁通，显然是不够准确的，由此得到的直流偏磁下的磁滞回线和基本磁化曲线也将与实际的曲线存在较大的误差。造成简单迭代法计算误差的原因主要有两点：一是简单迭代法未考虑磁滞效应，导致由此计算出的励磁电流与实际的励磁电流之间存在误差。二是简单迭代法采用的无偏磁下的基本磁化曲线对偏磁下的直流磁通进行预测，但直流偏磁条件下的磁化曲线与无偏磁条件下的磁化曲线在局部存在着较大的差异。

要得到准确的直流磁通和直流磁通密度，首先要在迭代法中考虑磁滞效应。其次要对迭代法中使用的基本磁化曲线不断进行修正。对于磁滞的模拟，可以考虑目前已有的磁滞模型，如J-A 磁滞模型[17]和Preisach 磁滞模型等，但这些方法都需要与各种优化算法[2]相结合，不仅需要较大的数据量和计算量，而且算法实现较为复杂，从满足工程精度的角度出发，可以采用易于实现且能够达到足够精度的方法。

2.2 改进迭代法

在无偏磁条件下，由于磁滞效应，在励磁电流的前半个周期内，前1/4 周期与后1/4 周期的波形并不对称。考虑到励磁电流与磁通、感应电动势之间的关系，可以将励磁电流i 分为两部分，一部分与磁通ϕ 同相位，一部分与感应电动势e 同相位[18]。于是，在i−ϕ 关系中可以引入以下函数（其中ϕ′为磁通ϕ 的导数）： 式中，函数f1是仅基于中间磁化曲线（i−ϕ 磁滞回线的中点轨迹）获得的i−ϕ 关系[19]，称之为无损耗函数。函数 f2对应的是磁滞损耗，称之为损耗函 数[19]。

在直流偏磁条件下，同样引入如式（1）所示的i−ϕ 关系。则f1对应于直流偏磁下的中间磁化曲线（i−ϕ 直流偏磁磁滞回线的中点轨迹），由于中间磁化曲线过磁滞回线的顶点，当磁滞回线足够密集时，可以将各磁滞回线顶点的连线近似作为中间磁化曲线。对损耗函数f2作如下定义：在基于i−ϕ 关系的直流偏磁磁滞回线中，交流磁通ϕac为零时对应的励磁电流有两个值，将二者的绝对值取平均并记为Iob[19]，则损耗函数与磁通存在如下关系：

式中 ϕ—总磁通；

ϕm—交流磁通ϕac的幅值；

ϕdc—直流磁通。

基于以上分析，采用新的迭代法对叠片铁心中的直流磁通和直流磁通密度进行计算，步骤如下：

（1）在某一直流偏磁条件下，基于无偏磁下的基本磁化曲线，利用简单迭代法获得不同交流激励下的直流磁通ϕdc。

（2）计算直流偏磁条件下的交流磁通ϕac。对测量得到的端口感应电动势e 进行积分得到相应的交流磁通ϕac（N 为线圈匝数）

将步骤（1）中计算的直流磁通ϕdc与交流磁通ϕac相叠加得到总磁通ϕ，又由测量得到的励磁电流i，可得到基于 i−ϕ 关系的直流偏磁磁滞回线，连接各条回线的顶点，得到修正的直流偏磁基本磁化曲线，相对于步骤（1）中无偏磁下的基本磁化曲线，该曲线更加接近于实际的直流偏磁基本磁化曲线。

（3）由步骤（2）中得到的修正后的直流偏磁基本磁化曲线可以确定函数f1，由步骤（2）中得到的各直流偏磁磁滞回线，可以确定相应的Iob和函数f2。结合式（2）对直流磁通ϕdc进行调整并计算相应的励磁电流，当Epeak和Edc均在5%以内且同时达到最小时，即可确定为修正后的直流磁通。

3 直流偏磁实验与改进迭代法的验证

3.1 叠片铁心的直流偏磁实验

基于保定天威集团制造的产品级叠片铁心，进行了不同偏磁条件下的直流偏磁实验。叠片铁心模型如图1 所示，铁心上绕有两组线圈，分别为励磁线圈和测量线圈，在励磁线圈两端施加交流电压，直流偏置量则以直流电流的形式施加。实验电路图及实验设备说明可参考相关文献[8]。

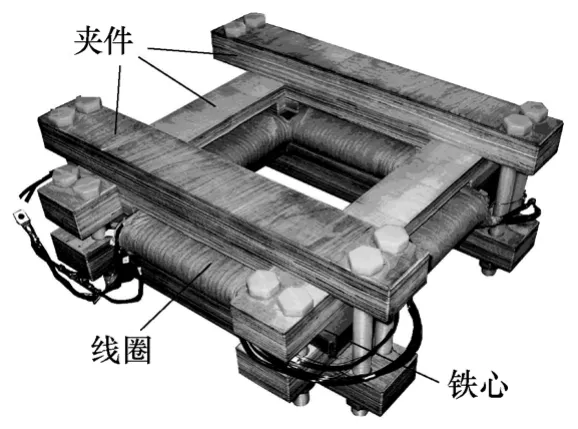
图1 叠片铁心模型 Fig.1 The laminated core model

为定量研究叠片铁心的直流偏磁特性，需要选定直流电流的基准值。在本实验中，选择无偏磁条件下铁心内额定磁通密度（1.7T）对应的励磁电流峰值作为直流偏置量的基准值。在针对叠片进行的实际测量中，得到的直流偏置量基准值I0为1.68A。

叠片铁心中磁通密度B 和磁通ϕ，励磁电流i和磁场强度H 之间存在如下关系：

式中 S—叠片铁心的有效截面积；

L—叠片铁心的等效磁路长度；

N—励磁线圈匝数。

由于叠片铁心中存在的以上关系，在研究i−ϕ关系的同时，可以得到基于B-H 关系的叠片铁心磁化特性。

在直流偏磁实验中，直流偏置电流Idc按照基准值的不同比例依次施加，分别为25% I0，50% I0，75% I0和100% I0，相应的直流偏置磁场强度Hdc分别为107A/m、213A/m、320A/m、427A/m。当直流偏置量固定时，逐步增加交流电压，获得不同交流激励下的励磁电流波形数据。不失一般性，本文针对Hdc=107A/m 和Hdc=213A/m 两种直流偏磁情况进行了详细分析。

3.2 利用改进迭代法计算直流磁通

在不同偏磁条件下，将改进迭代法与简单迭代法的计算结果进行比较，以验证改进迭代法的有效性。由表1、表2 可以看出，在交流磁通密度Bac较大和较小时，简单迭代法的计算误差均较大，在利用了改进迭代法后，可将Epeak和Edc同时控制在5%以内，计算误差明显减小，此时计算得到的直流磁通密度更加准确。图 2 给出了 Hdc=107A/m，Bac=1.7454T 时，两种迭代法计算的励磁电流与实测励磁电流的比较。图3 为基于改进迭代法计算得到的磁滞回线与测量曲线的比较。

表1 Hdc=107A/m 时计算结果的比较 Tab.1 Comparison of the calculated results (Hdc=107A/m)

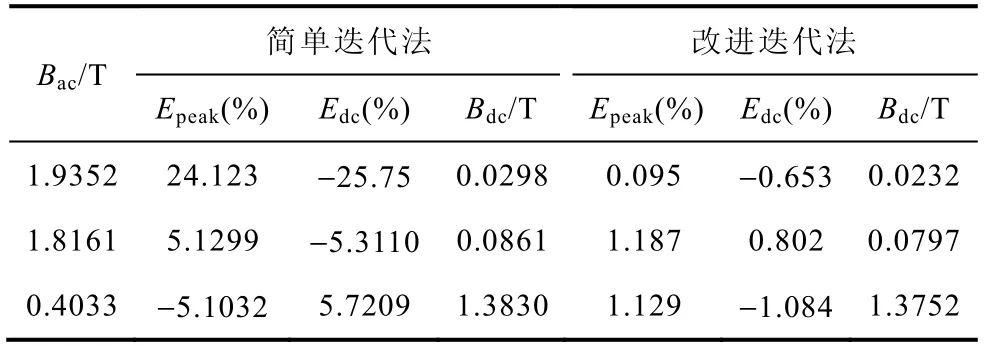
表2 Hdc=213A/m 时计算结果的比较 Tab.2 Comparison of the calculated results (Hdc=213A/m)

图2 励磁电流计算结果与测量结果的比较 Fig.2 Comparison between calculated and measured magnetizing currents

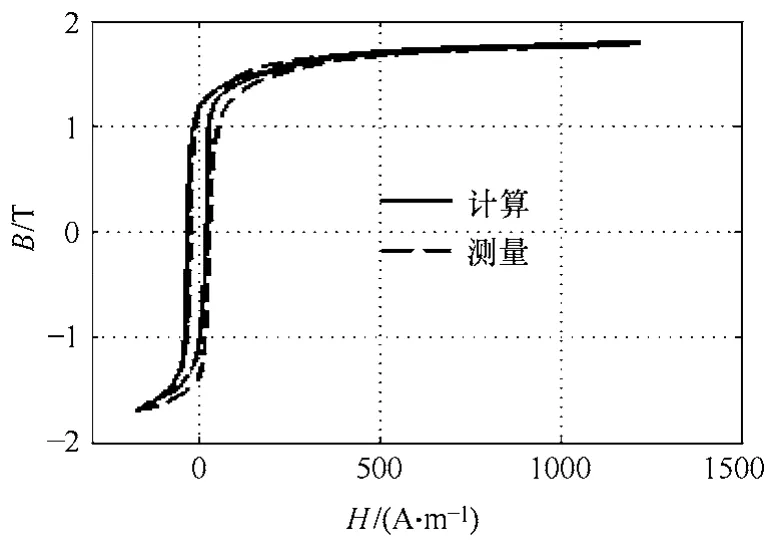
图3 偏磁条件下磁滞回线计算值与实验值的比较 Fig.3 Comparison between the calculated and measured DC-biasing hysteresis loops

在满足工程精度的要求下，可将简单迭代法和改进迭代法结合使用。以简单迭代法为主，当Epeak和Edc均大于5%时，使用改进迭代法对直流磁通进行修正；在实际计算中，无偏磁磁化曲线经过一次修正后即可得到较为准确的直流偏磁磁化曲线。上述方案可以在保证工程精度的前提下有效地减少计算量。

4 直流偏磁下的磁滞回线和基本磁化曲线

由第3 节中的直流偏磁实验和计算结果可知，利用改进迭代法计算得到的直流磁通更加准确。将最终计算得到的直流磁通ϕdc与由式（3）得到交流磁通ϕac相叠加，即可得到基于i−ϕ关系的直流偏磁磁滞回线。由于直流磁通ϕdc是比较准确的，而交流磁通ϕac和励磁电流i 均是基于测量结果得到的，因此可以认为此时的直流偏磁磁滞回线与实际的直流偏磁磁滞回线十分接近。

为了研究直流偏磁条件下叠片铁心磁滞回线和基本磁化曲线的特性，图 4 给出了直流磁场强度Hdc=107A/m 时的直流偏磁磁滞回线族。由图4 可知，与无偏磁条件下的磁滞回线不同，直流偏磁条件下的各磁滞回线在第一、三象限不再对称。这是无偏磁下的各磁滞回线沿B＞0 和H＞0 方向同时移动的结果（与Bdc＞0 相对应）。

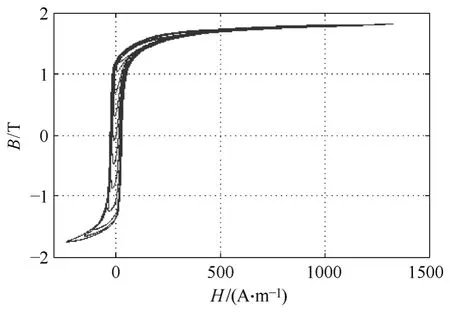
图4 Hdc=107A/m 时的直流偏磁磁滞回线 Fig.4 DC-biasing hysteresis loops (Hdc=107A/m)

将图4 中各磁滞回线的顶点相连接，得到直流偏磁条件下的基本磁化曲线。图5 和图6 对无偏磁条件下和有偏磁条件下的基本磁化曲线进行了比较。为了更好地观察偏磁条件下基本磁化曲线的变化，在图5 中，对磁场强度H 采用了对数坐标。由图可知，直流偏磁条件下的基本磁化曲线与无偏磁下的基本磁化曲线存在着明显的差异。在磁场强度H＞0 的线性区域，当磁场强度相同时，偏磁下的磁化曲线对应的磁感应强度值大于无偏磁曲线对应的磁感应强度值，这主要是由直流磁通造成的。在非线性饱和区，由于直流磁通的迅速减小，两条曲线的走向趋于一致。图6 则比较了磁场强度H＜0 时的各条基本磁化曲线。可以看出在磁场强度小于零时，有无偏磁条件下的基本磁化曲线也同样存在着差异。在磁场强度接近于零的区域，偏磁下的磁化曲线不再通过原点，且随着直流偏置量的增大而被不断抬高。而在非线性区域，偏磁下的磁化曲线则很快进入饱和区。

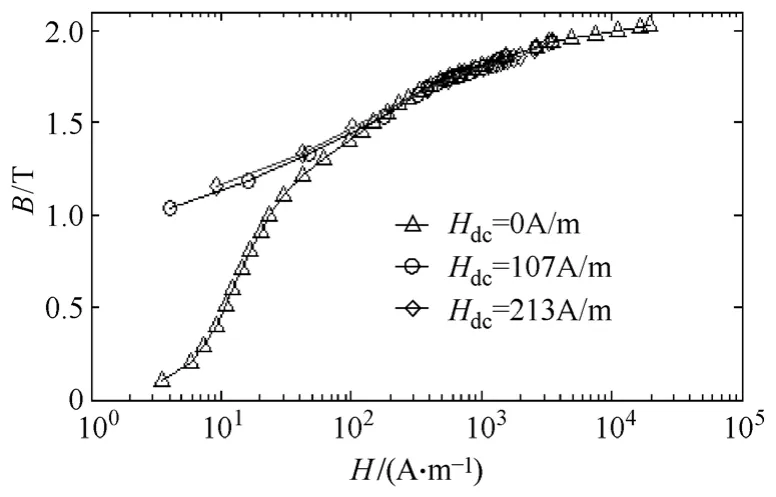
图5 H＞0 时有无偏磁条件下基本磁化曲线的比较 Fig.5 Comparison between the normal magnetizing curves with DC bias and without DC bias (H＞0)

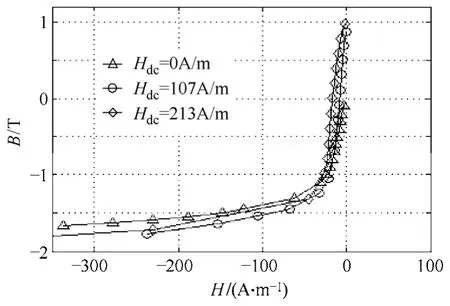
图6 H＜0 时有无偏磁条件下基本磁化曲线的比较 Fig.6 Comparison between the normal magnetizing curves with DC bias and without DC bias (H＜0)

以上有无偏磁条件下基本磁化曲线的差异，正是基于无偏磁基本磁化曲线的简单迭代法计算直流磁通时，在磁场强度接近于零的正负区域内产生较大误差的原因。

由直流偏置磁场的性质可知，若将施加于叠片铁心的直流偏置量反向，则直流磁通反向，新的直流偏磁下的磁滞回线和基本磁化曲线将分别与原来的曲线关于原点对称。

5 直流偏磁磁滞回线的准确模拟与铁损的计算

直流偏磁磁滞回线的准确模拟对于叠片铁心磁化特性和损耗特性的研究具有重要的意义。因此在得到直流偏磁磁滞回线的同时，还需要考虑对其进行基于数学或物理模型的准确模拟。

第2 节的改进迭代法中提出了基于中间磁化曲线和损耗函数的i−ϕ 磁滞模型。但式（2）中所采用的损耗函数仅是考虑直流偏磁条件下磁滞损耗的一种简化方法。此时的损耗函数虽然容易确定，但从图3 可以看出，由此得到的磁滞回线与测量曲线仍有一定的误差，因此还不能满足准确模拟直流偏磁磁滞回线的要求。为实现对直流偏磁条件下的i−ϕ 磁滞回线的准确拟合，可对损耗函数作如下定义[20]：

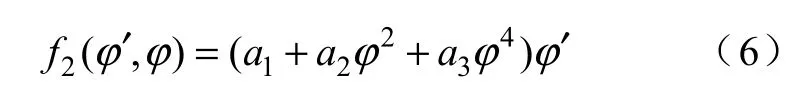
式中，a1、a2、a3为相关系数，磁通ϕ 定义如下：

根据式（1），总的励磁电流i 可以表达为如下形式：

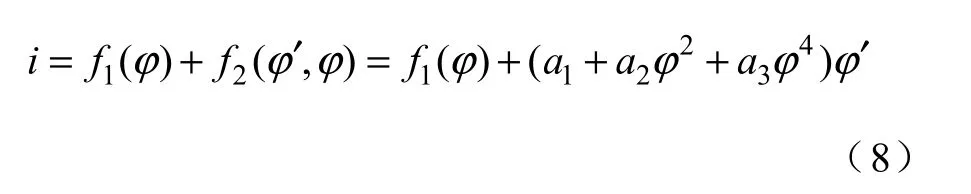
为引入直流磁通的影响，当交流磁通为零时存在如下关系：

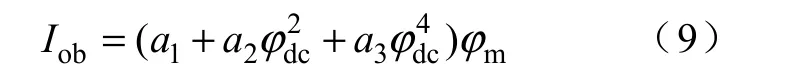
式中的Iob与式（2）中的意义相同。将N 组测量数据代入到式（8），得

利用最小二乘法，将式（10）中各式整理后平方相加，对a2和a3求导，再与式（9）联立，可以解得损耗函数中的各项系数。将各项系数代入到式（8），即可得到损耗函数f2。函数f1则与中间磁化曲线相对应。将二者相加即为直流偏磁条件下励磁电流i的解析表达式。由式（4）和式（5）所示的叠片铁心中磁通密度与磁通，励磁电流与磁场强度间的关系，可以得到直流偏磁下的B-H 磁滞回线。

为验证该方法的有效性，对偏磁条件下的磁滞回线进行拟合。图7 为拟合曲线与测量曲线的比较，图8 为相应的励磁电流计算值与测量值的比较。由图可知，拟合得到的磁滞回线与实际测量得到的磁滞回线吻合较好。

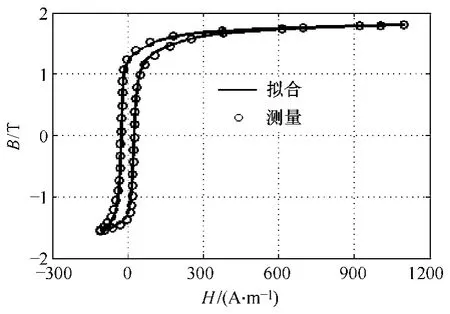
图7 直流偏磁磁滞回线拟合结果与测量结果的比较 Fig.7 Comparison between fitted and measured DC-biasing hysteresis loop

根据以上方法求出的i−ϕ 关系，可以计算直流偏磁条件下的叠片铁心损耗。

式中，f 为频率。

由于式（8）中的励磁电流i 由无损耗函数f1和损耗函数f2构成，f1对应的铁心损耗为零，因此可以直接对损耗函数f2进行积分得到直流偏磁条件下叠片铁心的损耗[21]

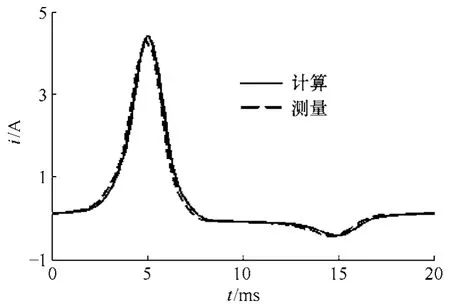
图8 励磁电流计算值与测量值的比较 Fig.8 The comparison between calculated and measured magnetizing current

表3 比较了不同偏磁条件下叠片铁损的计算值与测量值。其中Pc为损耗的计算值，Pm为损耗的测量值。可以看出，二者的误差很小，这进一步说明了利用以上方法对直流偏磁磁滞回线进行拟合的准确性。同时可以发现，有偏磁下的叠片铁损大于无偏磁下的铁损，且损耗值随直流偏置量的增大而增大。

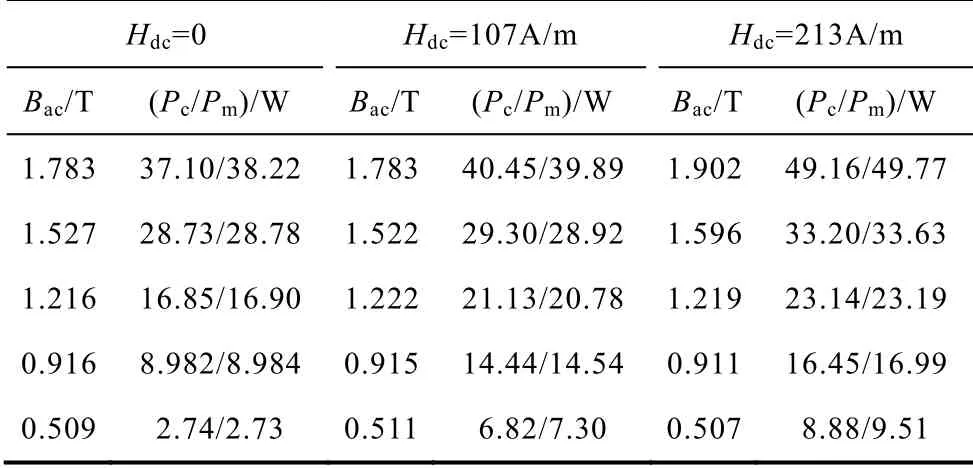
表3 不同偏磁条件下铁损计算值与测量值的比较 Tab.3 Comparison between the calculated and measured core loss under different DC bias condition

6 结论

直流偏磁条件下，铁心中直流磁通的计算和叠片铁心磁滞特性的模拟是研究变压器直流偏磁问题的关键。改进迭代法引入损耗函数，将其与无损耗函数相加模拟直流偏磁磁滞效应，通过不断修正磁化曲线对直流磁通进行准确地预测。励磁电流计算结果与测量结果的误差小于5%，证明该方法的准确性和有效性。基于叠片铁心的直流偏磁实验，得到了非对称的直流偏磁磁化曲线；分析了不同偏置量对直流偏磁磁化特性的影响，并对直流偏磁磁滞回线进行准确的拟合。测量与计算结果表明，在交流激励一定时，直流偏置量的增大将导致铁损的增加。

在直流偏磁条件下，叠片铁心的磁化特性和损耗特性均发生了明显的变化，基于直流偏磁磁化曲线的数值计算在直流偏磁问题的研究中十分必要。

[1] 李慧奇,崔翔,侯永亮,等.直流偏磁下变压器励磁电流的实验研究及计算[J].华北电力大学学报,2007,34(4):1-6.

Li Huiqi,Cui Xiang,Hou Yongliang,et al.Experimental studies and calculation of the exciting current in the transformer under DC bias magnetization[J].Journal of North China Electric Power University,2007,34(4):1-6.

[2] 赵志刚,刘福贵,张俊杰,等.直流偏磁条件下变压器励磁电流的实验与分析[J].电工技术学报,2010,25(4):71-76.

Zhao Zhigang,Liu Fugui,Zhang Junjie,et al.Measurement and analysis of magnetizing current in DC-biased transformers[J].Transactions of China Electrotechnical Society,2010,25(4):71-76.

[3] 曾嵘,唐剑,张波,等.交直流输电线路并行对换流变的直流偏磁影响及对策[J].陕西电力,2008,36(9):1-5.

Zeng Rong,Tang Jian,Zhang Bo,et al.Effect of parallel AC/DC transmission line upon DC bias of converter transformer & its countermeasure[J].Shan Xi Electric Power,2008,36(9):1-5.

[4] 皇甫成,魏远航,钟连宏,等.基于对偶性原理的三相多芯柱变压器暂态模型[J].中国电机工程学报,2007,27(3):83-88.

Huangfu Cheng,Wei Yuanhang,Zhong Lianhong,et al.A transient model of three phase multi-legged transformer based on duality theory [J].Proceedings of the CSEE,2007,27(3):83-88.

[5] 李晓萍,文习山.三相五柱变压器直流偏磁计算研究[J].中国电机工程学报,2010,30(1):127-132.

Li Xiaoping,Wen Xishan.DC bias computation study on three phase five limbs transformer[J].Proceedings of the CSEE,2010,30(1):127-132.

[6] 李泓志,崔翔,卢铁兵,等.变压器直流偏磁的电路−磁路模型研究[J].中国电机工程学报,2009,29(27):119-125.

Li Hongzhi,Cui Xiang,Lu Tiebing,et al.Research on the electric circuit and magnetic circuit combined model of DC biased power transformer[J].Proceedings of the CSEE,2009,29(27):119-125.

[7] 姚缨英.大型电力变压器直流偏磁现象的研究[D].沈阳:沈阳工业大学,2000.

[8] 赵小军,李琳,程志光,等.应用谐波平衡有限元法的变压器直流偏磁现象分析[J].中国电机工程学报,2010,30(21):103-108.

Zhao Xiaojun,Li Lin,Cheng Zhiguang,et al.Analysis of the DC bias phenomenon in transformers based on harmonic-balanced finite element method [J].Proceedings of the CSEE,2010,30(21):103-108.

[9] Biro O,Ausserhofer S,Buchgraber G.Prediction of magnetizing current waveform in a single-phase power transformer under DC bias[J].Institution of Engineering and Technology,Science,Measurement and Technology,2007,1(1):2-5.

[10] 程志光,高桥则雄,博扎德· 弗甘尼.电气工程电磁热场模拟与应用[M].北京:科学出版社,2009.

[11] 赵志刚.电力变压器直流偏磁问题的工程模拟[D].天津:河北工业大学,2010.

[12] 刘硕,刘志强,刘福贵,等.交直流叠加磁化特性的测量及具有直流偏磁磁场的数值分析[J].河北工业大学学报,2000,29(6):22-26.

Liu Shuo,Liu Zhiqiang,Liu Fugui,et al.Measurement of AC&DC superposition magnetization characteristic and analysis of magnetic field with DC bias[J].Journal of Hebei University of Technology,2000,29(6):22-26.

[13] 王永,刘硕.具有直流偏磁交流磁滞回线的测量[J].磁性材料及器件,2001,32(3):47-50.

Wang Yong,Liu Shuo.The measurement of AC hysteresis loop with DC magnetic biasing[J].Journal of Magnetic Materials and Devices,2001,32(3):47-50.

[14] 曹华贵.爱泼斯坦方圈测电工钢片直流偏磁性能方法研究[J].中国制造业信息化,2009,38(11):40-43.

Cao Huagui.Research on the magnetic properties of electric steel sheet with DC magnetic field based on Epstein frame[J].Manufacture Information Engineer- ing of China,2009,38(11):40-43.

[15] 王祥珩,徐伯雄.变压器的偏磁问题[J].变压器,1992,29(8):11-14.

Wang Xiangheng,Xu Boxiong.The problems on biased transformer[J].Transformer,1992,29(8):11-14.

[16] 郭满生,梅桂华,刘东升,等.直流偏磁条件下电力变压器铁心B-H 曲线及非对称励磁电流[J].电工技术学报,2009,24(5):46-52.

Guo Mansheng,Mei Guihua,Liu Dongsheng,et al.B-H curve based on core and asymmetric magnetizing current in DC-biased transformers[J].Transactions of China Electrotechnical Society,2009,24(5):46-52.

[17] 曹林,何金良,张波,等.直流偏磁状态下电力变压器动态磁滞损耗模型及验证[J].中国电机工程学报,2008,28(24):141-146.

Cao Lin,He Jinliang,Zhang Bo,et al.Dynamic hysteresis loss model of power transformer under DC current biasing and its verification[J].Proceedings of the CSEE,2008,28(24):141-146.

[18] Kulkarni S V,Khaparde S A.Transformer engineering:design and practice[M].New York:Marcel Dekker,2004.

[19] Lin C E,Wei J B,Huang C L,et al.A new method for representation of hysteresis loops[J].IEEE Trans- actions on Power Delivery,1989,4(1):413-420.

[20] Faiz J,Sharifian M.Hysteresis loop modeling techniques and hysteresis loss estimation of soft magnetic materials[J].COMPEL,2001,20(4):981- 1001.

[21] 邹继斌,刘宝廷,崔淑梅,等.磁路与磁场[M].哈尔滨:哈尔滨工业大学出版社,1997.