基于移动荷载分析的沥青路面结构优化设计

张大明， 卜建清

( 石家庄铁道大学 土木工程学院，河北 石家庄 050043)

目前对于沥青路面的研究已经不是简单的静力荷载分析，更多的时候要考虑作用在路面上的无规律性、瞬时性以及非线性的动荷载作用［1］。计算中采用移动加载能够较好地模拟真实行车荷载空间位置随时间变化而不断变化的特点，对于路面力学行为的分析也就更加准确。

影响路面使用性能与力学性能的因素是多方面的，所以路面材料的性能参数也很多。国内外学者们从路面层状体系受力的角度，采用单因素分析法进行分析，并做了大量的研究工作，取得一些成果，但这种方法难免存在一定的片面性。现基于正交分析理论，综合分析各因素的改变对于路面结构受力的影响，然后根据理论知识和实际经验，对各指标的分析结果进行综合比较和分析，以最大限度的降低路面结构层动力响应为目标优化路面结构设计，得到各层参数的最佳组合［2］。

1 计算车型、路面结构参数的选取

额定载荷为25．4 kN，相应胎压630 kPa，双轮最小中心距346 mm，胎面宽度B 值为263 mm［3］。

计算选用的车型为黄河JN150 重型货车，轮胎型号为11．0R20，轮胎尺寸为293 mm×1 085 mm，单轮

选择高等级沥青路面结构为研究对象，由上面层( 中粒式沥青混凝土) 、中面层( 粗粒式沥青混凝土) 、下面层( 沥青碎石) 、基层( 水泥稳定碎石) 、底基层( 二灰土) 和土基等6 个部分组成。选择用于高速公路的高等级沥青路面结构为研究对象，其相关计算参数参考文献［3］中路面结构各层的参数值，详见表1。

表1 计算用路面结构材料参数表

2 移动均布荷载在有限元模型中的实现

利用有限元软件ABAQUS 进行建模，计算过程中为了实现荷载的移动，首先沿荷载移动方向设荷载移动带，移动带沿路横向的宽度与施加的均布荷载宽度相同，沿路纵向的长度即为轮载行驶的距离［4-5］。然后，将荷载移动带细分成许多小矩形，如图1 所示，小矩形宽度根据计算精度而定，现取为加载宽度的1/3，每个矩形的大小为0．213 m×0．167 m，相当于标准圆形均布荷载作用于路面。依据垂直应力及接地尺寸的特性，路面模型的分析范围x 轴方向取为4 m，y 轴方向取为6 m，z方向取为6 m。计算采用8 结点等参元，边界条件假设为:底面上没有z 方向位移，左右面没有x 方向位移，前后面没有y 方向位移，层间完全连续。移动荷载沿纵向施加在路表面中心地带，如图1 所示。

图1 施加荷载移动带的路面模型

图2 移动带细分示意图

如图2 所示，初始状态汽车荷载占据三个小矩形的面积，即图2 中1、2 和3。汽车荷载沿移动带逐步向前移动，每个荷载步结束时，荷载整体向前移动一个小矩形面积，如第一个荷载步结束时，荷载占据面积即为2、3 和4。为了提高计算精度，每个荷步下面设多个荷载子步，如第一个荷载步中间荷载子步的作用使面积1 上的荷载逐渐减小，而面积4 上的荷载逐渐增大，依次变化达到荷载移动的效果。荷载的移动速度，可以通过设置每个荷载子步的时间大小来实现。

移动加载通过调用Fortran 语言编写的自编子程序来实现，随着时间的变化荷载沿预定义的路径向前移动，移动荷载的施加如图3 所示。移动荷载为大小0．7 MPa，为规范中规定的标准轮胎接地压强值［6］，设定的汽车移动速度选为25 m/s 也就是90 km/h，则0．24 s 前进6 m，按照网格尺寸的大小可知，汽车荷载在0．24 s 内占有36 个网格(6/0．167 =36) 。计算时采用8 结点等参单元，边界条件假设为:底面上没有y 方向位移，左右两侧没有x 方向位移，前后两侧没有y 方向位移，层间完全连续。施加移动荷载以后路面的变形图如图4 所示。

图3 移动荷载施加

3 正交模拟试验设计

正交试验设计是多因素分析设计的主要方法，是一种高效率、快速、经济的试验设计方法［7］。等水平的正交表可用如下符号表示: Ln( rm) ，其中，L 为正交表代号;n 为正交表横行数( 需要做的试验次数) ;r 为因素水平数;m 为正交纵列数( 最多能安排的因素个数) 。通过试验，可得到两个方面的结论: 第一，通过计算分析，可得出正交表中相对较好的方案; 第二，由于提出的方案并不可能涵盖所有的试验范围，所以利用正交表计算分析，分辨出主次因素，预测更好的参数组合，能为进一步试验提供有价值的依据。

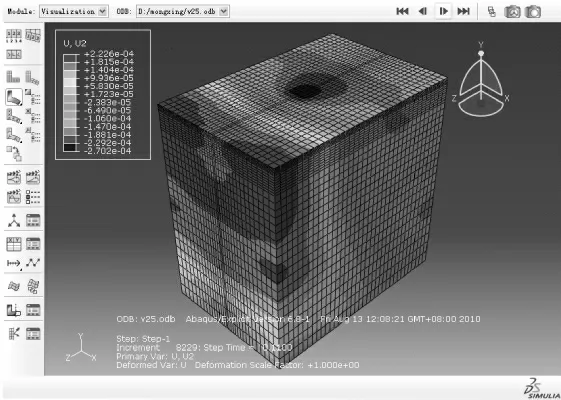
图4 移动荷载作用下t=0．1 s 时路面结构变形图

3．1 因素的选择

每个参数变化都会对路面的各响应有着不同的影响，所以为了更加全面地分析各参数变化以及不同参数进行组合时对路面各响应的影响，本正交试验的因素选取如表2 所示，包括上面层( 中粒式沥青混凝土) 、中面层( 粗粒式沥青混凝土) 、下面层( 沥青碎石) 、基层( 水泥稳定碎石) 、底基层( 二灰土) 的厚度，路面各层的弹性模量和各层泊松比，共17 个因素。

3．2 因素水平的确定

各因素水平的选择在公路设计规范［6］要求的范围内每一参数各选取三个变化值，如表2 所示。

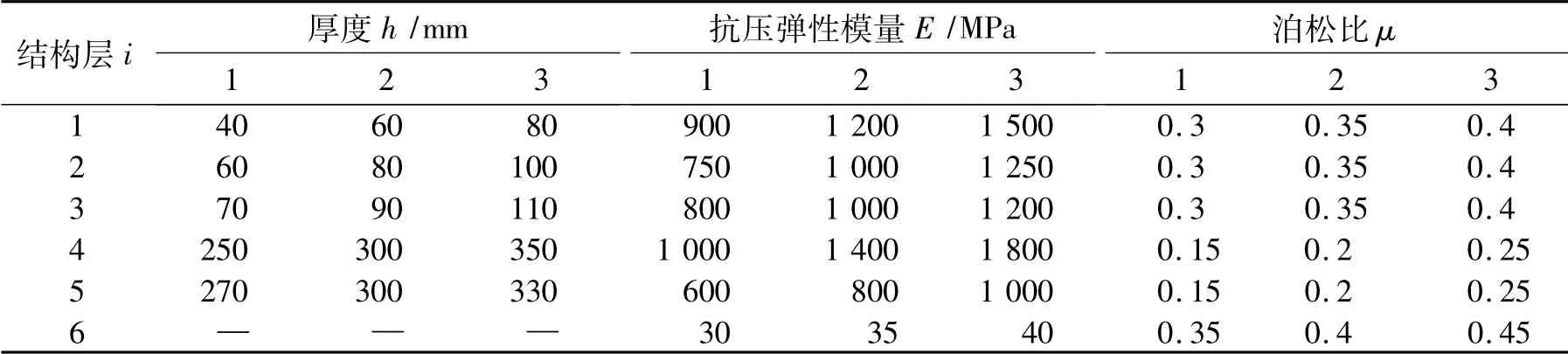
表2 路面结构各因素水平

注:表中第一列中的1、2、3、4、5、6 分别代表路面结构从上面层到土基的层次编号，第一行中的1、2、3 为各因素水平的编号。

3．3 考核指标的选择

由于路面各结构层的功能与受力性能不同，故结构层的材料参数变化必然对各结构层的力学响应产生影响。整个路面的最大弯沉以及最大水平剪应力均产生于上面层，最大竖向剪应力产生于基层，所以这几个响应都是需要考虑的因素;路面各层拉应力中纵向拉应力要大于横向拉应力，而两者的变化具有相似性，那么路面各层最大纵向拉应力也列入考查对象，同时还需要考虑国际上提出的设计指标:沥青层底部的水平拉应变，它产生疲劳开裂;另一个是土基表面的竖向压应变，它是整个路面竖向拉应变的最大值;且经过计算，路面最大水平拉应变产生于底基层，因此这一响应也列入考虑范围。所以，最终考核指标的选择为上面层最大弯沉、上面层最大水平剪应力、基层最大竖向剪应力、各层最大纵向拉应力、下面层底部的水平拉应变、产生于底基层的最大水平拉应变以及土基表面的竖向压应变，共12 个指标。

3．4 正交表的选择

数值模拟试验为17 因素3 水平的正交实验，如果进行全面试验需要进行317 次实验，工作量是巨大的，所以选用正交试验方法可以大大降低工作量。而正交表的选择则可以利用统计分析软件SPSS［8］来生成，经SPSS 的分析本正交试验需要L64(317) 的正交表，也就是需要进行64 次数值模拟试验。

4 沥青路面结构优化设计方案选择

4．1 正交数值模拟试验结果

因为是多指标试验，所以选择的计算结果分析方案为多指标直观分析。各因素对于上面层最大弯沉的影响如表3 所示( 由于篇幅所限，各因素对于上面层最大水平剪应力、基层最大竖向剪应力、路面各层最大纵向拉应力、下面层底部的水平拉应变、产生于底基层的最大水平拉应变以及土基表面的竖向压应变等考核指标的影响文中未列出) 。

4．2 沥青路面结构优化方案选择

表3 中列出的计算结果为各因素对于上面层最大弯沉的影响，根据极差由大到小的排列可以看出对于上面层最大弯沉值这一考核指标各因素的影响由大到小分别为μ6、h3、E6、E4、h4、E5、μ2、h5、μ1、E1、E2、h1、μ5、h2、μ3、E3、μ4，又由每一个因素水平使上面层最大弯沉值的均值达到最小来进行选取( 如表3 中上面层h1这一参数的选取，均值k1、k2、k3分别为-0．378 3、-0．374 0、-0．398 6，其中最小值为k2，所以h1选取因素水平2，也就是表2 中的h12为60 mm) ，所以根据上面层最大弯沉值这一考核指标所选取的各参数为h12、h23、h33、h43、h53、E12、E23、E32、E43、E52、E63、μ12、μ22、μ32、μ42、μ51、μ63。同理可以根据其他考核指标中各因素对于路面各层的影响，得出表4。

表3 各因素对于上面层最大弯沉的影响

注: kj( j = 1，2，3) 表示任一列上因素取水平j 时所得实验结果的算术平均值;R 为极差，为某一因素时3 种水平下考核指标均值之差的绝对值的大小，反映了该因素对试验结果影响的大小。

表4 基于各考核指标的影响因素主次及各层因素水平的选取

根据表4 的分析计算结果可知:(1) 对于上表面最大弯沉影响最大的因素是土基泊松比μ6;(2) 对于上面层最大水平剪应力影响最大的因素是基层模量E4;(3) 对于基层的最大竖向剪应力影响最大的因素是基层厚度h4;(4) 对于上面层最大纵向拉应力影响最大的因素是上面层厚度h1;(5) 对于中面层最大纵向拉应力影响最大的因素是上面层厚度h1;(6) 对于下面层最大纵向拉应力影响最大的因素是基层模量E4;(7) 对于基层最大纵向拉应力影响最大的因素是基层模量E4;(8) 对于底基层最大纵向拉应力影响最大的因素是底基层模量E5;(9) 对于土基最大纵向拉应力影响最大的因素是土基泊松比μ6;(10) 对于下面层底部的水平拉应变影响最大的因素是基层模量E4; (11) 对于底基层的最大水平拉应变影响最大的因素是底基层模量E5;(12) 对于土基表面的竖向压应变影响最大的因素是土基层泊松比μ6。

在表4 中所分析的12 个考核因素中，基层弹性模量E4的变化对于各考核指标的影响最大，并且在对各考核指标影响因素的主次方面比较靠前;其次是土基泊松比μ6与上面层厚度h1，都是影响各考核指标最大的几项因素。从模拟试验结果中可以看出，基层弹性模量E5的提高可以有效地减小上面层最大弯沉，而且对比面层弹性模量的增加会有比较好的经济效益。在经过正交试验分析后可以发现对于上面层最大弯沉影响最大的则是土基的泊松比μ6变化，同时泊松比μ6变化对于土基的最大拉应力影响是最大的，所以从这点看来，不能忽视土基泊松比μ6变化对于路面响应所带来的影响。面层厚度的变化中，上面层厚度h1的变化，它是影响路面上中面层最大拉应力的主要因素，而且对于上面层来说增加其厚度有利有弊，随着上面层厚度的增大，上面层最大弯沉减小，但并非越大越好。从经济角度考虑，上面层加厚会增加整体建设造价，而且由于上面层直接暴露于空气之中，过厚的沥青表面层的高温稳定性也会比较差，更容易出现车辙。

由于一共有12 个考核指标，所以最终得到12 组路面参数组合，如表4 所示。比较选择这12 组参数组合中各因素水平应用次数最多的一项作为这一层的最佳参数值( 如参数h1的选择:因素水平2 在12 组路面参数组合中一共用到了5 次，因素水平1 一共用到了3 次，因素水平3 一共用到了4 次，所以上面层厚度的选择为因素水平2，即h12) ，所以可以得到路面各层参数的最佳组合为:h12(60 mm) 、h23(100 mm) 、

h32(90 mm) 、h43(350 mm) 、h53(330 mm) 、E11(900 MPa) 、E23(1 250 MPa) 、E33(1 200 MPa) 、E43(1 800 MPa) 、E53(1 000 MPa) 、E61(30 MPa) 、μ13(0．4) 、μ22(0．35) 、μ31(0．3) 、μ43(0．25) 、μ51(0．15) 、μ61(0．35) 。

再根据此组参数建立路面模型，最终对应路面各结构层的动力响应最大值分别为: 上面层最大弯沉为-0．535 3 mm，上面层最大水平剪应力为0．0134 2 MPa，基层最大竖直剪应力为0．068 18 MPa，上面层最大拉应力为0．096 48 MPa，中面层最大拉应力为0．069 68 MPa，下面层最大拉应力为0．051 73 MPa，基层最大拉应力为0．045 08 MPa，底基层最大拉应力为0．061 56 MPa，土基最大拉应力为0．001 929 MPa，下面层底水平拉应变为12．002 ×10-6，底基层底水平拉应变为12．002 ×10-6，土基层顶面竖直压应变为-185．6 ×10-6。分析可知，与所有的正交试验得到的响应最大值相比，该路面结构各响应最大值总体是最小的。因此，分析得到的最佳路面参数组合可以作为以重型卡车行驶为主且速度较高情况时一个较好的设计方案。

5 结论

利用有限元软件ABAQUS 建立路面模型，调用Fortran 语言编写的自编子程序实现路面移动荷载的施加。应用正交试验方法对路面参数进行优化具有明显的优越性，不仅可以考虑多个因素和不同的因素水平，而且可以考虑多个考核指标。在因素与因素水平较多时，可以利用统计分析软件SPSS 生成正交表。选取17 个因素、3 因素水平、12 个考核指标综合分析所得出的优化设计方案可以认为是沥青路面结构最佳参数组合，其对应的路面各结构层动力响应总体上是最小的，即整个路面的破坏程度最小。文中沥青路面结构设计主要是针对重型卡车以较高速度行驶时的情况，分析方法和思路可供其它情况借鉴。

［1］邓学钧，黄晓明．路面设计原理与方法［M］．北京:人民交通出版社，2001．

［2］许迪，许志鸿，张东升．基于正交理论的长寿命沥青路面力学指标分析［J］．上海大学学报，2008，12(12) :623-628．

［3］孙立军．沥青路面结构行为理论［M］．上海:同济大学出版社，2003．

［4］庄茁，张帆．ABAQUS 非线性有限元分析与实例［M］．北京:科学出版社，2005．

［5］廖公云，黄晓明．ABAQUS 有限元软件在道路工程中的应用［M］．南京:东南大学出版社，2008．

［6］中交公路规划设计院．JTG D50—2006 公路沥青路面设计规范［S］．北京:人民交通出版社，2006．

［7］方开泰，马长兴．正交与均匀实验设计［M］．北京:科学出版社，2001．

［8］徐向宏，何明珠．试验设计与Design-Expert、SPSS 应用［M］．北京:科学出版社，2010．