曲曲连接新型缓和曲线线形动力特性分析

2011-02-15杨庆花李向国闫公甫

石家庄铁道大学学报(自然科学版) 2011年3期

杨庆花，李向国，周泉，闫公甫

(1．中铁上海设计集团有限公司天津分院，天津 300073;2．西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031;3．石家庄铁道大学土木工程学院，河北石家庄 050043;4．天津滨海快速交通发展有限公司，天津 300451)

随着列车行车速度的不断提高，高速铁路运行的安全性和舒适性对轨道的平顺性、稳定性提出的更高的要求。而我国总的铁路运营里程中，有近三分之一的线路是曲线［1］。因此在保证高速行车安全和旅客乘坐舒适度要求下，如何因地制宜，减少工程投资将曲线与曲线进行合理的连接，成为了摆在我们面前的又一课题。首先基于工况困难条件下，取消夹直线长度，提出连接两圆曲线的新型缓和曲线( 圆圆型缓和曲线) ，然后选取车体横向加速度及其时变率、车体侧滚角速度及其角加速度舒适度指标，对高速铁路上曲曲连接使用的“圆曲线—缓和曲线—夹直线—缓和曲线—圆曲线”形式的三次抛物线缓和曲线与本文提出的“圆曲线—缓和曲线—圆曲线”形式的新型缓和曲线进行力学性能对比分析。

1 新型缓和曲线方程

取工况困难条件下，圆曲线与圆曲线直接由缓和曲线连接，即夹直线长度为零，缓和曲线根据缓和曲线曲率边界条件，列出缓和曲线曲率微分方程式，进而求其通解，即为缓和曲线曲率方程通式。

作为特例，假定连接圆曲线与圆曲线的缓和曲线满足边界条件: YH 点( 起点l = 0 ) 处，y = 0，φ = 0，k = 1/R，k′ = 0 ; HY 点( 终点l = l0) 处，k = 1/R，k′ = 0 ;在l = lm处曲率为最小值klm= 0，klm′ = 0 。用通用方法推导其方程的过程如下。

首先，曲率边界条件有6 个，即

则曲率待定方程为

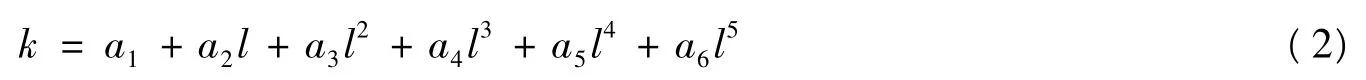
然后，将曲率边界条件式(1) 带入曲率待定方程式(2) ，并令lm= 0．5l0，可解得待定系数a1= 1/R，a2=0，a3=，即曲率方程为

最后，对曲率方程式(3) 进行一次积分得缓和曲线偏角方程

式中，积分常数C1由边界条件起点处偏角φ = 0 可确定出C1= 0 。

再对缓和曲线偏角式(4) 进行一次积分得缓和曲线方程

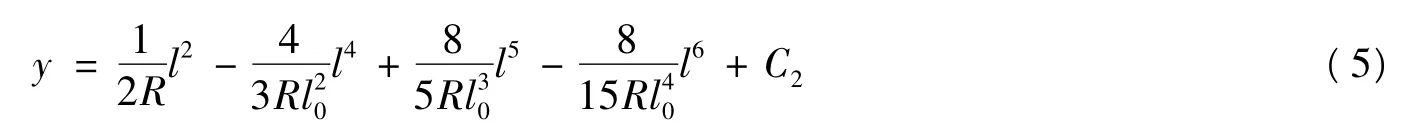
式中，积分常数C2由边界条件起点处纵坐标y = 0 可确定出C2= 0 ，从而得到缓和曲线方程

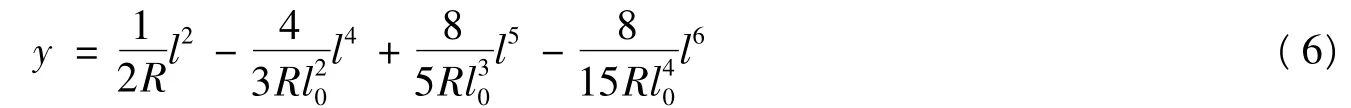
2 列车高速通过曲曲连接理论分析

2．1 列车高速通过曲曲连接舒适性评价指标

“铁路旅客舒适度”指的是旅客在列车上感觉到的舒适程度。广义上讲旅客舒适度是乘坐铁道车辆旅行的人对乘车旅行品质的综合反应评价。狭义来说，旅客舒适度是列车运行产生的振动( 加速度) 对乘客的影响问题［2］。主要研究高速列车通过曲线时的动力特性，因此采用以下评价指标来评价高速列车通过曲曲连接线路时旅客的舒适性。

2．1．1 车体横向加速度［3］an

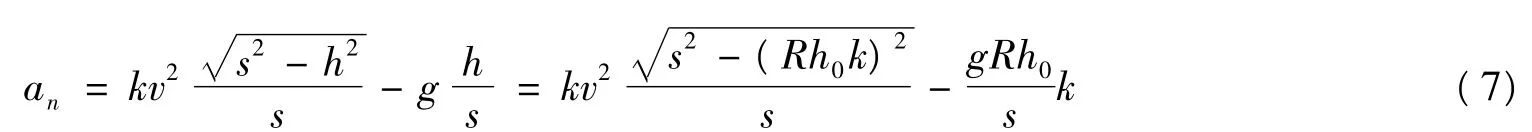
2．1．2 车体横向加速度时变率［3］f

未考虑速度变化时的横向加速度时变率

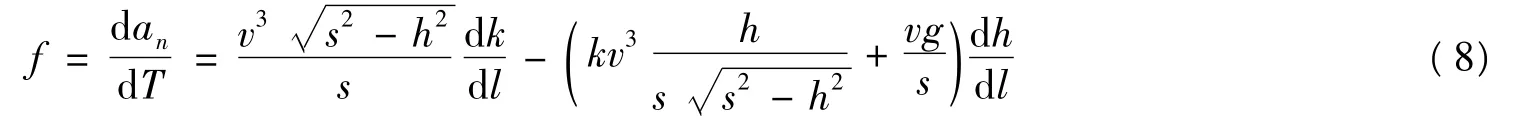
考虑速度变化时的横向加速度时变率

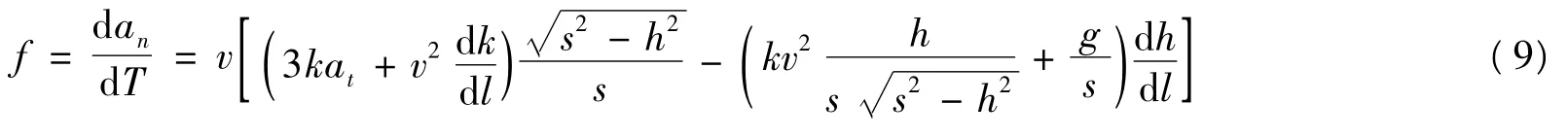
2．1．3 车体侧滚角速度ω

以车体纵向中心线为轴线的转动角称为侧滚角，其随时间的变化率称之为侧滚角速度。在直线行驶时，侧滚角速度可以忽略。但当列车在缓和曲线上运行时，侧滚角速度正比于曲线超高的变化率，并会引起车体的侧滚运动。列车速度越高，侧滚角速度也越大，当超过某一值时就会影响乘客的舒适度。由于超高角很小，故车轴与水平面倾角φ 为［4］

则式(10) 两边对时间T 求导得侧滚角速度为

2．1．4 车体侧滚角加速度β

当列车运行速度变化时，将式(11) 两边对时间T 求导即可得到车体侧滚角加速度

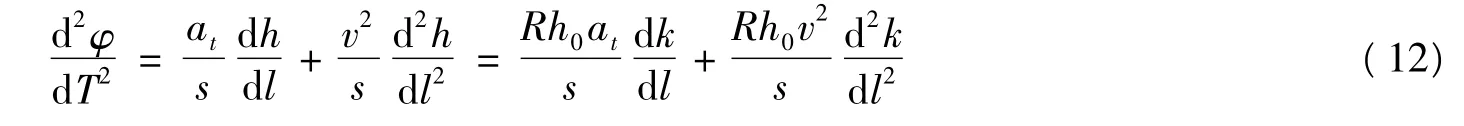
若列车运行速度恒定，即at= 0，则车体侧滚角加速度为

2．2 计算内容及参数

计算内容:从运动学角度出发，利用Matlab 编程进行数值计算，建立以下三种工况:列车在整个曲线上以速度300 km/h 恒速行驶( 工况1) ;当列车以纵向加速度at= 0．33 m/s2，从初速度v0= 300 km/h 开始匀加速通过整个曲线( 工况2) ;当列车以纵向加速度at= -0．47 m/s2，从初速度v0= 300 km/h 开始匀减速通过整个曲线( 工况3) 。计算参数为:线路为平坡，缓和曲线长度为l = 485 m，圆曲线半径为R =5 000 m，外轨最大超高为h = 160 mm;夹直线长0．8v0= 240 m。新型缓和曲线与三次抛物线缓和曲线的超高简图如图1 所示。

图1 缓和曲线超高

2．3 计算结果及对比分析

计算结果如图2 ～图7 所示，理论分析结果如表1。

图2 车体横向加速度(匀速)

图3 车体横向加速度时变率(匀速)

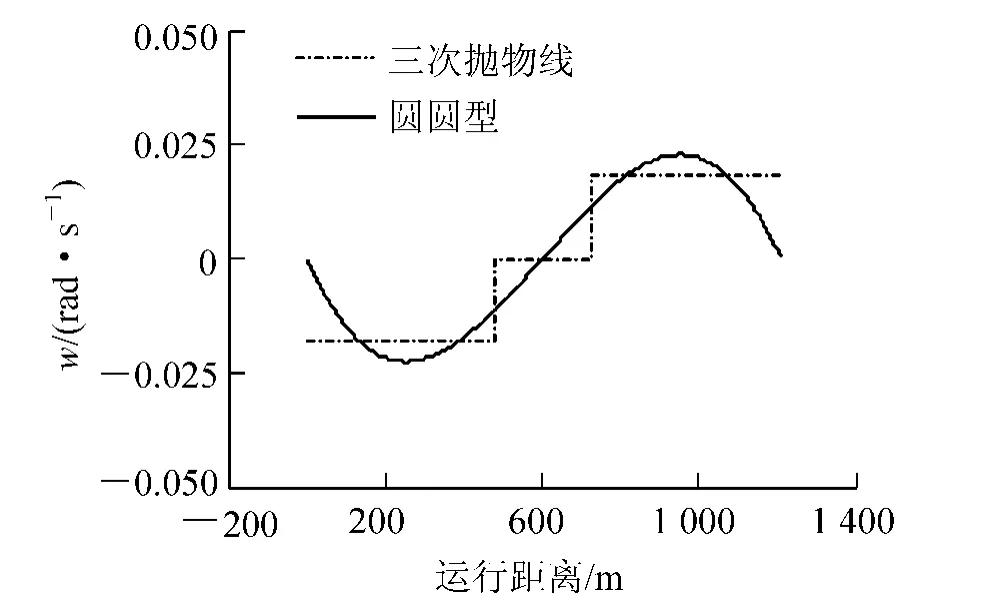
图4 车体角速度(匀速)

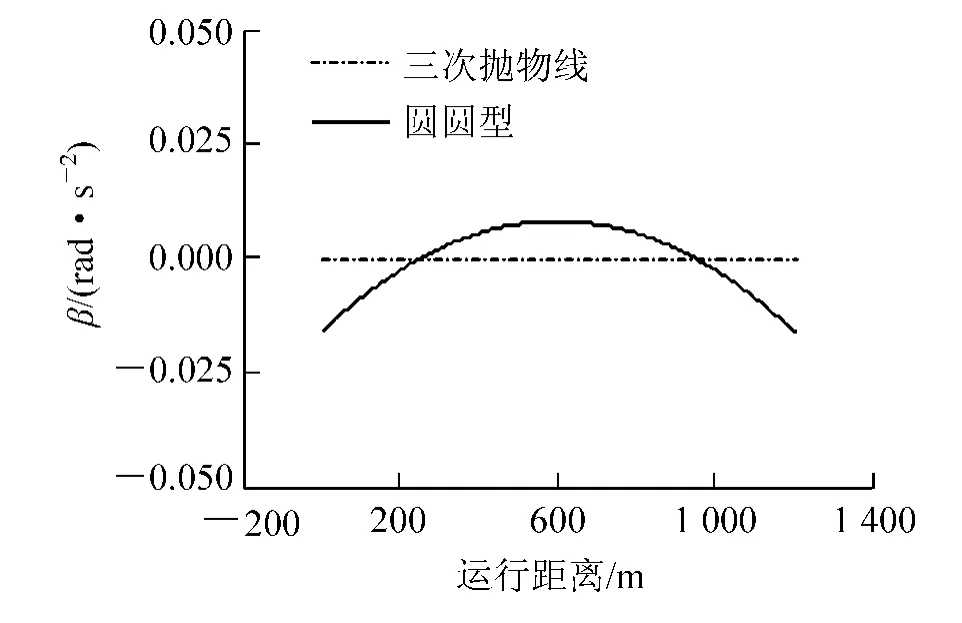
图5 车体角加速度(匀速)

(1) 从图2、图3 及表1 可以看出，对于车体横向加速度时变率及车体侧滚角速度，当列车以300 km/h恒速通过整个曲线，三次抛物线在曲线上的4 个连接点( 直缓点、缓圆点、圆缓点、缓直点) 处均有突变，而新型缓和曲线圆圆型没有突变，且二者的横向加速度时变率及车体侧滚角速度最大值较接近。

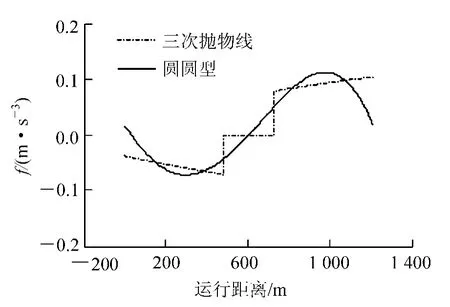
图6 车体横向加速度时变率(匀加速)

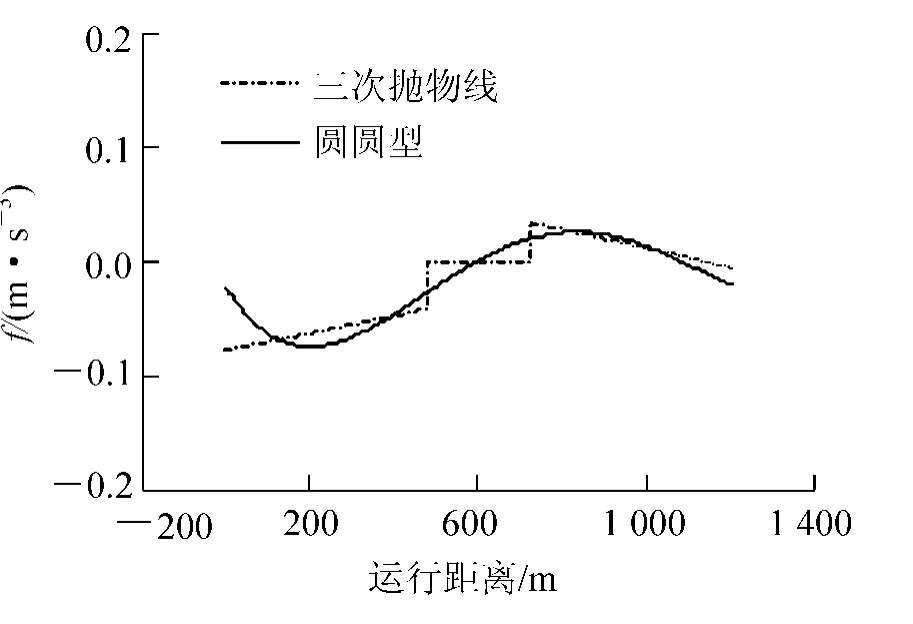
图7 车体横向加速度时变率(匀减速)

(2) 在工况2 下，三次抛物线在四个连接点的车体横向加速度时变率及车体侧滚角速度突变值较大，说明随着速度的提高旅客乘坐舒适性降低;在三种工况下，由于圆圆型缓和曲线只有车体侧滚角加速度在起终点有较小突变值，对于其他三个舒适性指标在整个曲线上都变化均匀，说明圆圆型缓和曲线以不同速度高速通过曲线时的旅客乘坐舒适性较好。

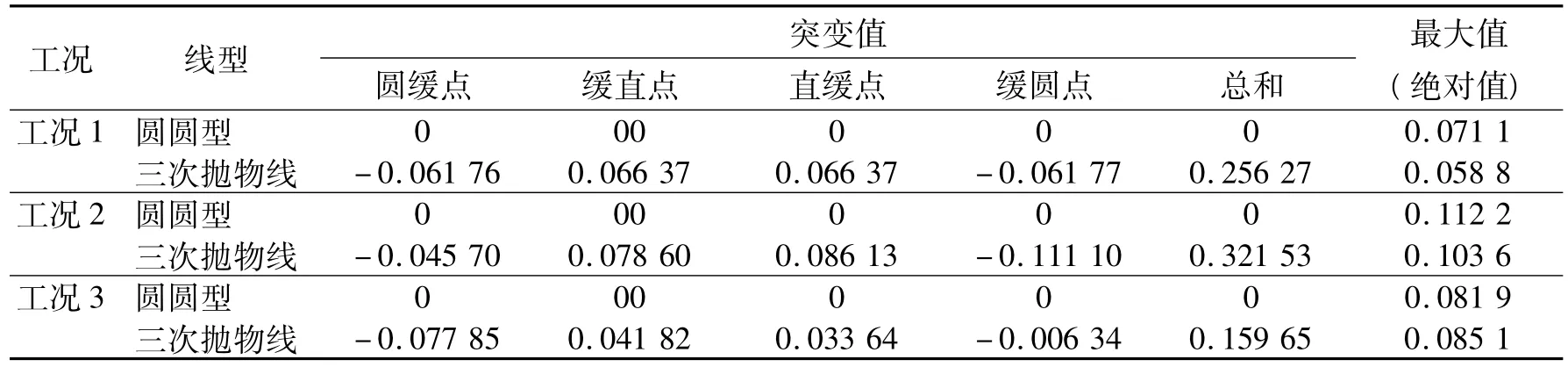
表1 高速行车车体横向加速度时变率突变值与最大值对比

3 列车高速通过曲曲连接的动力特性分析

3．1 仿真软件及模型

(1) 仿真软件。仿真软件采用目前俄罗斯最为通用的机械动力学/运动学仿真分析软件Universal Mechanism( 简称UM) 软件。该软件由俄罗斯布良斯克国立理工大学( Bryansk State Technical University)Dmitry Pogorelov 教授研发，具有高效易用的前后处理功能并支持并行计算技术，模型修改方便、计算速度较快。

(2) 车辆模型。车辆系统是一个复杂的多自由度、非线性多刚体系统，其本身包括许多非线性因素，如非线性轮轨相互作用关系、非线性弹簧阻尼悬挂特性等。在车辆动力学中，建立用于研究机车车辆的数学模型时，系统中除弹性、阻尼元件外的各个部件，如车体、构架、轮对等都视为刚体。一个刚体有6 个自由度，分别沿3 个坐标轴的线位移和绕3 个坐标轴的转动位移分别对应伸缩、横移、沉浮、摇头、侧滚、点头等6 中基本振动形式，仿真车辆采用单节车辆。

(3) 轨道模型。本文研究的动力特性分析主要针对线路特殊线型条件下对车辆动力响应的影响，因此着重分析线路参数对车辆动力响应的影响。轨道模型采用UM 软件建模，钢轨作为弹性连续梁处理，梁与下部基础在垂向上考虑为并联线性弹簧/阻尼联结、横向上考虑为串联线性弹簧/阻尼联结。采用的钢轨为中国60 kg/m 标准断面新轨;其线路无砟轨道模型的力学模型简图见图8。

3．2 仿真计算参数及仿真结果

仿真线路参数及内容如2．2 所示，列车高速通过各曲线线形的部分舒适性指标如图9 ～图14 所示。

3．3 仿真结果及理论结果对比分析

(1) 由仿真结果图9，图10 与理论结果图2，图3 可以看出，两缓和曲线的横向加速度在整个曲线上的变化趋势基本一致。只是三次抛物线在四个连接点( 直缓点、缓圆点、圆缓点、缓直点) 处有较大激扰，而圆圆型缓和曲线只在两个连接点( 直缓点、缓直点) 有较小激扰，它们的最大值几乎一样，因此圆圆型缓和曲线的乘坐舒适性较好。

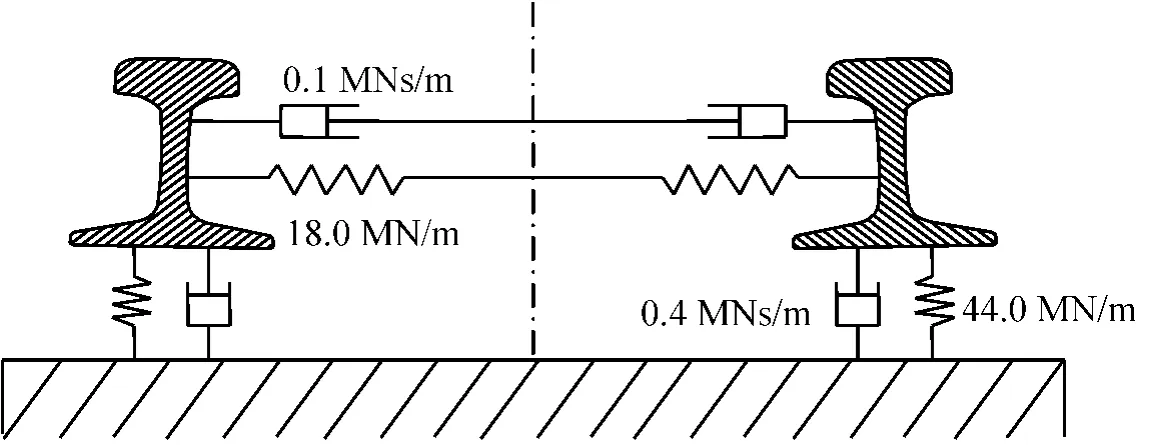
图8 轨道力学模型

图9 车体横向加速度(匀速)

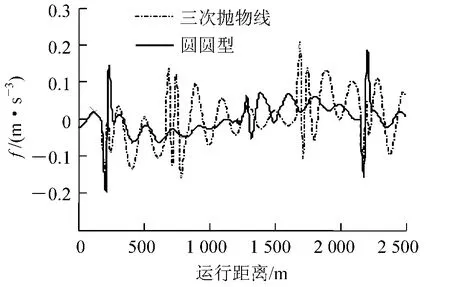
图10 车体横向加速度时变率(匀速)

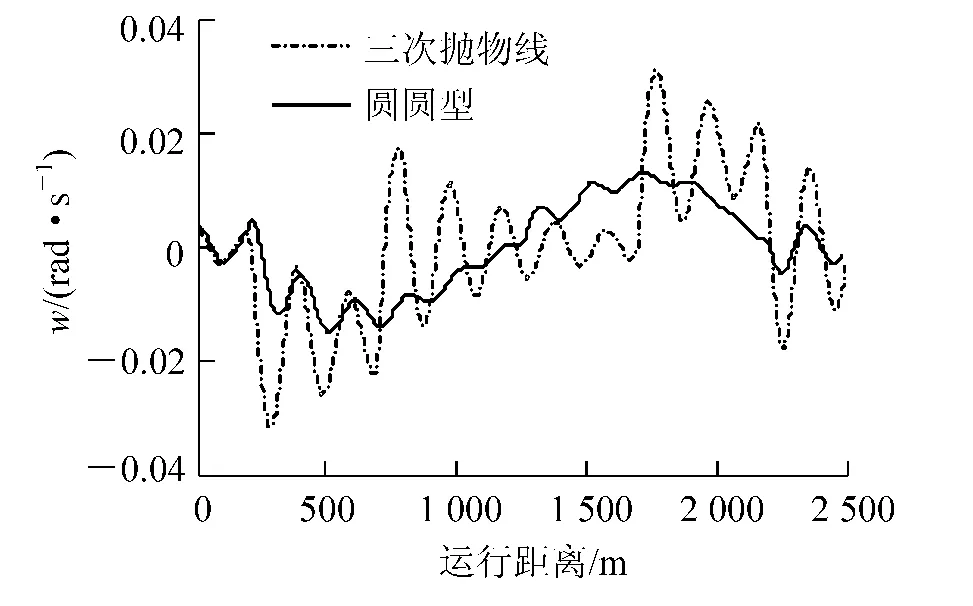
图11 车体角速度(匀速)

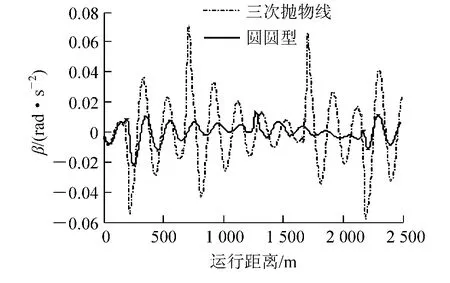
图12 车体角加速度(匀速)

图13 车体横向加速度时变率(匀加速)

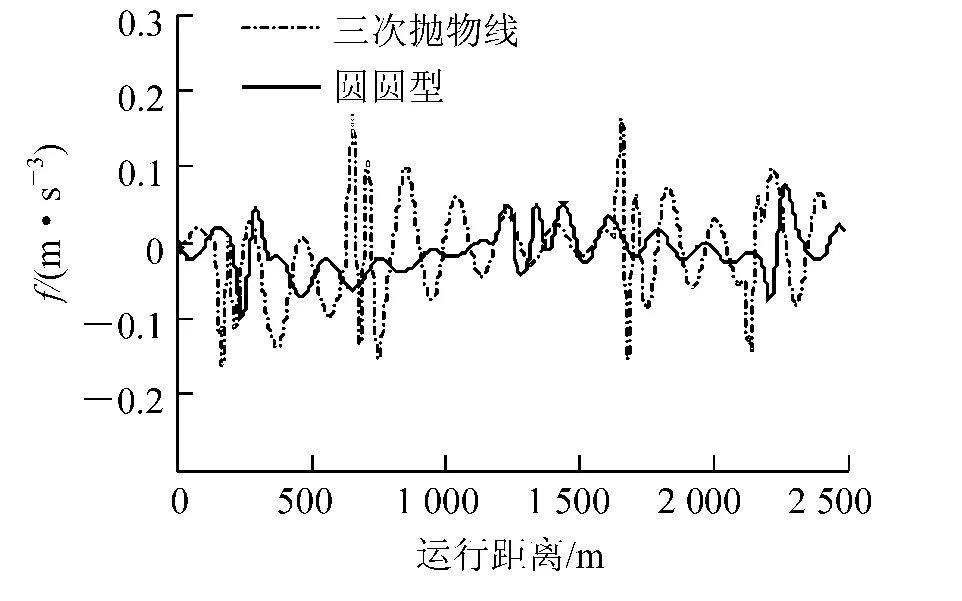
图14 车体横向加速度时变率(匀减速)

(2) 对于车体横向加速度时变率，与横向加速度的变化情况基本一致。两缓和曲线仿真结果与理论结果变化趋势较接近。仿真结果中在工况1 下，圆圆型缓和曲线在起终点的激扰较大，但是在工况2、3下，圆圆型缓和曲线横向加速度时变率在整个曲线上比三次抛物线小，而且三次抛物线在四个连接点处有激扰，说明三次抛物线的四个连接点处，旅客乘坐舒适性较差，圆圆型缓和曲线乘坐舒适性较好。