海洋细长结构参数激励不稳定区的确定方法
2011-02-13徐万海吴应湘钟兴福刘培林冯现洪
徐万海,吴应湘,钟兴福,何 杨,刘培林,冯现洪
(1.天津大学 建筑工程学院,天津 300072;2.中国科学院 力学研究所,北京 100190;3.海洋工程股份有限公司,天津 300451)
21世纪是海洋经济时代,随着世界经济的快速发展,能源短缺问题日益突出,由于陆上及近海的石油资源日益枯竭,深海油气开发已成为各国能源战略的重点。根据不同的海洋环境及经济方面的考虑,会采取不同的平台开采方案,如张力腿平台(TLP),SPAR平台,半潜平台等。不论海洋油气开发采用何种平台方案,张紧式细长柔性结构如立管、张力腿等都会在其中扮演重要的角色。立管是进行深水油气开采必不可少的设备,它连接海底矿藏与海面的作业平台,进行钻探、导液和泥浆等工作。张力腿一般为圆柱形结构,是连接张力腿平台与海底锚固基础的关键部件,提供平台本体必要的结构刚度。立管与张力腿结构形式有很大的相似之处,最大的不同就是立管的轴向预张力比张力腿小,同时立管内部有流体流动[1],如果忽略内流影响,两种结构的动力响应分析方法是一致的。
张力腿等细长的海洋工程结构,主要受到两种外部激励形式的作用,一种是平台纵荡而产生的受迫振动,第二种是平台垂荡引起的参数振动[2,3]。前人的研究工作主要集中在两方面:一种是将张力腿简化为线性Euler-Bernoulli梁模型,同时考虑平台纵荡和垂荡激励作用[2,3];另一种是把张力腿看成非线性梁结构,为了简单起见,仅考虑平台的垂荡激励[4,5]。上述的两种简化方法,最终得到张力腿参数振动的控制方程均为Mathieu方程。当采用非线性梁模型,同时考虑平台垂荡与纵荡共同作用,研究张力腿的非线性动力响应还很少见。综合地考虑轴向与流向的非线性因素及耦合效应时,张力腿参数振动的控制方程不再是Mathieu方程,而变为更一般的 Hill方程[6]。
本文的主要目的是给出不同情况下,Hill方程不稳定区的确定方法,同时比较不同方法之间的不同之处,并给出各自的适用范围。
1 控制方程
张力腿被简化为两端简支的梁结构,假设顶端平台的运动是关于时间的简谐函数,采用Han和Benaroya[7]提出的非线性模型,忽略转动惯量和扭转效应的影响,应用Galerkin法和模态展开原则,得到描述张力腿等细长的海洋工程结构参数激励系统的无量纲Hill方程[6]:
Ua,Va分别为平台垂荡和纵荡的幅值,L为张力腿的长度。
2 Hill方程的不稳定区域确定方法
Hill方程的解会根据不同的δ,ε和M组合而变得稳定或者不稳定。由于水动力阻尼的存在,张力腿等一般不会发生参数失稳。但在不稳定区内,张力腿的动力响应幅值明显大于稳定区域内的结果,所以确定Hill方程不稳定区域是十分必要的。关于不稳定区的分析有很多种方法,其中摄动方法和傅里叶分析是比较常用的。
2.1 变形参数法[8]
令:

将式(4)代入Hill方程式(1),根据ε的阶次整理:
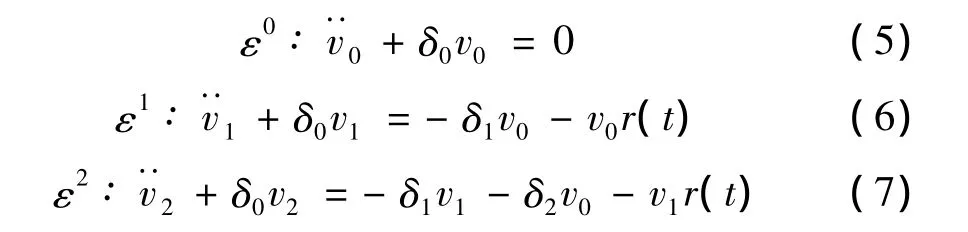
方程(5)的解必须是周期为π或2π的周期函数:

因此:

由于变形参数法确定Hill方程不稳定区时,随着n数值的增加计算量会变得相当可观。在此只讨论n=0,1,2 的情况。
(1)n=0时
δ0=0,有v0=a,于是:

v1必须是周期的,因此δ1=0,化简求解式(10),并将v1代入式(7)中:

其中NST为长期项,消去长期项,得到边界曲线为:
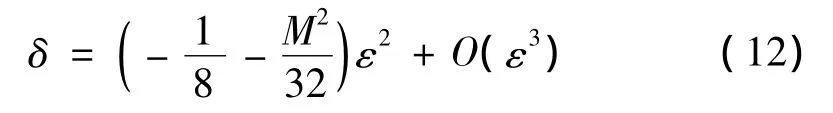
(2)n=1时
当n≠0时,方程(5)的通解为:

把式(13)代入式(6):

当n=1时,消去式(14)中的长期项:



消去式(17)中的长期项,边界曲线为:


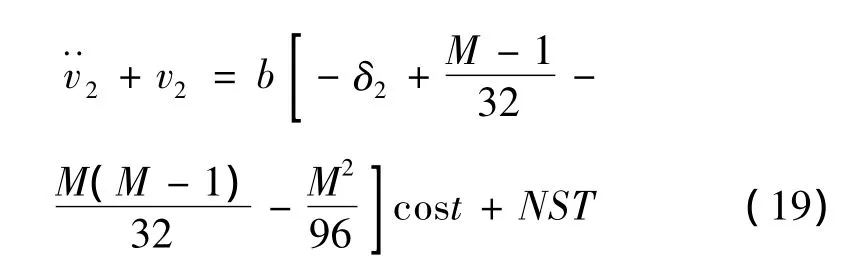
消去式(19)的长期项,边界曲线为:

(3)n=2时
当n=2时,消去式(14)中的长期项:


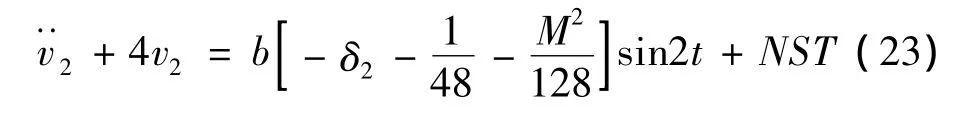
消去式(23)中的长期项,边界曲线为:



消去式(25)中的长期项,边界曲线为:

2.2 改进的变形参数法
应用变形参数法进行稳定区域的理论分析时,必须满足ε≪1,很多情况下,ε≪1的假设并不满足,所以传统的变形参数法已经不再适用。很多学者对该方法进行了改进[9,10],改进的变形参数法可以用来确定参数激励的幅值不是很小的Hill方程不稳定区。
设δ是ε的多项式函数,即:

式中:δ0,ω1,ω'2,ω'3,…均为任意常数。由于 ε 可以不是小量,引入一个新的小参数:


于是式(27)可以写成:

式中:δ0,ω1,ω2,ω3,…均为任意常数。
令:

把ε,δ,v的表达式代入式(1)中,比较α的同次幂项系数:

运用变形参数法确定参数振动不稳定区相同的公式推导方法,最终得到相应的边界曲线表达式:
(1)n=0时
边界曲线为:
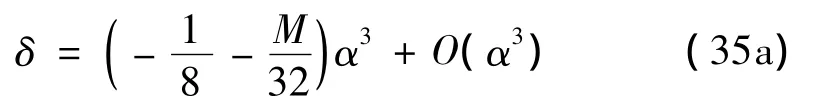

(2)n=1时
为消除方程中的长期项,需满足如下关系式:


边界曲线为:
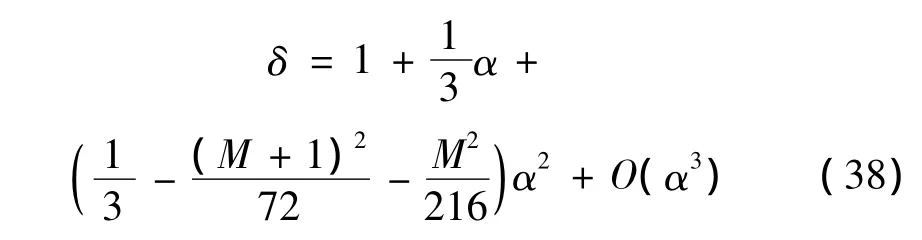
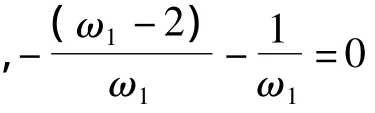
边界曲线为:

(3)n=2时
为消除方程中的长期项,需满足如下关系式:


边界曲线为:

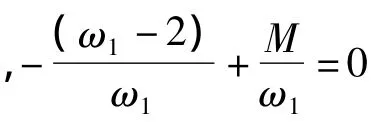
边界曲线为:

2.3 傅里叶分析法
当δ和ε是小参数时,Hill方程的不稳定区域根据摄动方法可以获得,但是实际的海洋环境条件下,δ和ε不再是小参数,变形参数方法不再适用,而改进的变形参数方法仅仅能分析ε~1的情况,大参数情况下同样不适用。所以需要采用傅里叶分析法来确定Hill方程不稳定区域。
当δ是方程(1)的可列特征值时,下面的周期解满足式(1)[11]



把方程(44)、(45)、(46)和(47)代入式(1),相应的cos(2nτ),cos(2n+1)τ,sin(2nτ)和 sin(2n+1)τ 各项前面系数等于0,经过整理,得到无穷项的行列式关系如下:

可以根据实际工程设计需要,截取有限项n,应用简单的数值方法可以得到Hill方程的不稳定区图像。
3 Hill方程的不稳定区图像
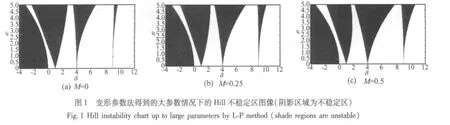
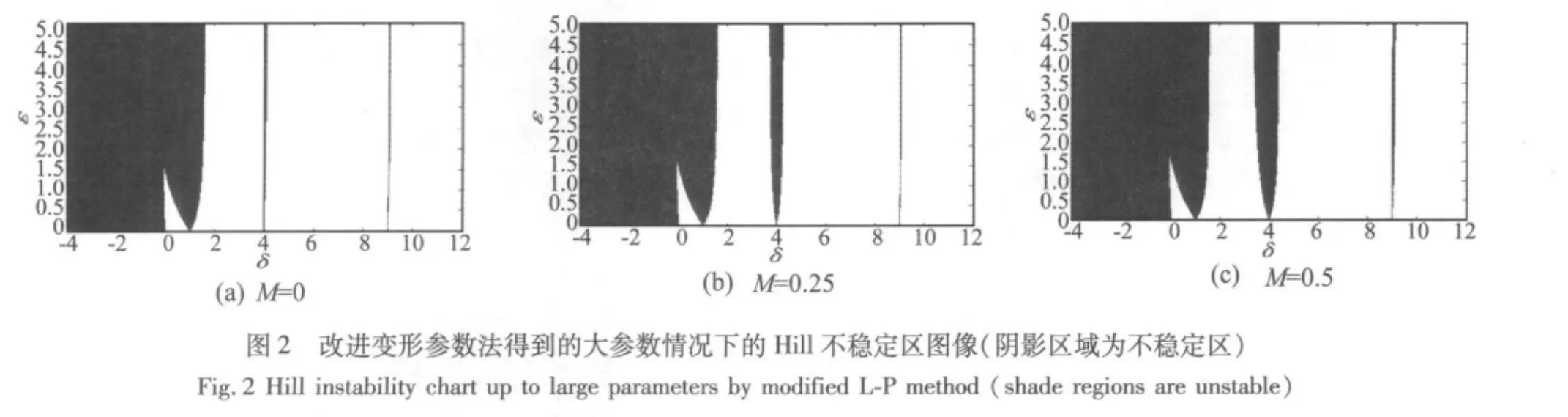
应用MATLAB软件画出变形参数法以及改进的变形参数法得到的Hill方程不稳定区,分别取M=0,M=0.25,M=0.5,图1和图2分别给出了用上述两种摄动方法得到的Hill方程的前3阶不稳定区。
然后给出傅里叶分析方法获得的不稳定区。为了简化计算过程,同时保证最终结果的正确性和足够的精度,截取式(48)~式(51)中的有限10项,分别取M=0,M=0.25,M=0.5,应用 MATLAB 软件编程,画出大参数情况下方程(1)的不稳定图,δ和ε的取值范围限定在0到20,图3给出了Hill方程(1)的前3阶不稳定区。对比图1、图2和图3可以发现,大参数情况下,Hill方程(1)的不稳定区相比于小参数情形,具有明显的不同。

4 结论
本文给出了三种不同的确定Hill方程不稳定区方法、分别为变形参数法、改进变形参数法及傅里叶分析法,通过对三种方法优缺点的对比,可以得到如下结论:
(1)参数激励系统的控制方程是小参数的Hill方程时,可以采用变形参数法、改进变形参数法分析其不稳定特性,分析结果具有较高的精度。但计算量会随着不稳定区阶数的提高,变得十分巨大。
(2)参数激励系统的控制方程不是小参数的Hill方程时,需要采用傅里叶分析法讨论其解的不稳定性,实际计算表明,傅里叶分析法可以根据需求得到高阶不稳定区,并且其思路简单,计算量不大,建议在张力腿、立管等细长海洋结构的设计计算过程中采用。
[1]Moe G,Stromsem K C,Fylling I.Behaviour of risers with internal flow undervarious boundary conditions[C].Proceedings of the Fourth International Offshore and Polar Engineering Conference,1994,2:258-262.
[2] Patel M H,Park H I.Combined axial and lateral responses of tensioned buoyant platform tethers[J]. Engineering Structure,1995,17:687-695.
[3]Park H I,Jung D H.A finite element method for dynamic analysis of long slender marine structures under combined parametric and forcing excitations[J].Ocean Engineering,2002,29:1313-1325.
[4]Chatjigeorgiou I K.On the parametric excitation of vertical elastic slender structures and the effect of damping in marine applications[J].Applied Ocean Research,2004,26:23-33.
[5]Chatjigeorgiou I K,Mavrakos S A.Nonlinear resonances of parametrically excited risers numerical and analytic investigation for Ω =2ω1[J].Computers and Structures,2005,83:560-573.
[6]Xu W H,Zeng X H,Wu Y X.Hill instability analysis of TLP tether subjected to combined platform surge and heave motions[J].China Ocean Engineering,2008,22(4):533-546.
[7]Han S M,Benaroya H.Nonlinear coupled transverse and axial vibration of a compliant structure 1:formulation and free vibration[J]. Journal of Sound and Vibration,2000,237(5):837-873.
[8]Nayfeh A H.Introduction to Perturbation Technique[M].New York:Wiley,1981.
[9]袁镒吾,张 伟.参数激励的幅值不是很小时Mathieu方程的一种解法[J].应用力学报,2000,17(3),128-132.
[10]张海燕,唐友刚,谢文会,用改进的变形参数法求解强参数激励Mathieu方程[J].天津大学学报,2006,39(11),1289-1292.
[11] Patel M H,Park H I.Dynamics of tension leg platform tethers at low tension-part 1:Mathieu stability at large parameters[J].Marine Structures,1991,4:257-273.
