阿克苏流域可能蒸发量的计算

霍 文，杨 青，李 杨，秦 贺

（1.中国气象局 乌鲁木齐沙漠气象研究所，乌鲁木齐 830002；2.新疆维吾尔自治区气象台，乌鲁木齐 830002）

蒸发是生态系统水分循环与水量平衡的重要组成部分，直接关系着地表能量平衡和水量平衡［1］。气候变化影响水循环的各个环节，除通过降水和气温变化影响流域径流的时空变化外，同时通过不同的方式对蒸发能力产生影响［2］。流域总蒸发又是水量平衡的组成要素。因流域内气象条件与下垫面情况组合极为复杂，大面积范围内无法准确获得各单项蒸散发量，故目前多从综合角度估算推求流域总蒸发量。较普遍的是采用水量平衡法，即根据降水、径流、流域蓄水量的变化等资料估算；也有利用太阳辐射、降水、气温等气象要素，建立经验、半经验公式进行估算。流域总蒸发的计量单位，以时段内单位面积蒸发的水层深度（mm）表示。大范围内的流域蒸发，一般用等值线图表示其分布和变化规律。其大小受流域的热状况、水分供应条件及下垫面组成要素状况的影响。中国冬季流域蒸发量小，夏季7－9月是全年蒸发量最大的月份。就蒸发而言计算方法很多，计算公式可归纳为5类:（1）空气动力学法。空气绝热状态下，且下垫面（如土壤和植物等表面）条件均匀一致时，水汽的水平通量为零，根据分子运动理论，研究蒸发面与空气层之间的热量和水汽的乱流交换，由乱流交换系数和湿度梯度可计算出垂直水汽通量即蒸发量。（2）能量平衡法。该法是通过太阳辐射平衡计算，根据能量守恒原理求出供给蒸发的能量来确定蒸发的。上述的两种方法﹐均属于微气象学方法［2］。（3）综合方法。包括各种利用气象要素的方法，如英国彭曼法和前苏联布德克法等。目前国际上比较常用的是彭曼法。该法是从英国的自然地理条件出发提出的一种计算模型﹐考虑不同蒸发面的性质用不同的经验系数﹐可以得到比较接近实际的结果。（4）温度公式。是以气温作为蒸发计算的主要素，实际是一种纯经验的方法，其计算比较简单，但经验性强，适用性差。（5）水量平衡法。基于水量平衡的多种因子。如降水﹑径流﹑土壤湿度等平衡要素的计算。此法分为流域水文资料计算和高空气象计算两种。近年来国际上流域蒸发量计算方法发展很快，对能量和大气湍流交换进行数值模拟和利用遥感信息计算蒸发量的方法，均是极有前景的新方向。可能蒸发是蒸发计算中应用广泛的一个参数，同时可能蒸发是计算实际蒸发量的基础，可能蒸发量的准确性，直接影响实际蒸发、蒸散的结果。而可能蒸发的概念也是20世纪40年代由Thornthwaite和penman提出来的，而彭曼公式计算可能蒸发时所需要的气象资料都是常规观测资料，比较容易得到，便于使用，对蒸发能力计算方法的评估时，也认为彭曼法可用于计算各种时段的蒸发能力，且有较高精度［2］。20世纪90年代，联合国粮农组织（FAO）将Penman－Monteith公式确定为计算参考作物蒸散量（RET）的标准方法［4］。因此，本文首先采用彭曼－蒙特斯方法计算阿克苏流域气象单站的可能蒸发量，其次通过插值计算阿克苏流域可能蒸发量。客观地分析阿克苏流域可能蒸发量，可为区域生态环境治理和改善及农业可持续发展提供理论依据，对研究干旱区绿洲气候变化有参考价值。

1 资料与方法

1.1 资料

阿克苏流域内气象站较为稀少，分布也非网格状，且不均匀，为了提高计算的精确度及稳定性，我们选取阿克苏河流域及其周边站点乌什、阿克苏、温宿、拜城、新和、沙雅、库车、柯坪、阿瓦提等9个气象站。1961－2000年最高温度、最低温度、风速等气象要素日资料计算出单站日可能蒸发量，通过插值计算阿克苏流域的年平均可能蒸发量。

1.2 气象单站的可能蒸发量计算方法及其计算流域可能蒸发量插值方法

1.2.1 彭曼－蒙特斯公式的基本形式 其一般形式可表示为

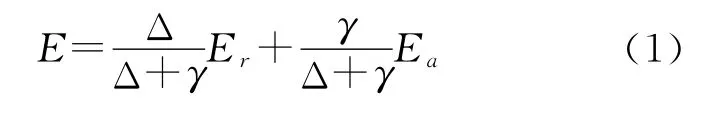
式中:Er——热力或能量过程产生的蒸发；Ea——动力作用产生的蒸发；γ——常数（0.067）；Δ——饱和水汽压曲线的斜率，而温度为t℃时的饱和水汽压可以按马格奴斯经验公式推求（近似地，不分水面与冰面，在下式中可统一取a＝17.27，b＝237.3），则其一般形式又可表示为

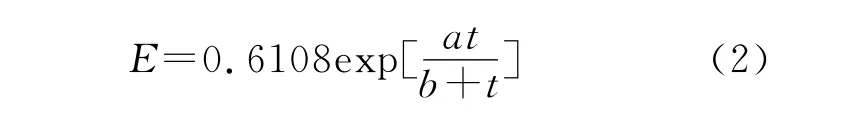
可能蒸发量或蒸发能力的计算，是在上式的基础上修订而得到的。太阳辐射是对ET0影响最大的气象要素。在没有太阳辐射及日照观测数据时，可采用下列方法补差:用本气象站的最高和最低气温观测数据计算太阳辐射。日最高气温和最低气温之差与当天的天空云量有关，而天空云量是影响太阳辐射的主要因素。Hard graves首先提出最高气温和最低气温之差与太阳辐射的关系，Allen等人修正了Hard graves方程，得到下列关系式［2］:

式中:RS——补差的太阳辐射［MJ／（m2·d）］；Ra——外空辐射［MJ／（m2·d）］；Tmax——最高温度（℃）；Tmin——最低温度（℃）；Kr——调节系数（℃－1／2）；对内陆地区通常取0.17，而对沿海地区为0.19。

Ra可由下式计算:

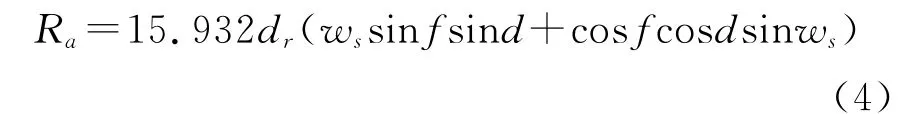
式中:dr——计算日的日地相对距离值:地球距离太阳的远点距离为1.52×108km，近点距离为1.47×108km，平均为1.5×108km；ws——太阳时角；f——测站的纬度（北半球为正值，弧度）；d——日倾角（弧角）。ws和d分别由下式计算:

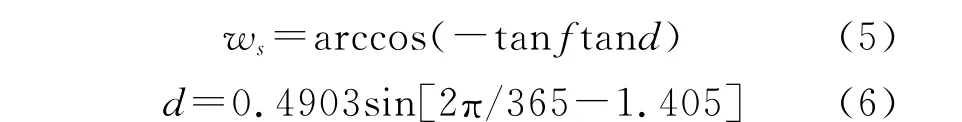
假定补差辐射即为可用于蒸发的能量，根据已有的气象理论公式，可推得可能蒸发量的计算公式:

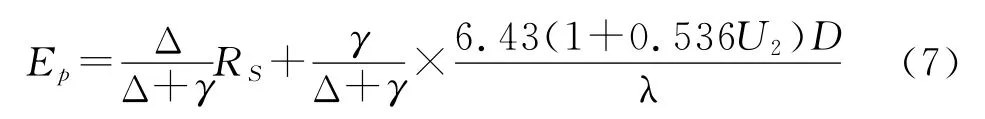
式中:λ——常数2.501；U2——2m 高的风速；D——饱和水汽压与实际水汽压之差；Rs——补差的太阳辐射。

1.2.2 其他参数假定

（1）按对数律［2］近似得到2m高的风速计算公式:

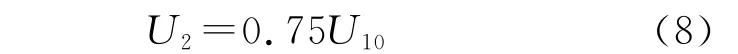
式中:U10——10～12m高度的气象站的实测风速［5］。

（2）相对湿度用来计算实际水汽压（ed）当湿度缺测或数据可靠性有问题时，实际水汽压可用最低气温（Tmin）近似计算［2］。

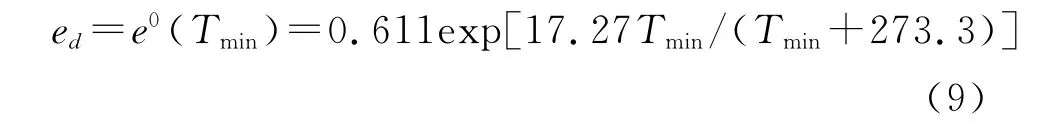
该式的基本假定条件是日最低气温（Tmin）近似等于露点温度（Tmin），即当夜间气温降至最低时，空气湿度接近饱和（RH≈100%），这对地表有草覆盖的气象站，大多数时期内是能够满足的。

Tetens公式（1930）

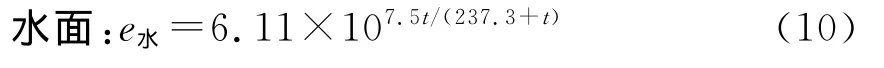
冰面与水面相比，水分子不易脱离，故冰面饱和水汽压比水面低些，满足下列经验公式:

上述公式也称为Magnus公式。在这里采用水面或者冰面公式来计算饱和水汽压与实际水汽压之差，判定条件为，当日平均温度大于或者等于0℃时，计算采用公式（10）水面公式计算水汽压差D；当日平均温度小于0℃时，计算采用（11）水面公式计算水汽压差D；

1980年Bolton给出了对Tetens公式的修正:

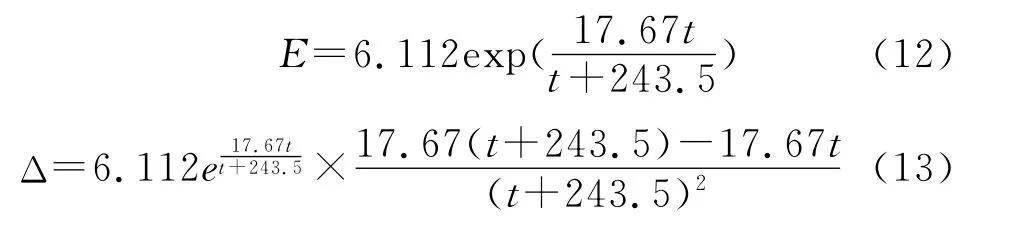
1.3 插值计算方法

以DEM数据为基础，采用梯度距离平方反比法（GIDS）作为差值公式，计算区域内每个网格点l的蒸发值E:

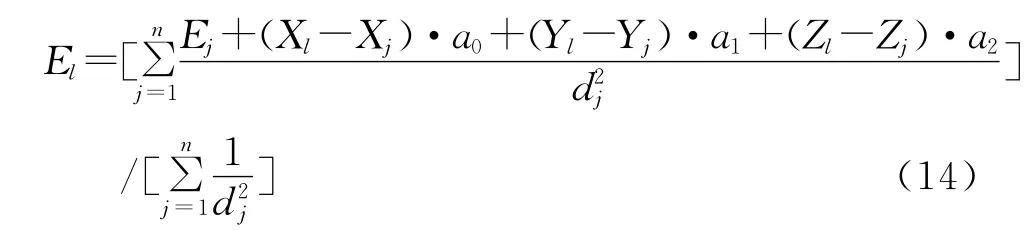
式中:Xl、Xj和Yl、Yj分别为待估点l与气象站点j的X、Y轴坐标值；Zl、Zj为待估点l与气象站点j的海拔高度；dj——待估点l与第j个气象站点的大圆距离；a0、a1、a2是蒸发量与X、Y 及海拔高度回归系数，由下式可求出:

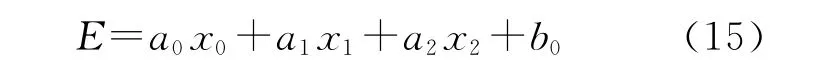
选定的参考点为（72°E，32°N），以求出气象站点和各计算点的坐标值。计算可得每个网格点的可能蒸发量。

2 结果分析

2.1 单站可能蒸发量分析

新疆属于典型的干旱区，在干旱区就普遍意义而言，可能蒸发量值很高，因为全年日照强烈，平均温度较高，因此全年降水量较少，所以其实际蒸发量不具有这么大的值，即使在湿润地区或者年降水量较大的地区也并不能时刻保证土壤有充足的水分供应条件，因此最大可能蒸发量ET只是大区域实际蒸发量的上限。

根据彭曼公式计算得到9个气象站参考蒸散发量的变化特征如表1。从表中可以看出，各个气象站1961－2000年平均可能蒸发量存在一定差别，乌什气象站海拔最高1395 .8m，可能蒸发量年均值最小（1262 .8mm）；沙雅气象站海拔最低980.4m，可能蒸发量年均值（1353 .5mm）；阿瓦提气象站海拔最低1044 .3m，可能蒸发量年均值最大（1493 .3mm）阿克苏、温宿站所在的绿洲区的可能蒸发量在1340 mm左右。就阿克苏流域单站而言，海拔高的站点可能蒸发量较小，海拔相对较低的站点可能蒸发量较大。气温随海拔高度的增加而降低，相对湿度一般随海拔高度增加而增大，所以蒸发量一般随海拔的增高而减少。随着时间序列的推移，各站的可能蒸发量年代际均值呈现递减的趋势，阿克苏单站可能蒸发量40a递减差值为34.5mm。据研究表明，从1960－2000年，由于灌溉引水的变化，阿克苏绿洲耗水量显著增大，同时绿洲年平均风速下降，年平均相对湿度增大，使绿洲年潜在蒸散发量呈显著下降趋势［2］。

在全球变暖的大背景下，国内外很多学者研究表明，很多区域的潜在蒸散发量具有显著下降的趋势［9－12］。而目前为止对潜在蒸散发下降的影响因素已有较多研究［12－14］，一方面认为潜在蒸散发的下降主要受到辐射和风速等自然因素变化的影响［14－15］，另一方面则认为潜在蒸散发的下降是陆面实际蒸散发增大的结果，与区域水文循环的变化有着紧密联系，且受到人类活动的显著影响。虽然潜在蒸散发量与本文所计算的可能蒸发量的概念有所区别，但是随时间序列的变化趋势大致相同，而影响蒸发的气象要素主要是温度、风速、湿度、辐射的变化，我们计算的可能蒸发量更接近实际蒸发量，但并不是实际蒸发量，而是实际蒸发量的上限。而潜在蒸散发是各个气象站蒸发皿观测值，只是蒸发反映了单站或者区域的蒸发能力的大小，因此，本文计算的可能蒸发量更具有实际意义。通过单站40a潜在蒸散发的观测值和计算值对比，观测值明显大于计算值，差值区间为110～1255 mm，总体来看，其中海拔较低阿瓦提、温宿、阿克苏差值较小，海拔较高的乌什、库车、柯平差值较大。说明计算值在海拔相对较低的区域精度较高，在海拔较高的区域差值相对较大。

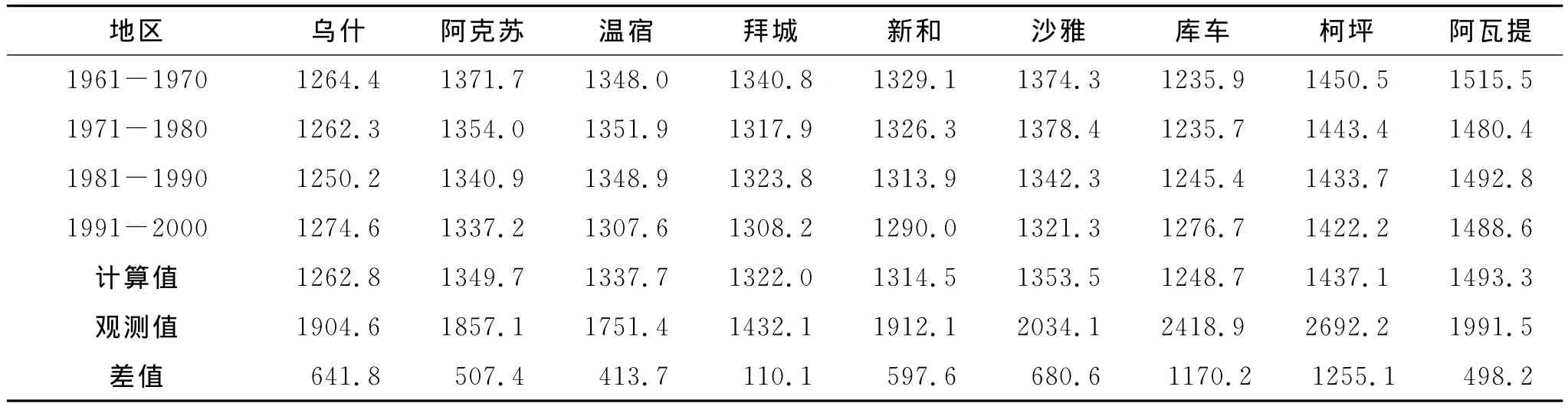
表1 单站40a潜在蒸散发观测均值和可能蒸发量年均值 mm

2.2 阿克苏流域的年平均可能蒸发量分析

由图1可知，阿克苏流域可能蒸发量分布不均匀，整个流域靠近天山山脉的托木尔峰附近可能蒸发量最小，年均值约在600mm左右，阿拉尔以及阿瓦提一带可能蒸发量最大，年均值约在1400 mm以上，最大地区可达1600 mm。流域的西南至东北一带可能蒸发量较小约在1000 mm以下，流域东南部阿克苏以及温宿一带年均值可能蒸发量也较大，约在1400 mm左右，流域中部阿合奇、乌什一带可能蒸发量年均值也达到了1200 mm，整个流域西部可能蒸发量年均值在1000 mm左右，流域北部的可能蒸发量年均值分布比较均匀，约为800～1000 mm，靠近天山南坡的部分地区随着海拔的上升，平均温度的下降，可能蒸发量的年均值达到700mm左右，整个流域天山山区附近一带可能蒸发量要明显小于流域以内靠近塔里木盆地的天山南坡的山前冲积平原地区，可能蒸发量的总体变化趋势是随着海拔高度的降低而逐渐增大。计算整个阿克苏流域年平均可能蒸发量约为848.3亿 m3。

阿克苏、温宿至阿拉尔一带可能蒸发量较大在1400 mm以上，阿克苏流域北部山区可能蒸发量较小，特别是东北部的山区的可能蒸发量最小，基本上在800mm以下。可能蒸发量是温度和风速的函数，温度是水汽传播速度及水汽接纳能力的影响要素，风速的大小影响了对紊流扩散的强度和干湿空气的交换速度，山区温度远远低于阿克苏流域西部及东南部阿克苏－阿拉尔一带。虽然阿克苏流域天山山区一带，早晚山谷风较其他地区较大，但是干湿空气之间的差异很小，这取决于新疆本身的地理因素。但应指出，由于风速是随高度增加而增大的，因此蒸发量随着海拔增加而递减的速度便大大减小，此外，由于山区地形变化，也导致蒸发量随着海拔增加而变小，但总的来说，这些都是次要或局部的因素，而主要是蒸发量随海拔增高而递减。所以在阿克苏流域风速对可能蒸发量的影响要小于海拔变化和温度的影响。因此，在阿克苏流域，海拔高差变化和温、湿度是影响可能蒸发量大小的主要因素。

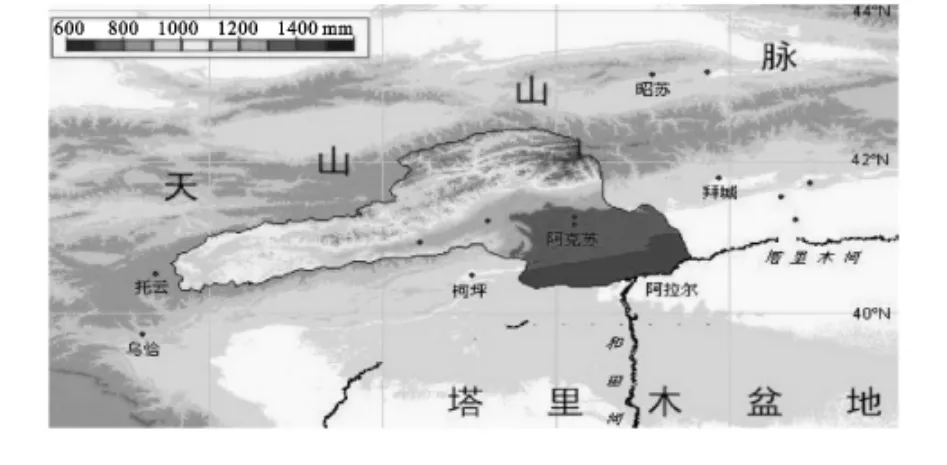
图1 阿克苏流域可能蒸发量分布图

3 结论

（1）阿克苏流域年平均可能蒸发量约为848.3亿m3，且分布不均匀，最大值达到1600 mm，最小值约为600mm。可能蒸发量的总体变化趋势是随着海拔高度的降低而逐渐增大，随着平均温度的增大而逐渐增大。就单站而言，海拔高的站点可能蒸发量较小，海拔相对较低的站点可能蒸发量较大。观测值和计算值对比，海拔低的区域精度高，海拔高的区域精度低。

（2）虽然阿克苏流域山谷风环流明显，但是由于流域当地空气中湿度差异不大，干湿空气交换不如降水量充分的地区。因此，风速对可能蒸发量的影响要明显小于温度。在阿克苏流域，海拔高差和温、湿度的变化才是影响可能蒸发量大小的主要因素。

（3）整个阿克苏流域的可能蒸发量很大，但是实际蒸发量的值却很小，这主要取决于空气中的水汽含量和下垫面的水分条件，虽然阿克苏流域和天山南坡年降水量要大于南疆大部分地区，但是相对于蒸发能力而言，却微乎其微。因此，可能蒸发量只是阿克苏流域区域实际蒸发量的区间上限。

［1］刘小莽，郑红星，刘昌明，等.海河流域潜在蒸散发的气候敏感性分析［J］.资源科学，2009，31（9）:1470－1476.

［2］Kundzewicz Z W，Somlyody L.Climatic Change Impact on Water Resources in a Systems Perspective［J］.Water Resour.Manage.，1997，11:407－435.

［3］布德科 M N.地表面热量平衡［M］.李怀瑾，邓进上，译.北京:科学出版社，1960.

［4］钱学伟，李秀珍.陆面蒸发计算方法述评［J］.水文，1996（6）:25－31.

［5］Allen R G，Pereira L S，Raes D，et al.Crop Evapotranspiration:Guidelines for Computing Crop Water Requirements［M］.Rome:Food and Agriculture Organization of the United Nations，1998.

［6］刘钰，Pereira L S，Teixeira J L.参照腾发量的新定义及计算方法对比［J］.水利学报，1997，28（6）:27－33.

［7］傅抱璞，翁笃鸣，虞静明，等.小气候学［M］.北京:气象出版社，1994:126－127.

［8］韩松俊，胡和平，杨大文，等.塔里木河流域山区和绿洲潜在蒸散发的不同变化及影响因素［J］.中国科学:E辑，2009，39（8）:1375－1383.

［9］Gao G，Chen D L，Xu C Y，et al.Trend of estimated actual evapotranspiration over China during 1960－2002［J］.J.Geophys.Res.，2007，112，D11120［doi］.

［10］Ohmura A，Wild M.Is the hydrological cycle accelerating［J］.Science，2002，298（5597）:1345－1346.

［11］邱新法，刘昌明，曾燕.黄河流域近40年蒸发皿蒸发量的气候变化特征［J］.自然资源学报，2003，18（4）:437－442.

［12］左洪超，李栋梁，胡隐樵，等.近40年中国气候变化趋势及其同蒸发皿观测的蒸发量变化的关系［J］.科学通报，2005，50（11）:1125－1130.

［13］Zhang Y Q，Li C M，Tang Y H，et al.Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau［J］.J.Geophys.Res.，2007，112:D12110［doi］.

［14］Roderick M L，Rotstayn L D，Farquhar G D，et al.On the attribution of changing pan evaporation［J］.Geophys Res.Lett.，2007，34:L17403［doi］.

［15］Ozdogan M，Salvucci G D.Irrigation－induced changes in potential evapotranspiration in southeastern Turkey:Test and application of Bouchet＇s complementary hypothesis［J］.Water Resour Res.，2004，15:443－450.