轻便导线接继器的强度校核

彭朝晖

（湖南新成机器有限责任公司，湖南株洲 412007）

轻便导线接继器的强度校核

彭朝晖

（湖南新成机器有限责任公司，湖南株洲 412007）

轻便导线接继器是电力输送向前发展的产物，将它代替传统的电线接头，有方便、简捷、承载力大、美观等特点。以LGI－70轻便导线接继器为例，进行强度校核。

轻便导线接继器;LGI－70轻便导线接继器;强度校核

轻便导线接继器是电力输送向前发展的产物，将它代替传统的电线接头，有方便、简捷、承载力大、美观等特点。根据电缆线的不同，接继器的型号也多种多样，在此以LGI－70轻便导线接继器为例，进行强度校核，其他型号的接继器可参考本文计算进行强度设计。图1为LGI—70轻便导线接继器简图。

图1 LGI—70轻便导线接继器简图

根据接继器装配结构可知，接继器强度计算应包括如下内容：夹爪强度分析、壳体直径部应力集中处（16—SR2）强度校核、壳体锥面强度校核。

1 夹爪强度校核

夹爪通过齿面与导线咬合，在外载作用下两者紧固于一体，在紧密接触区发生固相焊合，形成“冷焊”结点，此时夹爪与导线可视为一个整体，显然联合体的强度必定大于导线的强度。而根据强度校核的条件，要求导线实际拉力（N实）小于计算拉力（许用拉力）才能进行校核结构的强度。由上分析可知，夹爪强度一定符合要求。［1］

2 壳体直径部应力集中处（16—SR2）强度校核

已知：壳体直径部内径r1=15．5mm，外径r2= 17．5mm，铝管LY11，σs=108～206MPa，σb=206～412MPa。计算得拉力F=23390N，应力集中处小窝球面半径SR=2mm。

而横截面积A=π（r22－r12），代入数据得A= 207．24mm2，壳体受拉正应力σ=F/A=112．86MPa。

参考机械设计轴上环槽处理论应力集中系数，SR/r2=2/17．5=0．114，D/d=17．5/15．5=1．13。

又16孔小孔均布，取Kσ=1．5，则［σ］=σs/ Kσ=108～206/1．5=72～137．3MPa，因而［σ］＜σs，可看出当外载达到许用拉力时壳体可能产生塑性变形。

但［σ］b=σb/Kσ=206～412/1．5=137．3～274．7，得［σ］b＞σ。

由于［σ］＜σ＜［σ］b，可见，在外载作用下壳体直径部处于弹塑性状态。［2］

3 壳体锥面强度校核

因为壳体锥面外力来自夹爪提供的摩擦力，而夹爪在工作状态下并非理想圆柱形，所以提供给壳体的力仅是轴对称分布，而在壳体部分分布并不均匀，故为计算方便，须作如下假设：

1）壳体锥面形状为理想的圆锥筒形;

2）材料是匀质和各向同性的;

3）锥筒承受的径向力计算时按均匀分布，但在实际情况下须考虑力分布不匀影响系数。

在工作状态下为静载荷，各质点处于静力平衡状态。［3］

假设壳体承载情况下受外力为F，则：

沿锥面切线方向分力P1=Fcosθ

沿锥面法线方向分力P2=Fsinθ

夹爪锥面面积S=πl（R+r）

其中：l——锥面母线长，R——大头半径，r——小头半径。

将P1、P2化为单位面积上受力，得：

其中：F——外载荷力（N），r1、r2——接触面任一截面处内、外半径，l——夹爪母线长。

取接触面上某截面进行分析，沿锥面切线方向应力为：

对于沿锥面法线方向应力，先沿锥面法线建立坐标系，如图2所示，P2为正压力，R、r+dr为相邻两圆柱面半径，dθ为两相邻径向面夹角，abcd为任取单元体，u、u+du为单元体沿法面位移。

图2 应力示意图

因为变形对圆锥轴线是对称的，所以筒内各点沿法线方向位移u只与r有关，与θ无关。

变形后单元体ad移至a`d`，得周向应变为：

（1）中又因位移u是r的函数，在ab边上a的径向位移为a，则b的径向位移为u+du。［4］

a点沿半径方向的应变为：

考虑静力平衡关系，如图3所示。σr为法向应力，σθ为周向应力。

图3 截面应力关系图

据轴对称性质，同样σr、σθ都只是r的函数与θ无关。

将作用于单元体上的应力投影于r轴上得：

将边界条件代入（9）式解得A、B，并代回（9）式，得应力计算公式：

以LGI—70接继器为例，代入数据作强度校核分析。

已知：F=23390N，θ=2．5°，P2=Fsinθ/S= Fsinθ/πl（R+r），其中R、r分别为夹爪与壳体接触面两端半径，l为夹爪母线长。

据实测，夹爪小头端面至壳体小头端面距离为65mm，再根据壳体零件可得：

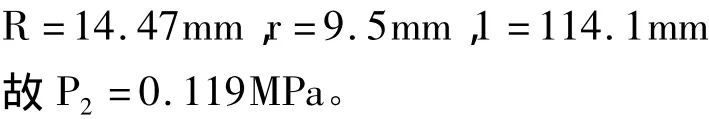
因为在r=r1处σθ、σr都是同时达到极值，如图4所示。

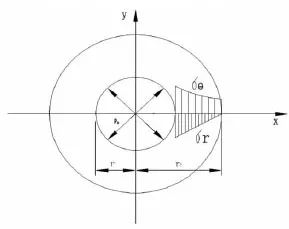
图4 截面应力分布图

σθ、σr在r=r1处达到极值后，若外力再增大，则壳体从内至外将逐渐由弹性状态到弹塑性状态，再到完全塑性状态，最后破裂。［5］

故此取r=r1（即假设处于弹性），则（11）式变为：

小头强度校核：距壳体端面65mm处，r1=9．5mm =r，r2=13mm。

将各已知条件代入（12）式得：

στ=94．46MPa，σθ=0．392MPa，σr=－0．119MPa

根据第四强度理论公式，令σ1=στ，σ2=σθ，σ3=σr，可得：

代入数据σca=94．32MPa，其中σca为计算应力。

因LY11铝管σs=108～206MPa，可得：

大头接触处强度校核，可知r1=14．47mm，由零件图可算出r2=18mm。

将已知条件代入（12）式得：

根据第四强度理论公式，令σ1=στ，σ2=σθ，σ3=σr，代入数据可得σca=64．52MPa。

因LY11铝管σs=108～206MPa，可得：

4 结论

综合以上三项强度分析，可看出：

1）壳体直径部（包括应力集中处）强度基本合格，但当外载达到计算拉力时，壳体可能处于弹塑性状态，甚至引起塑性变形。

2）壳体锥面强度，接触部分从小到大强度逐渐升高，但均可满足要求。

因此，可以论证壳体结构合理，锥面角度θ选择恰当，尺寸选择可达到设计要求。

［1］程光仁，潭仪容．机械设计［M］．南京：南京理工大学出版社，1993．

［2］刘鸿文．材料力学［M］．北京：高等教育出版社，2004．

［3］全国术语标准化技术委员会．GB 1179－83［S］．北京：全国术语标准化技术委员会，1983．

［4］吴宗泽．机械设计实用手册［M］．北京：化学工业出版社，2010．

［5］邱关源．电路分析［M］．北京：高等教育出版社，2006．

［编校：邓桂萍］

The Strength Check of Portable W ire Relay Device

PENG Zhaohui
（Hunan Xincheng Machine Co．，Ltd．，Zhuzhou Hunan 412007）

As the product of the development of electric power，the portable wire relay device is characterized by its convenience，simplicity，aesthetic appearance，high bearing capacity，etc．，so it can replace the traditionalwire joint．This paper uses LGI－70 lightwire relay device as an example to check the strength．

portable wire relay device;LGI－70 lightwire relay device;strength check

F273．7

A

1671－9654（2011）04－055－04

2011－11－15

彭朝晖（1969－），男，湖南宁乡人，工程师，研究方向为机械设计与制造。