地震作用对钢桁梁桥车桥系统耦合振动的影响分析

邓子铭，郭向荣，张志勇

(中南大学 土木建筑学院，湖南 长沙，410075)

地震作用对钢桁梁桥车桥系统耦合振动的影响分析

邓子铭，郭向荣，张志勇

(中南大学 土木建筑学院，湖南 长沙，410075)

为了研究地震对车桥系统耦合振动的影响，采用最小二乘法对地震加速度进行校正拟合，消除位移时程因直接对加速度时程积分出现的漂移现象。根据弹性系统动力学总势能不变值原理及形成矩阵的“对号入座”法则，将轨道不平顺作为系统的自激激励源，地震作为外部激励，建立考虑地震作用的车桥系统耦合振动方程。并以某钢桁梁桥为例，采用计算机模拟的方法，建立列车和桥梁动力分析的有限元模型，研究地震对车桥系统耦合振动的影响。研究结果表明：在地震作用下，桥梁的动力响应主要取决于地震力，横向地震波对车辆与桥梁的横向动力响应具有非常重要的影响；竖向地震波主要影响车桥系统的竖向振动，对横向振动影响很小；但是，竖向地震波对脱轨系数、轮重减载率、车体竖向加速度的影响较显著，因此，在评判桥上列车的运行安全性时必须考虑竖向地震波的影响。

钢桁梁桥；地震加速度；漂移现象；耦合振动；有限元模型；动力响应

长期以来，地震荷载作用下的车−桥系统动力相互作用问题，常常被分为“桥梁抗震”和“车−桥耦合振动”2个相对独立的研究领域。前者以桥梁为主体，将列车荷载作为移动荷载或不考虑列车荷载，研究桥梁的地震响应；后者则不考虑地震荷载的影响，仅研究列车和桥梁之间的动力相互作用[1−4]。为保证线路的平顺性和稳定性，高速铁路上可能需要建造连续几公里甚至更长的桥梁工程，这样，地震发生时列车在桥上的概率就会大为增加，一旦列车在地震中脱轨，就会带来巨大的财产损失并会危及到乘客的生命安全[3,5−8]，因此，有必要对地震作用下的列车走行性进行研究。在此，本文作者在前人对时域优化校正算法研究的基础上，采用最小二乘法对地震加速度进行校正拟合，消除位移时程因直接对加速度时程积分出现的漂移现象。并根据弹性系统动力学总势能不变值原理[9]及形成矩阵的“对号入座”法则[10]，将轨道不平顺作为系统的自激激励源，地震作为外部激励，建立考虑地震作用的车桥系统耦合振动方程。以郑州黄河桥为例，采用计算机模拟的方法，建立列车和桥梁动力分析的有限元模型，对地震时桥上列车的走行性进行研究，分析地震对车桥系统耦合振动的影响。

1 车桥系统的力学模型

1.1 车辆计算模型

计算车辆由车体、转向架和轮对3个部件组成，见图1。车体有侧摆、侧滚、摇头、点头、浮沉共5个自由度；每个构架有侧摆、侧滚、摇头、浮沉共4个自由度；每个轮对有侧摆、浮沉共2个自由度。每辆车(包括机车)的计算模型由1个车体、2个转向架和4个轮对组成，共有21个自由度[11]。并遵循以下基本假定：(1) 车体、转向架和轮对均假设为刚体；(2) 不考虑机车、车辆纵向振动及其对桥梁振动与行车速度的影响；(3) 轮对、转向架和车体均作微振动；(4) 所有弹簧均为线性，所有阻尼按黏性阻尼计算，蠕滑力按线性计算；(5) 沿铅垂方向，轮对与钢轨密贴，即轮对与钢轨的竖向位移相同；(6) 忽略构架点头运动及轮对侧滚和摇头运动。

1.2 桥梁计算模型

桥梁采用空间梁−杆系有限元分析模型。对空间梁单元模型，采用二节点空间直梁单元，考虑其竖向、横向受弯以及扭转变形，每个节点考虑3个线位移与3个转角位移，整个单元有12个自由度；对空间杆单元模型，每个节点考虑3个线位移，整个单元有6个自由度；桥墩均采用空间梁单元模拟。梁与墩之间的联结根据实际约束条件采用主从关系来处理，梁体和桥墩之间以主从节点的方式相连。墩底处地基基础的刚度分别叠加于相应的节点上。桥梁系统的阻尼按Rayleigh阻尼考虑，低阶频率对应的阻尼比一般取2%～5%；弹性模量E和泊松比μ按现行桥规取值，二期恒载作为均布质量分配到相应的桥梁单元中。

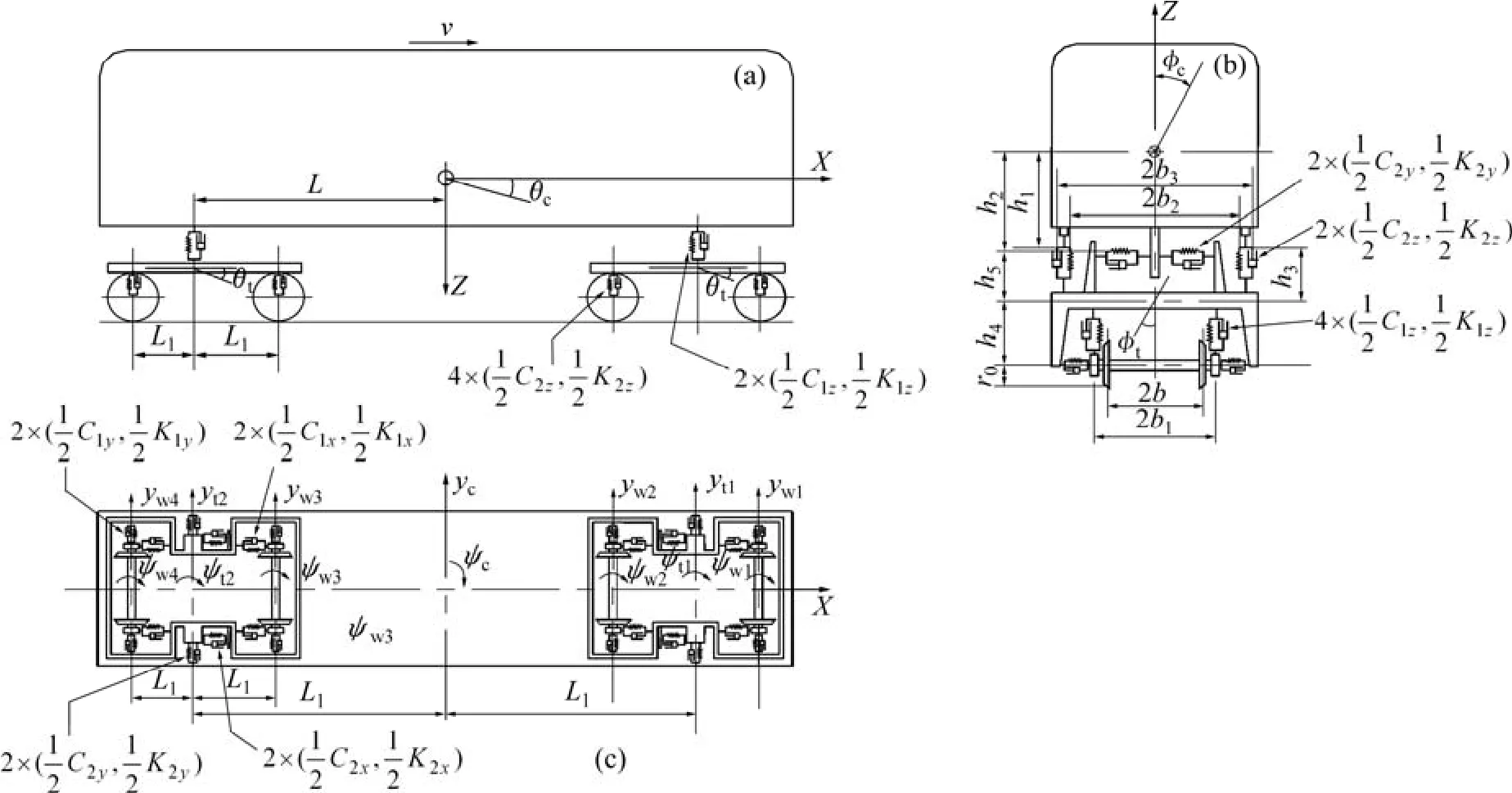
图1 车辆计算模型Fig.1 Mechanical model of vehicle

2 地震作用下车桥耦合振动方程的建立与求解

地震荷载作用下车−桥耦合系统振动分析模型是将列车和桥梁视为一个整体系统，将轨道不平顺作为系统的自激激励源，将地震荷载作为外部激励作用在桥梁支承处。把整个车桥体系的运动方程按结构非支承节点和地面支承节点分块，则在各支承处受到不同的地面运动激励作用时，地震作用下的车桥系统运动方程可写为[12−13]：

基于拟静力位移的概念，多点激振下的桥梁结构总位移方程和支承点力的平衡方程代入方程(1)，并采用集中质量矩阵表示为：

支承反力可由下式计算得到：

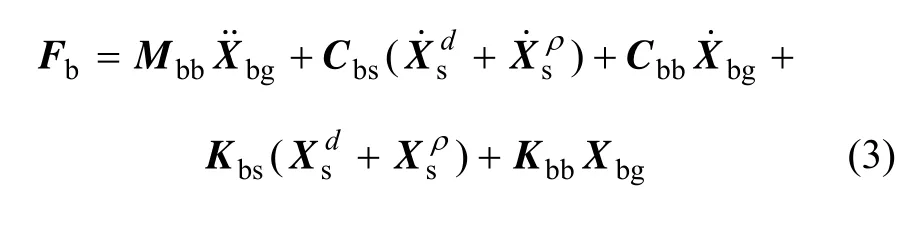
一致地震动输入假定桥梁所有桥墩墩底受到的地震激励均相同，即各支承点的相对位移为 0。此时影响矩阵为单位矩阵Rsb=I，若忽略地面速度向量产生的阻尼力(阻尼力对上式右端项的贡献很小)，运动微分方程经变换退化为经典的结构动力方程：

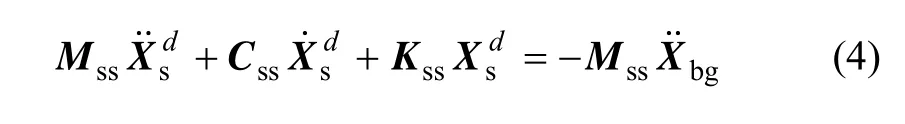
式(4)即为不考虑行波效应和多点激励时的桥梁结构地震动微分方程。

本文应用Wilson-θ逐步积分法直接求解地震荷载作用下车−桥耦合系统振动方程。

3 地震波的修正

在地震作用下的车桥耦合振动计算过程中，除了要考虑地震加速度时程外，还要考虑地震动的速度和位移时程。然而，由于目前地震记录一般仅提供加速度信息，获得的地震波数据大都是以加速度时程的形式给出。合成人工地震波也只是生成加速度波信息，因此，地震动速度与位移时程需要通过积分地震加速度获得。但是，如果直接对加速度时程二次积分得到的位移时程则会出现漂移现象，这是因为在加速度时程合成计算中，尽管采取了一定的修正手段(例如零线校正法)，一些长周期分量仍然会残留下来，它们虽然不会导致加速度时程的漂移，但是会对积分后的位移时程产生严重的漂移[14]。用这样的位移时程进行计算，将会导致计算结果失真。许多学者对此进行了广泛的研究，认为加速度时程中的少量长周期分量是导致位移时程漂移的主要原因。

本文在前人对时域优化校正算法研究的基础上，采用最小二乘法对加速度进行校正，按照位移点在均值线两侧分布均匀和多项式阶数尽可能低的准则，采用三次多项式对加速度的均值线进行校正，然后，对修正后的加速度进行2次积分计算，得到速度时程和位移时程。这样，在输入的加速度时程中减去相应的最小二乘法拟合的三次多项式均值线，不仅可以从根源上消除位移非零漂移值，方便工程的应用，而且避免了仅对积分位移作高通滤波处理后对加速度、速度和位移之间积分关系的破坏。

本文对该桥100 a超越概率为3%的人工合成地震加速度、速度和位移时程进行拟合修正，修正后的地震时程曲线如图2～4所示，然后，将地震波输入车桥系统进行计算。

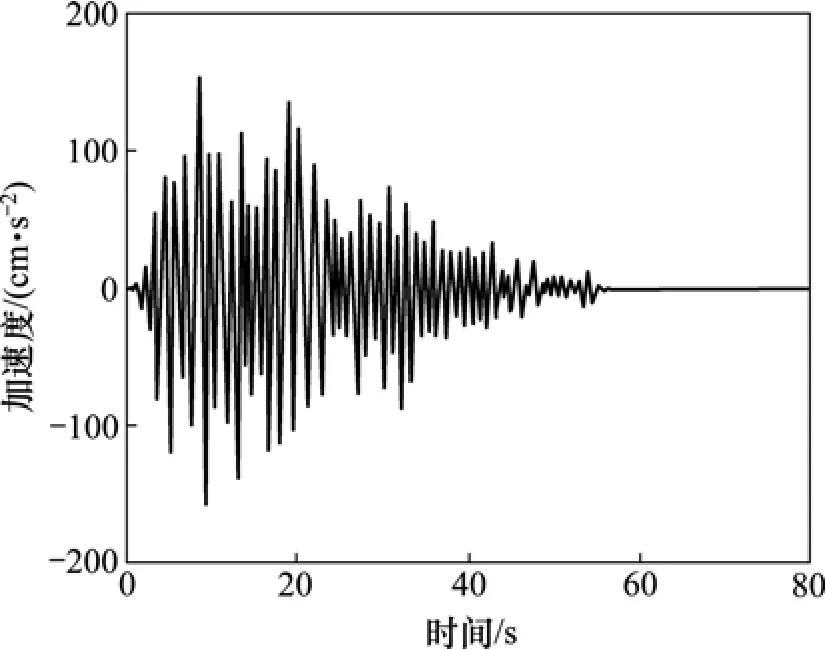
图2 地震加速度时程曲线图Fig.2 Curve of seismic acceleration

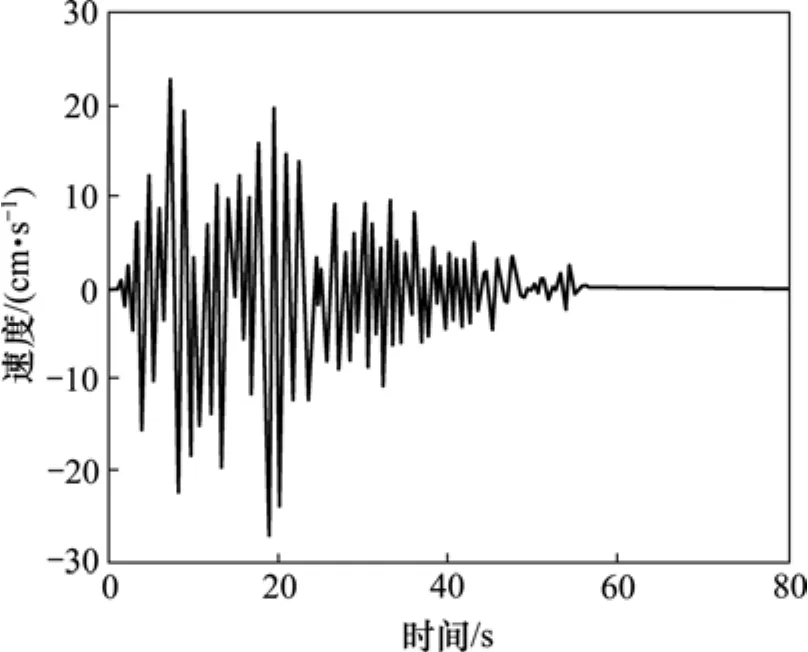
图3 地震速度时程曲线Fig.3 Curve of seismic velocity

图4 地震位移时程曲线Fig.4 Curve of seismic displacement

4 工程背景

郑州黄河公铁两用桥主桥全长1 684.35 m，共2联，这里以第2联为例进行分析研究。第2联是长度为5×120 m 的连续钢桁结合梁桥。该桥主要结构示意图如图5所示。上层公路桥面宽32.5 m，下层铁路桥面为双线客运专线，线间距 7 m。主桁为三角形桁式，横向布置3片桁，中桁垂直，边桁倾斜。主桁桁高14 m，节间长度为12 m。钢桁梁上弦杆与混凝土桥面板结合形成公路结合桥面，下层铁路桥面为正交异性整体钢桥面板，其上面铺设混凝土道碴槽桥面板。公路混凝土桥面板纵横向均为全预应力结构。 主桥采用球形支座，纵向仅在8号墩顶边、中桁处设置纵向限位支座，其余为纵向活动支座；横向仅在中桁下设置横向限位支座，边桁为横向活动支座。

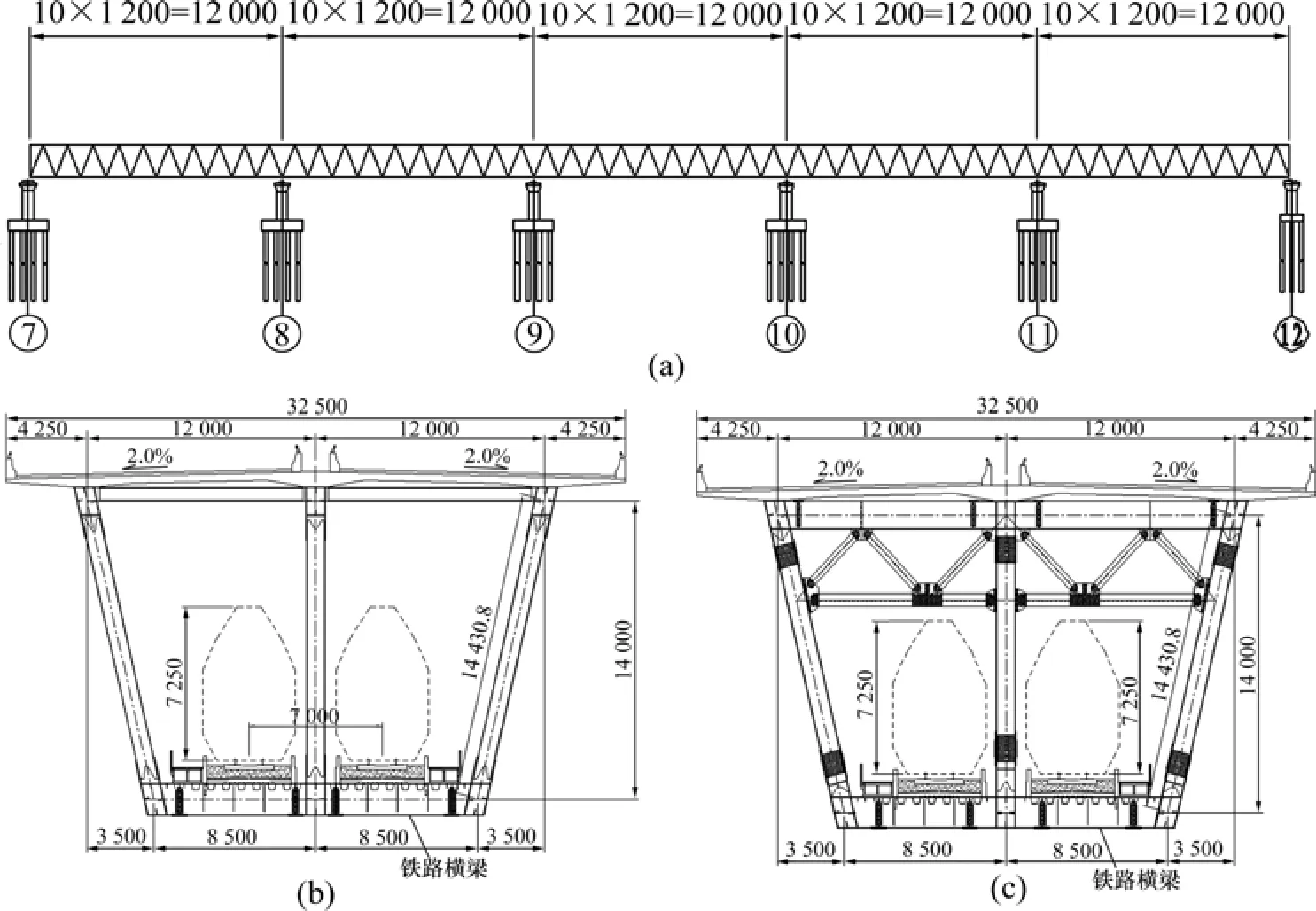
图5 郑州黄河桥结构示意图(单位：cm)Fig.5 Structural diagram of Yellow River Bridge

5 地震作用对车桥系统耦合振动的影响分析

5.1 计算工况

根据前述计算模型与计算原理，对连续钢桁梁桥进行地震作用下列车−桥梁时变系统空间振动响应计算。计算中列车采用德国ICE高速列车，其16辆列车编组为：4辆动车+2辆拖车+4辆动车+2辆拖车+4辆动车，速度分别取200，250，300和350 km/h，轨道不平顺采用德国低干扰谱。横向地震波分别选取该桥100 a超越概率为3%的人工合成地震加速度、速度和位移时程，竖向地震波取横向地震波的65%，将横向和竖向的地震波输入车桥系统进行计算。计算步长取0.005 s，阻尼比为3%。为了对比分析，本文也计算了该桥无地震作用下的车桥动力响应。

5.2 计算结果及分析

将同时考虑横向和竖向地震波影响的所有计算工况的车桥系统动力计算结果列于表1和表2。图6所示为无地震和有地震作用下桥梁跨中桥面节点动位移响应的时程曲线。

由表1、表2和图6可以看出：有地震作用下桥梁跨中竖向位移和横向位移比无地震要大很多，且随着地震强度的增大，位移响应增加很明显；地震对桥梁横向位移的影响要比竖向位移的影响显著，地震作用时车辆响应的各指标值均大于无地震作用时的相应值，这表明地震荷载会直接导致行车安全性下降。

表1 桥梁跨中桥面节点最大动位移响应Table 1 Maximum dynamic response of bridge

表2 车辆各指标振动响应的最大值Table 2 Maximum dynamic responses of cars

图6 v=350 km/h时桥梁的横向和竖向位移时程曲线Fig.6 Lateral and vertical displacement curves of bridge When v is 350 km/h

5.3 横向地震波的影响

为了研究地震波对列车的走行性影响，把上面的横向地震波强度分别按照0.05g，0.1g，0.15g，0.2g，0.25g，0.3g(g为重力加速度，g=9.8 m/s2)进行规格化处理，计算列车在300 km/h的速度下的动力响应，对列车的走行性进行研究。表3所示为地震波强度和桥面横向位移、横向加速度、竖向加速度、列车脱轨系数、轮重减载率、横向轮轨力、车体横向加速度和车体竖向加速度的影响。

从表3可以看出：随着横向地震波强度的增大，桥梁的横向位移、横向振动、列车脱轨系数、轮重减载率、横向轮轨力、车体横向加速度均按线性规律增长；随着桁架桥梁横向振动的加剧，桁架桥梁的扭转也加剧，因此，桥梁和车体的竖向振动也增大。相对横向振动来说，横向地震波对车辆和桥梁的竖向振动影响稍弱。以上结果说明：横向地震波强度对车辆与桥梁的横向动力响应具有非常重要的影响。地震波强度越大，相应的桥梁和车辆的动力响应越大，车辆的振动加速度、轮轨力和脱轨系数都显著增大，车辆运行也越不安全。

5.4 竖向地震波的影响

一般认为，竖向地震波对桥梁的影响不大。因为竖向地震导致桥梁上下振动，这个振动增加了桥墩的轴向力。而桥墩的轴向力一般安全储备比较大，因此，竖向地震波对桥梁的作用不被关注。我国的《铁路工程抗震设计规范》规定验算铁路工程的抗震强度、变形、稳定性时，一般只计横向地震的作用；设计烈度为9度的悬臂结构和预应力混凝土刚构桥等，应计入竖向地震的作用。然而，竖向地震波导致桥梁上下振动，自然会导致影响到车辆的行走特性；因此，要研究地震对列车在桥上的走行性影响，竖向地震的影响是不可忽略的。

为了研究地震下竖向地震波的影响，对竖向地震波的影响规律进行模拟计算。计算中模拟车辆的速度为 300 km/h，改变竖向地震波的幅值，结果如表 4所示。

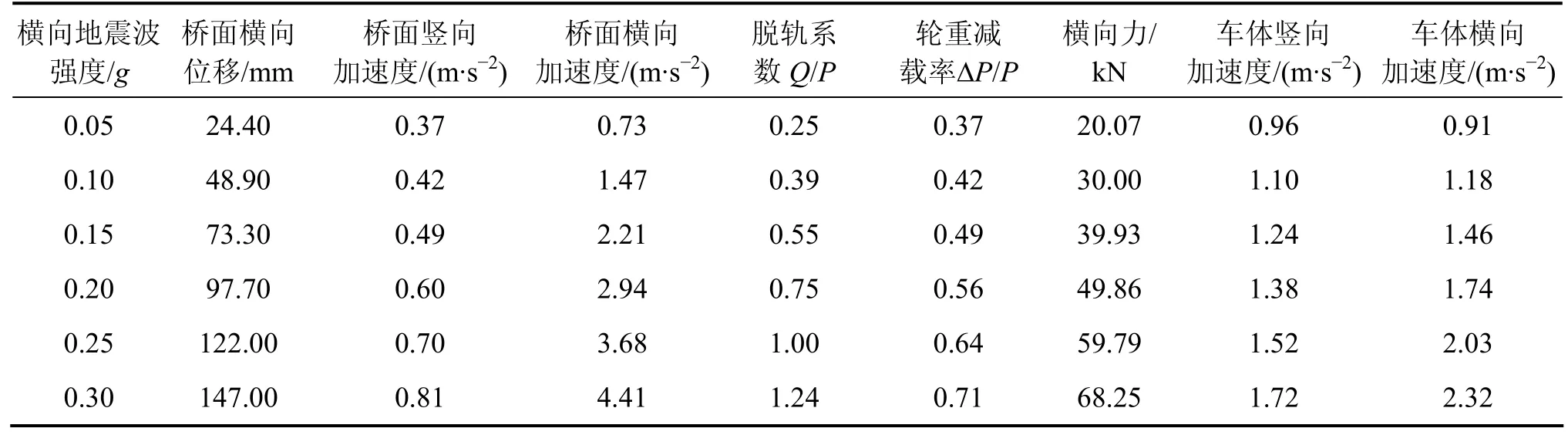
表3 横向地震波强度对列车、桥梁动力响应的影响Table 3 Influence of lateral seismic intensity on train, bridge dynamic responses

表4 竖向地震波强度对列车、桥梁动力响应的影响Table 4 Influence of vertical seismic intensity on train, bridge dynamic responses

从表4可以看出：随着竖向地震波强度的增加，桥梁的竖向振动增加显著，而横向振动只有微弱增加；对车辆来说，随着竖向地震波的增加，车辆脱轨系数、轮重减载率、车体竖向加速度也增加，轮轨横向力、车体的横向加速度变化不大；因此，竖向地震波主要影响车桥系统的竖向振动，对横向振动影响很小。

从桥上列车的走行性上评价来说，竖向地震波对脱轨系数、轮重减载率、车体竖向加速度影响比较显著，因此，考虑竖向地震波时对桥上列车的运行安全性上评判更加准确。

6 结论

(1) 在前人对时域优化校正算法研究的基础上，在输入的加速度时程中减去相应的最小二乘法拟合的三次多项式均值线，消除了位移时程因直接对加速度时程积分出现的漂移现象，方便工程应用。

(2) 在地震作用下，桥梁的动力响应主要取决于地震力，横向地震波对车辆与桥梁的横向动力响应具有非常重要的影响。

(3) 竖向地震波主要影响车桥系统的竖向振动，对横向振动影响很小。但是，竖向地震波对脱轨系数、轮重减载率、车体竖向加速度的影响较显著，因此，在评判桥上列车的运行安全性时必须考虑竖向地震波的影响。

[1] 阎贵平, 夏禾, 陈英俊. 铁路斜拉桥的地震响应特性研究[J].北方交通大学学报, 1995, 19(2): 137−142.

YAN Gui-ping, XIA He, CHEN Ying-jun. Seismic response characteristics of railway cable-stayed bridges[J]. Northern Jiaotong University, 1995, 19(2): 137−142.

[2] 王贵春, 潘家英. 铁路桥梁在列车荷载作用下的动力分析[J].中国铁道科学, 1996, 17(4): 80−89.

WANG Gui-chun, PAN Jia-ying. The method of dynamic analysis for railway bridge under the action of vehicle[J]. China Railway Science, 1996, 17(4): 80−89.

[3] 张楠, 夏禾. 铁路桥梁在高速列车作用下的动力响应分析[J].工程力学, 2005, 22(3): 144−151.

ZHANG Nan, XIA He. Dynamic analysis of railway bridge under high speed train[J]. Engineering Mechanics, 2005, 22(3):144−151.

[4] 徐植信, 胡再龙. 结构地震反应分析[M]. 北京: 高等教育出版社, 1993: 80−84.

XU Zhi-xin, HU Zai-long. Analysis of structures under earthquake[M]. Beijing: Higher Education Press, 1993: 80−84.

[5] 向俊, 杨军祥, 赫丹, 等. 焦柳线酉水大桥上货物列车脱轨分析[J]. 中南大学学报: 自然科学版, 2006, 37(1): 169−175.

XIANG Jun, YANG Jun-xiang, HE Dan, et al. Derailment analysis of freight train on Youshui Bridge on Jiaoliu line[J].Journal of Central South University: Science and Technology,2006, 37(1): 169−175.

[6] 夏禾. 车辆与结构动力相互作用[M]. 北京: 科学出版社,2002: 118−134.

XIA He. Dynamic interaction between vehicles and structures[M]. Beijing: Science Press, 2002: 118−134.

[7] Xia H, Xu Y L, Chan T H T. Dynamic interaction of long suspension bridges with running trains[J]. Journal of Sound and Vibration, 2000, 237(2): 263−280.

[8] 李小珍, 强士中. 大跨度公铁两用斜拉桥车桥动力分析[J].振动与冲击, 2003, 22(1): 6−9.

LI Xiao-zhen, QIANG Shi-zhong. Vehicle-bridge dynamic analysis for long span rail-cum-road cable-stayed bridge[J].Vibration and Shock, 2003, 22(1): 6−9.

[9] 曾庆元, 郭向荣. 列车桥梁时变系统振动分析理论与应用[M].北京: 中国铁道出版社, 1999: 35−150.

ZENG Qing-yuan, GUO Xiang-rong. Theory and application of train-bridge time-variant system vibration analysis[M]. Beijing:China Railway Press, 1999: 35−150.

[10] 曾庆元, 杨平. 形成矩阵的“对号入座”法则与桁段有限元法[J]. 铁道学报, 1986(2): 48−59.

ZENG Qing-yuan, YANG Ping. The “set-in-right- position” rule for formulating dynamic system matrix and the finite element method of truss section for spatial analysis of truss girder[J].Journal of the Chinese Railway Society, 1986(2): 48−59.

[11] 郭向荣, 曾庆元. 高速铁路结合梁桥与列车系统振动分析模型[J]. 华中理工大学学报, 2000, 28(3): 60−62.

GUO Xiang-rong, ZENG Qing-yuan. Analytical model of the system vibration in high speed combination girder bridge and train[J]. Journal of Huazhong University of Science and Technology, 2000, 28(3): 60−62.

[12] 韩艳. 地震作用下高速铁路桥梁的动力响应及行车安全性研究[D]. 北京: 北京交通大学土木建筑工程学院, 2005: 12−56.

HAN Yan. Dynamic responses of high-speed railway bridges and running safety of vehicles during earthquakes[D]. Beijing:Beijing Jiaotong University. School of Civil Engineering, 2005:12−56.

[13] 郑史雄, 奚绍中. 大跨度刚构桥的地震反应分析[J]. 西南交通大学学报, 1997, 32(6): 586−591.

ZHENG Shi-xiong, XI Shao-zhong. Seismic response analysis of long span rigid frame bridges[J]. Journal of Southwest Jiaotong University, 1997, 32(6): 586−591.

[14] 周雍年, 章文波, 于海英. 数字强震仪记录的长周期误差分析[J]. 地震工程与工程振动, 1997, 17(2): 1−9.

ZHOU Yong-nian, ZHANG Wen-bo, YU Hai-ying. Analysis of long-period error for accelerograms recorded by digital seismographs[J]. Earthquake Engineering and Engineering Vibration, 1997, 17(2): 1−9.

(编辑 杨幼平)

Coupled vibration of train-bridge system of steel truss bridge with seismic effect

DENG Zi-ming, GUO Xiang-rong, ZHANG Zhi-yong

(School of Civil Engineering and Architecture, Central South University, Changsha 410075, China)

In order to study the effect of coupling vibration of train-bridge system on earthquake response, using the least squares method to correct and fit the seismic acceleration, the drift phenomenon of displacement time histories caused by the direct integration of acceleration time history was eliminated. In addition, according to the principle of total potential energy with stationary value in elastic system dynamics and the “set in right position” rule for formulating system matrixes, and taking the track irregularities as system’s self-excitation source with the seismic as external excitation, the coupling vibration equation of train-bridge system considering the seismic excitation was built up. Taking a steel truss girder as an example and using the computer simulation method to establish the dynamic model of train-bridge system,the effect of coupling vibration of train-bridge system on earthquake response was researched. The results show that the dynamic response of the bridge depends primarily on the size of the earthquake, the transverse seismic wave has important impact on the transverse dynamic response of vehicles and bridges, the vertical seismic wave has a major impact on the vertical vibration of the vehicle-bridge system but with little effect on the transverse vibration. However,the influence of the vertical seismic wave on the derailment coefficient, the load decrement rate of wheel mass and the vertical acceleration are so significant that the impact of vertical seismic wave in judging the safety of trains must be considered.

steel truss girder; seismic acceleration; drift phenomenon; coupling vibration; finite element model; dynamic response

U448.22

A

1672−7207(2011)01−0184−08

2009−10−23；

2010−01−20

铁道部科技发展计划项目(2009GD029)

邓子铭(1981−)，男，湖南汝城人，博士研究生，从事列车−桥梁耦合振动分析研究；电话：13787417486；E-mail: hut52@163.com