基于多学科设计优化的共轨管设计优化
2011-02-07裴海灵周乃君杨南胡钟林
裴海灵,周乃君,杨南,胡钟林
(1. 中南大学 能源科学与工程学院,湖南 长沙,410083;2. 湖南大学 先进动力总成技术研究中心,湖南 长沙,410205;3. 湖南奔腾动力科技有限公司,湖南 长沙,410205)
基于多学科设计优化的共轨管设计优化
裴海灵1,2,3,周乃君1,杨南1,胡钟林2,3
(1. 中南大学 能源科学与工程学院,湖南 长沙,410083;2. 湖南大学 先进动力总成技术研究中心,湖南 长沙,410205;3. 湖南奔腾动力科技有限公司,湖南 长沙,410205)
基于多学科设计优化方法,以某型高压共轨柴油机匹配的共轨管容积最佳、压力波动最小、质量最小和进油口位置最佳为目标函数建立共轨管多学科设计优化体系,并在充分考虑各学科间耦合作用的基础上,采用模拟退火算法对多学科设计优化模型进行优化求解。研究结果表明:共轨管的容积由原设计值 21.991 cm3减少到21.756 cm3,减小了1.07%;总质量由1.250 kg减少到1.165 kg,减小了6.8%;压力波动幅度由6 MPa降低至5 MPa,降幅为16.7%;优化后共轨管的整体性能得到提高,能够满足高压共轨燃油喷射系统的要求。
高压共轨;柴油机;共轨管;多学科设计优化
柴油机高压共轨燃油喷射技术在减轻环境污染、节约能源及其柴油机智能化等方面有着突出的技术优势,被行业内认为是最具发展前途的柴油机电控技术[1−2]。共轨管是高压共轨燃油喷射系统中储存燃油的装置,同时也是抑制压力波动的容器;因此,对共轨管的优化研究具有重要意义。目前,对共轨管的研究仅限于采用商业软件对共轨内的压力波动进行模拟及仿真分析[3−5],而对其设计优化方面的研究很少。近年来,出现的多学科设计优化(Multidisciplinary design optimization,MDO)方法是一种通过探索并利用工程系统中各学科间相互作用的协调机制来设计复杂系统和子系统的方法[6],其应用已由传统的航空航天领域扩展到一般制造业。在发动机方面,McAllister等[7]在内燃机的优化研究中引入了多学科鲁棒性设计优化方法来评价设计过程中的不确定性;Suh等[8]采用多学科设计优化技术进行发动机动力系统的设计;袁文华等[9]采用自适应粒子群优化算法对高压共轨燃油喷嘴进行了多学科优化,使喷嘴性能得到大幅度提升;刘孟祥[10]对三效催化转化器进行了多学科设计优化;曾庆生等[11]对发动机转子式机油泵进行多学科优化设计。本文作者采用多学科设计优化方法,对共轨管设计中涉及的材料、机械、流体流动、振动等多学科特性进行分析的基础上,建立共轨管多学科设计优化体系,并针对某型发动机匹配的共轨管进行多学科设计优化研究,以便为共轨管设计优化提供新的研究思路。
1 共轨管多学科设计优化方法
1.1 设计变量及目标函数的选取
设计变量是优化模型的基础,是设计最后所需确定的参数。在优化模型建立过程中,设计变量的选取十分重要。对于共轨管,其关键参数有材料、长度、内/外径、进/出油口位置等,通常采用长径比作为其关键参数。在共轨管设计优化过程中,选取最佳共轨容积、最轻质量、最佳进油管位置和最小压力波动作为设计优化的目标函数,这是多目标优化问题。
1.2 最佳共轨容积的确定
为了使喷油器储存足够的高压燃油和平衡压力波动,共轨管的容积应尽可能大;但从快速建立起动油压和快速调节共轨压力以适应发动机工况变化的角度来说,又希望共轨管容积尽量小;因此,共轨管的容积必然存在1个最优值。
通常,标定工况下每循环供油量可以通过下式计算[12]:

式中:Vb为标定工况下每循环1次的喷油量,mm3;Ne为发动机的标定功率,kW;ge为发动机标定功率时的燃油消耗量,g/(kW·h);n为发动机转速,r/min;Z为冲程系数,两冲程时为1,四冲程时为0.5;i为发动机缸数;ρ为燃油密度,kg/m3。
假设燃油温度不变,则共轨管的压力变化为:

式中:∆p为共轨管中的压力变化,MPa;∆V为共轨管中的体积变化,mm3;E为燃油的弹性模量,MPa;Vr为共轨管容积,mm3。
从共轨管中流出的燃油一部分流经喷油器的盛油腔进入燃烧室,此即每循环供油量;另一部分通过回油孔(A孔)回到油箱。假设喷油器的回油量是每循环供油量的γ倍,则从共轨管流出的燃油量是每循环供油量的(γ+1)倍。流入共轨管的燃油量为高压油泵通过出油阀输入共轨管的油量,因此,

式中:Vp为经高压油泵出油阀输入共轨的油量,mm3。
联立式(1)~(3)可以导出共轨管的最佳容积为:
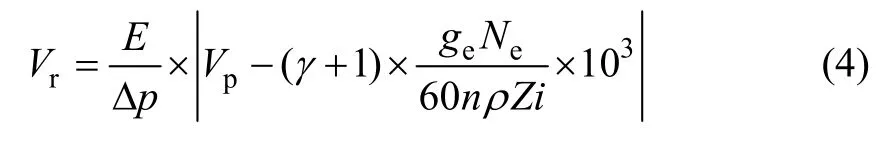
从式(4)可以看出,共轨管的最佳容积不但与发动机的型式参数(缸数、冲程数)、设定参数(功率、燃油消耗率、高压油泵的输出油量及电控喷油器的回油量)有关,而且还与燃油的品质(密度、弹性模量)和发动机的工况等有关。
1.3 约束条件的选取及分析
要保证共轨管工作的安全性,必须要满足材料、流体流动、振动等方面的综合要求,这些要求体现在优化模型中就是要满足一些具体的约束条件。
1.3.1 材料的约束条件
共轨管作为储存和分配高压燃油的部件,对材料必然有一定的要求。首先,承受高达150 MPa甚至更高的压力,需要足够高的强度和刚度;其次,为了减小质量,对材料的密度也有一定的要求;再次,为了尽量避免共轨管的共振影响,应使发动机转速尽量远离共轨管的固有频率。
(1) 材料种类。目前,还未见关于共轨管材料方面的报道。本文在对多种材料进行分析比较后,决定采用42CrMo的合金钢加工共轨管。
(2) 材料强度。共轨管的强度条件为[13]:

式中:a为共轨管内径,mm;b为共轨管外径,mm;p1为共轨内的压力,MPa;p2为共轨外的作用压力,MPa;σ为材料许用应力,MPa。
1.3.2 流体流动的约束条件
来自高压油泵的脉动供油和喷油器周期喷射导致的压力波动,都会沿着油路传回到共轨管中,并依靠共轨管自身的容积对其进行平衡和抑制。关于共轨管内压力波动模型参照文献[14]建立。本文设计要求共轨管中流体的压力变化小于5 MPa。
1.3.3 振动的约束条件
共轨管在工作中主要受到周期激振力、随机激振力和不稳定激振力3种。由于随机激振力和不稳定激振力的随机性和不确定性,本文在共轨管的设计优化中只考虑周期激振力。而共轨管直接安装在发动机缸体上,其受到的振动主要是来自发动机本体。计算零件固有频率的公式为[15]:

式中:fn为固有频率,Hz;K为零件的刚度,N/m;m为零件的质量,kg。
来自高压油泵的压力波动频率fp为[16]:

式中:fp为高压油泵的压力波动频率,Hz;δ为高压油泵的柱塞个数;c为发动机与高压油泵的传动比;k为整数,k=1, 2, 3, …,n。
来自喷油器的压力波动频率fi为[16]:

式中:fi为喷油器的压力波动频率,Hz; 为单循环内喷射次数; 为系数,四冲程时为2,两冲程为1。
本设计中要求发动机转速尽量远离共轨管周期激振频率。
1.3.4 进/出油口的位置
对于共轨管来说,一般都具有(i+1)或(i+2)个进出油口(i为发动机的缸数),其中的1个或2个为进油口,其他为出油口。不同的进油口位置对共轨压力波动及共轨性能是有影响的,因此,寻找最佳的进油口位置对遏制压力波动意义重大。本设计中要求由进油口位置不同引起的压力波动最小。
2 优化模型与算法
2.1 共轨管多学科设计优化模型
综合考虑共轨管的结构、形状参数、材料性能及工作状况等方面的因素,根据MDO设计优化思想,可以建立图1所示的共轨管多学科优化体系。

图1 共轨管MDO体系示意图Fig.1 Schematic diagram of rail tube MDO system
多学科设计问题是一个数学规划问题。因此,共轨管的设计优化问题可描述为:
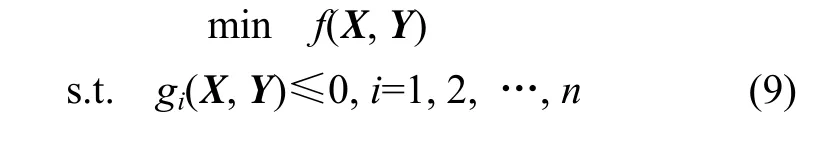
式中:f(X, Y)为目标函数,且f(X, Y)=W1f1(X, Y)/f10(X,Y))+W2f2(X, Y)/f20(X, Y)+W3f3(X, Y)/f30(X, Y) +W4f4(X,Y)/f40(X, Y),f1(X, Y)表示最佳共轨容积目标函数;f2(X,Y)表示压力波动目标函数;f3(X, Y)表示质量目标函数,f4(X, Y)表示进油口位置目标函数,f10(X, Y)表示多学科优化前的共轨容积,f20(X, Y)表示多学科优化前的压力波动;f30(X, Y)表示多学科优化前的质量;f40(X, Y)表示多学科优化前的进油口位置;W1,W2,W3和W4分别表示共轨容积目标函数、压力波动目标函数、质量目标函数和进油口目标函数在总体目标规划中的加权系数,且W1+W2+W3+W4=1;X为设计变量,X=(X1,X2, …,Xn)T,Y=(Y1,Y2, …,Yn)T;gi(X, Y)为约束条件。
该共轨管的多学科设计优化模型采用图2所示过程进行求解。图2中虚线部分为系统分析过程,输入变量为X和Y。X为设计变量,表示共轨管的特征参数;Y为共轨管的参数中固定不变的部分。输出变量为X和Z,Z为状态变量,表示描述共轨管的性能和特征的参数,为所有连接变量组成的向量,也称为连接变量。系统评价的4个学科分析(CA)之间通过连接变量Z相互交换信息(下标表示4学科间关系,如z12表示从学科 1传给学科 2的信息)。系统的整体功能gi则是输入参数X和连接变量Z的函数。最后经过系统总体的评价后得到最优结果。
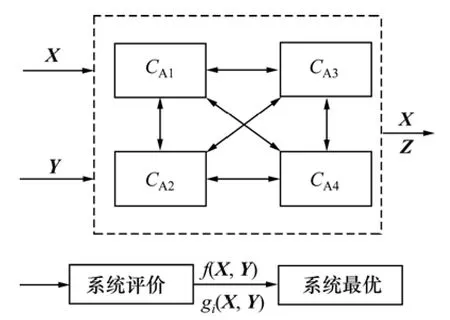
图2 共轨管MDO求解过程示意图Fig.2 Schematic diagram of rail tube MDO solving process
系统分析由4个部分组成,可由以下非线性方程组表示:
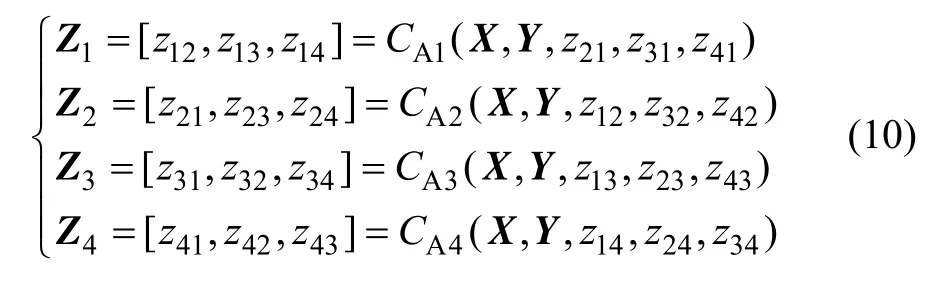
2.2 模拟退火算法
在给定W1,W2,W3和W4的取值范围内,利用模拟退火算法[17−19]对式(9)所示的共轨管多学科设计优化进行求解。
模拟退火算法是用于解决优化问题的一种启发式算法,理论上是一个全局最优算法。其最大的优势在于能够以一定概率跳出局部极值区域从而增大了找到全局极值的概率。
采用模拟退火算法求解共轨管优化问题,将内能E模拟为目标函数f,温度T演化成控制参数X,即可得到寻优问题的模拟退火算法。算法由初始解和控制参数的初始值开始,对当前解重复“产生新解—计算目标函数差—接受或舍弃”的迭代,并逐步衰减控制参数初始值,算法终止时的当前解为所得近似最优解。
3 共轨管多学科设计优化应用
以为某型电控柴油机匹配的共轨管为研究对象,采用图1建立的共轨管多学科设计优化体系对其进行设计优化。表1所示为某型发动机及其配置的共轨管相关参数。

表1 某型电控发动机及其共轨管参数Table 1 Parameters of electronic control engine and rail tube
首先,确定最佳进油口位置。共轨上共有5个进出油口,考虑到其对称性,只考虑第1孔(5孔)、第2孔(4孔)和第3孔(中间孔)3种位置进油的情况,采用文献[14]建立的共轨压力计算模型,对 3种情况下的压力波动进行计算。图3所示为当共轨压力是135 MPa时3种进油位置的压力波动比较情况。从图3可以看出:中间孔进油时的压力波动相对较小且满足小于 5 MPa的要求。因此,本文选择中间孔进油方式。
其次,由表1给出的发动机参数按照式(4)计算得到共轨管的容积应为21.991 cm3,根据不同长径比计算得到对应的共轨外径、长度及调整后的共轨容积,如表2所示。根据发动机机体的尺寸和安装条件,本文选取了第6组数据。按表3所示的约束条件可得到共轨管尺寸,进而得到优化后的共轨管容积。
最后,按照图2所示求解过程采用模拟退火算法对共轨管进行优化。表4所示为共轨管多学科设计优化前后优化目标的相关参数。
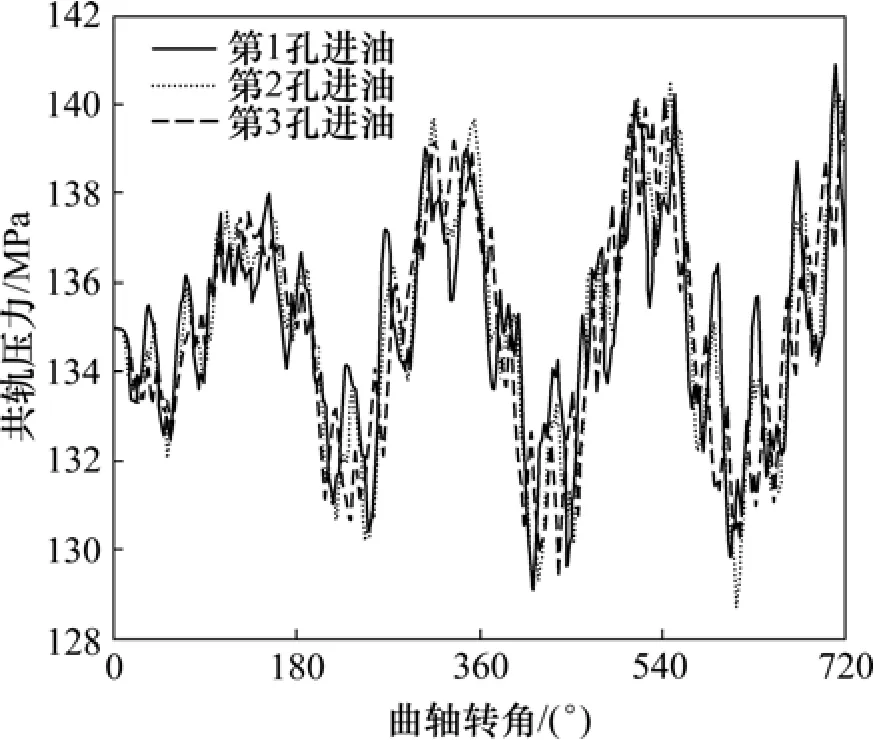
图3 3种进油位置时的共轨压力比较Fig.3 Comparison of rail pressure for three different fuel inlet positions
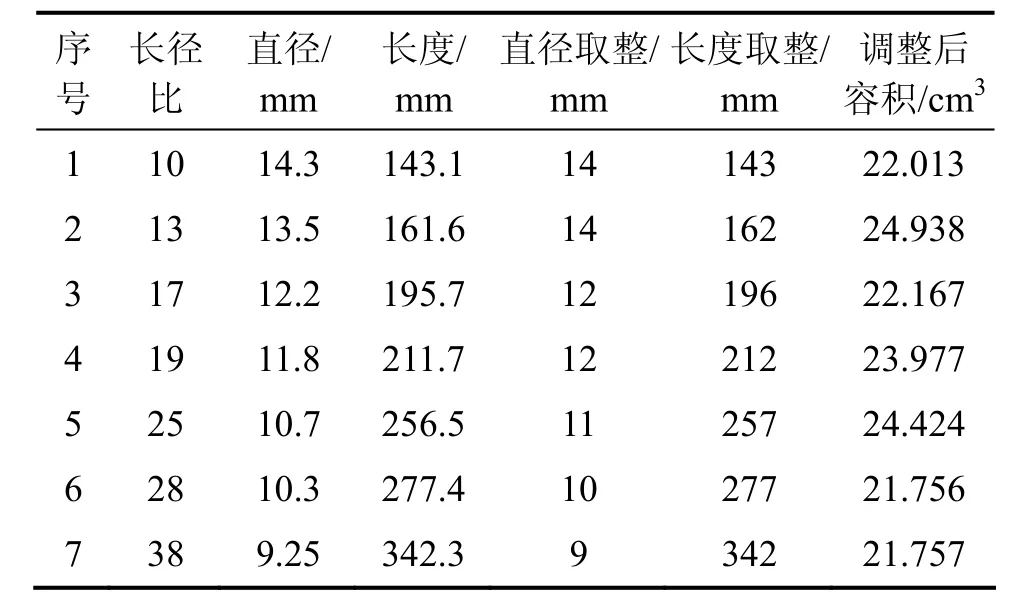
表2 共轨管尺寸Table 2 Parameters of rail tube

表3 MDO约束条件Table 3 Constraint conditions for rail tube MDO
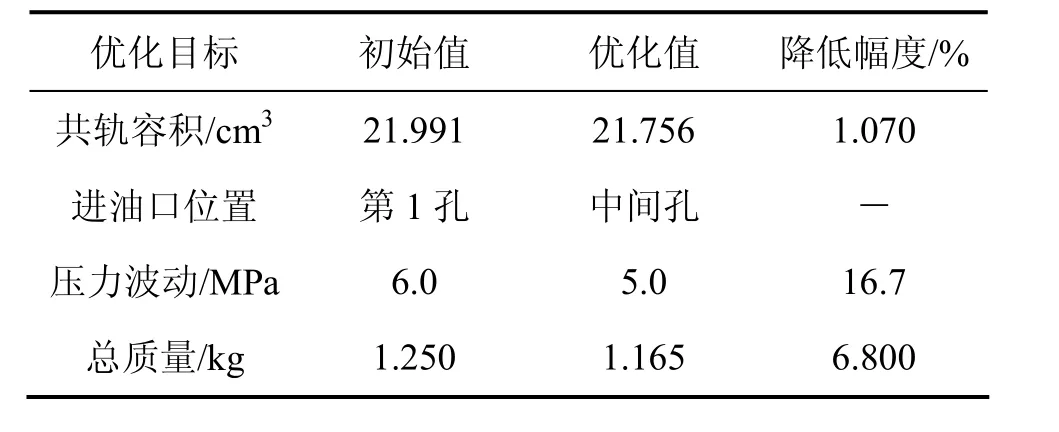
表4 MDO优化目标的相关参数Table 4 Optimization target parameters for rail tube MDO
从表4可以看出:共轨容积、进油口位置、压力波动和共轨总质量均得到了明显优化;其中:共轨管容积由21.991 cm3优化到21.756 cm3,减小了1.07%;进油口位置由第1孔优化到中间孔,压力波动由6 MPa优化到5 MPa,减小了16.7%;总质量由1.250 kg优化到1.165 kg,减小了6.8%。从共轨管的实际运行情况来看,不但使其整体性能得到提高,而且完全满足高压共轨燃油喷射系统的要求,证明所建立的共轨管多学科设计优化体系是行之有效的。
4 结论
(1) 采用多学科设计优化方法进行共轨管的设计。通过充分考虑各学科间的耦合效应,既找到了最优的共轨容积和最佳进油孔位置,又减少了共轨管质量,降低了共轨压力波动,因而为共轨管的设计提供了一种新思路。
(2) 采用模拟退火算法对多学科设计优化模型进行优化求解。共轨管的容积由原设计值21.991 cm3减少到21.756 cm3,减小了1.07%;总质量由1.250 kg减少到1.165 kg,减小了6.8%;压力波动幅度由6 MPa降低至5 MPa,降幅为16.7%。
[1] 王平, 宋希庚, 薛冬新, 等. 高压共轨电控直喷式柴油机喷油规律和放热规律对燃烧噪声的影响[J]. 燃烧科学与技术,2008, 14(5): 406−411.
WANG Ping, SONG Xi-geng, XUE Dong-xin, et al. Effects of fuel injection rate and heat release rate on combustion noise of DI diesel engines[J]. Journal of Combustion Science and Technology, 2008,14(5): 406−411.
[2] 何建辉, 王波涛, 张阿庆, 等. 单缸柴油机高压共轨燃油喷射控制系统的研究[J]. 内燃机工程, 2009, 30(2): 61−64.
HE Jian-hui, WANG Bo-tao, ZHANG A-qing, et al.Development of control system for high pressure common rail injection system in single-cylinder engine[J]. Chinese Internal Combustion Engine Engineering, 2009, 30(2): 61−64.
[3] 王军, 张幽彤, 林秀霞. 军用柴油机高压共轨系统共轨管设计与仿真[J]. 装甲兵工程学院学报, 2008, 22(3): 43−46.
WANG Jun, ZHANG You-tong, LIN Xiu-xia. Design and simulation on common rail line of high pressure common rail injection system in military diesel engine[J]. Journal of Academy of Armored Force Engineering, 2008, 22(3): 43−46.
[4] 于建国, 梁超. 变容变压条件下电控柴油机共轨管长径比对压力波动的影响[J]. 车辆与动力技术, 2008(2): 26−30.
YU Jian-guo, LIANG Chao. Under the conditions of modulation pressure & volume the length-diameter ratios of common rail electronic control diesel engine impact on pressure fluctuation[J].Vehicle & Power Technology, 2008(2): 26−30.
[5] 王立强, 刘铭, 李晓波, 等. 柴油机共轨管与高压油管结构参数对系统的影响[J]. 应用科技, 2005, 32(4): 51−53.
WANG Li-qiang, LIU-ming, LI Xiao-bo, et al. Influence of change of common-rail and high-pressure fuel pipe parameters in electric control system of diesel engine on system performance[J]. Applied Science and Technology, 2005, 32(4):51−53.
[6] 李响, 李为吉. 飞行器多学科设计优化的三种基本类型及协同设计方法[J]. 宇航学报, 2005, 26(6): 693−697.
LI Xiang, LI Wei-ji. Three kinds of basic multidisciplinary optimization problems in flight vehicle design and application of collaborative optimization[J]. Journal of Astronautics, 2005,26(6): 693−697.
[7] McAllister C D, Simpson T W. Multidisciplinary robust design optimization of an internal combustion engine[J]. Journal of Mechanical Design, 2003, 125(1): 124−130.
[8] Suh M W, Shim M B, Kim M S. Multidisciplinary design optimization of engine mounts with consideration of the driveline[J]. Journal of Automobile Engineering. 2003, 217(2):107−114.
[9] 袁文华, 鄂加强, 龚金科, 等. 自适应粒子群优化的高压共轨燃油喷嘴多学科优化设计[J]. 内燃机工程, 2009, 30(5): 63−67.
YUAN Wen-hua, E Jia-qiang, GONG Jin-ke, et al.Multidisciplinary design optimization for fuel nozzle of high pressure common-rail injection system based on self-adaptive particle swarm optimization algorithm[J]. Chinese Internal Combustion Engine Engineering, 2009, 30(5): 63−67.
[10] 刘孟祥. 三效催化转化器高效长寿低排放优化设计理论及方法研究[J]. 长沙: 湖南大学机械与运载工程学院, 2008:86−97.
LIU Meng-xiang. The research on the highly efficient, longevous and low-emission optimization design theory and method in three-way catalytic converter[D]. Changsha: Hunan University.College of Mechanical and Vehicle Engineering, 2008: 86−97.
[11] 曾庆生, 杨毅, 王湘江. 转子式机油泵多学科优化设计[J]. 内燃机工程, 2009, 30(5): 73−77.
ZENG Qing-sheng, YANG Yi, WANG Xiang-jiang.Multidisciplinary optimization design on rotor oil pump[J].Chinese Internal Combustion Engine Engineering, 2009, 30(5):73−77.
[12] 李正帅. 高压共轨式电控燃油喷射系统的计算机仿真[D]. 西安: 西安建筑科技大学机电工程学院, 2001: 26−27.
LI Zheng-shuai. Computer simulation of high pressure common rail fuel injection system electronically controlled[D]. Xi’an:Xi’an University of Architecture and Technology. School of Mechanic and Electronic Engineering, 2001: 26−27.
[13] 殷尔禧. 材料力学[M]. 北京: 科学技术文献出版社, 1994:588−590.
YIN Er-xi. Material mechanics[M]. Beijing: the Science and Technology Press, 1994: 588−590.
[14] 虞金霞, 郭海涛, 卓斌. 共轨式喷油系统数学模型[J]. 上海海运学院学报, 2002, 23(2): 30−34.
YU Jin-xia, GUO Hai-tao, ZHUO-bin. Mathematic model of common rail fuel injection system[J]. Journal of Shanghai Maritime University, 2002, 23(2): 30−34.
[15] 钱桦, 安静贤. 65Mn 钢的固有频率与热处理的实验研究[J].北京林业大学学报, 1998, 20(5): 52−54.
QIAN-hua, AN Jing-xian. Natural frequency of 65Mn steel and heat treatment[J]. Journal of Beijing Forestry University, 1998,20(5): 52−54.
[16] Kristina A. Modeling of pressure waves in the common rail diesel injection system[D]. Linkopings: Linkopings University.Department of Electrical Engineering, 2000: 12−17.
[17] 邹恩, 李祥飞, 刘耦耕. 最优模糊神经网络参数的设计: 混沌模拟退火学习法[J]. 中南工业大学学报: 自然科学版, 2004,35(3): 443−447.
ZOU-en, LI Xiang-fei, LIU Ou-geng, et al. Optimization design for parameters of FNN: Learning algorithm of chaos simulated annealing[J]. Journal of Central South University of Technology:Natural Science, 2004, 35(3): 443−447.
[18] 刘洪普, 侯向丹. 模拟退火算法中关键参数的研究[J]. 计算机工程与科学, 2008, 30(10): 55−57.
LIU Hong-pu, HOU Xiang-dan. Research on the key parameters in the simulated annealing algorithm[J]. Computer Engineering& Science, 2008, 30(10): 55−57.
[19] 王知人, 张胤, 李新乔. 一种改进的模拟退火算法[J]. 高等学校计算数学学报, 2006, 28(1): 15−19.
WANG Zhi-ren, ZHANG Yin, LI Xin-qiao. A kind of renewed simulated annealing algorithm[J]. Numerical Mathematics: A Journal of Chinese Universities, 2006, 28(1): 15−19.
(编辑 赵俊)
Rail tube optimization based on multidisciplinary design optimization
PEI Hai-ling1,2,3, ZHOU Nai-jun1, YANG Nan1, HU Zhong-lin2,3
(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;2. Research Center for Advanced Power-train Technology, Hunan University, Changsha 410205, China;3. Peteco Company Ltd, Changsha 410205, China)
Based on multidisciplinary design optimization (MDO) method,the rail tube MDO system was established using the optimal volume, least pressure oscillation, the smallest mass and the best inlet position as the objective functions. Taking the multidisciplinary coupling effect into full consideration, the MDO system was solved by the simulated annealing algorithm. The results show that the rail volume is decreased from 21.991 cm3to 21.756 cm3, with 1.07% reduction ratio;the mass of rail tube is reduced from 1.250 kg to 1.165 kg, decreased by 6.8%. And the pressure fluctuation of the rail tube is dropped from 6 MPa to 5 MPa, with 16.7% fall. The global performance of the rail tube is improved largely.
high pressure common rail; diesel engine; rail tube; multidisciplinary design optimization
TK422
A
1672−7207(2011)01−0234−06
2010−03−11;
2010−06−20
国家“863”计划项目(2008AA11A116)
裴海灵(1979−),男,山西太原人,博士,从事柴油机高压共轨燃油喷射系统研究;电话:13487493751;E-mail: peihailing@yahoo.com.cn
