一道2010年中考题的教学分析

●罗增儒 (陕西师范大学数学系 陕西西安 710062)

一道2010年中考题的教学分析

●罗增儒 (陕西师范大学数学系 陕西西安 710062)

这是一道对初中生来说难度很大的问题．据测试，大约300人中只有9人做对，初中教师做对的概率也很低(有人怀疑超纲)．本文想以此作为解题教学的示例，分4个步骤讲解如下．

题目水管的外部需要包扎，包扎时用带子缠绕在管道的外部．若要使带子全部包住管道且不重叠(不考虑管道2端的情况)，需计算带子的缠绕角度α(α指缠绕中将部分带子拉成图1所示的平面ABCD时的∠ABC，其中AB为管道侧面母线的一部分)．若带子宽度为1，水管直径为2，则 α的余弦值为 ＿＿．

图1

(2010年浙江省绍兴市数学中考试题)

1 理解题意

包括3项基本工作:

(1)条件是什么?一共有几个?其数学含义如何?

条件有4个:

①以水管及附图为载体给出一个圆柱，从而圆柱的所有性质可视为已知．

②圆柱(水管)的底面直径为2，从而底面及水平截面圆的周长、面积等可视为已知．

③以带子缠绕管道为载体给出圆柱侧面的一个斜长条图形覆盖，斜长条图形展平时底边与母线的夹角为α．

④带子宽度为1，即2条平行线间的距离为1．但带子宽度应在什么地方出现呢?文中没有明确的交待．

(2)结论是什么?一共有几个?其数学含义如何?

结论有1个:求角α的余弦值．

(3)条件与结论有什么初步联系?

①结论所需要的直角三角形应该在条件③的斜长条图形的展开图中．而为了得出展开图，需要用到条件①中圆柱的性质，结合本例有:

1°圆柱的母线与底面垂直;

2°圆柱侧面沿母线剪开的展开图为矩形，而不沿母线剪开的展开图可以为平行四边形．

②为了找出结论所需要的直角三角形，从条件①和条件④中找出提供直角的2处机会:

1°“圆柱的母线垂直于底面”;

2°“带子宽度为1”，即2条平行线间的距离，有垂直的含义．

③为了找出计算余弦值所需要的“邻边、斜边”，我们关注条件②和④．由底面直径为2知，圆柱的底面周长为2π;由带子宽度为1知，点A到BC的距离为1．

条件与结论的更深入联系由“思路探求”阶段去完成．

2 思路探求

(1)为了求角α的余弦值，要寻找α所在的直角三角形．

(2)为了找直角三角形，把缠绕一圈的带子展开，这时出现一个平行四边形和角α，但还没有出现直角三角形(参见图2中的实线)．

(3)为了出现直角三角形，连结AC，并作AH⊥BC，有 AC=2π，AH=1，AB⊥AC(如图 2)，得出 3个直角三角形:Rt△BAC，Rt△ABH，Rt△AHC(可以不用)．

(4)由于Rt△AHC有2条已知边，因此每个锐角的余弦都可求得．由同角的余角相等知，∠CAH=∠B=α(解法见文献［1］)．

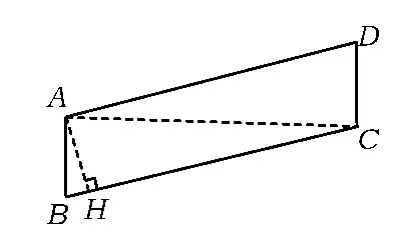
图2

3 书写解法

解设图1中带子的一圈里，点 C与点 A重合、CD与AB共线，则缠绕一圈的带子展开后为平行四边形(如图2)，作对角线AC及边上的高AH，则AC⊥AB．由△ABC≌△HAC，得

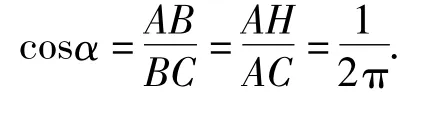
4 反思回顾

(1)问题解决的关键是将图1中缠绕一圈的带子展开(如图2)，把空间问题化归为平面几何中解直角三角形的问题求解．主要有以下3个化归:

化归1把一个实际问题转化为一个数学问题(需要空间想象能力);

化归2把一个空间数学问题转化为平面数学问题(平行四边形)(需要构造性思维能力);

化归3把一个平面数学问题转化为解直角三角形．

(2)用到的数学知识有:

①圆柱．圆柱母线垂直于底面，圆柱侧面展开图为矩形．

②平行四边形的判定．当把缠绕一圈的带子展开时(空间图形向平面图形转化)，AD平行并等于BC，因而四边形ABCD是平行四边形．但是这个四边形上鲜有已知条件．

③直角三角形相似．作辅助线AC，AH，把平行四边形的内角转化为直角三角形的内角，并且出现了条件②和条件④，有△ABC≌△HAC(可用“同角的余角相等”来代替)．

④余弦的定义．

(3)主要困难有:

①在把一个实际问题转化为一个数学问题时，想象不出带子是如何缠绕在管道外部的，弄不清应该转化为一个什么样的数学问题，因而很多学生读完题目后便不知如何入手了．

解决办法:可动手操作，转化为平行四边形的内角问题．

②把一个空间数学问题转化为平面数学问题时，将带子展开为平面图形具有开放性，学生想象不出展开图形是什么，因而原图1中的曲线BC不知该拉直到什么地方，这样就找不到角α．

③有一部分学生把笔作为水管、用纸条进行操作(这是好办法)，但会误认为一周的展开图是矩形(把 α 作为90°)．

解决办法是通过正确操作，把图1中的CD还原为与AB共线．

④想不到母线与过点A的圆周展开线垂直，因而“水管直径为2”的条件没有用上，辅助线AC也出不来．即使辅助线AC出来了，也不知道△ABC为直角三角形．

解决办法:可以过点A作一个截面圆．

⑤误认带子宽度为AB，从而AB=1，带子宽度的辅助线AH出不来．

⑥很多学生得出数值大于1的答案，这说明对余弦值概念理解不透．也反映出教师或学生对课本中“探究活动”重视得不够．

本例的更多分析请参见文献［1］．

［1］ 王春丽．一题一世界 亮点成永恒——绍兴卷第16题［J］．中学数学教学参考(中旬)，2010(9):60．