简论学生数学编题策略
2011-02-02牟素珍城北中学浙江乐清325600吴立建乐清市教研室浙江乐清325600
●牟素珍 (城北中学 浙江乐清 325600) ●吴立建 (乐清市教研室 浙江乐清 325600)
简论学生数学编题策略
●牟素珍 (城北中学 浙江乐清 325600) ●吴立建 (乐清市教研室 浙江乐清 325600)
学生编题到目前为止还没有明确和统一的定义,仁者见仁、智者见智.笔者认为学生编题是根据自己对所学知识的理解,在给出某个数学对象的基础上,进行再加工、再创造后,编拟出新的数学问题.学生编题的过程是从一个简单的问题出发,逐步演绎深化、探究创新的过程.让学生编题不仅可以加深学生对所学知识的理解,而且有助于培养思维的独立性和创造性;对防止题海战术,提高课堂效率也大有裨益.因此,笔者结合自己的所教、所感谈谈学生数学编题策略,供参考.
1 拟制题
拟制题一般以原有题为基础,对其进行一定变形后成为另一形式的题,俗称为改编题.这样可以通过对典型题进行适当的剖析、深入研究、充分演变,揭示其深刻性,领悟其奥妙性.
1.1改变问题的条件
改变问题的条件,就是对某一个问题的条件进行变化探讨,并针对问题的内涵与外延进行深入与扩展,得到一类变式题组.通过对问题的分析解决,掌握某类问题的题型结构,深入认识问题的本质,有利于培养学生思维的连动性和变通性.
例1如图1,一只蚂蚁从棱长为2的正方体的顶点A爬到与它相距最远的另一个顶点G,则蚂蚁爬行的最短路程是多少?
变化1如图2,一只蚂蚁从长为3、宽为1、高为2的长方体顶点A爬到与它相距最远的另一个顶点G,则蚂蚁爬行的最短路程是多少?
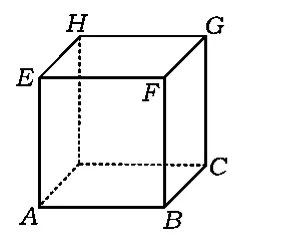
图1
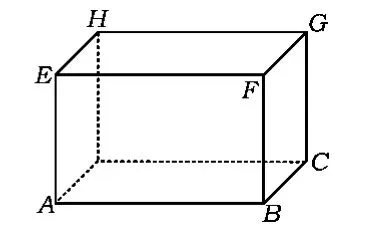
图2
变化2如图3,圆锥底面半径为1,母线长为3,一只蚂蚁从底面圆周上的点B出发,沿圆锥侧面爬行到圆锥AB的轴截面上的另一母线AC的中点D,问蚂蚁沿怎样的路线爬行,可使路程最短,最短路程是多少?
(浙教版九年级上册93页练习题)
变化3如图4,蚂蚁从圆柱母线AB的端点A沿着圆锥侧面爬到点B,若圆柱底面半径为1,高为3,则蚂蚁爬行的最短路程是多少?
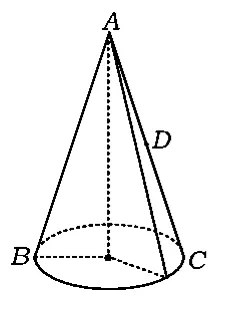
图3
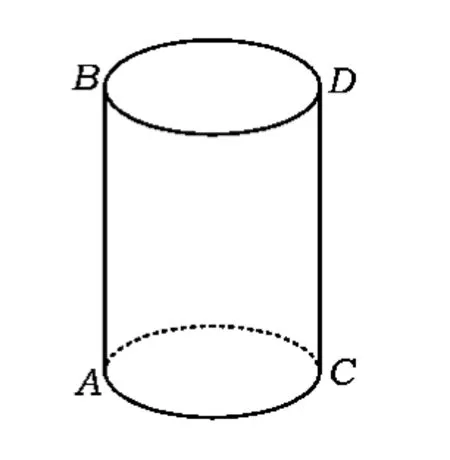
图4
编题意图此题将引例中的正方形演变为长方形、圆锥、圆柱,通过对蚂蚁爬行的最短路程的求解,掌握立体图形上两点之间最短距离的求法.就是把立体图形展开,转化为平面图形,再利用两点之间线段最短去求解.
在拟制时,可以尝试把问题条件中的图形进行转化,可将特殊图形向普通图形进行转化;特殊图形(如特殊的三角形)之间进行相互转化;三角形的角平分线向高线、中线转化;看是否还存在某些相同的方法或结论.也可对条件中的数量关系进行改变.
1.2 改变问题的设问方向
改变问题的设问方向,就是针对综合性较强的数学问题,引导学生将其分解为几个基本问题,通过对基本问题的求解,逐步达到解决问题的目的.当一个问题获得解决后,启发探索问题解决后产生的一系列更深刻的数学问题,从而培养学生思维的广阔性和深刻性.例如在初三专题复习时拟制了如下题目:
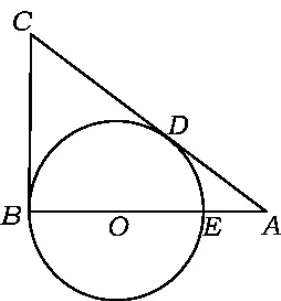
图5
例2已知在△ABC中,∠B=90°,O 是 BA上的一点,以点O为圆心,OB为半径的圆与BA交于点 E,与 AC切于点 D,AD=2,BE=3,如图 5.设 P 是线段BA上的动点(点 P与点 A,B不重合),BP=x.
(1)求AE的长;
(2)当x为何值时,以P,A,D为顶点的三角形是等腰三角形?
变化1当x为何值时,以P,A,D为顶点的三角形与△ABC相似?
变化2当x为何值时,PD+PC的和最小?
变化3当点P运动时,四边形PBCD的面积与x有何关系?
编题意图把知识点进行整合与渗透,让学生学会综合运用所学的知识与技巧,去解决有关问题.并掌握解决动态几何型问题的策略:化动为静——利用运动中特殊点的位置将图形分类;静中求动——针对各类图形,分别解决动态问题.
改变习题的设问方向,进行多角度、多方位、多层次的讨论和思考,使知识点融会贯通,从而建立起高效、合理的知识结构,更好地培养学生综合运用知识解决问题的能力.
1.3 变静态为动态
变静态为动态,就是以基本图形为“基准点”,通过基本图形的运动,将一个问题转换成更一般的问题,把所研究的图形扩展到更大范围内进行考查,开阔解决问题的视野,培养举一反三、触类旁通的思维品质和创新精神.以浙教版八年级上册第27页练习2为例:
如图6,在等腰△ABC中,AB=AC,点D为BC的中点,则点D到AB和AC的距离相等.请说明理由.
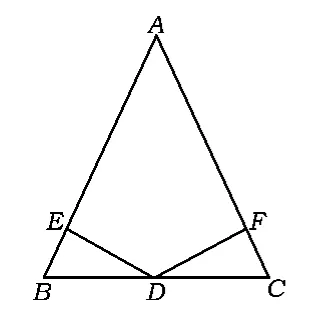
图6
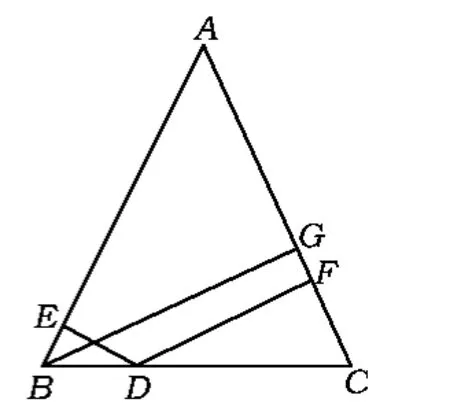
图7
变化1如图7,在等腰△ABC中,AB=AC,点D为BC的一个动点(中点除外),则点D到AB和AC的距离相等吗?当点D运动到与点B或点C重合时,你发现了什么?
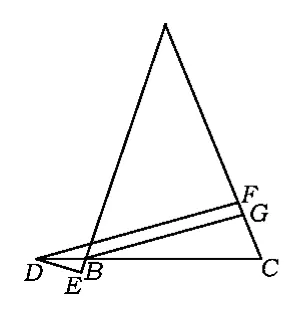
图8
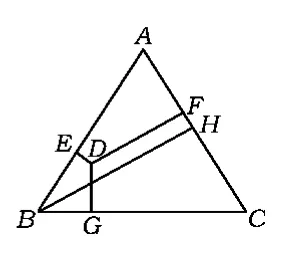
图9
如果让点D运动到CB的延长线上(如图8),结果如何?再进一步,若点D是正三角形内(如图9)或外(如图10)的一点,关于高线之间又有怎样的数量关系?
编题意图不断的变换问题的条件和结论,让学生学会用“同一图形的面积相等,表示方法不同”证明一类含有线段的等式,揭示问题的实质与条件、结论之间的内在联系.
由于运动而导致图形的形状发生变化,从而导致数量关系的变化,而这种数量关系恰好就是问题所研究的.通过探究问题实质的变与不变,学会从“变”的现象中发现“不变”的本质,从“不变”的本质中探究“变”的规律.
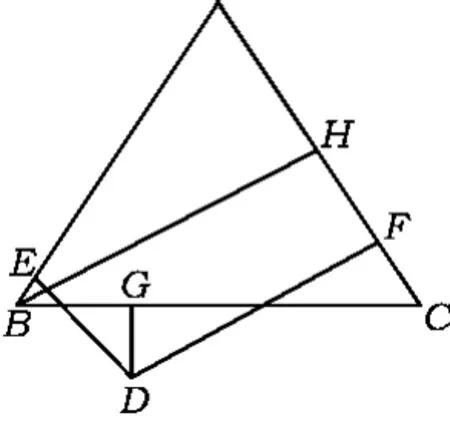
图10
1.4 从具体到一般
从具体到一般就是将原问题的条件在元素的数量上或几何纬度上进行推广以寻求更普遍的规律;几何中常表现为线段或边数、角度的增加;代数中常表现为变量个数的递增、常量向变量的转换,从而培养学生的变换能力及思维的灵活性和多向性.以浙教版教科书七年级上册第156页练习3(1)为例:
在图11中有几条线段?把它们都写出来.
变化1如图12,在直线a上取n个不同的点,那么直线a上一共有多少条线段?
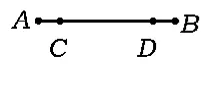
图11
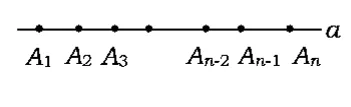
图12
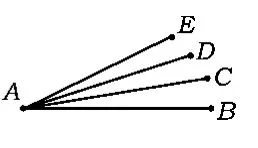
图13
变化2如图13,若变成角,则图中一共有多少个锐角?
变化3平面内n个不同的点中任意3个点都不在同一条直线上,那么过其中每2个点画直线,一共可以画出几条直线?
变化4一次聚会出席的每位代表都和其他代表各握过一次手,统计结果表明,一共握手45次,问参加聚会的代表有多少人?
(浙教版教科书八年级下册第33页练习5)
编题意图在解决复杂的计数问题时,应寻找其特有的规律,这样才能做到不重不漏.从本题可以看出,有时记住一些常见且有用的知识结论,可以迅速、有效的联系问题中的未知与已知,从而达到解题的目的.
在找规律过程中,会涉及到一个或者几个变化的量,通常按照一定的顺序给出,且包含事物的序列号,要善于总结、发现规律,并按规律去解题.相近、相似的同类数学题可从中领略多题一解、异形同解的妙趣.
2 编制题
编制题就是学生根据自己的体验结合数学知识创造出新的练习题,一般要对原问题进行抽象加工,俗称原创题.学生除了要具备相应的数学知识外,还要具备一定的生活常识、想像力及创造力.
2.1 编制基础知识题
新知识点若不经过及时的复习、反思,则很容易遗忘.数学复习从梳理基础知识入手,通过对所学的知识进行加工、整理,并纳入相应的“知识库”,使之结构化、系统化,形成“知识网络”.这样,运用时可准确、迅捷地从“知识库”中提取有效的知识信息解决问题,进而掌握《课程标准》中应掌握的知识,形成《课程标准》中应形成的能力.例如在复习“等腰三角形的性质”时,可这样编制:
问题1已知在△ABC中,AB=AC,你可得出什么结论?
问题2在△ABC中,AB=AC=13,BC=10,你能求出△ABC的面积吗?
问题3如图14,在△ABC中,AB=AC,点M为BC的中点MH⊥AB于点H,ME⊥AC于点E则MH=ME?如果点M为BC上的动点,那么结论还成立吗?,,
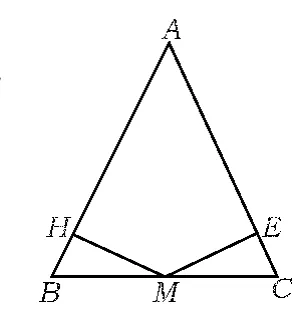
图14
问题4在△ABC中,AB=AC,点E在AC上,D是BA延长线上一点,且AD=AE,DE的延长线交BC于点F,则DF⊥BC吗?
编题意图进一步理解和掌握等腰三角形的知识要点,学会灵活运用所学知识解决问题.在解题过程中,不断学习和积累解题经验,提高分析问题、解决问题的能力.
对于编制基础知识题,学生应先对照教材把知识点系统地梳理一遍,然后根据重点、难点,设计有层次、有梯度、题型多变的练习题,完善知识结构、梳理知识网络,提高自主学习的能力.
2.2 编制实际应用题
对于编制实际应用题,一般是用一段文字描述一个与自己生活经验贴近的故事或事件.它需要学生学会用数学的眼光观察世界、用数学的思维思考世界、用数学的方法了解世界,逐步学会“做数学”和“数学地思考”.
2.2.1 将生活问题数学化
将生活问题数学化,就是学生运用所学的知识解决日常生活中的数学问题.它需要学生用数学的眼光去观察周围的生活现象,思考能否用数学的知识、方法、观点和思想去解决所遇到的问题,体会数学的应用价值.笔者在初三总复习讲解“如何解决实际问题”时,曾给出2个数据让学生尝试编题:
教师看见一家商店广告上醒目地写着大削价:大杯10元/只,小杯8元/只.现在请你添加合理的情境和数据,使之成为一个完整的实际问题,并能运用所学的知识解决.
在教学过程中,把学生编制的以下问题作为研究对象:
(1)王老师买了13只杯子作为运动会的奖品.已知大杯10元/只,小杯8元/只,共花了114元.请问:王老师买了大杯、小杯各几只?
(2)小明“五一”节去超市买杯子,其中大杯10元/只,小杯8元/只,付了30元找回2元,问小明买了几个杯子?
(3)冰冰准备在家举办生日晚会.她去买杯子,大杯10元/只,小杯8元/只.总共买15只杯子.如何买才能使总价格不超过120元?
(4)某商店水杯的进价为4元/只,售价为10元/只,每天可卖100只.经市场调查,每降价1元,每天可多售出20只,问单价为多少元时,每天获利最大?
从学生熟悉的生活情景出发,选择学生身边感兴趣的事物,提出有关的数学问题,以激发学生的兴趣与动机,使学生初步感受数学与日常生活的密切联系.
2.2.2 将数学问题生活化
现实生活是数学的丰富源泉,只要细心观察就不难发现,生活中到处都有数学知识.我们可以把所学的数学知识应用到生活中去,并体验数学来源于生活又服务于生活的乐趣.例如在复习“圆的基本性质”时可这样编题:
2011年3月11日,日本气象厅表示,当地时间14时46分,日本东北部海域发生里氏8.9级地震并引发海啸,造成重大人员伤亡和财产损失.
问题1受11日大地震的影响,日本东京电力公司福岛第一核电站3号机组当地时间14日上午11点过后发生氢气爆炸.在爆炸中某排污管道井盖炸裂(如图15),你能尽快找出圆心的位置吗?
问题2如图14,经过测量得井盖的直径为2 m,在福岛电站工作人员的抢修下,井盖在当天下午3点修复好.安装时发现污水正快速流出,此时的液面宽度刚好为1.5 m(如图16),请你求出污水的最大深度.

图15
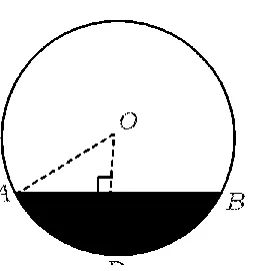
图16
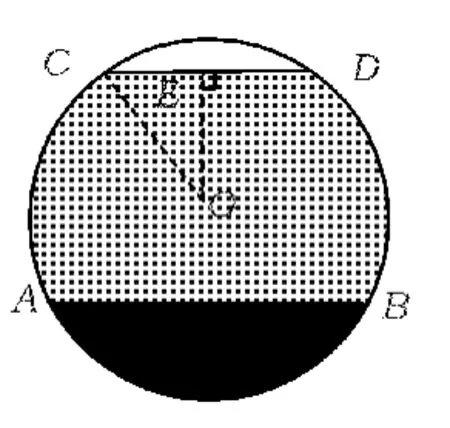
图17
问题3半小时后,井盖装好.晚上7时工作人员通过电脑显示发现污水管液面已恢复到正常深度水位1.6 m(如图17),你能求出此时液面CD的宽吗?
在现实世界中,我们要开阔视野、拓展思维,认真地钻研教材,用生活中的事情呈现教学内容,创设生活情境,体验数学知识与日常生活的密切联系.
以上编题的方法在实际运用中可以互相结合、灵活运用.在编题时,要目的明确、表述清楚、准确无误、设问可解.在此基础上,尽量突出习题的应用性、层次性、开放性.通过编题,让学生在无穷的变化中领略数学的魅力,在曼妙的演变中体会数学的快乐,自觉地学习和感悟数学,从而促进有效建构.
[1] 王伟.数学变式百例精讲[M].宁波:宁波出版社,2006.
[2] 徐卫东.变式习题 变换思维[J].中学数学教育,2009(7-8):63-65.
[3] 王明山.题的理解进展探究[J].数学通报,2011(1):42-45.
