机织复合材料双球型冲压的有限元模拟

Zia-U r-Rehman 彭雄奇 石少卿 丁纺纺

1.西北工业大学,西安,710072 2.上海交通大学,上海,200030 3.后勤工程学院,重庆,401311

机织复合材料双球型冲压的有限元模拟

Zia-U r-Rehman1彭雄奇2石少卿3丁纺纺1

1.西北工业大学,西安,710072 2.上海交通大学,上海,200030 3.后勤工程学院,重庆,401311

利用基于连续介质力学的有限元法对机织复合材料织物的冲压过程进行了模拟仿真。一个非正交本构模型被用来描述机织复合材料在大变形下由于经纱和纬纱之间角度变化所引起的非线性各向异性材料行为。利用双球形基准冲压模拟装置对平纹机织复合材料进行常温下的冲压成形模拟仿真,编写了ABAQUS/Standard中的用户材料子程序来描述机织复合材料的材料属性。模拟结果与实验结果对比表明,机织复合材料冲压成形模拟分析结果与实验结果具有良好的一致性。

机织复合材料;有限元分析;成形模拟;双球型模具;非正交本构模型

0 引言

机织复合材料以其高比强度、高比模量和低成本的结构优势而越来越广泛地运用于航空和汽车制造业。由于纤维束在纤维方向上的拉伸和沿对角线方向上的大量伸长而使机织复合材料具有良好的稳定性和可成形性,这些特征使得机织复合材料可以被加工成较复杂的形状。通过数值模拟可以对机织复合材料冲压成形进行分析和工艺优化设计。

机织复合材料成形模拟较为常见的途径为几何学方法和连续介质有限元法。几何学方法以运动学为基础[1-2],其模型相对比较简单且运算量不大。然而,这些模型由于不考虑机织复合材料各组成部分的力学属性和边界条件而存在很大的缺陷,它们不能提供应变和应力分布,而这些信息对成形极限分析和工艺优化设计至关重要。相对而言,连续介质方法则把机织复合材料看成是各向异性的连续统一体并把纤维本构模型的力学属性考虑在内[3-5]。此外,连续介质方法还可以处理复杂的边界和变形条件。该方法的主要优势就在于它能应用到有限元方法中。Khan等[6]以追踪成形过程中纤维再定位的旋转张量为基础发展了一种机织复合材料的超弹性模型,他们的双球形冲压模拟结果与实验结果具有良好的一致性。ten Thije等[7]为薄板复合物的成形模拟发展了一种多层三角形膜单元,由于膜单元缺少弯曲刚度从而导致了它并不适合真正的褶皱模拟分析。Lin等[8]发展了一种有限元模型并预测了机织复合材料剪切力和剪切角度之间的关系,该模型强调了边界条件,可以准确地预测大变形条件下的剪切应力。

依据文献[9]中的双球形冲压实验设置,本文建立了相应的有限元模型对平纹机织复合材料进行双球形冲压模拟分析。笔者之前建立的非正交材料模型[5]以用户材料子程序的形式应用到机织复合材料有限元模型中。将机织复合材料变形后的边界轮廓、缩进量和剪切角的模拟结果与双球形冲压的实验结果[6]进行了对比。

1 机织复合材料板材非正交本构模型

如图1所示,用一组标准正交基e i或者一组任意的矢量基gi来表示应力、应变和本构张量。在欧氏向量空间里g i可以当作一个协变基(covariant basis)。两组基之间的关系可定义为[5]

gi的对偶基(recip rocal basis)表示为g(i),它们在欧氏向量空间里是一组逆变基[10](contravariant basis)。

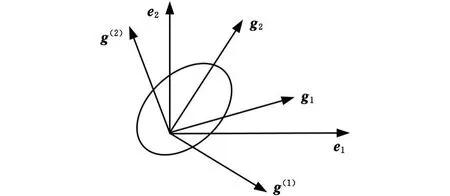
图1 非正交模型的坐标系

一个质点的应变张量ε在逆变坐标系g(i)中的协变分量ij可由笛卡尔坐标系中的εij转化而来:

选择g1、g2与机织物当前的经纬纱线方向一致,如图2所示。为简便起见,g1、g2选为单位向量。g i就构成了反映纤维束再定位的牵连坐标系。

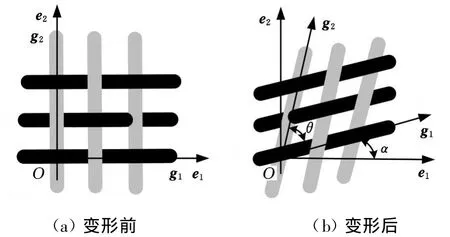
图2 机织复合材料的结构变形示意图

实验研究表明在机织复合材料中可以把剪切应力与正应力进行解耦[11]。因此,逆变弹性矩阵可以假设为具有正交形式,它把牵连坐标系中的逆变应力与协变应变联系了起来:

把式(6)、式(7)代入式(8)可得

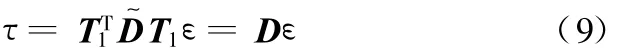
以平纹机织热塑性复合材料(玻璃纤维和聚丙烯树脂)为例进行说明。该复合材料织物的几何参数和各本构相位材料特性见文献[12]。利用之前笔者已经建立的本构模型[5],可以在单个壳单元上进行模拟从而得到壳单元相应的材料性质。拉伸模量(MPa)通过单向拉伸试验获得[5]:

纱线抗压模量设置为0.1MPa。此外,参数化研究表明,泊松比对机织复合材料力学行为的影响可以忽略不计。为简便起见,设定泊松比为0.1。

通过剪切框架(picture-frame)试验可以得到机织复合材料的剪切模量(MPa)如下[5]:

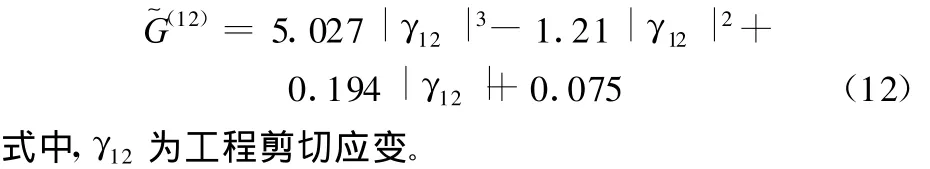
由此可以确定式(8)中逆变弹性矩阵D～中的所有弹性常数。联合式(10),可以在ABAQUS/Standard中为壳单元类型设计一个用户材料子程序用以描述机织复合材料在复杂载荷和变形条件下的各向异性材料行为。

2 平纹机织复合材料的双球形冲压模拟

2.1 冲压模拟装置

依据文献[9],建立了图3所示的双球形冲压仿真模型。将冲头、压板及冲模设置成刚体,其尺寸见文献[9]。机织复合材料有限元模型单元类型采用ABAQUS/Standard中壳单元S4R,其材料属性则通过用户材料子程序来定义。

为了与实验条件一致,把压板力设定为常数值100N,机织复合材料与冲压装置间的摩擦因数定为0.2,冲头位移为60mm。矩形平纹机织复合材料的尺寸与实验[6]中的一致,为 470mm×270mm,厚度为0.78mm。考虑到结构的对称性,采用整体的1/4模型进行有限元模拟,并施加了相应的对称约束。利用ABAQUS进行双球形冲压模拟分析,并将模拟结果与实验结果[6]进行比较。

图3 双球形冲压装置

2.2 结果对比与分析

图4为实验与模拟分析的变形轮廓对比图。可以看出,模拟结果与实验结果有良好的一致性。图4b给出了机织复合材料在冲压后的剪切角的分布。从图4可以看出,最大剪切角发生在球形区和平面区的过渡处、沿冲头中心到角点的对角线上。该分布图与剪切框架试验中得到的剪切锁定角(shear locking ang le)相结合可以用来预测机织复合材料中出现的褶皱现象。

图4 变形后机织复合材料的剪切角分布

为了进一步分析非正交本构模型下的冲压结果,在变形后机织复合材料的边界轮廓上提取了图4a所示A至L点的缩进量s,并与相应的实验结果[5]进行比较。A、L和E(EX和EY)三个点为机织复合材料中的三个顶点,除此之外的点均是沿着变形前机织复合材料的长度和宽度进行平分而得到的。

对比图5所示的实验结果和模拟结果可知,总体来说,模拟结果和实验结果[6]具有良好的一致性。

图6所示为模拟与实验中机织复合材料变形后的边界轮廓对比。可看出,除了在X方向上有一点出入外,模拟分析得出的边界轮廓与实验结果吻合得很好。

进一步对比了图4a所示斜线上的剪切角 ω分布(实验与模拟结果),如图7所示,考虑到实验数据的离散性,两种结果基本一致。其中实验结果中最大剪切角为39.5°,而模拟分析中的相应数值为34.9°,且最大剪切角的区域均发生在点5附近。

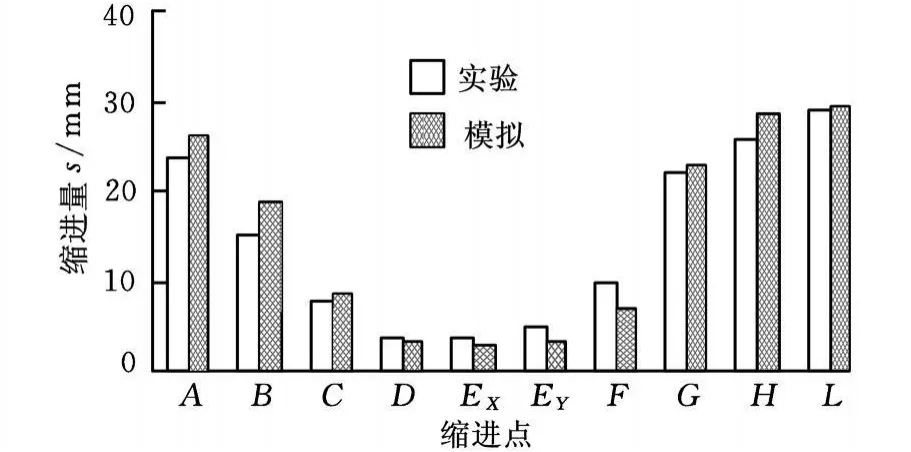
图5 实验与模拟的机织复合材料缩进量对比图

3 结论

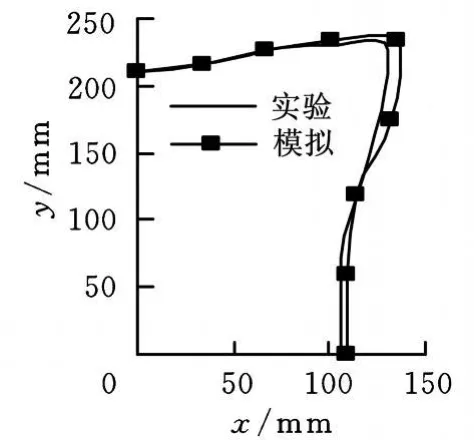
图6 边界轮廓实验与模拟结果对比图

(1)本文通过建立双球形冲压装置对平纹机织复合材料进行模拟分析,利用作者之前建立的非正交本构模型描述了机织复合材料在大变形下所引起的非线性各向异性材料行为。提取了变形后机织复合材料的边界轮廓、缩进量以及剪切角并与实验结果进行对比,对比结果的一致性验证了非正交本构模型在机织复合材料冲压成形中的有效性和正确性。

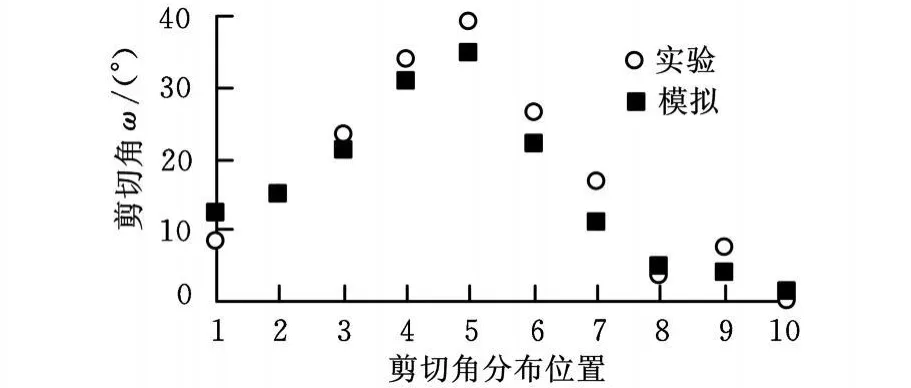
图7 剪切角实验与模拟结果对比图

(2)用非正交本构模型进行冲压模拟的最大优点就在于其简单性,容易实行,并且计算量不大,它为机织复合材料的冲压工艺流程设计提供了理论基础。应用非正交本构模型的用户材料子程序准确地预测了机织复合材料在变形中的材料行为。

[1] van West B P,Pipes R B,Keefe M.A Simu lation of the Draping of Bi-directional Fabrics over A rbitrary Surfaces[J].Journal of the Tex tile Institute,1990,81(4):448-460.

[2] Laroche D,Vu-Khanh T.Form ing of W oven Fabric Com posites[J].Journal of Com posite Materials,1994,28(18):1825-1839.

[3] Yu W R,Pourboghrat F,Chung K,et al.Nonorthogonal Constitutive Equation for W oven Fabric Reinforced Thermo-plastic Composites[J].Composites Part A,2000,33(8):1095-1105.

[4] Boisse P,Gasser A,H agege B,et al.Analysis of the Mechanical Behaviour o fW oven FibrousMaterial Using Virtual Tests at the Unit Cell Level[J].International Journal of Materials Science,2005,40(22):5955-5962.

[5] Peng X Q,Cao J.A Continuum Mechanics Based Non-orthogonal Constitutive Model for Woven Composite Fabrics[J].Composites Part A,2005,36(6):859-874.

[6] Khan M A,M abrouki T,V idal-SalléE,et al.Numerical and Experimental Analyses of Woven Composite Rein forcement Forming Using a H ypoelastic Behaviour.App lication to the Double Dome Benchmark[J].Journal of Materials Processing Tec.,2010,210(2):378-388.

[7] ten Thije R H W,Akkerman R.A Mu lti-layer T riangular Membrane Finite Element for the Forming Simu lation of Lam inated Composites[J].Composites Part A,2009,40(6):739-753.

[8] Lin H,Clifford M J,Long A C,et al.Finite Element M odeling o f Fabric Shear[J].Modeling and Simulation in Materials Science and Engineering,2009,17(1):1-22.

[9] Cao J.Woven Composites Benchmark Forum[EB/OL].Evanston,I L:Northwestern University,2006[2010-01-16].http://www.w ovencom posites.org.

[10] Ogden R W.Non-linear Elastic Deformations[M].W est Sussex:Ellis Horw ood Lim ited,1984.

[11] Boisse P,Gasser A,H ivet G.Analyses of Fabric Tensile Behavior:Determination of the Biaxial Tension-strain Surfaces and Their Use in Forming Simulations[J].Composites Part A,2001,32(10):1395-1414.

[12] Peng X Q,Cao J.A Dual Homogenization and Finite Element App roach for M aterial Characterization of Textile Composites[J].Composites Part B,2002,33(1):45-56.

Forming Simulation of Textile Composite Stamping on Double Dome

Zia-U r-Rehman1Peng Xiongqi2Shi Shaoqing3Ding Fangfang1
1.Northwestern Polytechnical University,Xi'an,710072
2.Shanghai Jiao Tong University,Shanghai,200030
3.Logistical Engineering University,Chongqing,401311

Thepaper presented a fully continuum mechanics-based approach for stamping simulation o f tex tile fiber reinforced com posites by using finite element(FE)method.A non-orthogonal constitutive model was used to represent the anisotropicmechanical behavior of tex tile composites under large shear deformation during stamping.Simu lation w as performed on a balanced p lain weave com posite over a benchmark doub le dome device.A user material subroutine UMA T for the woven com posite was developed for comm ercial FE package ABAQUS/Standard to imp lem ent the algorithm.Them ain advantage of this app roach lies in its ease execution whilst computationally effective.Simulation resu lts show good agreement w ith experimental output in term s of a num ber of parameters selected for com parison.

textile composite;finite element analysis;form ing simulation;double dome;nonorthogonal constitutivem odel

TB332

1004—132X(2011)06—0728—04

2010—03—23

国家自然科学基金资助项目(50975236);西北工业大学基础研究基金资助项目(W 018103)

(编辑 苏卫国)

Zia-U r-Rehman,男,1981年生。西北工业大学机电学院硕士研究生。主要研究方向为复合材料成形。发表论文 3篇。彭雄奇,男,1970年生。上海交通大学塑性成形工程系教授、博士研究生导师。石少卿,男,1967年生。后勤工程学院军事建筑工程系教授、博士研究生导师。丁纺纺,女,1986年生。西北工业大学机电学院硕士研究生。