一种新型串联中医推拿机械臂的机构综合和工作空间分析

谢 俊 匡俐辉 马履中 杨启志

江苏大学,镇江,212013

一种新型串联中医推拿机械臂的机构综合和工作空间分析

谢 俊 匡俐辉 马履中 杨启志

江苏大学,镇江,212013

针对中医推拿的按、揉、滚、振4种推拿手法,从型综合方面对推拿机器人机械臂进行结构设计,采用Denavit-Hartenberg法,通过齐次坐标变换,建立了机械臂的运动学模型,并对其正运动学方程进行了求解。基于图解法对推拿机械臂工作空间进行分析,得知推拿机械臂大小臂长度应相等。同时,基于蒙特卡罗原理,通过M ATLAB编程对六自由度推拿机械臂的工作空间进行了数值解的描绘,结果表明,推拿机械臂的工作空间内部工作点密集且分布均匀,满足推拿动作高效作业的要求。

推拿机械臂;型综合;工作空间;图解法;蒙特卡罗原理

0 引言

推拿作为一种医疗保健手段已经发展了两千多年,它通过手法和力量变化对经络穴位进行刺激来提高免疫系统的能力,达到预防、治疗老年腰腿疼痛的目的。然而,中医推拿实际推广过程中,各大医院的临床治疗仍由有经验的推拿师人工进行,一个疗程下来推拿师所付出的体力非常巨大。虽然近年来人们研制了许多推拿按摩器械,丰富、扩大了推拿保健和治疗的范围,但因其机械力度难以掌握,振动频率不易控制,许多器械推拿还不能达到高水平推拿师手法治疗的效果。所以开发智能推拿机器人,继承和发扬中医推拿的技巧,使古老推拿术得到较大力度的推广,是十分有现实意义的。

1 推拿机械臂的型综合

当前,机械臂的结构设计常采用的方法是机械臂的机构运动综合,它主要以运动学要求为依据,其内容包括确定机器人机构的型式(型综合)和与运动有关的几何尺寸参数(尺寸综合)。

机械臂的运动综合以使末端执行器实现被操作物体的运动要求为基本准则,考虑到机械加工性、动力传输及运动控制等问题,推拿机械臂的型综合[1]是在确定机械臂结构参数之前,根据要实现的按、揉、滚、振4种推拿手法来确定机械臂机构的自由度、组成型式、关节数目和配置方式。型综合有位置和姿态两方面要求,因此,根据推拿要求,推拿机械臂的结构设计[2-3]将机械臂分成臂和手腕两部分,通常将位置结构部分称为机器人的臂部,而将姿态结构部分称为机器人的腕部(或手腕)。

1.1 选型原则

实现上述手法的纯并联机构有三平移三转动和三平移两转动并联机构。但这两种机型属于多自由度并联机型,结构复杂,正反解计算困难,控制困难,其工作空间小。由于患者的身高、体型差异性,要求推拿头提供足够的灵活运动的空间,所以本文以基于2-P-R-R三自由度并联机构作为并联头(P表示移动副,R表示转动副),提出将少自由度并联机构与串联机械臂配合使用,共同完成推拿动作。

机械臂作为推拿机器人的主要执行部件,其功能是将末端执行器移至接近推拿的位置,所以有以下选型原则:①要使并联头能够自由地处在空间任意位置,推拿机器人的腕部必须具有3个转动自由度;②由于要实现4种推拿动作和大范围的位移调整,故除需满足推拿手法外,串联机械臂还用来提供推拿的位置,需要有x、y、z三个方向的平动;③为使患者不必躺在推拿床上进行推拿,可以方便地以站立、坐、躺等各种姿势接受治疗,串联机械臂必须保证具有足够大的工作空间;④由于推拿机器人动作频率高,所以机械臂的结构稳定性要求较高。

1.2 选型结论

基于以上的选型分析,对于推拿机械臂而言,可以得出以下选型结论:①机械臂的基体选择关节型机械臂最为合适,它包括腰部、大臂、小臂三部分,其动作灵活、工作空间大、占地面积小的优点很适合推拿的动作要求;②在以关节坐标型机械臂为基体的基础上,手腕应具有3个自由度,通常是3个转动副,它决定了末端执行器的作业姿态;③使用偏置型的关节型机器人可以保证机械臂结构的整体稳定性。

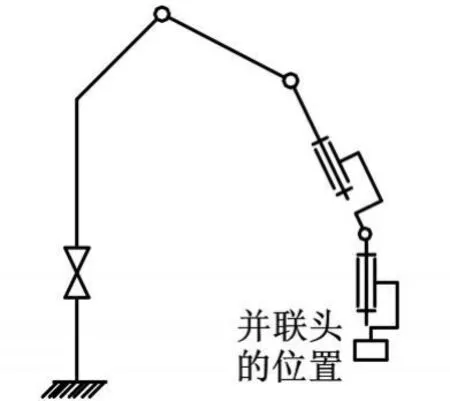
图1 推拿机械臂简图

从推拿机械臂的机构简图(图 1)可以看出,推拿机械臂具有腰部转动、大臂仰俯、小臂摆动及手腕的三自由度运动,是一种6R型串联关节型推拿机械臂。

2 机械手运动学分析

推拿机械臂有6个关节,前3个关节确定手腕参考点的位置,后3个关节确定手腕的方位。关节1的轴线为铅直方向,关节2和关节3的轴线水平且平行,距离为d3,关节1和关节2的轴线垂直相交,关节3和关节4的轴线垂直相错。运用Denavit-Hartenberg法(D-H法)得到机械手参数,如表1所示,确定连杆的坐标系位置如图2所示。表1中,αi-1为相邻运动副轴线间的夹角;ai-1为相邻运动副轴线间的公垂线的长度;di为z轴上两条相邻的公垂线间的距离;θi为运动副两条相邻的公垂线间的夹角。

表1 机械臂的D-H参数

图2 机械手臂D-H坐标系

相邻坐标系的D-H变换矩阵为

而第i坐标系相对于底座坐标系位置的齐次变换矩阵0iT是各齐次变换矩阵i-1i T的连乘积,根据式(1)可以得到以下变换矩阵:

其中 ,si=sinθi,ci=cosθi,sij=sin(θi+θj),cij=cos(θi+θj)。

式(2)描述了末端关节坐标系相对于基坐标系的位姿。

3 机械手工作空间的分析

3.1 基于图解法的推拿机械臂工作空间分析

根据推拿机械臂的结构分析,为实现机械手臂端部空间中的任意位姿,需要机构具有6个自由度,一般机构设计成2个连杆系统:前3个自由度构成的连杆称“主连杆”系统,又称“手臂”,其尺寸较大,用来实现手臂末端的空间位置;后3个自由度的杆臂尺寸较小,用来实现手臂末端的姿态,称为“次连杆”系统,又称“手腕”。机器人的工作空间是由“主连杆”的几何参数[6]决定的。机械臂主连杆的参数如图 3 所示 ,当 l2、l3、θ2min、θ2max、θ3min、θ3max已知时,即可确定最大的工作空间截面。其中,正负号表示其转动的方向,规定逆时针为负,实际代入公式中无需考虑正负号。

图3 主连杆机构

如图3所示,关节O、E运动产生了四段圆弧构成的平面封闭域ABCDA,即由以O为圆心的AB弧与CD弧、以E为圆心的AD弧以及以F为圆心的BC弧组成,此即为工作空间截面形状。对应的特征点有 A 、B 、C、D 、E 、F,其坐标分别为

设R和r分别为圆弧AB和圆弧CD的半径,则

3.2 基于数值法的推拿机械臂工作空间分析

目前,随着计算机的广泛应用,对机械臂工作空间的分析越来越倾向于数值解法,用数值法计算机械臂的工作空间不仅直观性强,而且不容易受到自由度数目的限制,方法简便、节省时间。基于蒙特卡罗法[7-8]并利用MATLAB强大的编程和图形显示能力对推拿机械臂的工作空间进行数值解的描绘,结合正运动方程,容易形成通用的程序,适合于任何关节型机械手工作空间的求解,且对关节变量的变化范围没有限制。

根据图4所示的程序框图,取d3=160mm,d4=500mm,a2=500mm,a3=-15mm,转角的变化范围见表1,编制MA TLAB程序,其运行结果如图5所示,得到了机械手的三维可达工作空间的形状和大小,并通过输入 View(0,0)、View(90,0)、View(0,90)命令,分别得到工作空间的xz平面、yz平面和xy平面的形状和大小(图5～图8)。

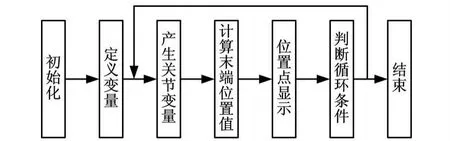
图4 机械手作业空间程序框图

图5 机械手工作空间三维图

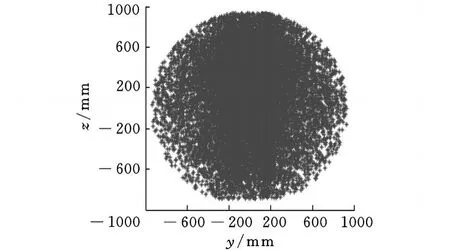
图6 工作空间xz投影面

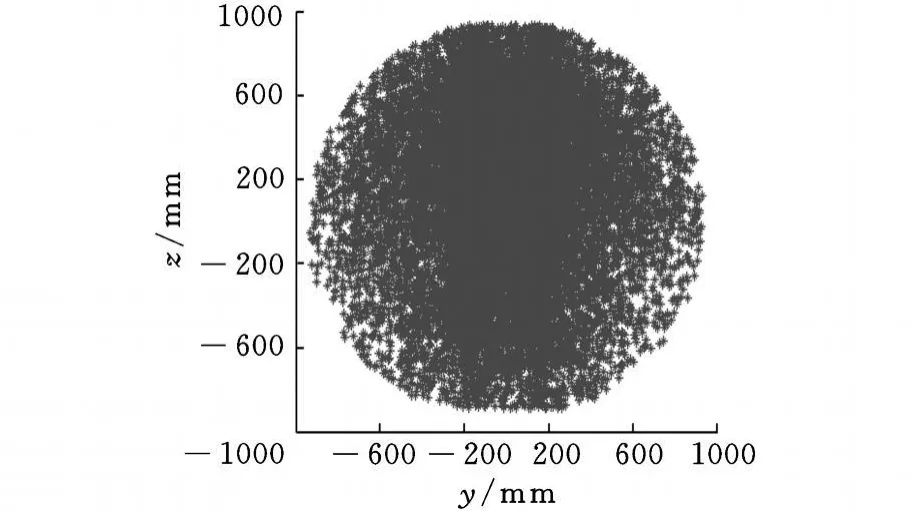
图7 工作空间yz投影面

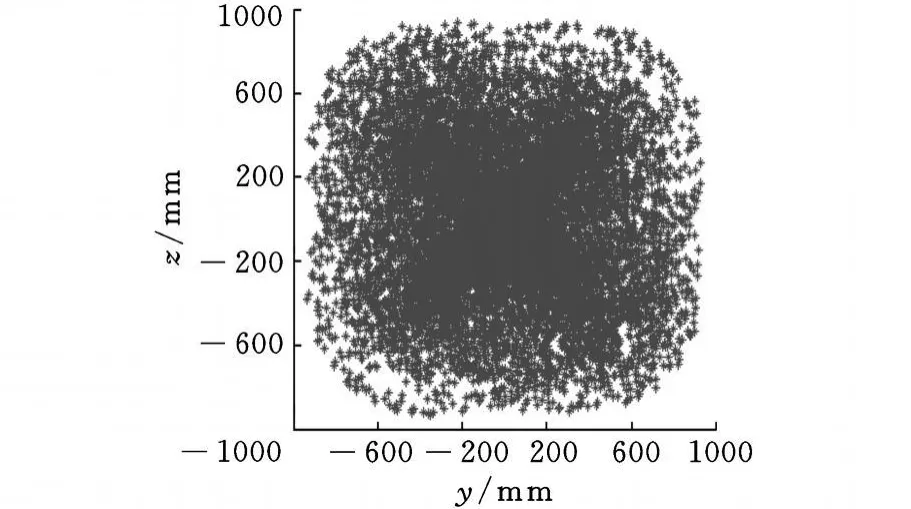
图8 工作空间xy投影面

3.3 工作空间的分析结论

推拿机器人属于机械手臂系列机器人,机械臂的设计首先必须满足工作空间的要求。工作空间是从几何方面衡量机械手工作能力的主要运动学指标之一,也是设计机械臂的重要依据,其实质是机械手占有空间的体积。上述两种方法均是给定机械臂的具体结构形式和结构参数以及关节变量的变化范围,求工作空间,属于工作空间正问题。

通过图解法来求解机械臂的工作空间边界,得到工作空间的各类剖截面或是剖截线,具有直观性强的特点。

用数值法计算机械臂的工作空间不仅直观性强,而且不容易受到自由度数目的限制,方法简便,节省时间。同时在规划机械臂的轨迹时,为了避免机械臂运动过程中奇异[9]现象的出现,所选取的轨迹点应尽量远离边界点。

4 结论

(1)从臂部与腕部两方面分别进行机械臂选型设计,选用6R型串联关节型推拿机械手。采用D-H坐标系,通过齐次变换法求解得到正运动学方程,该方程是进行机械臂运动控制及动力学分析的基础,也是进行空间分析和轨迹规划的前提。

(2)基于图解法的推拿机械臂工作空间分析可知,当l2+l3之和一定时,l2=l3时工作截面面积最大,所以选型时选用大小臂长度相等,从而完成了对机械臂的尺寸优化。

(3)基于蒙特卡罗法并利用MA TLAB编程得到了机械臂工作空间数值解的描绘,此方法不受关节变量类型和关节变化范围限制,是求解机械臂工作空间可靠的数值计算方法,具有计算速度快、求解简单等特点。对于推拿这样点到点的工作形式,蒙特卡罗方法得到的散点图形显示更为直观形象,增强了机械手工作空间的数值仿真效果。

[1] 马香锋.机器人机构学[M].北京:机械工业出版社,1991.

[2] 蔡自兴.机器人学[M].北京:清华大学出版社,2000.

[3] 熊有伦.机器人技术基础[M].武汉:华中理工大学出版社,1996.

[4] 杨廷力.机器人机构拓扑结构学[M].北京:机械工业出版社,2003.

[5] 余顺年,马履中,郭宗和.中医推拿手法运动学及动力学特征分析[J].山东理工大学学报,2005,19(3):82-85.

[6] 梁喜凤,王永维,苗香雯,等.番茄收获机械手工作空间分析与仿真[J].浙江大学学报(农业与生命科学版),2005,31(6):807-811.

[7] 范波涛,张良.蒙特卡洛方法在喷浆机器人工作空间分析中的应用[J].山东工业大学学报,1999,29(2):146-151.

[8] Rastegar J,Fardanesh B.M anipulator Workspace Analysis Using the Monte Carlo Method[J].Mech.M ach.Theory,1990,25(2):233-239.

[9] Gursel A.Determ ination of Singu larity Contours for Five-bar Planar Parallel Manipu lators[J].Robotica,2000,18(5):569-575.

Type Synthesisand AnalysisofWorkspace of a Novel Series ChineseM edicalM assage Arm

Xie Jun Kuang Lihui M a Lǜzhong Yang Qizhi
Jiangsu University,Zhenjiang,Jiangsu,212013

Based on theChinesemedicalmassagemanipulation of pressing,kneading,rolling,and vibrating method,from aspects of type-synthesis and dimension-synthesis,the design ru les o fmechanical arm of Chinesemedicalmassagemanipu lator were introduced.A t the same time,themassage mechanical arm's kinematicsmodelw as established by meansof the homogeneous coordinate transformation using the Denavit-Hartenberg coordinate system.Its forward kinematics was solved.The workspace of this Chinesemedicalmassage arm wasanalyzed by graphicalapproach.It show s that the length of upper arm and forearm of this kind of Chinese medical massage arm must be equal.The workspace of this Chinesemedicalm assage arm was also portrayed based on the Monte Carlo p rinciple through programming on MATLAB.It indicates that the working points in the workspace of this massagemechanicalarm are distributed compactly and uniform ly,which can satisfy theChinesem edicalm assage requirementsw ith high efficiency.

massagemechanical arm;type-synthesis;workspace;graphical approach;Monte Carlo p rinciple

TH 115

1004—132X(2011)06—0697—05

2010—03—17

国家高技术研究发展计划(863计划)资助项目(2008A A040205);国家自然科学基金资助项目(50905077);高等学校博士学科点专项科研基金资助项目(SRFDP:2009327120007);江苏省博士后基金资助项目(0901010B)

(编辑 苏卫国)

谢 俊,女,1968年生。江苏大学机械工程学院副教授。主要研究方向为并联机构及其应用、智能材料及其应用、振动控制、流体机械特性及流动模拟等。发表论文 30余篇。匡俐辉,男,1986年生。江苏大学机械工程学院硕士研究生。马履中,男,1939年生。江苏大学机械工程学院教授、博士研究生导师。杨启志,男,1974年生。江苏大学机械工程学院副教授。