基于神经网络的超磁致伸缩传感执行器磁滞模型

刘慧芳 贾振元 王福吉

大连理工大学精密与特种加工教育部重点实验室,大连,116024

基于神经网络的超磁致伸缩传感执行器磁滞模型

刘慧芳 贾振元 王福吉

大连理工大学精密与特种加工教育部重点实验室,大连,116024

依据超磁致伸缩材料Joule效应和Villari效应之间的耦合关系,提出一种超磁致伸缩传感执行器,该执行器利用Villari效应和Faraday效应产生的感应电动势驱动超磁致伸缩材料发生Jou le效应而产生应变,给出了该传感执行器的结构和工作原理。为了解决材料的磁滞对超磁致伸缩传感执行器输出特性的影响,测量了在不同预紧力和最大工作电流作用下的磁滞回线,采用BP神经网络建立了磁化滞回模型。计算结果表明该模型能很好地描述在任意预紧力和最大工作电流等工作条件下的磁滞特性。

超磁致伸缩;传感执行器;磁滞;神经网络

0 引言

超磁致伸缩材料具有两种重要的物理效应:一是在外磁场作用下长度发生变化的 Joule效应;二是对材料施加压力或张力,磁化强度随之改变的Villari效应[1]。应用Jou le效应可制成精密执行器[2-3],而利用Villari效应可制成力/应变传感器。本文提出一种超磁致伸缩传感执行器,它根据两效应之间的耦合关系,利用Faraday效应产生的感应电动势,在外部功率放大电路帮助下驱动超磁致伸缩材料发生应变,它同时具有传感和执行功能。

超磁致伸缩材料的一个显著缺点是存在磁滞,磁滞的存在严重影响了系统的输出特性,所以,为了实现精确控制,必须建立能够描述多种工作条件下磁滞特性的磁滞模型。目前,描述磁滞特性的主要方法有实验法、Preisach模型和J-A模型。实验法需要测定大量数据,实施较为困难,且无法得到任意工作条件下的磁滞回线;Preisach模型可以描绘不同变化历程中的磁滞回线,但在考虑频率及各向异性等多种因素情况下模型变得复杂,难以求解[4-5];J-A模型参数多,并且很难准确辨识。

神经网络是建立输入输出之间非线性关系的一种有效黑盒子工具[6-7],一些学者已经开始利用神经网络研究磁滞模型[8-11],但尚未对在预紧力及电流等多种工作条件下的磁滞特性进行研究。本文采用BP神经网络,构造了在不同预紧力和最大电流作用下的超磁致伸缩传感执行器磁滞模型,实现了对磁通密度方便准确的计算。

1 超磁致伸缩传感执行器工作原理

超磁致伸缩传感执行器的工作原理是:在外部力作用下,利用V illari效应和Faraday效应在线圈中产生的感应电动势,在解耦电路和控制系统的帮助下驱动超磁致伸缩材料发生Jou le效应而产生应变,工作原理如图1所示。外部力的作用使超磁致伸缩棒发生Villari效应,内部磁通密度产生变化,进而发生Faraday电磁效应导致线圈内产生感应电压u m,与初始激励电压u叠加耦合构成超磁致伸缩传感执行器的控制电压uc。通过外部解耦电路从u c中提取出传感信号u m,一方面经过信号放大、滤波处理后采集到计算机内,与传感过程的数学模型结合,可计算出传感执行器所承受的外部作用力以及产生的位移;另一方面,计算机控制系统将处理后的感应电压经过数据保持和D/A转换,以及功率放大器放大后作为驱动电压驱动传感执行器。因此,超磁致伸缩传感执行器不仅具有感知外部作用力和位移的传感功能,同时实现了以外部力产生的感应电压驱动自身执行的过程。

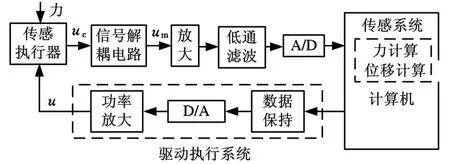
图1 超磁致伸缩传感执行器工作原理图

2 超磁致伸缩传感执行器结构

超磁致伸缩传感执行器结构如图2所示,核心元件——超磁致伸缩棒安装在线圈骨架腔体内,上下表面分别与上导向块和下导磁垫片接触,通有电流的激励线圈为超磁致伸缩棒提供工作磁场。电工纯铁材料的上导磁体、上导向块、下导磁垫片、下导向块、下导磁体、圆筒磁轭与超磁致伸缩棒构成封闭磁回路,对磁通进行引导,降低了漏磁,使超磁致伸缩棒在一定的激励电流作用下其内部具有较高的磁通密度,并且保证其内部磁通密度均匀分布。霍尔传感器通过非导磁性胶粘贴在下导磁体上表面、不锈钢环内部,用来测量实际磁通密度。为了提高霍尔传感器测量磁通密度的灵敏度,根据磁路特性提出在其周围采用不锈钢环结构,其原理是磁通总是穿过磁阻较小的路径,不锈钢环的磁阻同霍尔传感器及周围空气相似,因此磁通能够平均穿过霍尔传感器及其周围结构。通过调节安装在顶盖上的4个螺钉,配合碟形弹簧为超磁致伸缩棒提供可调的预紧力。外套、顶盖和底盖是非导磁性不锈钢材料,将整个传感执行器结构封装在内部,防止外界环境对内部磁路的干扰。

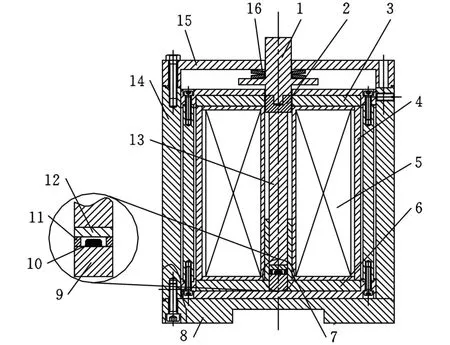
图2 超磁致伸缩传感执行器结构图

3 磁场特性有限元分析

在超磁致伸缩传感执行器内部,采用霍尔传感器测量与超磁致伸缩棒磁通密度成比例的磁通密度,并采用有限元方法分析其内部磁场特性。在ANSYS软件环境中,建立传感执行器的二维轴对称几何模型,采用空气远场单元模拟磁场中的远场耗散,从麦克斯韦方程组出发,分析计算磁场强度及磁通密度等特性。结果表明:磁通主要分布在由超磁致伸缩棒、上导磁体、上导向块、下导磁垫片、下导向块、下导磁体和圆筒磁轭构成的闭合磁回路内,漏磁很小;超磁致伸缩棒和霍尔传感器内部磁通密度较均匀,因此在建模过程中可用平均值代替两者内部的实际磁通密度。平均磁通密度分别为1.033T和0.455T,两者之间的比例系数约为2.27。因此,超磁致伸缩棒内部磁通密度可根据霍尔传感器测得的磁通密度计算得到:

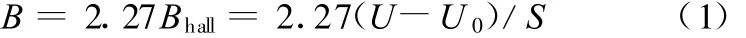
式中,B为超磁致伸缩棒内部磁通密度;B hall为霍尔传感器内部磁通密度;U为霍尔传感器输出电压;U0为霍尔传感器静态电压;S为霍尔传感器灵敏度。

4 磁滞回线测量实验

我们根据图2的设计研制超磁致伸缩传感执行器,并建立测量其磁滞特性的实验系统,如图3所示。其中超磁致伸缩棒的尺寸为 φ12×100mm,材料为TbDyFe。双极性可编程电源为激励线圈提供可控直流电流,通过应变片测量碟形弹簧的应变来实现对预紧力的测量,采用万用表测量霍尔传感器的输出电压。本文测量了预紧力分别为 0、103N、160N、235N、315N、403N、488N 、580N 、675N 、762N,最大工作电流分 别为1A、1.5A、2A、2.5A时的磁滞回线,共测得 1100组数据。经过式(1)计算,得到超磁致伸缩棒的磁通密度,图4所示为580N预紧力作用下测得的4组磁滞回线。

图3 磁滞回线测量实验系统

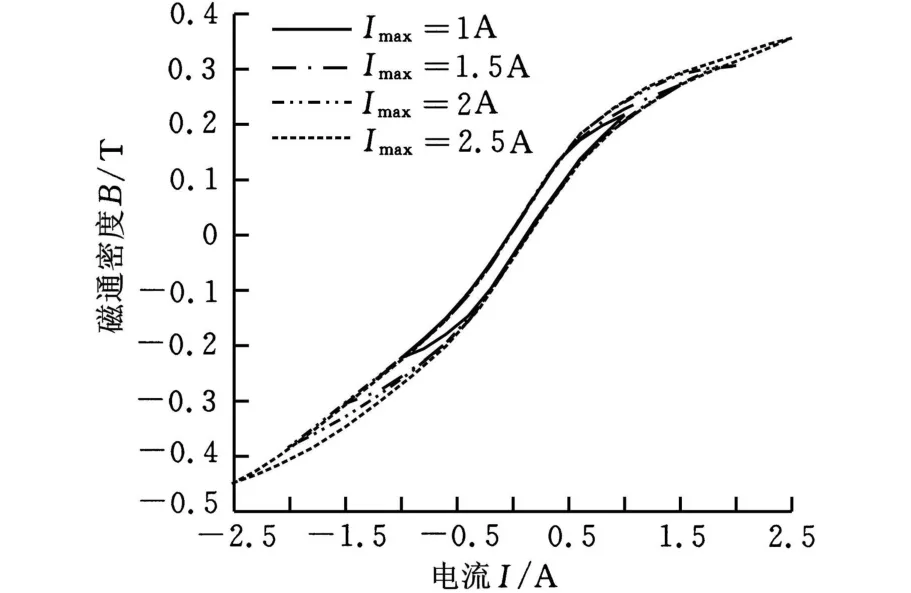
4 580N预紧力作用下磁滞回线(I max为最大工作电流)

实验结果表明磁通密度与激励电流之间关系具有明显的非线性,工作电流仅在-0.5A～0.5A范围内,两者之间具有较好的线性关系。

5 超磁致伸缩传感执行器磁滞特性神经网络建模

5.1 BP神经网络原理

BP神经网络是一种单向传播的多层前馈网络,由输入层、中间层(隐含层)和输出层组成。上下层之间全部全连接,而每层神经元之间无连接。当一组学习样本提供给网络后,神经网络的激活值从输入层经各中间层向输出层传播,在输出层的各神经元获得网络的输出结果。接下来,以网络输出与目标输出的均方差最小为目标,从输出层经各中间层逐层修正各连接权值,最后回到输入层,从而实现输入与输出之间的映射关系。

BP算法可以使权值收敛到某个值,但不能保证其为误差平面的全局最小值,这是因为采用梯度下降法可能会产生一个局部最小值。因此,本文采用改进后的算法,即通过附加动量法来解决此问题。采用动量法来反向修正隐含层权值和阈值的计算公式为[12]

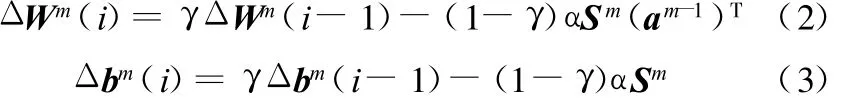
式中,ΔW为隐含层权值变化值;Δb为隐含层阈值变化值;γ为动量项因子;a为学习率;S为隐含层一般化误差;α为训练样本数据;m为第m组训练样本;i为修正次数。

5.2 应用分析及样本数据选取

在超磁致伸缩传感执行器中,决定超磁致伸缩棒磁通密度的主要因素包括激励电流、最大工作电流、预紧力、工作电流的变化趋势(电流增大称为磁滞回线升程,反之为回程),分别用I、I max、Fpre、k(k=1代表升程,k=-1代表回程)表示,B表示磁通密度。其磁化关系可描述为

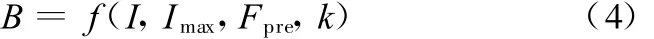
预紧力、最大工作电流等工作条件之间的相互关联性使系统的磁滞建模非常困难,然而神经网络却可以仅仅借助样本数据,无需建立系统的数学模型,就可以实现从输入到输出之间的高度非线性映射。

样本数据的质量和数量在很大程度上影响到神经网络的泛化能力,选择出的样本数据必须具有代表性,能体现原始数据集的整体特性,因此,利用第4节测得的磁滞数据,选取1000组数据用于模型的构建及验证。将数据分为两组,其中第一组(700组数据)用于模型构建,第二组(300组数据)用于模型验证,部分样本数据如表1所示。

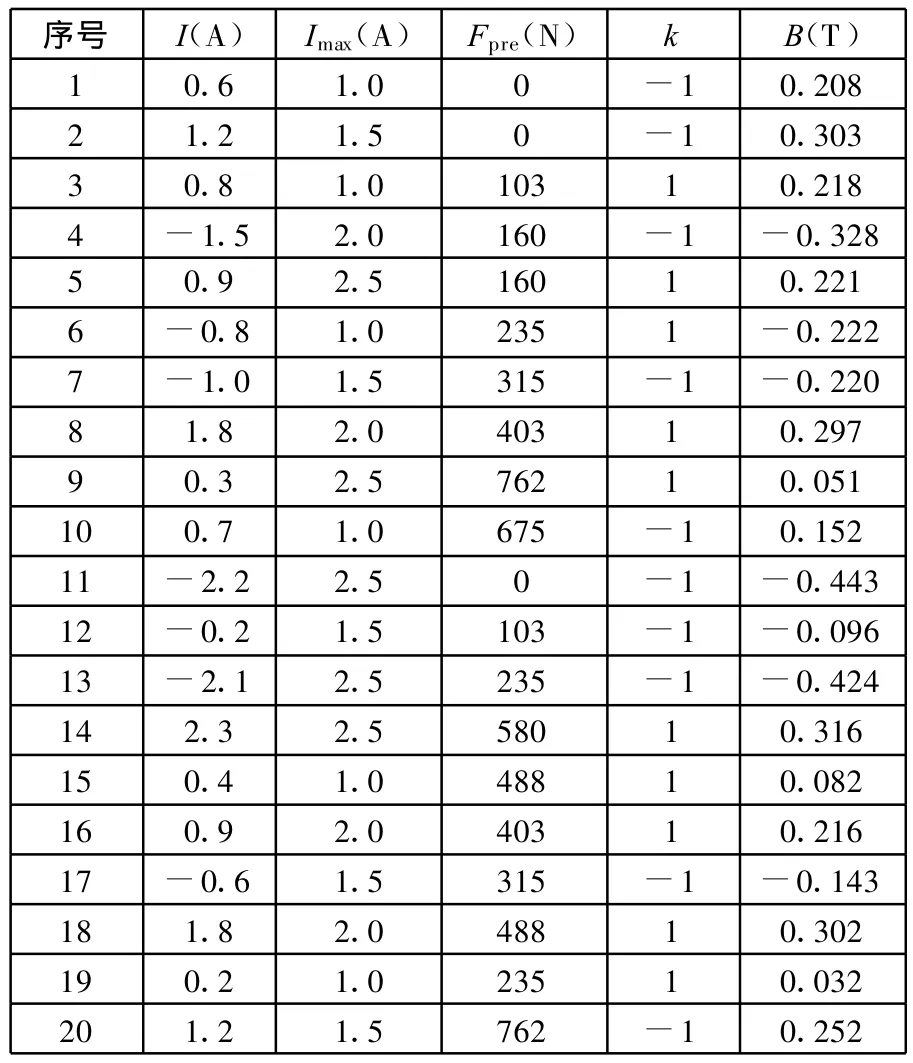
表1 部分原始数据

5.3 磁滞模型构建

本文涉及的磁滞是指在超磁致伸缩传感执行器的执行过程中磁通密度和电流之间存在的滞回。在实际工作过程中,信号解耦电路将传感和执行分解成两个独立的过程,传感对执行过程中磁通密度的计算没有影响,因此,本文对传感执行器的执行过程进行磁滞建模。影响传感执行器磁滞特性的主要因素有 4 个(I、I max、F pre、k),输出特性有1个(B),因此所建立的BP神经网络输入神经元为4个,输出神经元为1个,选取3层BP神经网络,隐含层神经元个数通过试算法确定为10个,传递函数分别取为tansig和purelin函数,学习速率和目标参数值分别设定为0.01和1×10-5,网络结构如图5所示。

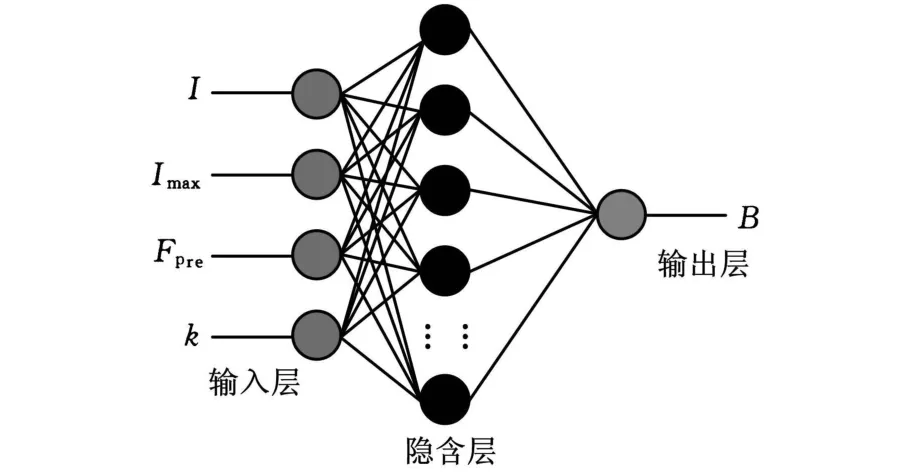
图5 神经网络结构图

选取样本数据中的第一组数据,采用Lavenberg-Marquard训练算法,在MA TLAB软件环境中对BP神经网络进行训练[13]。BP神经网络模型训练过程中的误差平方(sum of squared error,SSE)变化情况如图6所示,结果显示,经过97次迭代后收敛于所要求的误差指标。

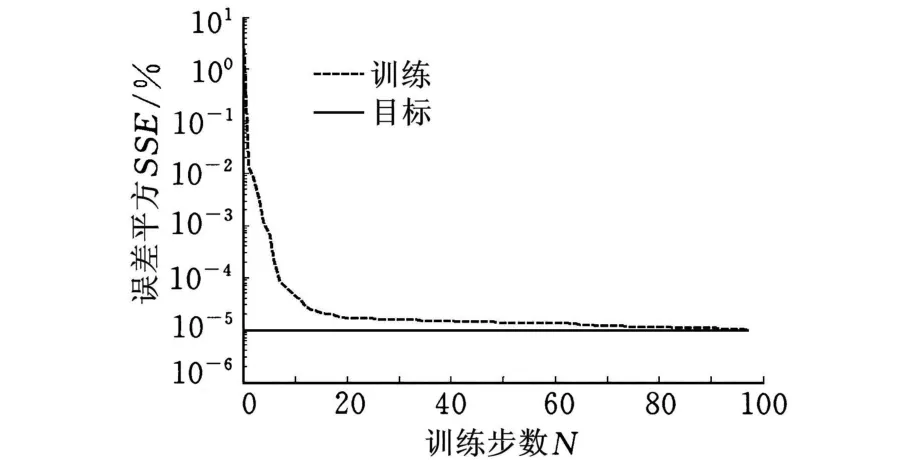
图6 神经网络模型训练过程

5.4 计算结果分析

选取第二组数据样本,对上述所构建的BP神经网络模型进行验证,磁通密度的预测结果、实际测量结果及相对误差的部分数据如表2所示。在488N预紧力和2A最大工作电流、580N预紧力和1A最大工作电流作用下的磁滞回线预测结果如图7所示。

分析预测结果可以发现,所建立的BP神经网络磁滞模型达到了较高的精度,平均相对误差为1.8%,最大相对误差为5.8%,因此可以用作描述超磁致伸缩传感执行器的磁滞特性。

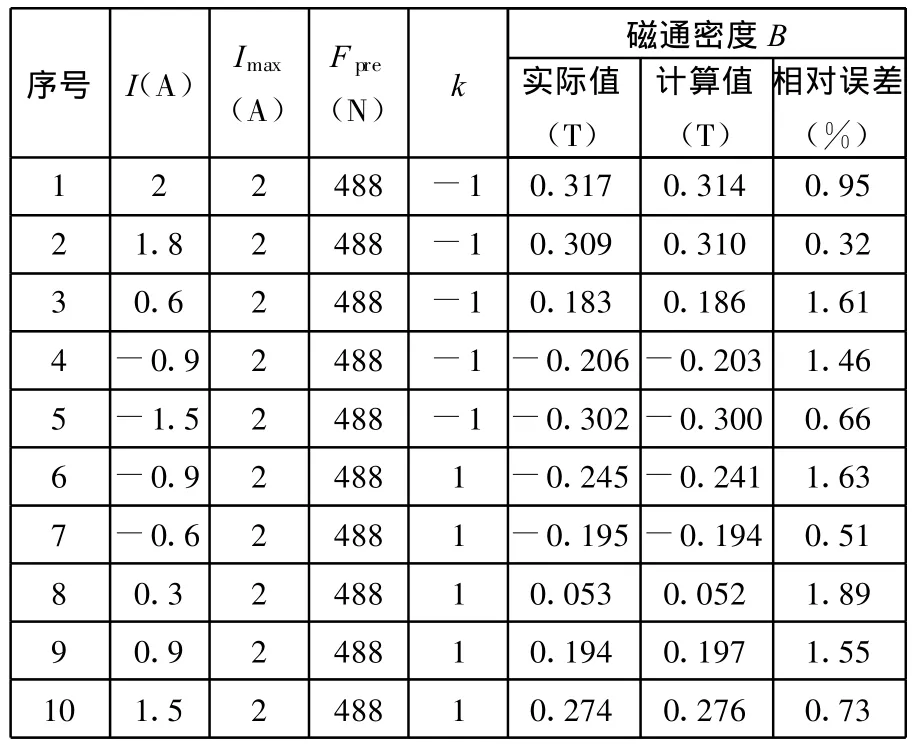
表2 预测结果(部分数据)

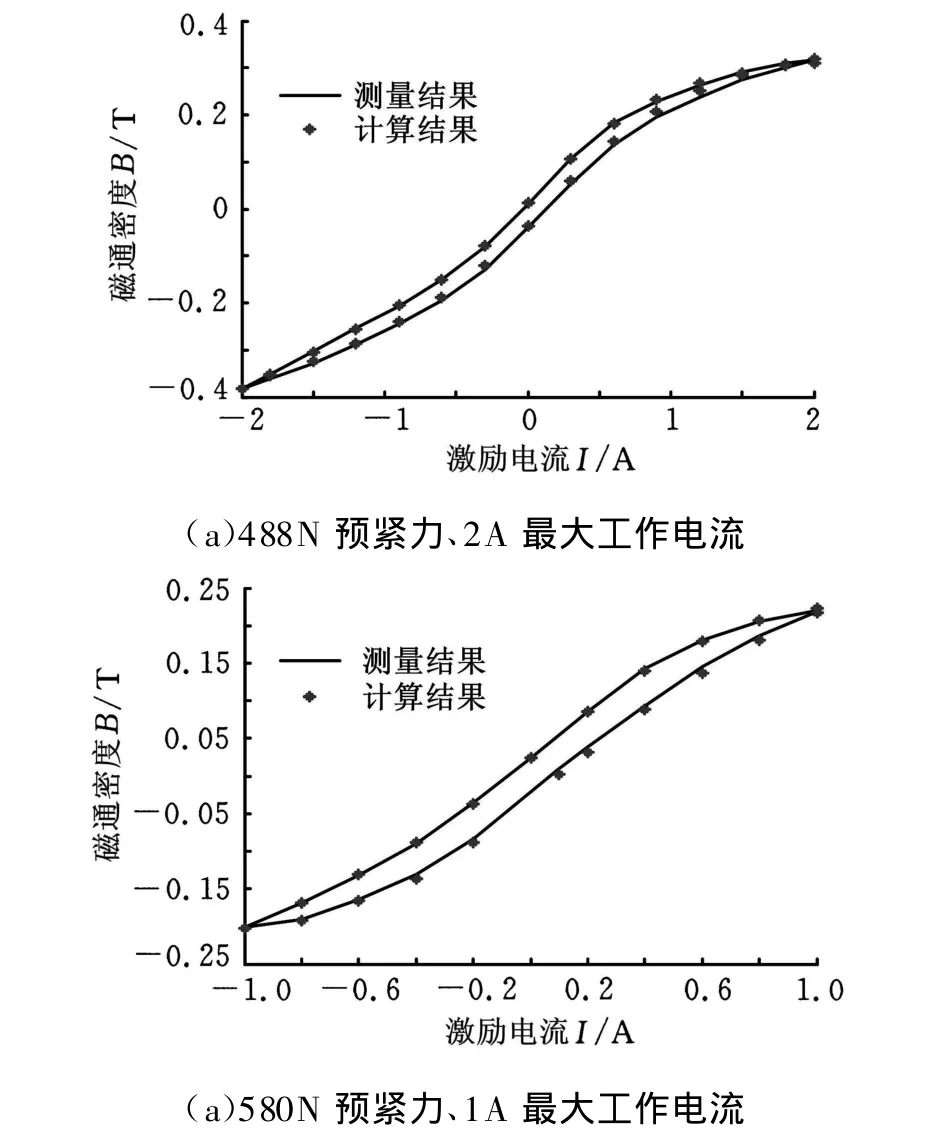
图7 磁滞回线的预测结果与实验结果对比

6 结论

(1)本文依据Jou le效应和Villari效应的耦合关系提出了超磁致伸缩传感执行器的设计方法,该方法利用Villari效应和Faraday效应产生的感应电动势,驱动超磁致伸缩材料发生Joule效应而产生应变,使其兼具传感和执行功能。

(2)采用集成在内部的霍尔传感器,结合有限元方法,通过实验得到了传感执行器在不同工作条件下的磁滞特性实际曲线。

(3)针对本文设计的传感执行器,采用BP神经网络方法,建立了在不同预紧力和最大工作电流作用下的磁滞模型,并进行仿真实验。实例表明,所建立的神经网络模型对系统磁滞特性的预测达到了较好的效果。

[1] 李扩社,徐静,杨红川,等.稀土超磁致伸缩材料发展概况[J].稀土,2004,25(4):51.

[2] 郭东明,杨兴,贾振元,等.超磁致伸缩执行器在机电工程中的应用现状[J].中国机械工程,2001,12(6):724-728.

[3] 卢全国,陈定方,钟毓宁,等.超磁致伸缩致动器热变形影响及温控研究[J].中国机械工程,2007,18(1):16-19.

[4] Zhao Xinlong,Tan Yonghong.M odeling Hysteresis and Its Inverse Model Using Neural Networks Based on Expanded Input Space Method[J].IEEE Transactions on Control Systems Techno logy,2008,16(3):484-490.

[5] 黄平林,胡虔生.基于人工神经网络的Preisach磁滞模型与实现[J].电工电能新技术,2009,28(1):43-50.

[6] Dim itre M,Luc D,M arc D W,et al.Modeling o f Quasistatic Magnetic Hysteresis w ith Feed-Forward Neural Netw orks[J].Journalof App lied Physics,2001,89(11):6737-6739.

[7] 郑军红,叶修梓,陈志扬.基于神经网络和遗传算法的智能夹具规划[J].中国机械工程,2008,19(19):2376-2381.

[8] Sixdenier F,Scorretti R,Marion R,et al.Quasistatic H ysteresis Modeling with Feed-Forw ard Neural Networks:In fluence of the Last But One Ex treme Values[J].Journalof M agnetism and Magnetic Materials,2008,320(20):992-996.

[9] Kucuk I.Prediction o f H ysteresis Loop in M agnetic Cores Using Neural Network and Genetic A lgorithm[J].Journal of M agnetism and M agnetic Materials,2006,305(2):423-427.

[10] Cincotti S,MarchesiM,Serri A.A Neural Netw ork M odel of Parametric Non-linear Hysteretic Inductors[J].IEEE T ransactions on Magnetics,1998,34(5):3040-3043.

[11] Serpico C,V isone C.M agnetic Hysteresis Modeling via Feed-Forward Neural Netw orks[J].IEEE Transactions on Magnetics,1998,34(3):623-628.

[12] 贾振元,马建伟,刘巍,等.多几何要素影响下液压阀件特性的混合神经网络预测模型[J].机械工程学报,2010,46(2):126-131.

[13] W ilamow ski B M,Kaynak O,Ip likci S,et al.An A lgorithm for Fast Convergence in Training Neural Networks[C]//Proceedings of International Joint Conference on Neural Netw orks.Washington,2001:1778-1782.博士研究生。主要研究方向为传感器、微执行器、超磁致伸缩材料及应用。贾振元,男,1963年生。大连理工大学机械工程学院教授、博士研究生导师。王福吉,男,1974年生。大连理工大学机械工程学院副教授、博士。

Study on HysteresisM odel of Giant Magnetostrictive Sensing Actuator Based on Neural Network

Liu Huifang Jia Zhenyuan Wang Fuji
Key Laboratory for Precision and Non-traditional Machining Technology of M inistry of Education,Dalian University of Technology,Dalian,Liaoning,116024

Based on the coup ling relationship between Jou le effect and V illari effect of the giant magnetostrictivem aterials,it p roposed a giantm agnetostrictive sensing actuator which used induced electromotive force generated by Villarieffectand Faraday effect to drive giantmagnetostrictivem aterialsoccurring Joule effect and generating strain.Its structure and working princip lewere presented herein.Meanwhile,in order to solve the hysteresis characteristics of the material in giantmagnetostrictive sensing actuator,hysteresis loop under different pre-tightening force and maximum working current were measured.M oreover,it put forward estab lishing them agnetization hysteresism odel of the giantmagnetostrictive sensing actuator by BP neural networks.The calculation results show that them odel can describe hysteresis characteristics under arbitrary pre-tightening force and maximum working currentw ell.It providesevidence for hysteresis compensation of giantmagnetostrictive sensing actuator.

giantmagnetostrictive;sensing actuator;hysteresis;neural netw ork

TP183;TB381

1004—132X(2011)05—0571—05

2010—05—17

国家自然科学基金资助项目(50775021)

book=51,ebook=281

(编辑 袁兴玲)

刘慧芳,女,1983年生。大连理工大学机械工程学院