铣削精加工非线性时频域颤振分析

方喜峰 仝永海 吴春桥 张胜文 汪通悦

1.江苏科技大学,镇江,212003 2.淮阴工学院,淮安,223001

铣削精加工非线性时频域颤振分析

方喜峰1仝永海1吴春桥1张胜文1汪通悦2

1.江苏科技大学,镇江,212003 2.淮阴工学院,淮安,223001

为了抑制铣削精加工过程中的颤振,针对切削动力学模型的非线性因素,引入任意封闭形式的数学分析方法,建立了时频域非线性非光滑变系数微分方程,得到了该方程的数值解。研究了切削用量和螺旋角对颤振的影响,得出了径向切深与轴向切深的非线性关系和轴向切深与进给量的关系,并通过实验验证了结论。

颤振;铣削精加工;非线性;切削用量;

0 引言

目前,国内外学者对加工过程中的颤振进行了较深入地研究。文献[1-3]采用多自由度在频域中研究颤振,对颤振进行预测,取得较好效果,但是模型忽略了很多非线性因素。师汉民[4]采用单自由度模型研究了切削过程颤振的非线性因素,引进了国外研究者提出的非线性模型,通过考虑刀具振离工件这一非线性因素,提出了更加完善的模型,较好地解释和预测了颤振振幅稳定性及外界干扰诱发的机床颤振;探讨了机床颤振的早期诊断和预测,以及数控机床的在线避振技术,即用主轴转速或进给量的扰动来抑制颤振,并提出通过振动刀架结构来实现的想法。吴雅等利用实验方法研究动态切削噪声的动态切削条件,提出振动频率主要由机床切削系统的模态固有频率所决定[5]。文献[6]指出切削颤振不仅取决于切削力的动态特性,也取决于机床结构的动态特性。另有其他学者研究了影响颤振的因素[7]。

非线性模型应用于单元切削的研究中时取得了很大成功,但是应用于铣削中时由于该单元模型忽略了铣削的断续性和其他因素,故其对铣削过程的颤振解释与实验有出入。铣削过程的断续性和多齿参与切削是单元切削所没有的,据相关文献的非线性模型和多齿切削的特点,本文计入如下的非线性因素:①切削力的周期波动性;②非线性刚度;③切削厚度的动态变化;④两个方向振动的耦合;⑤刀齿振离工件。建立了非线性模型,采用CutPro测试系统测试铣刀的模态参数,采用A ltintas开发的求斜角切削参数系统[1]求斜角切削参数,得出了一些结果。

1 模型的建立

切削模型见图1、图2,图2所示为把铣刀螺旋面展开到平面上的动态切削过程,切削过程包括以下因素:主轴转速n、每齿进给量f z、齿数N、螺旋角β、切向力系数k tc、径向力系数k rc。切削力引起的铣刀在x向和y向的总位移以Δxj和Δyj表示,合位移以 Δh(φj)表示,存在如下的关系:

从顺时针方向度量的瞬时齿位角为

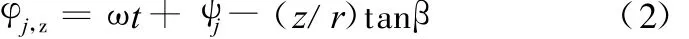
式中,φj为瞬时齿位角;z为距铣刀端部的高度;ω为角速度;ψj为第j个刀齿相对于铣刀的角位置;r为铣刀半径。

每齿进给量和相邻刀齿引起的相位延迟为

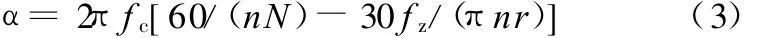
式中,fc为颤振频率。

图1 切削模型

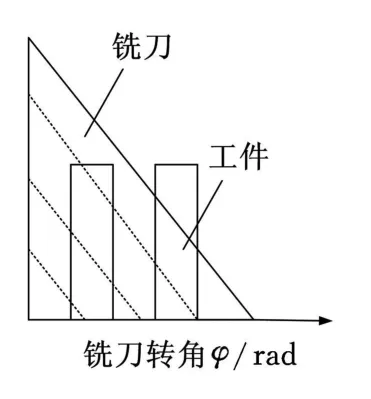
图2 铣刀动态切削过程

铣削厚度h(φj)由静态部分和动态部分组成,静态部分近似为 f z sinφj,动态部分近似为rjrj,0,即

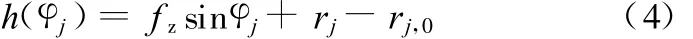
式中,rj为第j个刀齿的径向位移;rj,0为前一个刀齿的径向位移。

由于切削厚度的静态分量对颤振再生没有影响,因此在研究颤振时可以去掉它的作用,以下以Δh(φj)代替h(φj)。

斜角切削的切削力模型见文献[1]。从图2不难看出切削工件的刀齿长度是周期变化的,其导致的总切削力波动是诱发颤振的原因之一,但是比螺旋角为0°的铣刀的冲击小得多。铣削的连续性随着齿数的增多和螺旋角的增大而提高。根据文献[8],存在如下关系:

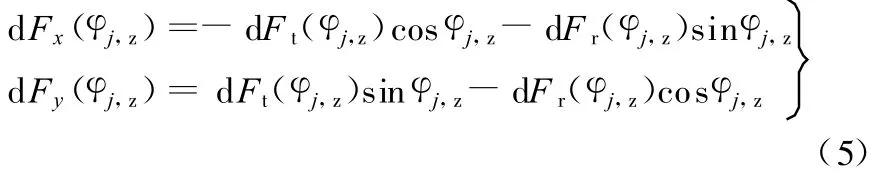
式中,Ft为切削力切向分量;Fr为切削力径向分量。

已知轴向切深a p、径向切深 a e,以及r、f、N,因干扰引起的振动为h(φj),为便于考察颤振动态过程,以h(t)表示h(φj),相继两齿的附加切削厚度 Δh(φj)以 Δh(t)表示[4],则有

式中,i为该铣刀前i个齿数;δ为切削每齿进给量指数,对不同工件材料和刀具材料取不同值;T为延迟时间,T=60/(n N)-30 f z/(πnr);c为切入率系数。

据文献[4],切削加工过程中机床的非线性刚度是一个基本特点,据此在动力学方程中计入非线性刚度项,考虑刀齿的间断和进给量的影响,由非线性刚度引起的分切削力为

式中,x(t)、y(t)分别为 x、y方向的颤振位移;mx、my,cx、cy,kx、ky分别为x、y方向的模态质量、模态阻尼和模态刚度。

解式(17),研究颤振的动态过程与切削参数、刚度和阻尼的关系。由于式(17)左端呈非线性,右端呈非光滑,而且是变系数的,故求解困难。我们需要求数值解并在频域研究颤振信号结构。

2 模型的数值解

2.1 动态切削力

根据以上方程采用MATLAB求数值解并作频域分析。工件材料为铝合金 2A 12,刀具为Fraisa硬质合金立铣刀,根据A ltintas等开发的求斜角切削参数系统获取斜角切削参数,其输入参数为摩擦角、铣刀前角、铣刀螺旋角,输出斜角切削参数和切削力系数,并采用CutPro软件测得模态参数。根据式(7)～式(12),可知总切削力可以分离为两项乘积的形式,其中一项是待求的附加动态位移Δh,另一项是与时间有关的变量,在不考虑力与位移耦合时,动态总切削力时序见图3,不考虑力与位移耦合的各齿分力时序见图4。

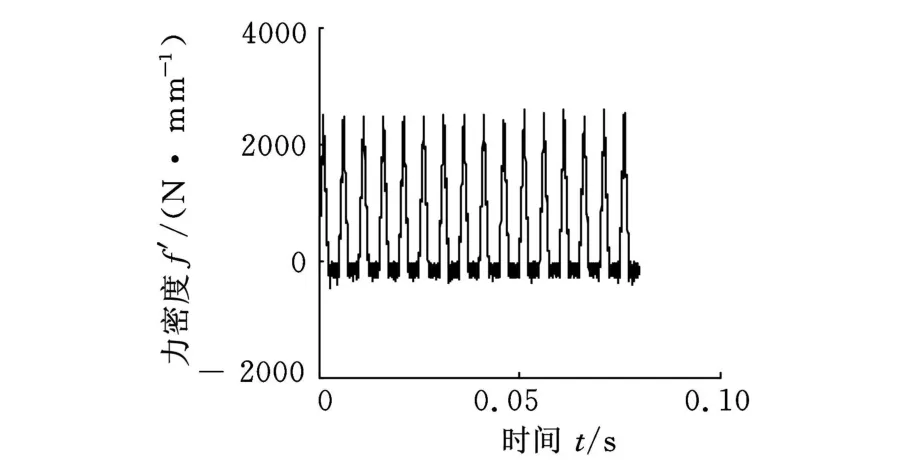
图3 总切削力时序图

图4 分切削力时序图

2.2 径向切深对颤振的影响

在初始位移为 0.01mm、刚度为3.0725×107N/mm、阻尼系数为0.031 152、固有频率为3754.2Hz的情况下,研究径向切深对颤振的影响,如图5所示,其中,图 5a、5b所示分别是转速为13 000r/min,轴向切深1mm,径向切深3mm,每齿进给量为0.15mm时的位移和频谱;图5c所示是转速为13 000r/min、轴向切深1mm、径向切深6mm、每齿进给量为0.15mm时的位移;图5d所示是转速为13 000r/min、轴向切深1mm、径向切深8mm、每齿进给量为0.15mm时的位移。从中不难看出径向切深对切削的影响较小,在很大的变化范围内,切削质量都较好,从图5b的频谱结构可以看出颤振频率在某个固有频率附近[4]。

图5 径向切深对颤振的影响

2.3 每齿进给量对颤振的影响

在初始位移为 0.01mm、模态参数刚度为3.0725×107N/mm、阻尼系数为0.031152、固有频率为3754.2H z的情况下,每齿进给量对颤振的影响见图6,其中,图6a、6b所示分别是转速为13 000r/m in、轴向切深 6mm、径向切深1mm、每齿进给量为0.5mm时的位移和频谱;图6c所示是转速为13 000r/m in、轴向切深6mm、径向切深1mm、每齿进给量为0.2mm时的位移。从图6中可以看出,每齿进给量对铣削加工影响极大,应谨慎选用每齿进给量。从频谱结构图可以看出,颤振频率为3700Hz,在固有频率3754.2Hz附近,与已有的研究结果一致[1,4]。

图6 每齿进给量对颤振的影响

2.4 轴向切深对颤振的影响

在初始位移为 0.01mm、刚度为3.0725×107N/mm、阻尼系数为0.031 152、固有频率为3754.2Hz的情况下,轴向切深对颤振的影响见图7,其中,图7a所示是转速为12 000r/m in、轴向切深1mm、径向切深1mm,每齿进给量为0.15mm时的位移;图7b所示是转速为12 000r/m in、轴向切深 2.5mm、径向切深 1mm、每齿进给量为0.15mm时的位移;图 7c所示是转速为12 000r/min、轴向切深8mm、径向切深1mm、每齿进给量为0.15mm时的位移;图7d(初始位移为0.5mm)仅初始条件不同于图7c,铣削是失稳的。从中可以看出对不同的轴向切深有不同的稳态振幅和稳态频率,从而有不同的加工精度。从模态参数算得该系统的阻尼为1469.6N◦s/mm,从切削力的时间部分可以看出,即便它起到负阻尼的作用,整个系统也还是阻尼很大的状态并且切削力还是动态变化的,故系统在较小冲击下是稳定的,较大冲击下系统就失稳了,这反映了系统对初始条件的敏感性,体现了系统的非线性特性。一般的线性系统最终是稳定在一个固定值,但从图7中看出它的终态是一个周期性振动。

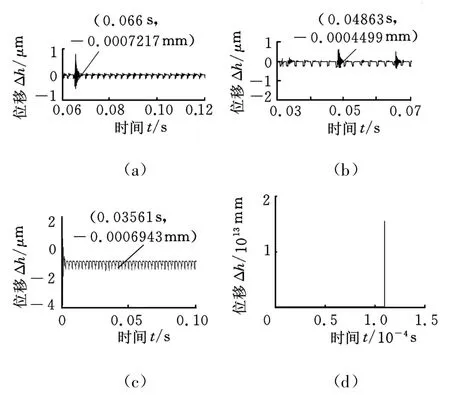
图7 轴向切深对颤振的影响

2.5 速度对颤振的影响

在初始位移为 0.01mm、刚度为3.0725×107N/mm、阻尼系数为0.031 152,固有频率为3754.2H z的情况下,速度对颤振的影响见图8,其中,图 8a、图 8b所示分别是转速为12 000r/min、轴向切深6mm、径向切深2mm、每齿进给量为0.15mm时的位移和频谱;图8c所示是转速为13 000r/m in、轴向切深6mm、径向切深2mm、每齿进给量为0.2mm时的位移;图8d所示是转速为13 500r/min、轴向切深6mm 、径向切深2mm、每齿进给量为0.15mm时的位移;图8e所示是转速为9000r/min、轴向切深6mm、径向切深2mm、每齿进给量为0.15mm时的位移。从图8的稳态振幅可以看出,在12 000r/m in和13 500r/m in附近铣削的质量较好,这与稳定性叶瓣图相符合;从2.2和2.4的结果知道,此时的轴向切深较大,加工质量较差,再一次反映了轴向切深是对铣削加工影响很大的参数。

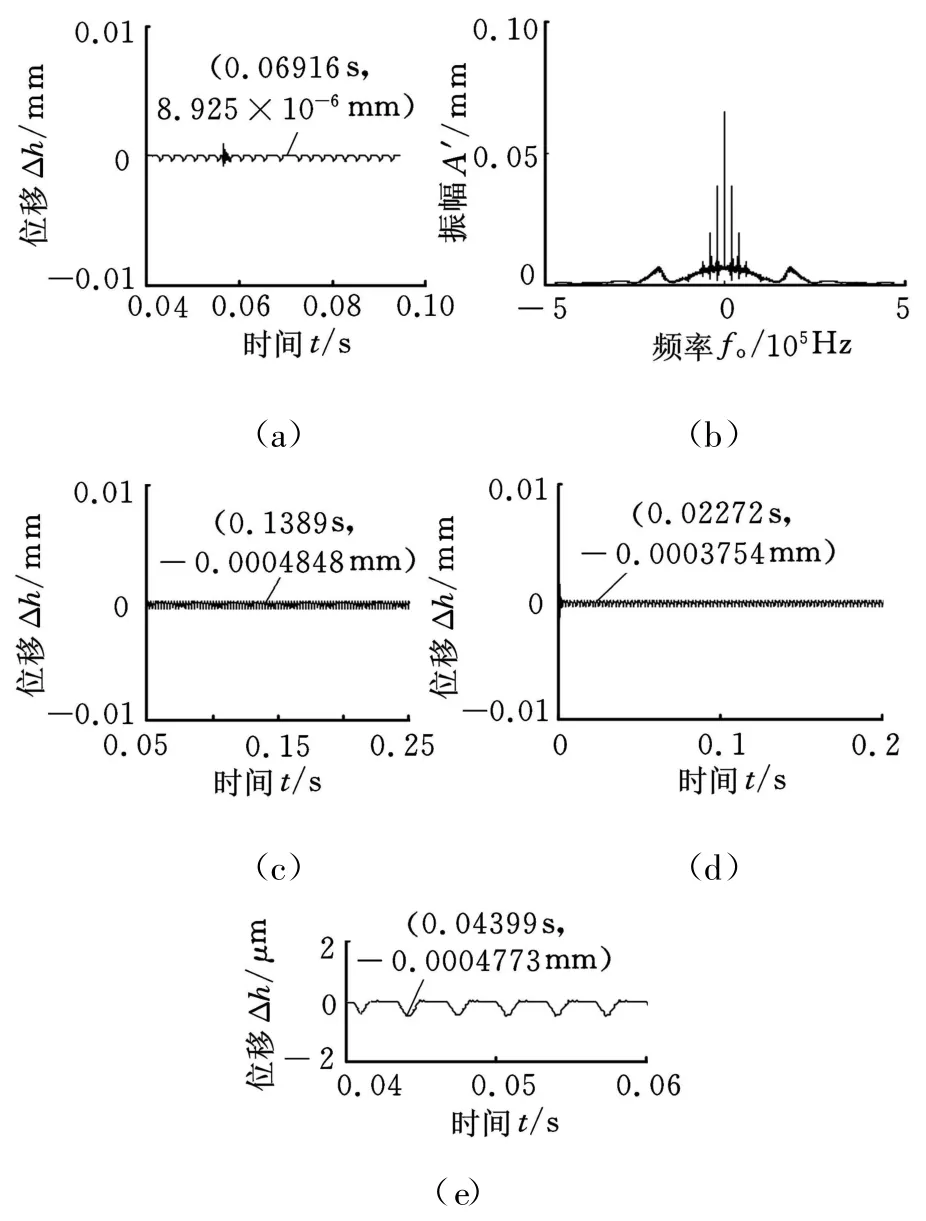
图8 速度对颤振的影响

2.6 径向切深与轴向切深的非线性关系和轴向切深与进给量的关系

从2.2节可知,径向切深在很大范围内变化,切削过程的动态特性基本不变,又从2.4节知道轴向切深对铣削影响很显著,由径向切深与轴向切深的非线性关系可以得出,在实际加工预测过程中,可通过对系统工况的估计得出模态参数,然后进行仿真预测得出最佳参数组合。从2.3节知道每齿进给量对铣削的影响非常显著,稍微变动就可对加工质量造成很大影响,因此,轴向切深与每齿进给量以及径向向切深与每齿进给量的关系都是很复杂的。至于螺旋角的影响,由于文献[9]作了研究,本文从略,从图3和图4可以得出增大螺旋角确实改善了铣削的加工断续性。

3 动态切削实验验证[10]

动态切削实验中,机床采用Mikron公司的UCP DURO800Duro五坐标高速加工中心;工件材料选用 2A 12铝合金(T8状态);刀具使用Fraisa硬质合金立铣刀,刀尖圆角半径为1.5mm,螺旋角300°,刀具直径12mm,两齿;传感器选用WD3005型电涡流位移传感器,转换系数为6.6V/mm,采样频率取为20kH z;数据采集仪采用NIUSB 9223 24位专用数据信号采集系统。实验参数如下:轴向切深a p(mm)、径向切深 a e(mm)、每齿进给量 fz(mm)、转速n(r/min)。

预先制作多块100mm×50mm×45mm的试件,每次装夹都保证工件处于虎钳的相同位置。实验结果见图9、图10。图9所示为轴向切深对铣削的影响,与2.4节趋势一致,至于幅值上的出入是由于仿真中仅采用某阶模态参数,而实际的振动过程是很多模态在起作用而造成的,把各阶模态的响应叠加起来,幅值就相近了。图10所示为径向轴向切深对铣削的影响,也与2.2节中的结果相符,图10中可以看出径向切深变化很大时,振幅变化不过0.8μm左右。

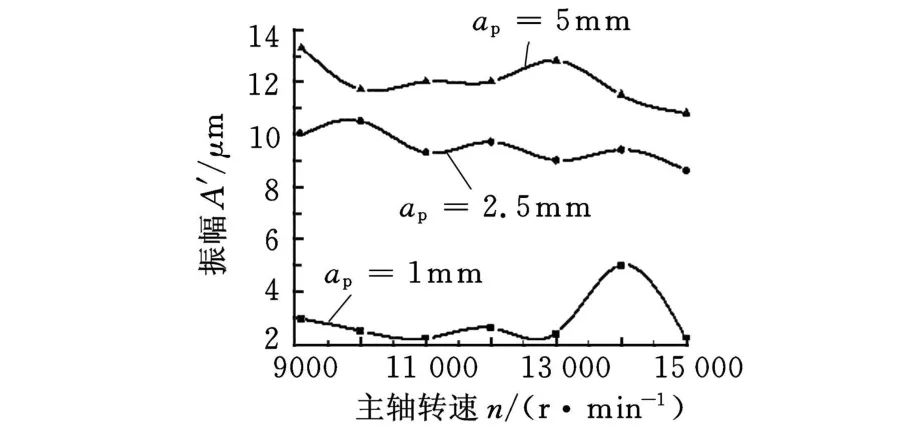
图9 轴向切深对铣削的影响

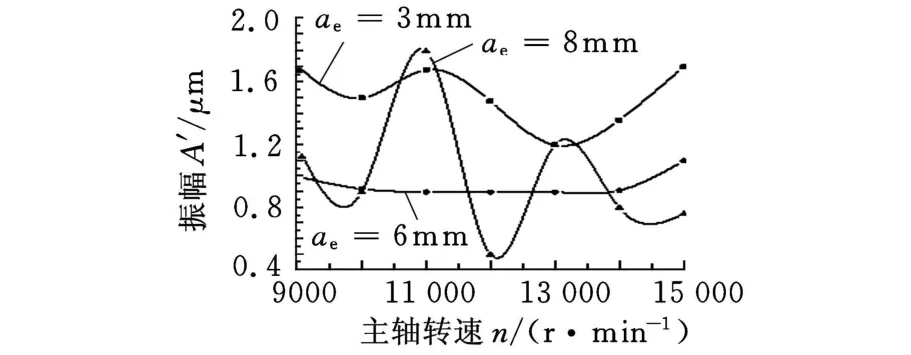
图10 径向轴向切深对铣削的影响

4 结语

据上面分析得出:颤振受每齿进给量、径向切深、轴向切深、螺旋角和转速的影响,通过选择合适的切削用量,铣削的断续性和其他非线性因素带来的不利影响是可以抑制的,铣削可以达到很高的精度;从转速与位移的关系可看出在一定范围内转速有很大的选择余地。从径向切深与轴向切深的关系看,两者的不同组合会有不同的加工质量,在一定的转速下,增大径向切深,切削过程更稳定,加工质量更高,这为切削加工产品质量控制的预测提供了可能。

[1] A ltinas Y.数控技术与制造自动化[M].罗学科,译.北京:化学工业出版社,2002.

[2] Budak E,A ltintas Y.Analy tical Prediction of Chatter Stability M illing[J].Part 1:General Formu lation.Dynam ic System s and Control Division,1995,57(1):545-556.

[3] A ltintas Y.Manu facturing Automation-metal Cutting Mechanics,Machine Tool Vibration and CNC Design[M].Cambridge:Cambridge University Press,2000.

[4] 师汉民.金属切削理论及其应用新探[M].武汉:华中科技大学出版社,2003.

[5] 王延忠,周元子,刘强,等.基于 ABAQUS的龙门五面加工中心动态特性分析[J].机床与液压制造,2008,36(2):3-4,40.

[6] 刘习军,陈予恕.机床速度型切削颤振的非线性研究[J].振动与冲击,1995(2):5-10.

[7] 罗玉军,高尚晗,高中庸.动态切削力对切削颤振的影响[J].机械设计与制造,2007,11:200-202.

[8] Li Zhongqun,Liu Qiang.So lution and Analysis o f Chatter Stability for End M illing in the Time-domain[J].Chinese Journal of Aeronautics,2008,21:169-178.

[9] Song Q inghua,A i Xing,W an Y i,et al.Influence o f the Too l Helix Angle on the Stability in H ighspeed M illing Process[J].Transactions of Nanjing University of Aeronautics&Astronautics,2008,25(1):18-25.

[10] 汪通悦,何宁,李亮,等.薄壁零件高速铣削振动影响因素研究[J].淮阴工学院学报,2009,18(1):13-17.

Chatter Analysis on Non-linear Time and Frequency Domain in Finishing M illing Processes

Fang Xifeng1Tong Yonghai1Wu Chunqiao1Zhang Shengwen1Wang Tongyue2
1.Jiangsu University of Science&Technology,Zhen jiang,Jiangsu,212003
2.Industry College o f Huaiyin,Huai'an,Jiangsu,223001

To restrain the chatter in finishingmilling processes,adoptingmany non-linear factors which are difficult to modelin any closed-form m athematicalmodel,a non-smooth non-linear variable coefficient differential equation in time and frequency domain was established and the numerical solution of the equation w as obtained.The im pact of the cutting parameters and helix angle on the chatter was p roposed.The relationship between the radial cutting dep th and the axial depth and the impact of the feed rate on the axial dep th were obtained,which were validated by experiments.

chatter;finishing milling;non-linear;cutting parameter

TH 164;TG501

1004—132X(2011)05—0541—05

2010—02—07

江苏省高校自然科学基金资助项目(09KJB460003);江苏省重点实验室开放基金资助项目(HGDM L-0809,HGDM L-0801,CJ0905);江苏省普通高校研究生科研创新计划资助项目

(编辑 袁兴玲)

方喜峰,男,1971年生。江苏科技大学机械工程学院副教授、博士后研究人员。主要研究方向为智能设计与制造、数控加工技术等。获市级科技三等奖1项。发表论文20余篇。仝永海,男,1980年生。江苏科技大学机械工程学院硕士研究生。吴春桥,男,1984年生。江苏科技大学机械工程学院硕士研究生。张胜文,男,1963年生。江苏科技大学机械工程学院教授。汪通悦,男,1966年生。淮阴工学院江苏省数字化设计制造技术重点实验室副教授。