浮吊船-吊物耦合矢量建模

张梁娟 朱昌明 包继虎 张 鹏

上海交通大学,上海,200240

浮吊船-吊物耦合矢量建模

张梁娟 朱昌明 包继虎 张 鹏

上海交通大学,上海,200240

以海上风力发电机安装为研究背景,基于矢量动力学理论,建立了9自由度的浮吊船-吊物耦合的非线性动力学模型。模型将船体简化为刚体,以其在风浪流等载荷激励下的6自由度运动为基础,引入浮吊船和吊物的耦合作用,且吊物的耦合作用通过其对船体施加的力和力矩体现。模型同时考虑了风机吊物摆动过程中吊索的弹性变形因素以及吊索的升降作业操作等因素。该模型采用了向量和矩阵记法,具有很强的适用性和通用性。最后在同等设定条件下与以往的研究模型进行了比较,比较结果验证了该模型的有效性。

浮吊船;起重船;吊装;矢量法;耦合作用

0 引言

浮吊船是海上风电场建设中不可缺少的运输和吊装工具,是保证海上风机顺利安装的重要设备之一。在吊装对接过程中,浮吊船和吊物系统的动态响应对安装是否能够顺利进行有着重要的影响,而浮吊船以及吊物系统的动态响应不仅受到风浪流载荷、锚泊系统的影响,还需要考虑浮吊船和吊物之间的耦合作用,系统整体的运动具有很强的非线性特征,建立正确的浮吊船-吊物耦合模型,是进一步提高吊装性能并保证风机顺利安装的前提。

对于海上吊物系统,很多学者进行了建模和实验研究。以往的模型大部分忽略船体和吊物之间的耦合作用,把系统简化为一个空间球摆[1-6],把船体在波浪中的运动引起的吊臂顶端的运动作为系统的输入。但是对于海上风机安装工程背景来说,风机组件的总重达到750t,且安装过程中所能承受的加速度不能超过0.25g,以往建模方法不仅无法描述船体和吊物系统的耦合作用,而且不能详尽描述风浪载荷、锚泊系统等外界载荷对系统的直接影响。Daqaq[7]、Idres等[8]以及Schaub[9]分别研究了浮式回转起重机的吊装模型,他们建立了8自由度的船体吊物模型,引入了波浪载荷等环境因素,考虑了起重机吊臂的旋转以及和船体的耦合作用,但是他们都忽略了吊索的弹性变形因素。在前人研究的基础上,本文以海上风机安装情况为背景,考虑了吊索的弹性变形,借助于动量和动量矩定理,导出系统在吊装过程中的数学方程组,从而有助于后续对浮吊船和吊物系统的动态响应以及吊索张力的研究分析。

1 参考坐标系

为了研究船体及吊物的运动和受力情况,必须建立合理的参考坐标系。由于浮吊船是锚泊作业,不具有固定航速和航向,故可以认为其运动是围绕初始平衡位置的摇荡运动,建立的两种坐标系如图1所示,O0XYZ为固定坐标系,O0为原点,可以取地面上或海面上任何一点,Z轴指向地心,X轴和Y轴相互垂直且在水平面内。坐标系O0 XYZ也是一个惯性坐标系,用 Г表示,I、J、K分别表示固定坐标系三轴的单位矢量。固定坐标系虽然是惯性参考系,但在研究船与周围海水间的相互作用力时,由于水动力等载荷决定于船体与海水的相对运动,用固定坐标系参数来表达较困难,因此为了方便计算海洋环境载荷,需要在船体坐标系下建立模型。船体坐标系Oxyz的原点O可以取在船体上任何一点,针对具体问题,这里取O点为船体的几何中心。纵轴 x指向初始平衡位置时船体的体首,横轴y指向初始平衡位置时船体的右舷,垂直轴z指向初始平衡位置时船体底部,船体坐标系固定在船体上,且认为其初始平面与静水面重合,用 И表示,i、j、k分别表示船体坐标系三轴的单位矢量,且用eИ表示这一组矢量基。定义船体沿三个船体坐标轴的运动分别为纵荡x、横荡y和升沉z,绕三个坐标轴的转动分别为横摇φ、纵摇θ和首摇ψ。

图1中虚线部分为浮吊船和起重机吊臂的结构示意图,A点为起重机吊臂端点,B点表示吊物点。G点为船体的质心。A′为A点在xy平面内的投影,即AA′平行于z轴。定义OAA′三点构成的平面为吊臂平面。B′为B在吊臂平面内的投影,α和β分别为面内角和面外角。

2 船体动力学方程

如图1所示,r O为船体坐标系原点O点与固定坐标系O0点之间的位置矢量,rAO为吊臂端点A与船体坐标系原点O点之间的位置矢量;r BO表示吊物点B与船体坐标系原点O点间的位置矢量,rBA表示吊物点B与吊臂端点A点间的位置矢量,则船体相对于固定坐标系的速度矢量v O可以表示为

根据动量定理及矢量求导法则,推出船体平移运动的方程:

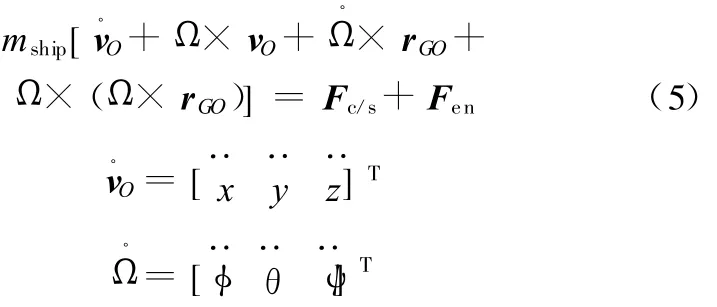
式中,Fc/s为吊物系统对船体的耦合作用力;Fen为环境载荷作用力,主要包括风、浪、流等环境扰动对船体的作用力、水动力载荷以及锚泊系统作用力等。

由上面分析知,动量 H作用线通过船体重心,则动量H对原点的矩L H为

式中,JG为船体对原点在重心的坐标系的惯量矩阵;J的物理意义为船体对原点的总惯量矩。

根据动量矩定理和矢量求导法则,可以推出:

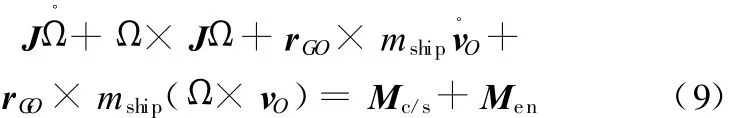
式中,Mc/s为吊物对船体的作用力矩;Men为环境载荷对船体的作用力矩。

根据以上推导,船体的运动可以由式(5)和式(9)矢量叉乘形式方程确定。吊物与船体的耦合作用通过吊物系统对船体的作用力和作用力矩来体现。

3 吊物系统动力学方程

3.1 吊物系统模型建立

对于吊物来说,当不考虑空气等环境阻尼的影响时,下面方程成立:

式中,FT为吊索作用于风机吊物上的张力;m为风机吊物质量;aB为吊物加速度矢量。从而推出:

式中,lR为任意时刻吊索的长度,考虑吊索的弹性变形,其长度由两部分组成,即 lR=l+r,其中,l为由放绳操作决定的吊索长度,r为任意时刻的吊索的弹性伸长量。

沿船体坐标系三轴投影得到F c/s在该矢量基上的坐标阵:

3.2 吊物摆角方程

在一般情况下,普遍认为吊索张力总是沿着吊索轴向方向的。为了获得吊索张力沿吊索轴向以及法向的分量表达式,首先将船体坐标基矢量eИ绕j转过α角,得到一组新的过渡基,用eU表示;然后eU绕新的i′转过β角,得到新的一组单位正交矢量系 er,其基矢量分别用 i″、j″、k″表示 ,其中k″沿着吊索方向,i″、j″分别垂直于吊索方向,如图2所示。

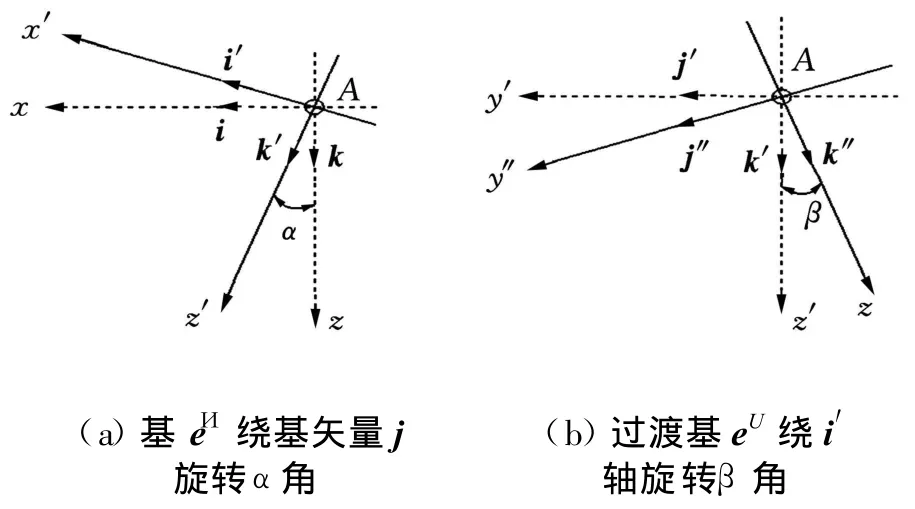
图2 坐标旋转

将吊索张力在基er下展开,考虑吊索的弹性变形,且这里假定吊索的弹性系数为kr,则有

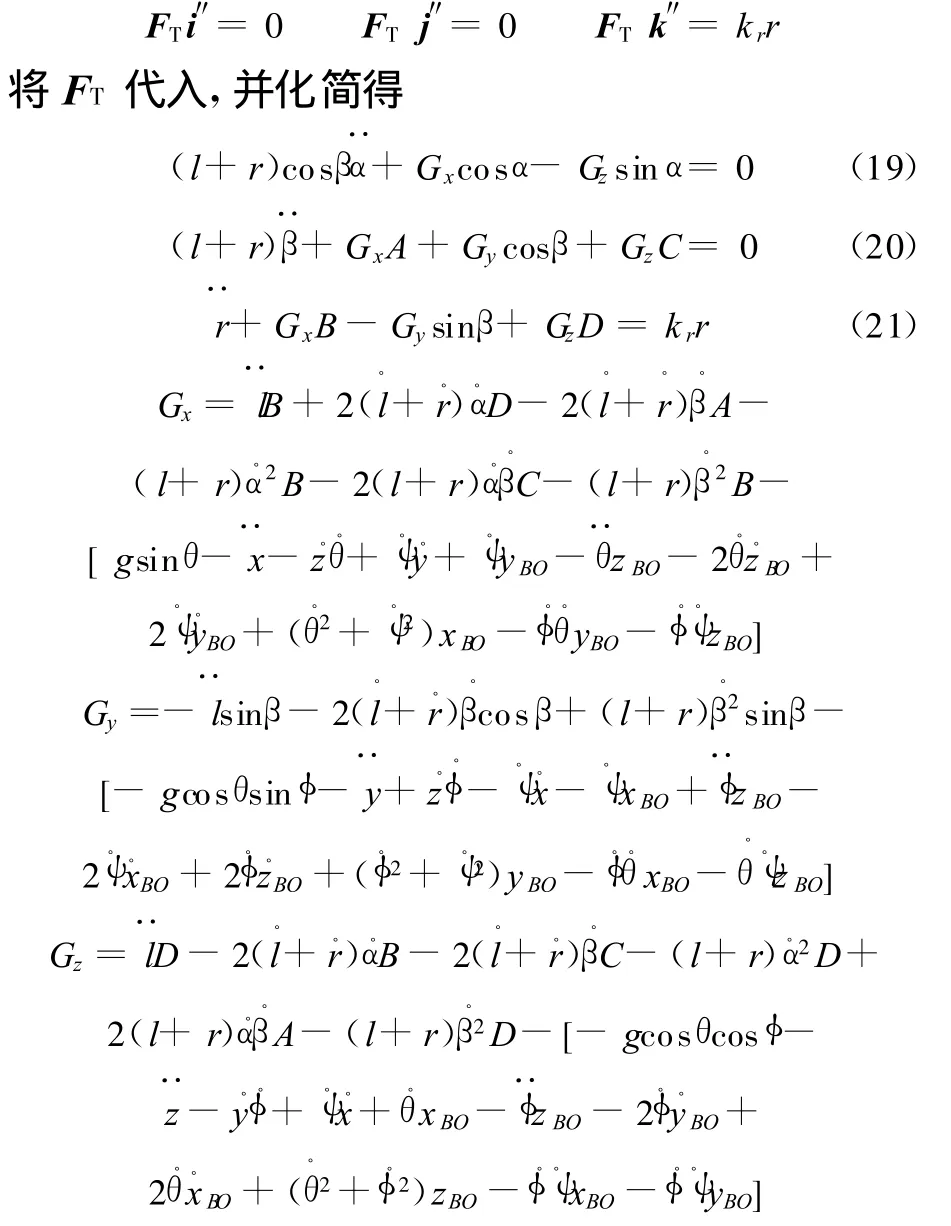
其中 ,A=sinαsinβ,B=sinαcosβ,C=cosαsinβ,D=cosαcosβ。联立式(5)、式(9)、式(19)～式(21),从而可以获得浮吊船-吊物耦合的动力学方程组。

4 模型有效性验证

4.1 船体模型验证

将船体动力学方程式(5)和式(9)分别在船体坐标系下展开,即将各个向量向船体坐标系的三个坐标轴投影,可得

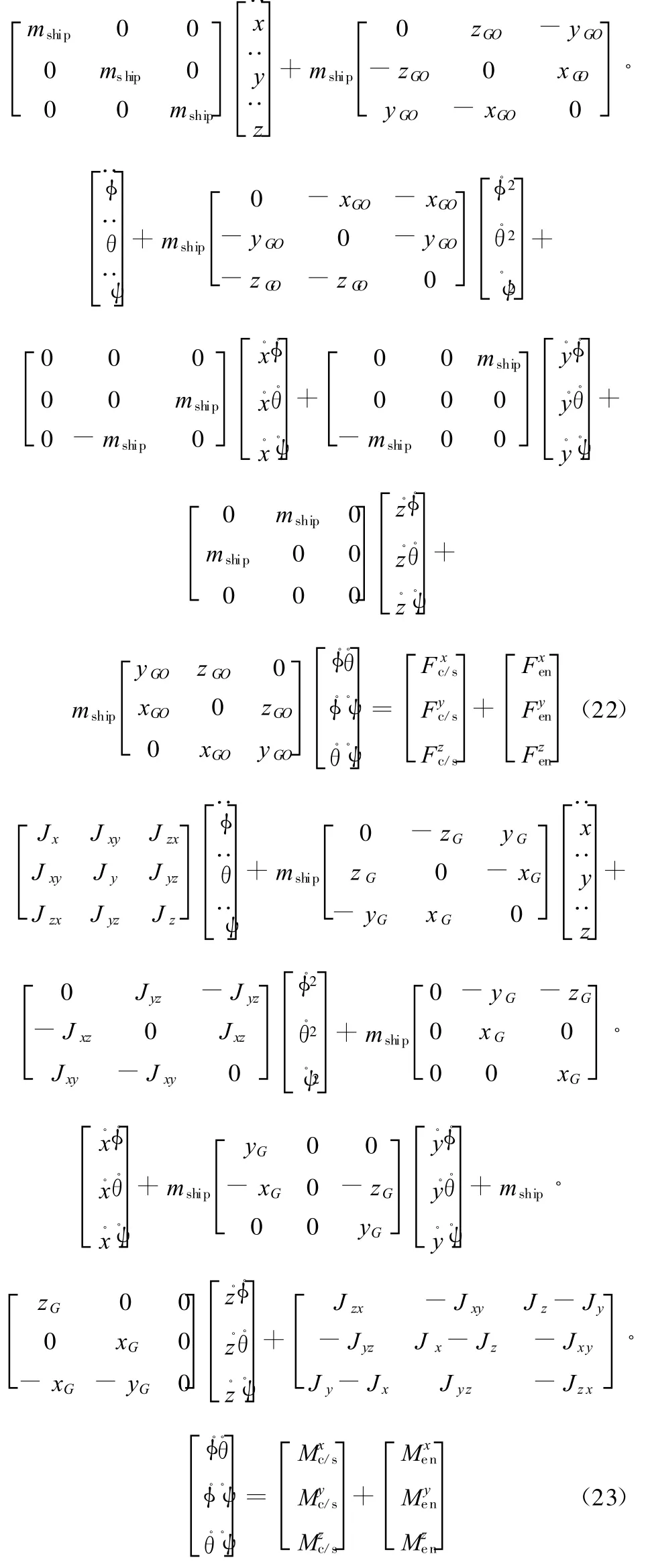
式中,xG、yG、zG为重心G到船体坐标系原点O点的位置矢量在船体坐标系的三个坐标轴的投影;Jx、Jy、Jz分别为船体绕x、y、z轴的转动惯量;Jxy、Jyz、Jzx分别为船体绕x 、y轴,y、z轴和z、x轴的惯量积;右上标 x、y、z分别表示在各个坐标轴上的投影分量。

式(22)和式(23)中的速度平方项以及耦合乘积项的产生是由船体坐标系相对于固定坐标系运动而产生的。如果认为船体的摆荡运动是微幅的,则可以将上述方程可以简化为

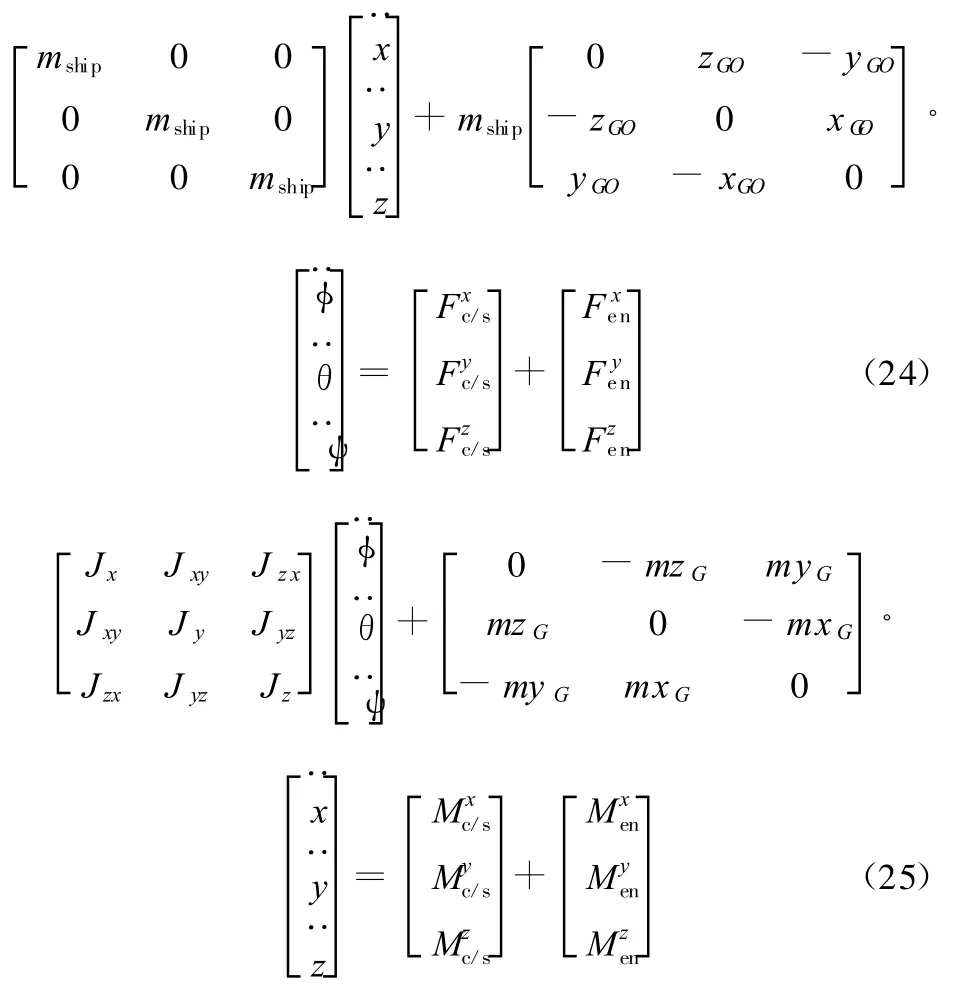
此时得到的船体运动模型与Schellin等[10]曾经研究过的模型是一致的。

4.2 吊物系统模型验证

此即文献[3]曾经研究过的吊物系统摆振模型。而在文献[3]中,M asoud等学者在三自由度运动平台上通过T-ACS船的1/24比例模型对该模型进行了有效的验证。由此可见,本文的模型在设定条件下可以推导出文献[3]的研究模型。

5 结论

(1)考虑了船体和吊物系统的耦合作用,且该作用通过吊物对船体的作用力和作用力矩体现。

(2)不再将船体运动简单的处理为6个方向上的简谐运动,也不作为系统的已知运动输入量,而是从海洋环境载荷出发,船体6自由度的运动同样作为系统未知量,使得整个模型可以考虑的因素更多,如吊装作业中锚泊系统的影响等。

(3)模型方程采用矢量和矩阵表达,具有很强的通用性。为了方便计算水动力等环境载荷,可将方程在船体坐标系下展开,即把各个矢量向船体坐标系的三个坐标轴投影,获得在船体坐标系下的耦合模型方程组。

(4)与以往的有效模型进行了比较,比较结果表明本文建立的模型考虑的因素更多,形式更通用。

(5)在进行浮吊船-吊物耦合系统在海面上的动态特性的研究时,不仅需要建立上述数学模型,还要求计算风浪流等环境干扰力、流体作用力以及锚泊力等外部载荷。由于篇幅的限制,以上只是针对浮吊船-吊物系统的数学模型进行了研究和讨论,而对该系统承受的外界载荷的计算以及整个系统的动态响应分析将在日后的工作中补充进来,从而实现对这样一个复杂的动力学系统的完整描述。

[1] Todd M D,Vohra S T,Leban F.Dynam ical Measurements of Ship Crane Load Pendulation[C]//Oceans 97.M TS/IEEE Conference Proceedings.H alifax,NS,1997:1230-1236.

[2] Chin C M,Nay feh A H,Mook D T.Dynam ics and Control of Ship-mounted Cranes[J].Journalof V ibration and Contro l,2001,7(6):891-904.

[3] Masoud ZN,Nayfeh A H,M ook D T.Cargo Pendulation Reduction o f Ship-mounted Cranes[J].Nonlinear Dynam ics,2004,35(3):299-311.

[4] Elling R,M cClinton A.Dynamic Loading of Shipboard C ranes[C]//Ocean 73,IEEE International Conference on Engineering in the Ocean Environment.New York,1973:74-177.

[5] Eihab M A R,Nay feh A H,Masoud Z N.Dynam ics and Control of Cranes:A Review[J].Journa lof V ibration and Contro l,2003,9(7):863-908.

[6] SpathopoulosM P,Fragopoulos D.Pendulation Control of an O ffshore Crane[J].International Journal of Control,2004,77(7):654-670.

[7] Daqaq M F.V irtua l Reality Simulation of Ships and Ship-Mounted C ranes[D].Blacksburg,Virginia:V irginia Polytechnic Institute and State University,2003.

[8] Idres M M,Youssef K S,Mook D T,et al.A Nonlinear 8-DOFCoupled C rane-ship Dynamic Model[C]//44thA IAA/ASME/ASCE/AHS Structures,Structural Dynam ics,and M ateria ls Con ference.Norfolk,V irginia,2003:1-5.

[9] Schaub H.Rate-based Ship-mounted Crane Payload Pendu lation Contro l System[J].Contro l Engineering Practice,2008,16(1):132-145.

[10] Schellin T E,Jiang T,Sharma S D.Crane Ship Response to Wave G roups[J].Journal of Offshore M echanics and A rctic Engineering,1991,113(21):1-2.

Coup ling Vector Modeling of Floating Crane and Suspended Load

Zhang Liangjuan Zhu Changming Bao Jihu Zhang Peng
Shanghai Jiaotong University,Shanghai,200240

A 9-DOF nonlinear dynamicsmodel was set up in the background of offshore turbine installation.The dynam ics m odel incorporated ship motions coup led w ith non linear large payload sw ings.The ship and cranew ere treated as one rigid body and themodel included arbitrary,bi-angu lar sw ings of the suspended load coup led with the 6-DOF of the ship,in addition to 3-DOF of the load in-plane and out-of-plane sway angles and elastic stretch of the hoisting cable.The model was described by matrix and vector,which is very general and applicable.The validity of the model was verified by com parion w ith existingmodels.

floating crane;crane ship;heavy lift;vectormechanics;coup ling

TP391.9

1004—132X(2011)05—0561—05

2010—03—01

(编辑 袁兴玲)

张梁娟,女,1983年生。上海交通大学机械与动力工程学院博士研究生。主要研究方向为物流装备动力学。获发明专利2项,发表论文10余篇。朱昌明,男,1951年生。上海交通大学机械与动力工程学院研究员、博士研究生导师。包继虎,男,1977年生。上海交通大学机械与动力工程学院博士研究生。张 鹏,男,1978年生。上海交通大学机械与动力工程学院讲师、博士后研究人员。