基于多目标优化的AGV驱动系统模型辨识

武 星 楼佩煌 唐敦兵

南京航空航天大学，南京，210016

基于多目标优化的AGV驱动系统模型辨识

武 星 楼佩煌 唐敦兵

南京航空航天大学，南京，210016

以自动导引车（AGV）的驱动系统为对象，提出了一种基于最小二乘法和多目标遗传算法的新型模型辨识方法。以最小二乘法的辨识模型为多目标遗传算法的进化导师，选择具有多指标均衡优化性能的个体为精英，利用无损有限精度法保持种群多样性，设计多指标聚合函数快速搜索Pareto最优解。AGV驱动系统的模型辨识试验表明，该方法辨识的模型响应曲线在幅值和相位两方面皆与对象响应曲线较为吻合，研究结果可为AGV伺服控制系统的设计提供较为精确的系统模型。

自动导引车；模型辨识；遗传算法；多目标优化

0 引言

在自动导引车（AGV）运动控制研究中，较普遍的系统建模方法是动力学分析法［1］，有时也采用电机的一阶模型代替驱动系统的动态模型［2］，然而前者面临难以测量惯性参数和难以对动静态摩擦项进行建模等问题，而后者采用的简单模型与实际误差较大。为在AGV路径跟踪［3］中提供足够的纠偏控制量，必须根据驱动系统的执行能力设计伺服控制器，因此，获取精确的驱动系统模型是一个首要问题。

以最小二乘法为代表的经典辨识方法已发展得相当成熟，但也存在着多方面的局限性。在将系统到模型的映射问题转化为辨识精度的优化问题时，可考虑以遗传算法（GA）为代表的智能优化方法［4－5］。传统遗传算法的适应度计算是针对单目标的，在解决复杂问题时容易出现种群早熟现象。Fonseca等［6］提出的Pareto最优概念奠定了多目标遗传算法（MOGA）的基础，Leung［7］采用多个适应度函数并行搜索解空间，Deb等［8］提出一种带精英策略的快速非支配排序遗传算法（NSGA－Ⅱ），这些研究主要通过提高种群多样性来避免早熟现象。同时，在进化过程中，为避免丢失已获得的优良个体，NSGA－Ⅱ还采用了精英保留策略。

本文为AGV驱动系统提出一种基于多目标优化的新型模型辨识方法，先采用最小二乘法选择具有多指标均衡优化性能的个体，再通过多目标遗传算法快速搜索Pareto最优解。该方法可获得幅值精度和相位精度俱佳的驱动系统模型。

1 AGV工业样机及试验系统

本文的研究对象为一台采用视觉导航的AGV工业样机，如图1所示。该样机的车体尺寸为1.9m×0.9m，有效载荷为5kN。驱动系统采用差速转向方式，两驱动轮对称安装于车体左右两侧，分别通过两套直流伺服装置独立控制驱动轮的转速和方向；自由轮安装于车体前后两方，仅起支承作用。

图1 AGV工业样机

车载控制器采用自主设计开发的嵌入式控制系统，基于嵌入式微控制器ARM和实时操作系统μC／OS－Ⅱ设计了路径跟踪控制器和速度伺服控制器，前者针对路径偏差计算驱动轮的目标速度，后者根据目标速度和编码器反馈的实际速度，通过伺服控制消除速度误差。对工业样机的重载驱动系统，由于惯性参数和各类摩擦项难以确定，根据简化理论模型设计的PID控制器效果不佳，因此，本文希望通过研究驱动系统的模型辨识，为设计高性能的伺服控制器打下良好的基础。

试验系统包括AGV车载系统和主控计算机，两者通过无线通信装置相连。主控计算机在Windows操作系统下设计开发了一个包含数据库的AGV远程控制软件，将车载控制器检测的驱动轮实时速度通过无线方式传输到主控计算机并保存，从而获取驱动系统的阶跃响应曲线，以比较各种模型辨识方法的优劣。

2 传统模型辨识方法及缺陷

采用上述AGV试验系统进行阶跃响应试验，驱动系统的对象响应曲线如图2中的点线所示。根据该试验数据，利用最小二乘法（LSM）辨识驱动系统的二阶、四阶和六阶模型，相应的模型响应曲线如图2所示。其中，六阶模型的响应曲线与对象响应曲线的逼近程度最高，但高阶模型的控制器设计比较复杂，通常简化为二阶模型，而LSM辨识的二阶模型与对象响应曲线具有较大的幅值误差，因此，下面采用遗传算法辨识驱动系统的二阶模型。

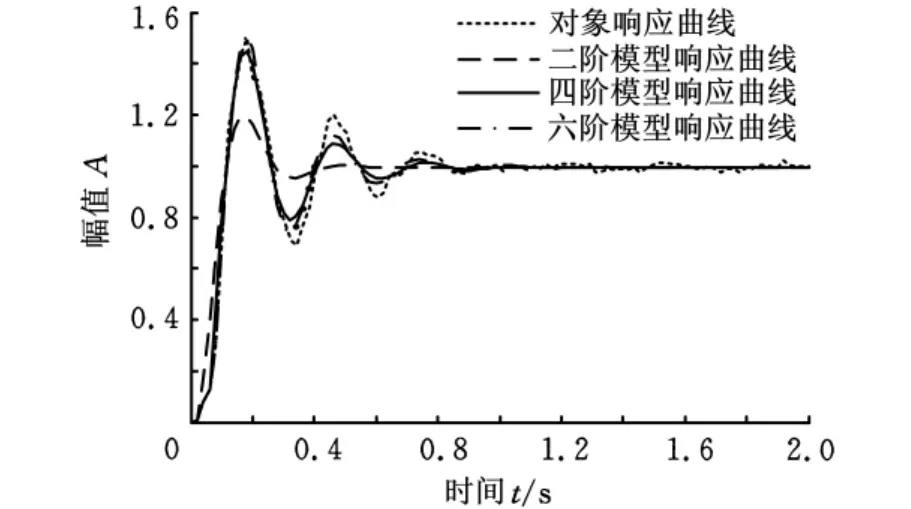
图2 LSM辨识的模型响应曲线

假设驱动系统的理想二阶模型为

在遗传算法中，优化目标是使模型响应曲线尽量逼近对象响应曲线。考虑到驱动系统前期迅速变化的响应曲线，采用ISTE型目标函数，并确定适应度函数，如下所示：

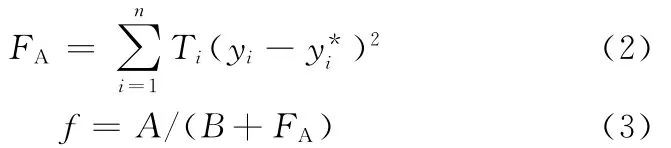
式中，FA为目标函数；yi、y＊i分别为采样时刻Ti的模型响应输出和对象响应输出；f为适应度函数；A为调节适应度大小的正常数；B为避免分母为零的微小正常数。

根据系统模型的阶次和试验数据的数目，设置遗传算法的种群规模N＝60，进化代数G＝100。先采用单目标传统型遗传算法（SCGA）进行辨识，设置交叉概率Pc＝0.6，变异概率Pm＝0.2，经过5次随机试验，辨识的模型参数如表1所示。其中，第1次辨识模型的适应度最大，第5次辨识模型的适应度最小，第3次辨识模型与最小二乘法的结果比较接近，5次辨识模型的适应度平均值为2.4899，均方差为0.3869。由图3可见，第1次辨识模型的幅值精度明显优于LSM辨识的模型，然而从第二个波峰位置开始还是出现较大的相位误差。

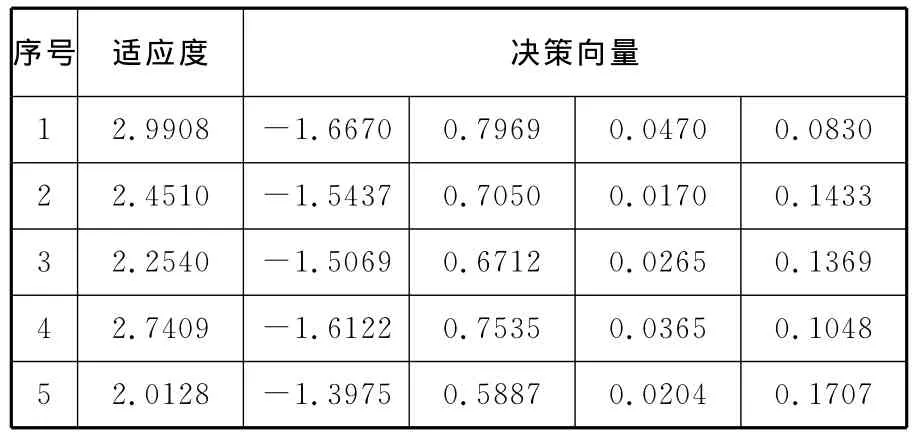
表1 SCGA辨识的模型参数

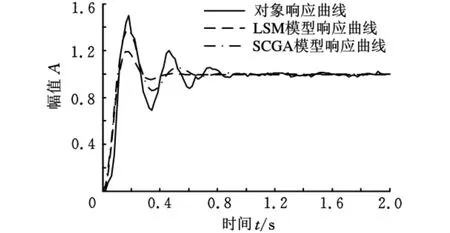
图3 SCGA辨识的模型响应曲线

下面再采用单目标自适应遗传算法（SAGA）［9］对试验数据进行模型辨识，适应度函数、种群规模、进化代数保持不变，交叉和变异等遗传操作与文献［9］相同。经过5次随机试验，辨识的模型参数如表2所示。其中，第5次辨识模型的适应度最大，比SCGA的第1次有很大提高；第2次辨识模型的适应度最小，略优于SCGA的第5次辨识模型的适应度。5次辨识模型的适应度平均值为2.9417，比SCGA的平均值有较大提高，均方差为0.6797，也大于SCGA的均方差。可见，SAGA的探测能力优于SCGA的探测能力，最优辨识模型比SCGA具有更好的适应度，然而SAGA的收敛能力相对较差，每次辨识结果有较大差异。

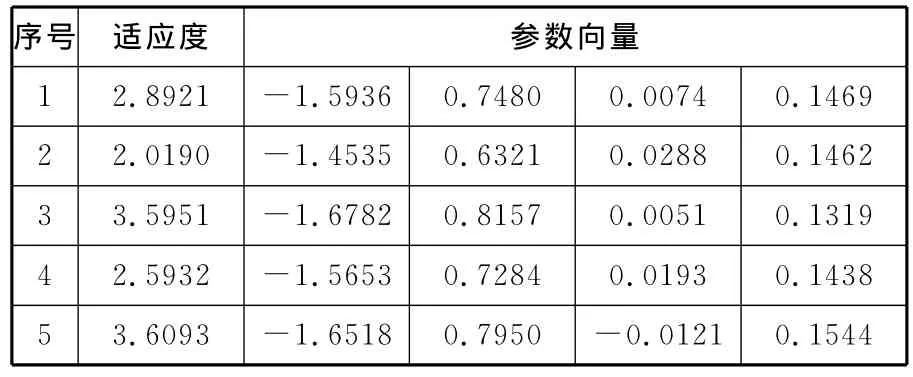
表2 SAGA辨识的模型参数

在图4中，点划线表示第5次辨识模型的阶跃响应曲线，与图3相比，该曲线在第一个波峰位置的幅值误差以及第二个波峰位置的相位和幅值误差都略有改善，但改善程度远不及适应度提高的程度。图3和图4都具有一个共同特点，SAGA模型响应曲线从第二个波峰位置开始出现较大的相位误差，效果不如LSM辨识的系统模型。这些试验现象说明遗传算法的目标函数没能全面反映模型辨识的优化目标。

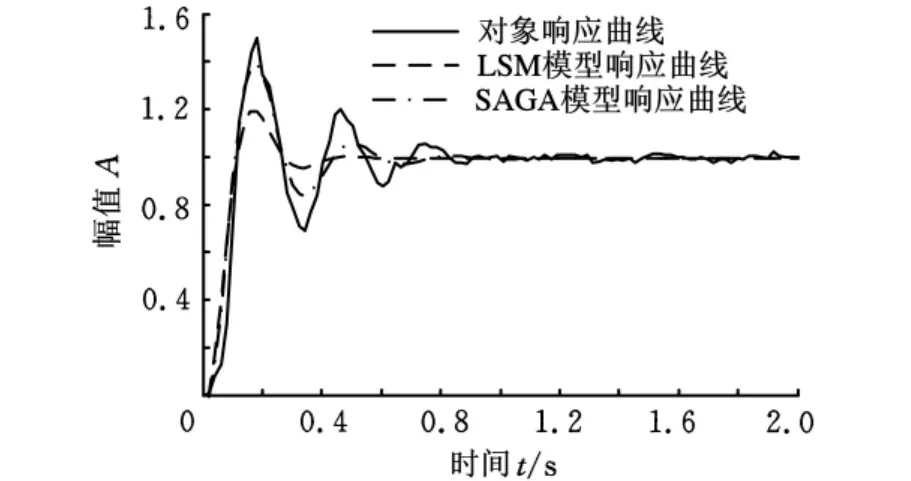
图4 SAGA辨识的模型响应曲线

目标函数式（2）描述的是对象响应输出与模型响应输出之间的幅值误差。对于理想响应曲线，最小化幅值误差也可同时保证相位误差最小；然而对于实际响应曲线，由于各种失真因素的存在，模型响应输出的幅值误差和相位误差可能无法同时最小化，多个优化目标之间存在相互制约的关系，仅考虑幅值误差的目标函数式（2）必然导致单目标遗传算法的相位精度不足。

3 基于多目标优化的AGV模型辨识方法及其试验

针对传统模型辨识方法存在的缺陷，在目标函数中增加相位误差的定义：

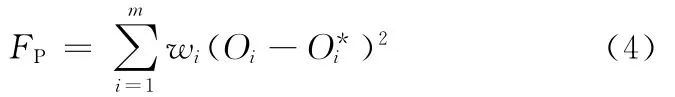
式中，Oi、O＊i分别为模型响应输出与对象响应输出中第i个极值的采样序号；wi为相应权重，出现越早的极值权重越大。

考虑到LSM辨识的系统模型具有较好的相位精度，而GA辨识的系统模型具有较好的幅值精度，本文提出一种基于多目标优化的新型模型辨识方法：以最小二乘法的辨识模型为进化导师，在多目标遗传算法的原始种群中选择Pareto优于进化导师的个体为精英，保证精英具有较均衡的幅值精度和相位精度，利用无损有限精度法保持精英种群的多样性，再通过多指标聚合函数计算精英的适应度，完成精英个体的邻域变异、单目标个体的全局变异以及两者的启发式交叉。算法实现流程如图5所示。

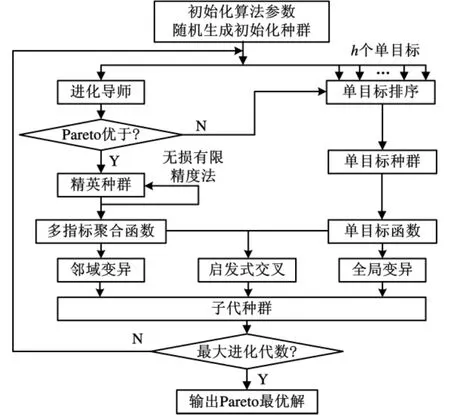
图5 多目标遗传算法实现流程

3.1 进化导师

Pareto优化定义 对多目标优化问题中的两个决策向量x和y（xj，yj∈ ［a，b］，a、b分别为决策变量定义域的下上限），如果两者的多目标函数fi（y）≤fi（x）（i＝1，2，…，M）中至少有一个严格不等式成立，则称x是Pareto优于y，记为x≻y。

可见，以LSM的辨识模型XLSM为进化导师，在原始种群中选择Pareto优于XLSM的个体为精英，则可保证多目标遗传算法的精英个体具有不劣于XLSM的相位精度，根据多指标聚合函数搜索的Pareto最优解必然具有较均衡的优化性能。

3.2 无损有限精度法

多样性保持机制是多目标优化方法的一个研究重点，MOGA［6］中的惩罚距离小于规定值的两个个体，NSGA－Ⅱ［8］采用个体的拥挤距离作为虚拟适应度，这些方法都需要较大的计算量。祁荣宾等［10］提出一种不增加算法计算量的有限精度法，人为地降低目标函数的求解精度，淘汰函数值相同的个体。该方法以损失求解精度为代价，且计算对象为目标函数，并不能从模型参数角度反映个体的差异性，因此，本文从模型参数角度，提出一种不损失求解精度的无损有限精度法，实现流程如下：

3.3 多指标聚合函数

该函数继承了拥挤距离［8］和向量模的思想，但并非简单地将目标空间中的个体视为m维空间的向量，而是根据每个目标函数将所有个体升序排序，函数值经过归一化处理作为m维向量中的一个分量，再计算个体的向量模。在第k（1≤k≤m）组函数序列中，对排序等级为i的个体，其第k个目标函数值的归一增量距离为

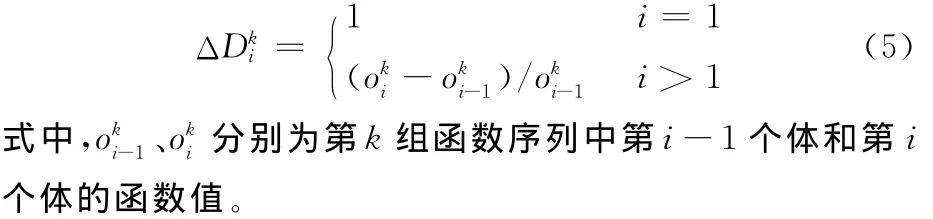
在每组函数序列中，先根据式（5）计算个体的m个归一增量距离，再采用向量模的方法计算多指标聚合函数：

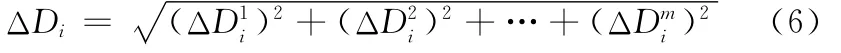
3.4 模型辨识试验

下面采用这种基于多目标优化的新型模型辨识方法进行试验，以误差准则式（2）和式（4）为优化目标，以LSM的辨识模型XLSM为进化导师，以无损有限精度法保持种群多样性，以多指标聚合函数进行Pareto寻优。经过5次随机试验，辨识的模型参数如表3所示。表3中直接列出两种误差准则的函数值，5次辨识结果非常接近，目标向量的平均值为［28.4794 47］，均方差为［0.1931 0］，可以看出，只有幅值误差存在细微差别，相位误差完全相同，各个参数也比较接近，算法的收敛能力有很大提高。

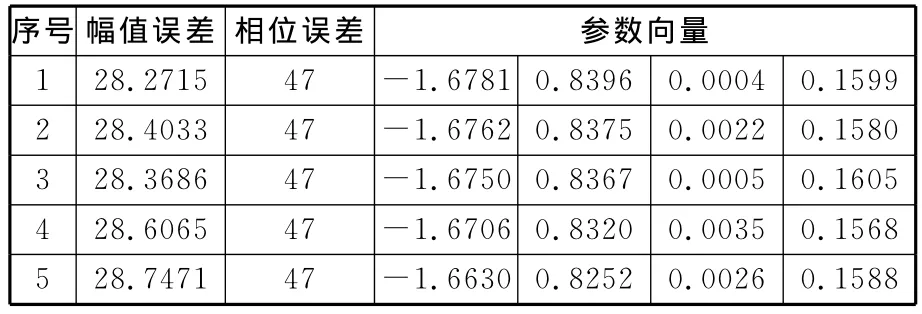
表3 新方法辨识的模型参数

在表3中，第1次辨识模型的幅值误差最小，第5次辨识模型的幅值误差最大，绘制前者的阶跃响应曲线，如图6点划线所示。在前三个波峰位置，该模型响应曲线无论在幅值方面还是在相位方面都比较逼近对象响应曲线，明显优于SCGA和SAGA的辨识结果。新方法的辨识结果将为AGV伺服控制系统设计提供更为精确的系统模型。

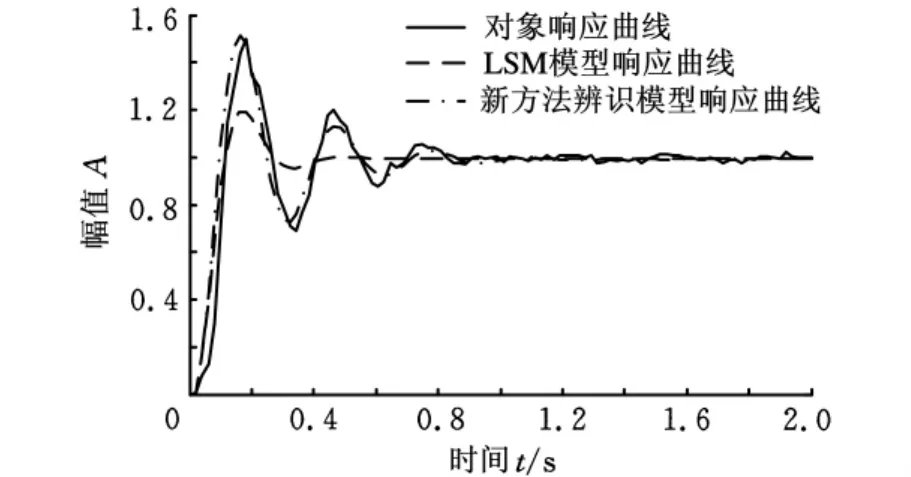
图6 新方法辨识的模型响应曲线

4 结束语

针对最小二乘法和单目标遗传算法在模型辨识时遇到的问题，本文同时考虑了幅值精度和相位精度两个优化目标。以最小二乘法的辨识模型为进化导师，发挥其在相位精度优化方面的优势；以无损有限精度法为多样性保持机制，避免了种群容易发生的早熟现象；以多指标聚合函数为精英个体的适应度函数，提高了对Pareto最优解的搜索能力。在AGV驱动系统的模型辨识试验中，该方法辨识的系统模型与实际对象较为吻合，这将为设计高性能的AGV伺服控制器打下良好的基础。

［1］ 宋立博，李劲松，费燕琼.四轮差动驱动型AGV嵌入式运动控制器设计与研究［J］.中国机械工程，2008，19（24）：2903－2907.

［2］ 陈无畏，李碧春，孙海涛，等.基于视觉导航的AGV模糊－最优控制研究［J］.中国机械工程，2006，17（24）：2546－2550.

［3］ 武星，楼佩煌，杨雷.基于视野状态分析的机器人路径跟踪智能预测控制［J］.机器人，2009，31（4）：357－364.

［4］ Liu Depeng.Genetic Algorithms based Parameter Identification for Nonlinear Mechanical Servo Systems［C］／／IEEE Int.Conf.on Industrial Electronics and Applications.NJ，USA：IEEE，2006：1－5.

［5］ Shin G W，Song Y J，Lee T B，et al.Genetic Algorithm for Identification of Time Delay Systems from Step Responses［J］.Int.J.of Control，Automation and Systems，2007，5（1）：79－85.

［6］ Fonseca C M，Fleming P J.Multiobjective Optimization and Multiple Constraint Handling with Evolutionary Algorithms–Part I：a Unified Formulation［J］.IEEE Trans.on System，Man and Cybernetics–Part A：Systems and Humans，1998，28（1）：26－37.

［7］ Leung Yiuwing.Multiobjective Programming Using Uniform Design and Genetic Algorithm［J］.IEEE Trans.on System，Man and Cybernetics Part C：Application and Reviews，2000，30（3）：293－304.

［8］ Deb K，Pratap A，Agarwal S，et al.A Fast and Elitist Multiobjective Genetic Algorithm：NSGAII［J］.IEEE Trans.on Evolutionary Computation，2002，6（2）：182－197.

［9］ 张世华，雎刚.一种实数编码的自适应遗传算法及其在热工过程辨识中的应用研究［J］.中国电机工程学报，2004，24（2）：210－214.

［10］ 祁荣宾，钱锋，杜文莉，等.基于精英选择和个体迁移的多目标遗传算法［J］.控制与决策，2007，22（2）：164－168.

Model Identification Based on Multi－objective Optimization for AGV Driving Systems

Wu Xing Lou Peihuang Tang Dunbing
Nanjing University of Aeronautics and Astronautics，Nanjing，210016

A novel model identification approach based on least square method and multi－objective genetic algorithm was presented for the driving system of AGV.The model identified by least square method was adopted by multi－objective genetic algorithm as an evolution tutor who selected these individuals having a balance among a set of objective performances as elitists.Lossless finite precision method was used to keep the population diversity，and a multi－objective combined function was designed for a quick search for Pareto optimal solutions.The model identification experiments of AGV driving system demonstrate that the response curve of the model identified by the novel approach is much consistent with the object response curve both in amplitude and phase，which will provide a precise system model for AGV servo control system design.

automated guided vehicle（AGV）；model identification；genetic algorithm；multi－objective optimization

TP301

1004—132X（2011）10—1164—05

2010—04—28

南京航空航天大学基本科研业务费专项科研项目（NJ2010025）；南京航空航天大学引进人才科研启动基金资助项目（S1026－053）

（编辑 袁兴玲）

武 星，男，1982年生。南京航空航天大学机电学院讲师。主要研究方向为移动机器人、运动控制和嵌入式控制等。楼佩煌，男，1962年生。南京航空航天大学机电学院教授、博士研究生导师。唐敦兵，男，1972年生。南京航空航天大学机电学院教授、博士研究生导师。