基于时栅传感器的传动误差动态测试系统研制

彭东林 郑 永 陈自然 高忠华 郑方燕

1.合肥工业大学，合肥，230009

2.重庆理工大学机械检测技术与装备教育部工程研究中心，重庆，400054

基于时栅传感器的传动误差动态测试系统研制

彭东林1，2郑 永1陈自然1高忠华2郑方燕2

1.合肥工业大学，合肥，230009

2.重庆理工大学机械检测技术与装备教育部工程研究中心，重庆，400054

传统的传动误差动态测试系统采用光栅作为角度传感器，而高精度光栅价格昂贵且进口受限，针对该情况，采用拥有自主知识产权的时栅位移传感器，通过时间序列模型将时栅由绝对式信号转化为增量式脉冲信号。结合成熟的全微机化齿轮机床精度检测分析系统（FMT系统）对滚齿机进行了传动误差动态测量，准确度达到0.137%，实现了预期目标。

时栅；传动误差；动态测量；时间序列

0 引言

对于要求高质量传动的场合来说，实现机械传动链的传动误差动态测量有重要的意义。通过对整条传动链传动误差的精密测量，可以得到准确的传动关系。高精度的零件不一定带来高精度的传动，传动还和零件之间的配合等因素有着密切的关系。只有通过对传动链传动误差的动态测量，并对其作出客观正确的评价，准确分析出产生这些误差的原因，才能为零件的加工、选配和安装提供指导性的依据，达到事半功倍的效果。传动误差的动态测量一般是以光栅作为角度传感器，光栅的精度直接影响最终传动误差测试的结果。现在国产的光栅精度不高，高精度的光栅主要通过进口，市场上常见的品牌有德国海德汉、英国雷尼绍等。一般能够从市场上购买到的进口光栅最高精度为±1″，更高精度指标光栅的购买受到限制。角度传感器是数控设备的“心脏”，长期受制于人将会制约我国机械行业的发展。时栅位移传感器是一项原创性的发明［1－2］，与传统栅式传感器相比，在结构、制造工艺、抗干扰性和成本等方面有明显的优势。

1 时栅及传动误差动态测试原理

通过建立带时间考查点的相对运动双坐标系，把一个坐标系上的绝对空间位移的测量转换成另一个坐标系上的相对时间差测量［1］，可以实现位移测量中测量基准的时空转换，使时钟脉冲具有空间意义。于是从理论上说，采用此方法可以获得一种新的位移传感器，它把传统栅式传感器中对空间分度的要求转换成对时间分度的要求，这种传感器的分辨力和精度在很大程度上取决于时钟脉冲的频率和精度，称之为时栅位移传感器。

根据传动误差（TE）的定义，传动链误差反映的是传动链两端运动位移的相对差异部分。设传动比为I（I≥1），高速端理论角位移为Φ1，实际角位移为φ1，低速端理论角位移为Φ2，实际角位移为φ2，则TE的推导及演变过程［2］如图1所示。

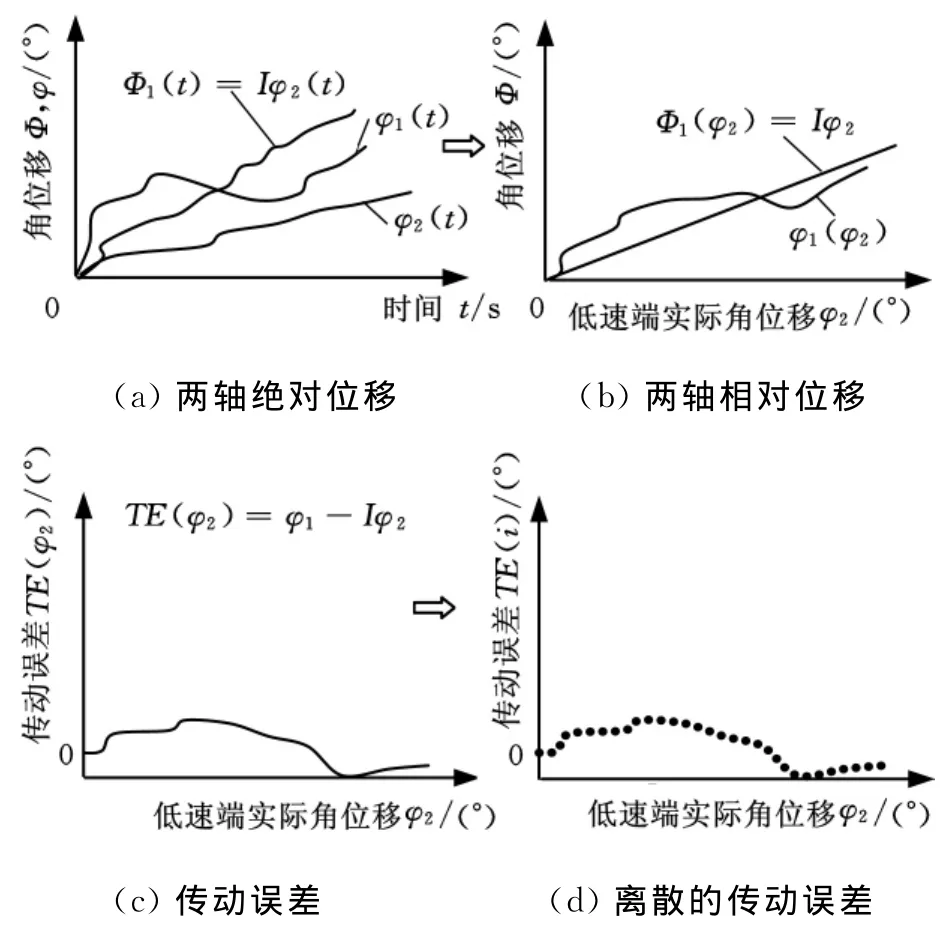
图1 传动误差TE推导图

图1a所示是高低速端传感器随时间变化的实际角度曲线，高速端的理论角度Φ1是根据传动比I和低速端角度φ2计算得到的。图1b是将横坐标变为了低速端实际角度，将图1a中的曲线φ1（t）和Φ1（t）进行了变换，变为以φ2为自变量的角度曲线。图1c是在图1b基础上计算的传动误差。图1d是将图1c中连续曲线离散化，这样做的目的是为了能够实现离散采样。

传动误差测量［3］所采用的同步位移比较法是以传动装置的某一端（即参考轴）的位置为基准，去比较另一端的位置，这是一种等空间间隔采样。而时栅可以理解为一种定时扫描的绝对位置传感器，因此通过它的采样值得到的是按时间均分给出的时域误差曲线，横坐标是时间量t，即等时间间隔采样。对此矛盾，本研究首先考虑采用“时域采集、空域分析”的思路，方案如下：第一步，同时对高低速端进行采样，按时间等分得到采样信号（图2a）。因为被测运动是一个连续的运动过程，客观上存在一条连续的位置随时间变化的曲线，因此，第二步按某种函数规律（如最简单的线性函数）分别拟合出一条连续曲线（图2b）。第三步，将此连续曲线φ2（t）重新按空间等分，分割为新的φ2的离散数组（曲线）（图2c）。据此曲线再一一对应找出新的φ1的离散数组（曲线），这样，就可以得到与图1d具有同样意义的传动误差数组及曲线，如图2d所示。

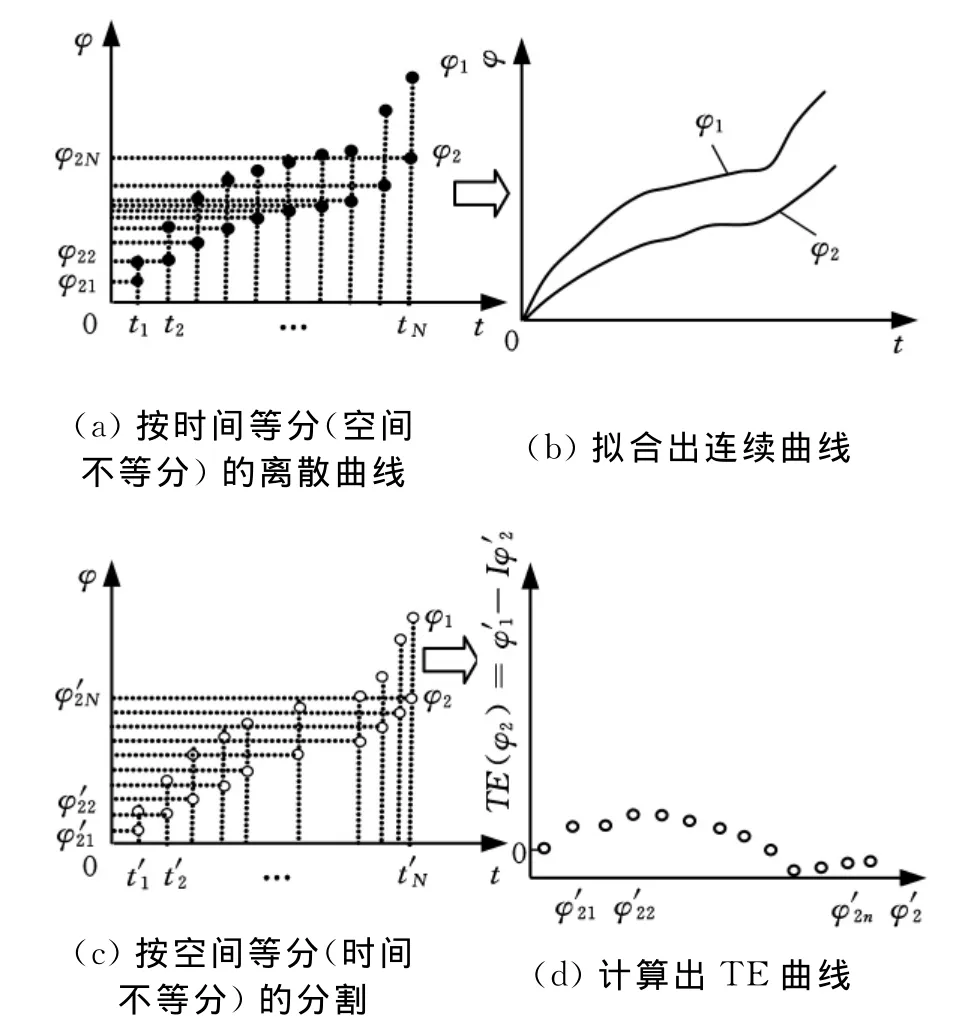
图2 时栅测量TE推导图

这种方法的优点在于，两路时栅加上同步触发电路就可以测量TE曲线，原理清晰简单。而不足之处在于：①由于是等时间采样测量，而运动是不匀速的，于是每次测量的起点都是不同的，不能保证任意两周的采样曲线采样各点在物理位置上是重合的，因此不便从多次连续测量曲线的重合性上来判断整个测试系统的示值稳定性；②传动误差曲线只能在测试完毕，经过拟合等运算后才能显示，不能实时显示；③人们长期使用增量式光栅或磁栅所积累的宝贵实践经验［4-5］不利于被再利用。

为了解决上面的问题，本研究提出从传感器的层面着手将时栅绝对角度信号转化为增量式脉冲，用增量式脉冲来实现TE测量的方案。这样就可以沿用成熟的全微机化齿轮机床精度检测分析系统（FMT系统）［4-5］进行测量。

2 时栅信号由绝对式向增量式转化

时栅每隔时间T采样一次得到绝对角度值，前n个时刻（从时刻tj－（n－1）至tj）的角度测量值为θj－（n－1），θj－（n－2），…，θj，可视为一个时间序列。可以建立时间序列模型来对它的未来取值进行预测，从而产生增量式脉冲［6-7］。

预测测量原理如图3所示。首先利用时栅前n个时刻的绝对角度测量值θj－（n－1），θj－（n－2），…，θj，在当前时刻tj预测出下一个测量周期T（从时刻tj至tj＋1）内时栅的角位移值 Δ＾θj＋1，并在下一个测量周期T内发出代表角位移预测值Δθj的增量式脉冲信号。采用这种预测方法就可以把绝对式离散角度测量值转化为增量式连续脉冲信号。时栅第j个测量周期（从时刻tj－1至tj）内时栅角位移为

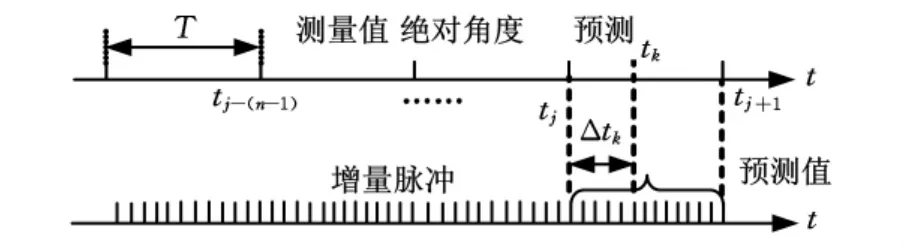
图3 预测测量原理

通过对时栅现在和过去n个采样周期T的角位移值θj－（n－1），θj－（n－2），…，θj进行建模，利用时间序列理论，得到下一个时栅测量周期（从时刻tj至tj＋1）内的角位移预测值：

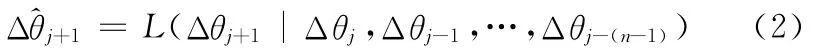
则在下一个时栅测量周期（从时刻tj至tj＋1）内采用脉宽调制（pulse－width modulation，PWM）方式输出的脉冲个数为

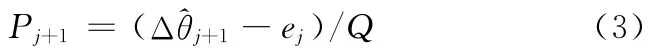
式中，ej为上一个周期（从时刻ti－1至tj）内的预测误差；Q为脉冲当量。

式（3）中加入了对上一个周期预测误差的修正，预测误差是前一个周期（tj－1时刻）的预测值Δθj与本次（tj时刻）时栅测量得到的角度增量的差值。通过这样的处理，预测产生的误差会在下一个周期进行补偿，这样就可以保证高精度的测量。利用p阶自回归模型AR（p）对时间序列｛Xt｝进行建模，具体的表达式为

其中，｛εt｝是白噪声WN（0，σ2），实数φi是AR（p）模型的自回归系数，且φi≠0。对于AR（p）模型，利用p个数据Xn，Xn－1，…，Xn－p＋1对Xn＋1进行递推预测，最佳线性预测表达式为

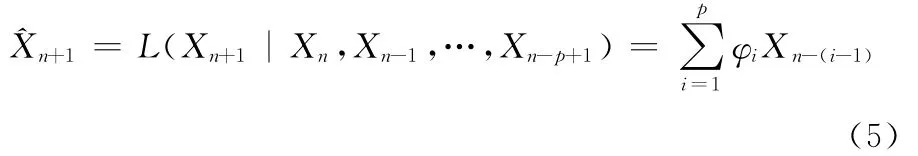
对观测数据X1，X2，…，XN进行零均值化的预处理：

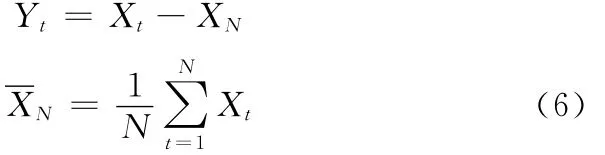
为数据｛Yt｝构建一个AR（p）模型，再根据观测样本X1，X2，…，XN可以构造出样本自协方差函数的估计：

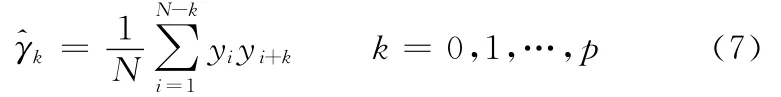
这样，经过处理后，可以实现时栅信号由绝对式向增量式的转化，时栅信号最终转变为增量式脉冲信号。

3 实验研究

为验证时栅转化为增量式脉冲信号的效果，专门设计了一个实验台。实验台主要由数控转台、海德汉圆光栅、时栅传感器组成。数控转台的作用是提供一个匀速回转轴，同时带动圆光栅和时栅同步转动。为了保证回转速度稳定，数控转台中采用西门子数控系统控制伺服电机。

圆光栅用来对时栅转化的增量式脉冲信号进行标定，圆光栅采用36 000线、精度为±1″的ROD880。为了提高光栅信号的分辨力，将其输出的正弦信号先经过海德汉IBV660B细分盒进行100倍细分，然后将细分后的信号通过数字电路进行4倍细分，细分后的脉冲信号最终分辨力为0.09″。ROD880经过细分后的脉冲信号和时栅的增量式脉冲信号一同接入计数电路，两路计数器分别对两路脉冲进行计数，并可以同步锁存两路计数器从而实现同步位移比较。实验台如图4所示。

图4 实验装置图

待转化的时栅传感器精度为±1.2″时，整个过程在相对匀速的条件下进行，最后的预测误差在［－2″，2″］以内。

4 时栅传感器应用于机床传动误差测量

应用时栅传感器测量机床传动误差，测试现场如图5所示。

图5 现场测试图

被测机床为重庆机床厂生产的滚齿机Y3180H，机床传动链如图6所示。

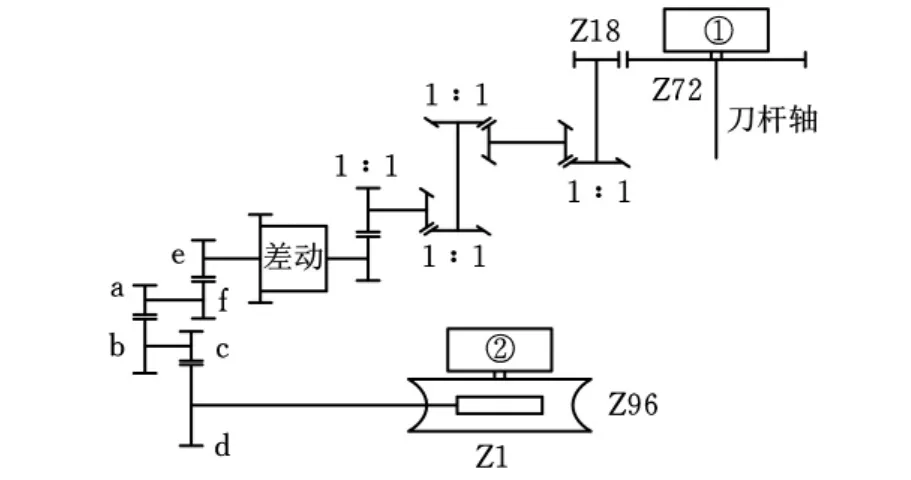
图6 机床传动链

图6中①为高速端时栅传感器，②为低速端时栅传感器。刀杆和转台按传动比100选择挂轮a、b、c、d。实际测试传动误差曲线如图7a所示，图7b为其频谱图。

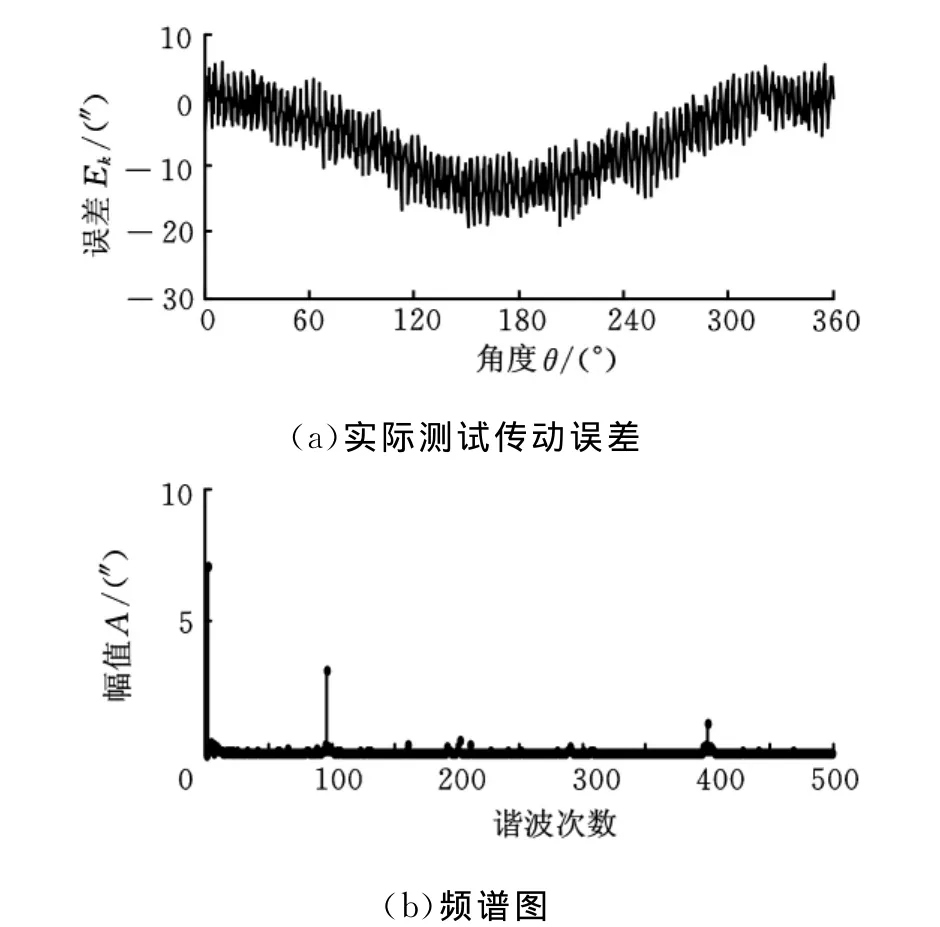
图7 传动误差测试结果

从图7可以看出排在前几位的谐波次数为1、96和400。由图6可知，1次谐波误差是由工作台的蜗轮引入的；96次是由机床的工作台的蜗杆引入的；锥齿轮转速是刀杆的4倍，而机床的传动比为100，因此400次谐波是由锥齿轮引入的。这就证明本机床的三个主要误差环节是工作台蜗轮、工作台蜗杆和锥齿轮，这也符合人们的预测。根据机床传动链误差传递卡拉希尼柯夫误差理论［3］可知，传动链中每个传动件传动误差的主要部分均为其转角的正弦（或余弦）函数，传动链各传动件传动误差幅值按照传动比进行传递，并且在末端件上以矢量形式叠加。因此既可以根据机床传动误差测试曲线对机床的整个精度情况进行准确掌握，也可以根据频谱分析结果对相应零部件产生的原始误差进行分析，进而对机床进行维修或提高精度。

采用机械移相法对测试系统准确度进行了校验。机械移相法是一种利用人为制造已知误差，对仪器进行自我检验的方法，其检定过程如图8所示。

实验过程如下：在高速端传感器的拨杆某个位置放置一个百分表，百分表平面与传感器平面平行，与传感器中心距为r，记下百分表读数c1。实验曲线如图9所示，先让机床工作台正常旋转一周，得出一条正常测试曲线。第二转进行自检，当第二转开始一段时间后插入量块，记下百分表的读数c2，过一段时间后取出量块，百分表读数恢复为c1。与量块插入相对应，实时测试曲线将在原有与第一转重合的轨迹上上移一段距离（根据传感器的转向决定上移或下移，这里为上移）；再测一段时间后，取出量块，测试曲线又将下移一段距离，恢复到与第一转重合的状态。

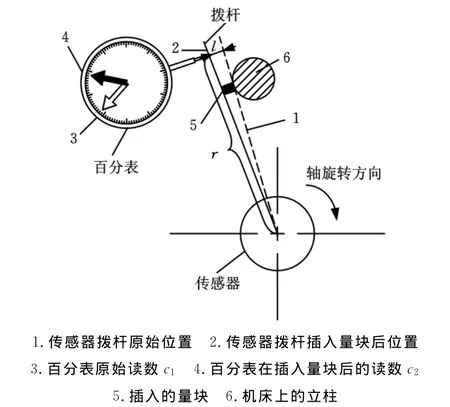
图8 机械移相法示意图

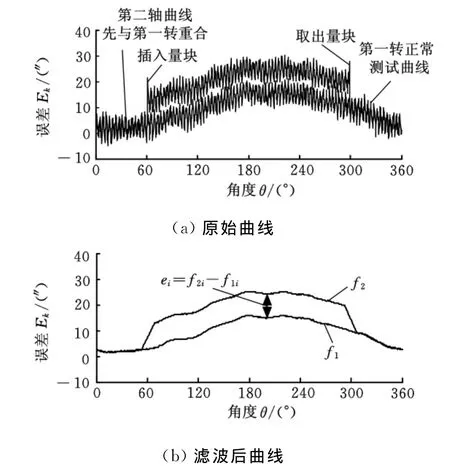
图9 机械移相法测试图

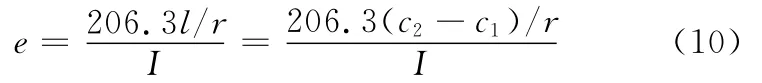
通过式（10）将l折换成为低速端的角度值e，e值就是人为制造误差的角度真值。其中I是机床当时工作台与刀杆轴传动比。

将第一转和第二转曲线插入量块和取出量块区间的数据点依次地分别抽取n个点fi，一一对应相减，以此作为仪器反映出的人为制造误差值的测得值：ei＝f2i－f1i，最后取平均就得到仪器准确度E：

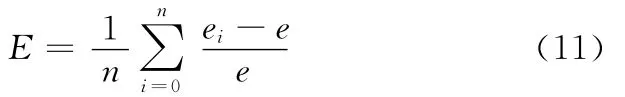
这时百分表读数差值即c2－c1就是人为制造误差的线性真值l，已知百分表与拨杆接触点到传感器中心的距离r，则有

以图8、图9为例，r＝145mm，同时记下百分表读数c1＝0，c2＝0.650mm，即l＝650μm，传动比I＝100，理论计算的人为制造误差角度真值e＝650×206.3／（145×100）≈9.2″；从工作转角80°到280°这一段可逐点比较f2i和f1i的数据差ei，均与e十分接近。代入式（11）最后得出仪器的准确度为：E＝0.137%。

5 结论

（1）时栅信号通过时间序列预测法转换成增量信号的方法切实可行，传感器转换后对机床测试的准确度达到0.137%。

（2）通过时栅传感器的增量式脉冲工作方式测量传动误差，可以准确地反映真实的机床误差状况，测试曲线的频谱分析可以与实际的传动链相对应。

（3）按照经典的卡拉希尼柯夫误差理论［3］，高频振动引起的误差将大部分被传动链中的弹性环节（如滚齿机中加长的蜗杆）所吸收，并且高频误差只影响产品的表面粗糙度，不属于传动误差的研究范畴，在本文中未作描述。

［1］ 彭东林，刘成康，谭为民.时空坐标转换理论与时栅位移传感器研究［J］.仪器仪表学报，2000，21（4）：338－342.

［2］ 彭东林.时栅位移传感器与新型机床动态检测系统［M］.北京：科学出版社，2010.

［3］ 和子康.机床传动精度测量和提高［M］.北京：中国计量出版社，1987.

［4］ 彭东林，谭为民，刘小康.空域分析法及其在传动误差测量中的应用［J］.工具技术，2003（4）：34－36.

［5］ 彭东林，张光辉，郭松涛，等.传动误差检测系统FMT［J］.制造技术与机床，1996（5）：20－22.

［6］ Frantisek S.Predictions in Time Series Using Regression Models［M］.New York：Spinger－Verlag，2002.

［7］ 何书元.应用时间序列分析［M］.北京：北京大学出版社，2007.

The Development of Transmission Error Dynamic Measurement System Based on Time Grating Displacement Sensors

Peng Donglin1，2Zheng Yong1Chen Ziran1Gao Zhonghua2Zheng Fangyan2
1.Hefei University of Technology，Hefei，230009
2.Engineering Research Center of Mechanical Testing Technology and Equipment，Ministry of Education，Chongqing University of Technology，Chongqing，400054

Optical gratings are applied to traditional transmission error dynamic measurement system as angle detecting sensors，but high－precision optical gratings are expensive and imported restrictedly.In view of this situation，a time grating，the novel displacement sensor of proprietary intellectual property rights，is invented.Absolute displacement signal of time grating is converted into incremental pulse signal with time series models.and the experiment results prove that accuracy of measurement can achieve 0.137%by using sophisticated FMT test transmission error of gear－hobbing machine，so the desired schematic design has been obtained.

time grating；transmission error；dynamic measurement；time series

TH7

1004—132X（2011）10—1138—05

2010—10—20

国家自然科学基金资助项目（50805150，50975304）

（编辑 袁兴玲）

彭东林，男，1952年生。合肥工业大学特聘教授，重庆理工大学电子信息与自动化学院教授。主要研究方向为精密测试技术及仪器。郑 永，男，1983年生。合肥工业大学仪器科学与光电工程学院博士研究生。陈自然，男，1980年生。合肥工业大学仪器科学与光电工程学院博士研究生。高忠华，男，1972年生。重庆理工大学机械检测技术与装备教育部工程研究中心讲师。郑方燕，女，1972年生。重庆理工大学机械检测技术与装备教育部工程研究中心讲师。