基于像底点的机载POS视准轴误差检校
2011-01-31付建红赵双明
付建红,赵双明
武汉大学遥感信息工程学院,湖北武汉430079
1 引 言
在航空摄影测量中,像片外方位元素的求解是关键问题之一,传统方法是先将测区中的所有影像经连接点构成区域网,然后通过空中三角测量方法,依靠大量地面控制点进行整体求解。近几年,集差分GPS和惯性导航系统(inertial navigation system,INS)于一体的机载POS系统为像片外方位元素的确定提供了一种新的方法,并在航空遥感中得到了广泛应用[1-4]。如文献[2]研究了利用POS辅助光束法区域网平差,可减少野外像控点的联测工作。然而,由于安装的原因, IMU的坐标轴系与航摄仪的坐标轴系并不能够保持严格平行,两个坐标轴系之间存在一个小角度的偏差,通常称之为视准轴误差或偏心角[5-6],从而导致 POS系统提供的像片外方位角元素不能直接用于对地目标定位,需要采用合适的检校方法进行误差补偿。
当代摄影测量理论的重要发展之一是将灭点理论应用于摄影测量,主要用于相机的标定和建筑物三维重建[7-9]。文献[7]利用多像灭点进行近景摄影测量相机的标定,通过灭点直接建立待标定参数与观测值之间的函数模型,从而对相机内外参数联合平差,提高了相机的标定精度。文献[8]将灭点理论和平面控制场相结合用于计算机视觉中的相机标定。文献[10]利用灭点确定相机内方位元素与外方位角元素。对于航空摄影而言,空间一组铅垂线在影像上的灭点称为“像底点”,同时也是通过投影中心(摄站点)的铅垂线与像平面的交点,其像平面坐标和影像的摄站坐标(外方位线元素)无关,而只和影像的外方位角元素有关[11]。文献[11—12]将像底点约束作为一种新型控制条件引入城市大比例尺空中三角测量,并取得了较好的试验结果。本文基于以上研究思想,提出一种利用像底点检校机载POS系统视准轴误差的新方法,从理论上建立像底点与POS系统视准轴误差之间严格的数学关系,然后在此基础上推导了求解视准轴误差的误差方程式,最后用试验验证了方法的可行性。
2 基于像底点的视准轴误差检校
2.1 视准轴误差
带POS系统的航空摄影在设备安装时,必须将IMU与航摄仪固连在一起,并要求IMU本体坐标系与航摄仪本体坐标系的相应坐标轴保持相互平行,如图1所示。只有这样,IMU所测定的姿态角才等同于航摄仪的姿态角。但是,在设备实际安装时,要保证两个坐标系的坐标轴严格相互平行是不可能的,相应坐标轴之间必然会存在一个小的夹角。为了实现坐标轴的相互平行,需将IMU本体坐标系进行三次旋转。假定旋转顺序为先绕 xb轴旋转ex,然后绕旋转后的 yb轴旋转ey,最后绕两次旋转后的zb轴旋转ez,则ex、ey、ez一般称之为视准轴误差或偏心角误差[5-6],如图2所示。其所构成的旋转矩阵R(ex,ey,ez)可表示为

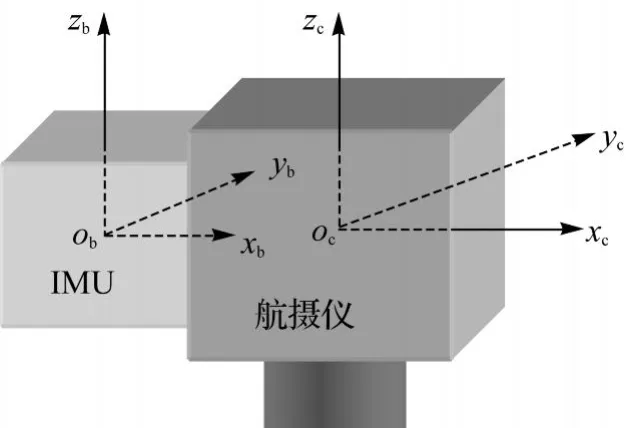
图1 IMU与航摄仪的几何关系Fig.1 Geometricrelationship between IMU and camera

图2 视准轴误差Fig.2 Boresight misalignment
假定航空摄影时像片的实际外方位角元素为φ、ω、κ,其所构成的旋转矩阵为R,而由IMU直接所测定的像片外方位角元素为φ0、ω0、κ0,其所构成的旋转矩阵为 R0。顾及视准轴误差所构成的旋转矩阵,三者之间的相互关系可表示为[3,6]

2.2 基于像底点的视准轴误差检校模型
中心投影方式下,物方空间一组铅垂线在像平面上的投影会交于一个“灭点”。在航空摄影测量中,该点又称为“像底点”,也可以认为是通过投影中心(摄站点)的铅垂线与像平面的交点。假设航摄仪的主距为 f,摄影时像片的外方位角元素构成的旋转矩阵则由共线条件方程可以求得像底点的坐标为[13]

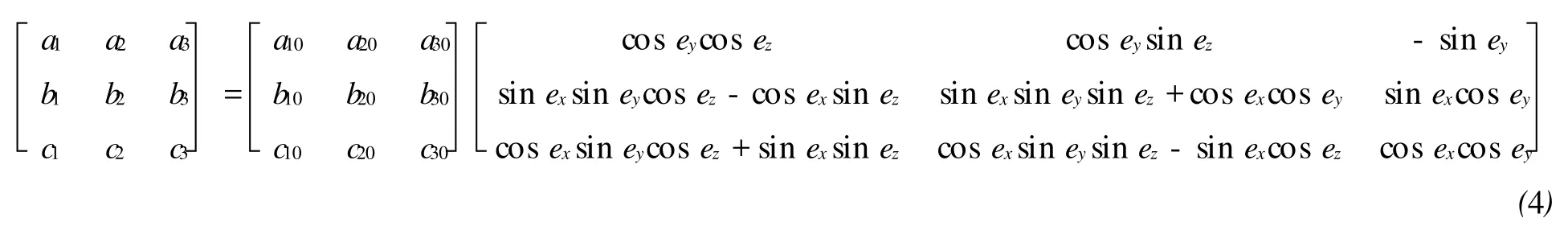
根据式(3)、式(4)可得像底点与视准轴误差之间严格的数学关系为

式(5)即为基于像底点的视准轴误差检校模型。分析式(5)可知,c10、c20、c30分别为IMU直接测定的像片外方位角元素所构成的旋转矩阵中的三个元素。由于IMU最终提供的姿态角一般经过了DGPS/IMU数据联合后处理,在数据后处理中已经经过了严格的误差模型改正,因此,c10、c20、c30可认为是已知值;ex、ey、ez为需要求解的POS系统的视准轴误差,对于同一航摄区里的所有像片而言,其可认为是一个常数值。所以,只要得到该试验区内两张或以上像片上的像底点坐标,利用式(5)即可求解出 POS系统的视准轴误差。
2.3 像底点观测的误差方程式
式(5)是一个非线性方程,在求解未知数时需要先对其进行线性化。可设定各未知参数的初值为0,按泰勒级数展开取至一次项可得

式中,vxn、vyn和Δex、Δey、Δez分别为像底点坐标xn、yn和视准轴误差ex、ey、ez的改正数;xn0、yn0为给定初始值ex=0、ey=0、ez=0的情况下按照式(5)所计算出来的像底点坐标;xn,yn为像片上铅垂线交会得到的像底点坐标,可认为是观测值。由于ex、ey、ez均为小角度(<3°)[14],在进行误差方程式系数推导时可采用简化公式(cose=1、sine=e),并略去小值的高次项,则式(5)可写为

如果令
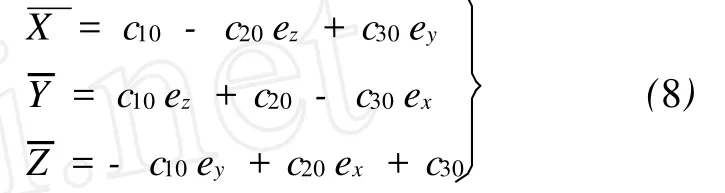
则式(6)中误差方程式的各个系数为

在实际解算时,首先利用两张或以上像片上铅垂线的投影交会确定各自的像底点坐标,并根据式(6)建立误差方程式,再采用最小二乘平差方法便可以迭代求解出机载POS系统的视准轴误差ex、ey、ez。
2.4 视准轴误差检校流程
根据以上理论分析,利用像底点进行视准轴误差检校的详细流程如图3所示。
3 试验设计及检校结果
3.1 试验数据简介
为了验证本文提出的利用像底点检校 POS系统视准轴误差方法的正确性及其求解精度,选择某地区带POS系统飞行的大比例尺航空影像进行试验验证。影像为采用主距153.84 mm的Leica Rc-30航摄仪成像于 Kodak 2444胶片上所形成,像幅大小为23 cm×23 cm。加装的POS系统为加拿大Applanix公司的POS AV 510系统。航空摄影时,在试验区2个基准站上各安置了一台Astech双频GPS接收机,数据采样间隔设置为2 s。试验区覆盖有正常重叠度飞行的9条航线,共255张像片。

图3 利用像底点检校视准轴误差流程Fig 3 Flowchart for boresight misalignment calibration by using nadir point
航空摄影完成以后,将航摄负片扫描成21μm的数字化影像,并对POS数据用其自带的后处理软件 POSPac[15]进行处理,得到每张像片的6个初始外方位元素。为了得到POS系统的视准轴误差,选择试验区西北角3条航线×7张像片的一个区域作为检校场用于求解系统误差[16]。首先对检校场影像进行自动量测和转点,然后将影像连接点导入POS系统自带的检校软件POSCal[15]解算视准轴误差,以用于分析本文检校方法的结果及精度。
3.2 理论像底点检校结果
从以上分析可知,在利用像底点检校POS系统的视准轴误差时,首先要利用物方铅垂线在影像上的投影交会确定像底点坐标,而其交会精度会直接影响视准轴误差的检校结果。为了避免像底点交会误差对后续视准轴误差检校结果的影响,笔者首先从试验区中选定3张像片的POS外方位元素,然后人为给定一组视准轴误差(如表1所示)对其进行改正,并用改正后的外方位元素按照式(3)计算出3张像片上的像底点坐标。用此组不含任何误差的理论像底点坐标求解POS视准轴误差,结果列于表1。

表1 理论像底点检校结果Tab.1 Calibration results by using photo nadir points in theory arc min
从表1中可以看出,理论像底点检校出的视准轴误差与给定值非常接近,ex、ey的差值绝对值均为0.018 arc sec(0.000 3 arc min×60);ez相差0.18 arc sec(0.003 arc min×60)。这一差值可以认为是由于计算过程中的舍入误差所引起。由此可见,本文所提出的基于像底点检校POS系统视准轴误差的方法和建立的数学模型是正确的。比较三个差值还可以看出,ez的差值较ex和ey明显较大,其主要原因是由于航摄像片一般为竖直摄影,要求像片在获取时刻航摄仪应尽量水平,而κ角为像片绕主光轴的旋角,在理想情况下(像片严格水平),像底点κ与角的大小无关。所以像底点可较好地约束像片外方位角元素中的φ、ω,而对κ角误差的敏感性稍差,导致检校出来的ez精度较低,这与文献[12]中的研究结果也是一致的。有关像底点与外方位角元素误差之间的关系式可参考文献[11]。
3.3 像底点观测误差对检校结果的影响分析
在实际应用中,像底点是物方一组铅垂线在影像上的投影交会所得,所以实际交会得到的像底点必然包含一定的观测误差。为了分析像底点观测误差对POS系统视准轴误差检校结果的影响,笔者在理论像底点的基础上,对中间一张像片上的像底点加入了不同大小的观测误差,并重新进行视准轴误差的检校,其结果如表2所示。
分析表2中的试验结果,可以得出以下结论:①在9组试验中,ez的值变化不大,这说明像底点的观测误差主要影响ex、ey,而对 ez的影响不大,这与3.2节中的结论基本一致;②由前4组试验可以看出,像底点 x方向的误差主要影响ey,y方向上的误差主要影响ex,并且影响的大小与像底点观测误差的大小基本成正比;③对于本试验数据,当像底点观测误差分别为 1个像素(21μm)和1.5个像素(31μm)时,视准轴误差与理论值之差的绝对值(仅对 ex、ey)分别约为30 arc sec(0.5 arc min×60)和 42 arc sec(0.7 arc min×60)。由此可以看出,利用本文提出的基于像底点的POS系统视准轴误差检校方法只需将像底点的确定精度精确到像素级。根据文献[11]的研究结论可知,像底点的确定精度可以达到0.5~1.5个像素,所以本文方法在实际应用中是切实可行的,特别是对于目前广泛使用的高分辨率数码影像。
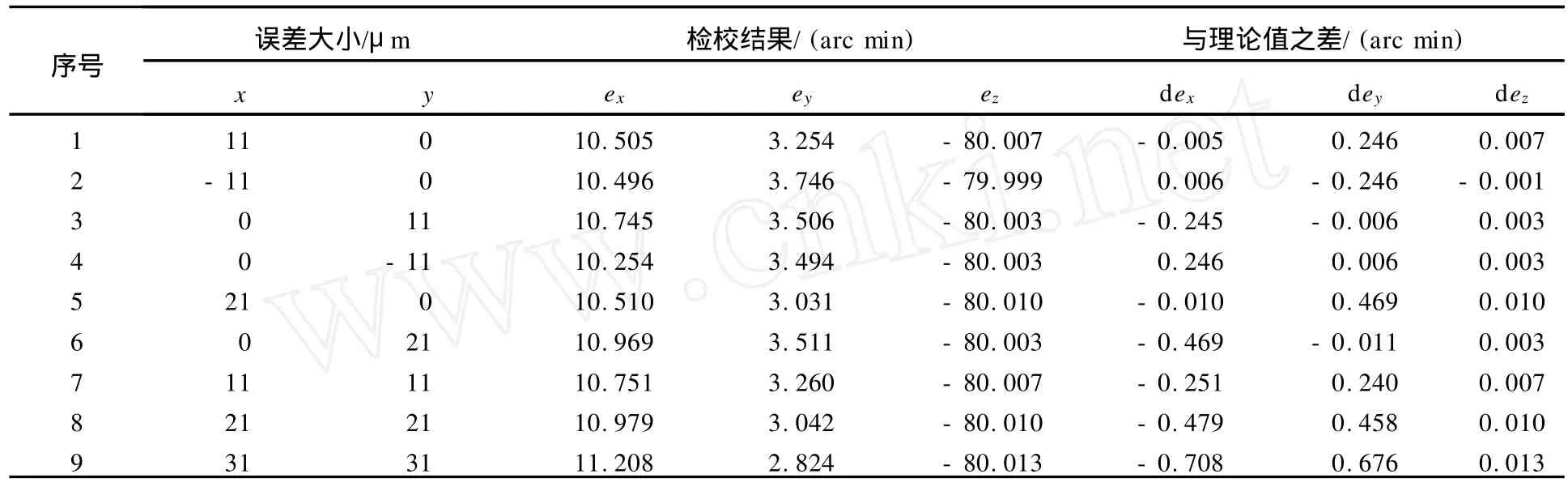
表2 像底点观测误差对检校结果的影响Tab.2 Influence on the calibration results caused by observation errors of photo nadir point
3.4 实际铅垂线交会像底点检校结果
为了分析利用像底点检校POS系统视准轴误差在实际应用中的效果,选择试验区中覆盖城区的3张像片进行铅垂线提取,并交会像底点坐标。铅垂线的提取方法和像底点的确定可参考文献[11],本文在此不做详细论述。提取的铅垂线分布及交会情况如图4所示。用实际交会出的像底点坐标进行POS系统视准轴误差检校,并和检校场检校结果进行比较,结果列于表3所示。

图4 铅垂线提取及交会示意图Fig.4 Diagrammatic sketch of vertical line extraction and nadir point intersection

表3 实际交会像底点与检校场检校结果比较Tab.3 Calibration results by using actual photo nadir point and comparison with the results from calibration field arc min
从表3可看出,实际交会出的像底点可以很好的检校出POS系统的视准轴误差。特别是对于角ex、ey,其与检校场检校结果的最大差值仅为5.46 arc sec(0.091 arc min×60);角ez的值与检校场检校结果相比较大,其原因如上文所述。像底点观测可较好的用于控制影像的姿态角φ和ω,而对κ角的约束性稍差。从试验结果可以看出,由于实际航空摄影时像片并非完全水平,所以视准轴误差ez中的绝大部分误差仍可较好的被检校出来,本次试验的检校值约达到97%(70.5/ 72.3),当然,在极端情况下(像片姿态角φ和ω接近于0),该方法尚不能正确求解 ez的值。此外,本文仅使用了3张像片上的像底点坐标,如果在检校时使用更多像片上的像底点坐标,有望进一步提高ez角的精度。
4 结束语
机载POS系统可直接测定航摄像片的外方位元素,避开传统的光束法区域网平差而实现直接对地目标定位,为基础地理信息的快速获取、更新和各种应急测绘提供保障。然而,POS系统视准轴误差的存在,大大降低了对地目标定位的精度。因此,目前在使用POS外方位元素时,必须利用检校场和地面控制点进行视准轴误差的检校以提高对地目标定位精度。本文基于灭点理论,提出利用像底点检校POS系统视准轴误差的新方法,该方法无须布设特定的检校场和地面控制点,仅需影像中有覆盖地面铅垂线信息的像片。笔者通过实例验证了本文方法的正确性和可行性,对带有POS系统的城区大比例尺航空摄影时的视准轴误差检校有一定实用意义。但该方法也存在一定缺陷,其缺点在于像底点对外方位角元素中的κ角误差的敏感性稍差,导致检校出的视准轴误差中ez角的精度较低,只能保证绝大部分误差被检校出来。
[1] MOSTAFA M M R,HUTTON J.Direct Positioning and Orientation System:How Do They Work?What is the Attainable Accuracy?[C/CD]∥Proceedings of American Society of Photogrammetry and Remote Sensing Annual Meeting.ST.Louis:ASPRS,2001.
[2] YUAN Xiuxiao.POS-supported Bundle Block Adjustment [J].Acta Geodaetica et Cartographica Sinica,2008,37 (3):342-348.(袁修孝.POS辅助光束法区域网平差[J].测绘学报,2008,37(3):342-348.)
[3] LI Xueyou.IMU/DGPS-supported Photogrammetry:Theory, Approaches and Practice[D]. Zhengzhou:Information Engineering University.(李学友.IMU/DGPS辅助航空摄影测量原理、方法与实践[D].郑州:解放军信息工程大学,2005.)
[4] YUAN Xiuxiao.A Novel Method of Systematic Error Compensation for a Position and Orientation System[J]. Progress in Natural Science,2008,18(8):925-934.(袁修孝.一种补偿POS定位测姿系统误差的新方法[J].自然科学进展,2008,18(8):925-934.)
[5] L I Xueyou,NI Zhongli.Research on Calibration Field Designing for IMU/DGPS-supported Photogrammetry[J]. Engineering of Surveying and Mapping,2005,14(4):14-18.(李学友,倪忠礼.IMU/DGPS辅助航空摄影测量中检校场布设方案研究[J].测绘工程,2005,14(4): 14-18.)
[6] YUAN Xiuxiao,YANG Fen,ZHAO Qing,et al.Boresight Misalignment Calibration of Integrated DGPS/IMU System[J].Geomatics and Information Science of Wuhan University,2006,31(12):1039-1043.(袁修孝,杨芬,赵青,等.机载POS系统视准轴误差检校[J].武汉大学学报:信息科学版,2006,31(12):1039-1043.)
[7] XIE Wenhan,ZHANG Zuxun.Camera Calibration Based on Vanishing Points of Multi-image[J].Acta Geodaetica et Cartographica Sinica,2004,33(4):335-340.(谢文寒,张祖勋.基于多像灭点的相机标定[J].测绘学报,2004,33 (4):335-340.)
[8] YANG Huachao,ZHANG Shubi,LIU Chao.Research into Camera Calibration Methods Based on the Vanishing Points Theory and Planar Control Fields[J].Journal of Image and Graphics,2010,15(8):1168-1174.(杨化超,张书毕,刘超.基于灭点理论和平面控制场的相机标定方法研究[J].中国图象图形学报,2010,15(8):1168-1174.)
[9] HEUVEL F A van den.Vanishing Point Detection for Architectural Photogrammetry[C].International Archives Photogrammetry and Remote Sensing:32(5).New York: Springer,1998.
[10] ZHANG Zuxun,ZHANG Jianqing.Generalized Point Photogrammetry and Its Application[J].Geomatics and Information Science of Wuhan University,2005,30(1): 1-5.(张祖勋,张剑清.广义点摄影测量及其应用[J].武汉大学学报:信息科学版,2005,30(1):1-5.)
[11] ZHANG Yong.Research and Application of the Vertical LinesSupported Aerial Triangulation[D]. Wuhan: Wuhan University,2006.(张勇.铅垂线辅助空中三角测量的应用研究[D].武汉:武汉大学,2006.)
[12] ZHANG Yong,DAI Teng,XIAO Weiwei,et al.Application of Nadir Constraints in Aerial Triangulation over Urban Areas[J].Bulletin of Surveying and Mapping, 2008,12:18-21.(张勇,戴腾,肖巍巍,等.像底点约束在城市大比例尺空三中的应用[J].测绘通报,2008,12: 18-21.)
[13] LI Deren,ZHENG Zhaobao.Analytical Photogrammetry [M]. Beijing:Publishing House of Surveying and Mapping,1992.(李德仁,郑肇葆.解析摄影测量学[M].北京:测绘出版社,1992.)
[14] BÄUMKER M,HEIMES F J.New Calibration and Computing Method for DirectGeoreferencing of Image and Scanner Data Using the Position and Angular Data of an Hybrid Inertial Navigation System[J].Integrated Sensor Orientation,2002,43:197-212.
[15] Applanix Product Outline.POSPaTMAir[EB/OL].[2011-02-19].http:∥www.applanix.com/products/airborne/ pospac-mms.html.
[16] FU Jianhong.Research on Calibration Field Designing for Airborne Position and Orientation System[C]∥Proceeding of SPIE:7498.Bellingham:SPIE,2009:749803-749803.
