基于移不变全方向角提升的遥感图像降噪

王晓甜,石光明,牛 毅,矫恒浩,2

1.西安电子科技大学电子工程学院智能感知与图像理解教育部重点实验室,陕西西安710071;2.大唐移动通信有限公司产品测试部,陕西西安710071

1 引 言

遥感卫星成像是对地观测的重要手段之一,在国家安全、国民经济、科学研究和人民生活等方面有重要作用。随着军事信息化发展、民用勘测要求的日益提高和高分辨率成像系统的出现,遥感图像要尽可能逼真的反映所观测的地形、地貌甚至小目标,如道路、桥梁和建筑物等,而噪声的存在给实现这一目标带来极大困难。因此,在遥感图像的处理中,对噪声的抑制是一个受到广泛关注的问题[1-3]。

图像去噪研究的关键所在就是寻找图像信号与噪声之间的不同特点,并利用这些特点将它们区分开。在二维图像信号中,边缘和纹理是对图像进行分析和理解的一个极其重要的信息源,是图像信号区别于噪声的基本特征之一。遥感图像中含有大量的边缘信息,它们往往代表许多重要的、详细的地质信息,如道路和桥梁等建筑的边缘和纹理。这些边缘和纹理是军事作战及民用勘测极为重视的图像信息,因此如何在有效去除图像噪声的同时保留图像边缘细节和纹理信息不被破坏或模糊是遥感图像去噪领域的研究热点。

二维小波变换是近年来广泛应用的图像信号处理工具。提升结构是小波变换的简化实现方式,通过因式分解将小波变换中的滤波器卷积运算转化为若干简单的预测和更新步骤,实现了低运算量原位运算的可并行处理框架,使以小波变换为基础的星载实时图像处理系统的实现成为可能。无论是二维小波还是二维提升,都由水平和竖直变换交替进行实现。它们能优化表示的图像纹理方向仅局限于水平,竖直和斜45°方向。然而二维图像具有纹理丰富和边缘方向多变等特点,存在局部非平稳和各向异性。特别是在星载遥感图像中,这种非平稳和各向异性表现尤为明显。小波和传统提升难以满足复杂结构遥感图像分析的需求。

近年来国际上广泛应用的方向提升小波(ADL)由于其良好的对图像边缘和纹理的优化表示能力,已被成功应用于图像压缩和插值领域[4-6]。近期研究表明ADL的方向选择特性也可以被应用于图像去噪领域[7-9]。ADL可以将图像的边缘和纹理尽可能的压缩到低频子带,将噪声产生的没有方向性的高频信息留在高频子带,从而实现将图像的纹理和噪声在小波域更好的分开。通过阈值策略对高频系数进行处理,就可以实现在去噪的过程中尽可能地保留图像边缘信息,达到更好的去噪效果[7-9]。

然而ADL应用于图像去噪存在三个需要解决的问题:①基于拉普拉斯塔式变换的提升结构致使提升变换的小波基缺乏移不变性质,因而在去噪过程中会引入吉布斯效应,破坏视觉效果;②方向提升中的局部方向信息判断方法缺乏噪声鲁棒性,因而在含噪环境中判断准确性下降,准确的变换方向是ADL将信号产生的高频分量压缩到低频子带的前提,错误的变换方向会严重影响去噪性能;③由于受到变换结构的限制,ADL能够优化表示的边缘方向局限在90°之内,对于不属于该方向区间内的边缘和纹理无法优化表示。

为了克服以上缺点笔者提出基于移不变全方向角提升小波(TI-OL)的去噪方法并将其应用于遥感噪声处理领域。利用ADL对边缘和纹理的良好的表示性能,将图像和噪声在小波域更好的分开,从而实现去噪的同时保护边缘和纹理信息的目的。该方法采用循环平移[10]和 Gabor小波滤波器[11]克服ADL的前两个缺点。对于第三个缺点,利用方向判断的结果和图像旋转技术确保图像纹理方向始终保持在图像优化变换方向区间内。试验结果证明本文方法在去噪效果和边缘保留性能方面跟ADL相比有较大提升,与现有经典技术如移不变小波(TI-WT),和 non-local means相比也在客观评价(PSNR)和主观视觉效果(SSIM)上有一定程度的提高。

2 自适应方向提升小波(ADL)

ADL构建于传统提升小波变换框架之上,继承了传统提升结构简单、可以实现原位运算、并行处理和便于逆变换的特点,并在变换过程中引入图像局部方向信息,克服了传统提升方向分辨率过低的缺点。不同于传统提升交替进行竖直和水平变换,ADL分析图像的局部方向信息,并使每一个提升步骤都沿着图像局部像素相关性最高的方向进行变换,实现局部最大去相关性,将图像中边缘和纹理产生的高频信息尽可能的压缩到低频子带,从而克服了传统小波缺乏灵活的方向选择性的缺点。

在传统提升中,每个提升步骤中的预测(或更新)系数来自被预测(或更新)点的竖直或水平相邻像素。以图1所表示的竖直变换为例,当x[m, n]为被预测点时,预测系数仅来自其竖直方向的相邻行整数位置像素,即 x[m±i,n],如式(1)所示

式中,x0[m,n]为图像奇相位像素集合;xe[m,n]为图像偶相位像素集合;d[m,n]为预测高频残差;c[m,n]为低频逼近系数;为预测算子;为更新算子;pi和uj分别为预测系数和更新系数。

二维图像信号中的边缘具有较强的局部相关性,非平稳性和各向异性。而噪声是服从一定分布的随机点状干扰,它属于非平稳信号,但它与周围像素没有相关性,服从各向同性分布。传统小波在去噪过程中仅利用了图像信号具有较强相关性,而忽略了边缘和纹理的方向特性。二维信号沿着边缘和纹理的法线方向变换会得到高频信息,沿着边缘和纹理的切线走向变换则会得到低频信息,而沿着任意方向进行变换,噪声都是高频信息。如果能使提升始终沿着边缘和纹理的切线方向进行预测和更新,就能将信号的边缘和纹理信息都压缩到低频子带,将噪声留在高频子带,从而实现在小波域将图像信号和噪声在小波域更好的分开。

不同于传统提升,ADL的预测和更新沿着图像局部纹理的方向,而不是竖直、水平方向交替进行[4-7]。如图1,图中“·”为实际存在的整数位置像素,“＊”和“+”分别为利用自适应插值得到1/4和1/2位置像素。ADL利用插值算法插出分数点像素,并分析图像纹理方向 dir,选取预测残差最小的方向作为变换方向。

图1 方向提升小波变换方向Fig.1 Possible directions exist in the vertical transform

ADL的预测和更新算子如式(2)所示

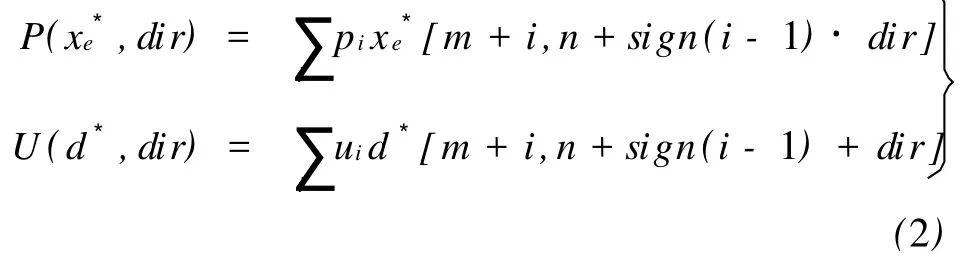
式中,dir为图像当前块内的纹理方向;x＊e[m,n]是 xe[m,n]的插值结果;d＊[m,n]是 d[m,n]的插值结果。ADL的变换流程图如图2所示。

ADL在变换过程中解决了传统提升变换方向有限的问题,实现了对边缘和纹理等高频分量达到更好的去相关性,将更多图像信号产生的高频分量压缩到低频子带,从而在高频子带只留下没有方向信息的噪声产生的高频分量。如图3所示[7],图3(a)为充满纹理的标准测试图,图3(b)为用传统提升对测试图进行小波变换的高频子带,图3(c)为用ADL对测试图进行变换的高频子带。可以看出,在传统提升的变换结果的高频子带中,仍残留了大量图像纹理产生的高频信息,因此对高频系数的阈值处理必然会影响到图像的纹理信息。而通过ADL变换,有图像信号产生的高频信息已经被压缩到低频子带中(如图3(c)),通过对含噪信号的高频变换子带(图3(d))进行阈值处理,就可以实现在有效去除噪声的同时更好的保留图像边缘信息。

图2 方向提升小波变换流程Fig.2 Adaptive directional lifting transform scheme

图3 对测试图像进行一级分解的高频子带Fig.3 Testing image and its one level decomposition HH band

3 移不变全方向角提升小波变换

如前所述,尽管ADL在图像处理领域取得了一定的成果,但在图像去噪方面,ADL存在三个固有的缺点:缺乏移不变性质,图像局部方向信息判方法断缺乏鲁棒性和变换方向分布有限。本节将具体分析这三个问题并讨论解决方法。

3.1 基于循环平移的移不变方向提升小波

构建于传统提升基础之上的ADL在继承传统提升结构简单,可实现原位运算等优点的同时,也继承了传统提升小波基缺乏移不变特性的缺点。缺乏移不变特性在去噪过程中会给图像信号不连续位置带来振铃效应,也就是众所周知的吉布斯现象[8,10]。吉布斯现象严重影响去噪结果的客观评价性能和主观视觉效果。根据文献[10]的研究表明,吉布斯现象的出现与图像信号不连续的实际位置有很大关系,通过对下采样后的所有相位进行变换和去噪并取所得结果的平均值可以有效地避免吉布斯现象。因此本文采用循环平移方法来消除去噪结果中出现的振铃效应。

在二维信号软阈值去噪过程中,基于循环平移处理的移不变提升的去噪算法结构如式(3)所示

式中,x是含噪图像;^s是去噪图像;M是平移次数;L是提升过程;T为阈值处理;Si,j是时移操作。

3.2 基于2-D G abor wavelet滤波器的图像局部方向信息判断方法

图像纹理方向判断的准确性是决定ADL性能的前提。以图1为例,方向提升判断图像局部纹理方向的方法如式(4)所示

式中,i=1,2,…,9,fi是第i个方向的预测残差系数。该方法遍历9个方向各进行一次预测,取预测残差最小的方向作为变换方向。可以看出,能够预测出的图像方向仅局限于45°～135°。当图像纹理方向属于-45°～45°时,ADL无法准确判断出该方向,仍采用45°～135°内预测残差最小的方向来逼近图像,如图4(a)所示,所有预测出的局部块方向都在45°～135°内。另一方面,这种方法以高频预测残差的大小作为依据判断图像局部方向,在有噪声干扰的情况下这种方法的判断结果准确性急剧下降,如图4(a),方向判断仅在图像纹理特性强的区域能得到准确的判断结果。

图4 图像局部方向判断Fig.4 Image local orientation estimation

为了克服以上缺点,本文采用2-D Gabor小波生成方向滤波器[8,11],来获取图像局部方向信息。由二维傅里叶分析可知,图像的纹理方向与图像的主频谱线方向是正交关系[12]。因此,用如图4所示的方向滤波器对图像进行滤波,与子带能量最大的方向垂直的方向即为图像局部纹理方向。Gabor小波函数如式(5)所示

g(x,y)可以被视为母小波。通过对式(5)进行适当的尺度伸缩和方向旋转,可以得到一组2-D Gabor小波滤波器,如图5(a),是尺度为5,方向因子为16的 2-D Gabor小波滤波器频谱图。图5(b)为该方向滤波器进行方向判断的时域分割图,其中,空心圆圈为整数位置像素。

图5 2-D Gabor小波滤波器Fig.5 2-D Gabor wavelet filters

图4(b)为采用本文方法进行方向判断所得的结果。基于方向滤波器在频域进行方向判断具有较高的噪声鲁棒性,并且能判断出180°方向内的所有16个方向,克服了ADL方向判断结果局限在45°～135°的缺点。

3.3 基于图像旋转的优化方向变换

如前文所述,ADL虽然比传统提升有更灵活的方向选择性能,但是由于受到提升结构的限制,其变换方向局限于45°～135°(以竖直变换为例)[9],如图1所示。参照图5(b)的空间方向分布图所表示的16个方向,ADL能够优化表示的图像边缘和纹理仅局限于方向1～9。当图像局部纹理存在于-45°～45°(方向10～16)时,ADL则无法对该边缘进行优化表示,只能用45°～135° (方向1～9)内预测残差最小的方向作为近似优化的方向对其进行逼近。这样的近似必然影响逼近效果。为了更直观地显示变换方向对去噪结果的影响,以Barbara的裤子部分纹理区域为例,图6(a)为Barbara左腿裤子的纹理区域,其纹理方向存在于45°～135°内,图6(g)为对图6(a)进行90°旋转,纹理方向存在于-45°～45°。图6(b)与图6(h)为分别对6(a)与图6(g)加入σ=20的高斯白噪声的含噪图像,PS N R=21.56 dB。图6 (c)与图6(i)为用ADL判断出的变换方向,可见,当图像纹理存在于45°～135°时(图6(c)),ADL能够准确判断纹理方向,并沿着该方向进行方向提升变换。对变换后的系数进行阈值处理可以在去除噪声的同时有效保留图像纹理细节信息,如图6(d)(PS N R=25.32 dB)。当图像局部纹理方向属于-45°～45°时,ADL只能用45°～135°内最接近图像纹理方向作为变换方向(图6(i)),取得对纹理信息的近似逼近。这样的近似不能有效地达到去除信号相关性的目的,变换后的高频系数中仍留有一定信号纹理产生的高频分量并与噪声混杂在一起,在高频分量中进行的阈值处理会直接影响图像纹理信息。图6(j)为方向提升对图6(h)的去噪结果 (PS N R=24.78 dB),可以看出去噪结果的图像信息受损,纹理之间有明显扰动。图6(d)与图 6(j)的图像质量客观评价也有0.5 dB左右的差别。

图6 提升方向对去噪结果的影响Fig.6 Lifting direction and denoising results

提升方向的准确性对去噪结果有着直接并且显著的影响。然而,ADL的方向区间有限,无法保证对图像任意方向边缘和纹理都做到优化近似。为了克服这一缺点,笔者利用 Gabor小波方向滤波器判断出的结果来修正变换方向。如前所述,方向滤波器可以判断出并且能判断出180°方向内的所有16个方向(考虑到图像纹理和边缘的方向没有二向性,即45°方向与225°为同一方向,所以二维平面上的纹理所有方向可以用180°内的方向角完全表示)。方向判断结果如图6(e)和图6(k)所示。ADL以块为单位进行变换,当判断出图像当前块的纹理属于-45°～45°时,对其进行先转置,以使其纹理方向属于45°～135°,再进行变换,如

式中,(·)＊是转置操作;s是当前处理的图像块; ^s为去噪恢复出的图像块;L为提升操作;L-1为提升逆变换;T为提升系数阈值处理操作。f lag为图像块纹理方向分类标志,当图像纹理属于45°～135°时,f lag=0,当图像纹理属于-45°～45°时,f lag=1。

对纹理方向属于-45°～45°的图像块先旋转再变换,可以将图像纹理旋转至ADL能够优化表示的方向区间内,从而得到与纹理方向属于45°～135°内的图像块效果相同的去噪图像。如图6(l)为采用本文方法对纹理属于-45°～45°内的图像块的去噪结果,由试验结果可见,本方法弥补了传统方向提升能够优化表示的方向有限的缺点,处理各个方向的纹理信息都能达到同样的优化表示的性能。

4 试验结果及分析

为了验证本文提出的去噪算法,对两幅遥感图像air1(图7(a))和air2图7(b))分别进行了加噪和去噪的仿真处理并展示去噪结果。普通成像系统的去噪算法分析去噪结果大都针对零均值高斯白噪声。然而,根据遥感图像成像系统的工作原理特性分析可知,存在于遥感图像中的噪声主要有两种模型:服从高斯分布的读出噪声和服从泊松分布的光电散粒噪声。在实际的卫星成像系统中,这两种噪声叠加混杂在一起,形成高斯-泊松混合噪声[16]。因此本文分别对这两类噪声模型进行去噪仿真试验,并分析去噪结果。本文试验中生成两组含噪图像,一组为加入均值为0, σ=20的高斯白噪声的含噪图像g_air1和g_air2 (图7(c),(d));一组为加入服从高斯-泊松联合分布噪声的含噪图像gp_air1和gp_air2(图7(e), (f)),并分别对它们进行去噪处理。

图7 试验用遥感图像Fig.7 Remote sensing images for experiments

在仿真试验中,采用双正交Debauches 9/7滤波器组来实现提升变换,在对高频系数的处理过程中,采Bivariate-Shrinkage[13]阈值处理算法。为了突出本算法遥感图像噪声处理过程中的性能优势,还对比了现有的几种经典去噪算法如nonlocal means1http:∥www.cs.berkeley.edu/～brox/code.html(NLM)[14],移不变小波变换2http:∥www-stat.stanford.edu/～wavelab(TIWT)[10]以及本文所改进的方向提升小波变换(ADL)[7]的去噪结果。采用峰值信噪比 PSNR作为去噪结果的客观评价,采用感知结构相似度质量指标 (perceptual quality index structural similarity(SSIM))[15]作为对去噪结果的主观视觉评价标准。

表1和表2分别为各种算法对遥感图像处理结果的PSNR和SSIM比较。由表中数据结果比较可见,本文方法在峰值信噪比和结构相似度方面较传统算法都能取得性能上的提高。

表1 去噪结果PSNR比较Tab.1 PSNR statistics for different method dB

表2 去噪结果SSIM比较Tab.2 SSIM statistics for different method

为了突出显示去噪结果的视觉效果,图8显示了对高斯白噪声污染的遥感图像air1进行处理结果的局部纹理部分,图9显示了对高斯-泊松混合噪声污染的遥感图像air2处理结果的局部纹理部分。比较结果图可以看出,传统方向提升虽然能突出图像的边缘和纹理,但由于缺乏移不变特性而引起明显的振铃效应直接影响去噪效果。基于移不变小波变换的去噪方法消除了振铃效应,但由于其缺乏灵活的方向选择性能,无法优化表示图像边缘和纹理,导致去噪结果的道路,桥梁和房屋边缘信息受损。Non-local means方法的去噪结果可以较好的平滑噪声,但是存在过平滑问题,容易损坏图像的边缘细节信息。而本文提出的去噪算法结合了传统方向提升和移不变小波的优点,在平滑噪声的同时能够较好地保留图像的边缘纹理等细节信息,达到更好的主观视觉效果。

图8 受高斯白噪声污染air1局部区域去噪结果Fig.8 Denoising result of a part of air1 contaminated by Gaussian noise

图9 受高斯-泊松混合噪声污染air2局部区域去噪结果Fig.9 Denoising result of a part of air2 contaminated by Gaussian-Poisson noise

5 结 论

本文提出一种基于移不变全方向角提升小波去除遥感图像噪声的方法。该方法继承了方向提升小波灵活的方向选择性,并解决了方向提升小波应用于图像去噪过程中存在的缺乏移不变性质,图像局部方向信息判方法断缺乏鲁棒性和变换方向分布有限这三个缺点。本方法应用于存在大量边缘和纹理等细节信息的遥感图像去噪中,能够在有效消除噪声的过程中,较好地保留图像信息,去噪结果取得了优于传统方法的客观评价和主观视觉效果。

[1] WANG Zhiwu,DING Guoqing,YAN Guozheng,et al. Adaptive Lifting Wavelet Transform and Image Denoising [J].Journal of Infrared and Millimeter Waves,2002,21 (6):447-450.(王志武,丁国清,颜国正,等.自适应提升小波变换与图像去噪[J].红外与毫米波学报,2002,21 (6):447-450.)

[2] WANG Xianghai,ZHANG Hongwei,LI Fang.A PDE-based Hybrid Model for De-noising Remote Sensing Image with Gaussian and Salt-pepper Noise[J].Acta Geodaetica et Cartographica Sinica,2010,39(3):283-288.(王相海,张洪为,李放.遥感图像高斯与椒盐噪声的PDE混合去噪模型研究[J].测绘学报,2010,39(3):283-288.)

[3] SONG Yingchun,LIU Qingyuan,ZENGLianbin,et al.An Algorithm for Kinematic Filtering with Contaminated Measurement Noises[J].Acta Geodaetica et Cartographica Sinica,2009,38(2):138-143,151.(宋迎春,刘庆元,曾联斌,等.测量噪声污染时的一种动态滤波算法[J].测绘学报,2009,38(2):138-143,151.)

[4] DING Wenpeng,WU Feng.Adaptive Directional Lifting Based WaveletTransform for Image Coding[J].IEEE Transaction on Image Processing,2007,16(2):416-684.

[5] LIU Yu,KING N N.Weighted Adaptive Lifting-based WaveletTransform[J].IEEE Transaction on Image Processing,2008,17(4):500-511.

[6] DONG Weisheng,SHI Guangming,XU Jizheng.Signaladapted Directional Lifting Scheme for Image Compression [C]∥Proceedings of IEEE International Symposium on Circuits and Systems(ISCAS’08).Seattle:[s.n.],2008: 1392-1395.

[7] WANG Xiaotian,SHI Guangming,NIU Yi,et al.Robust Adaptive Directional Lifting Wavelet Transform for Image Denoising[J].IET Image Process,2011,5(3):249-260.

[8] WANG Xiaotian,SHI Guangming,LIANG Lili.Image Denoising Based on Translation InvariantDirectional Lifting[C]∥Proceedings of IEEE International Conference on ICASSP.Dallas:[s.n.],2010:1446-1449.

[9] JIAO Henghao,The Adaptive Directional Lifting-based Wavelet Transform for Image Denoising and Its Implementation[D].Xi’an:Xidian University,2009.(矫恒浩.自适应方向提升小波图像去噪及其实现[D].西安:西安电子科技大学,2009.)

[10] COIFMAN R R,DONOHO D L.Translation Invariant Denoising,Wavelets and Statistics[J].Springer Lecture Notes in Statistics 1994,103:125-150.

[11] BOVIK A C,CLARK M,GEISLER W S.Multichannel Texture Analysis Using Localized SpatialFilters[J]. IEEE Transaction on Pattern Analysisand Machine Intelligence,1990 12(1):55-73.

[12] SHI Guangming,WANG Xiaotian,ZHANG Li,et al. Removal of Random Stripe Noises in Remote Sensing Image by Directional Filter[J ].Journal of Infrared Millimeter Waves,2008,27(3):214-318.(石光明,王晓甜,张犁,等.基于方向滤波器消除遥感图像孤立条带噪声的方法[J].红外与毫米波学报,2008,27(3):214-318.)

[13] SENDUR L,SEL ESINCK I W.Bivariate Shrinkage Functions for Wavelet-based Denoising[J].IEEE Transaction on Signal Processing,2002,50(11):2744-2756.

[14] BROX T,KLEMSCHMIDT O,CREMERS D.Efficient Nonlocal Means for Denoising of Textural Patterns[J]. IEEE Transaction on Image Processing,2008,17(17): 1083-1092.

[15] WANG Zhou,BOVIK A C,SHEIKH H R,et al.Image Quality Assessment:from Error Visibility to Structural Similarity[J].IEEE Transaction on Image Processing, 2004,13(4):600-612.

[16] ZHU Shulong,ZHANG Zhanmu.Remote Sensing Image Acquisition and Analysis[M].Beijing:Science Technology Press,2000.(朱述龙,张占睦.遥感图像获取与分析[M].北京:科学技术出版社,2000.)