孔径为4的全球六边形格网系统索引方法

贲 进，童晓冲，元朝鹏

1.信息工程大学测绘学院，河南郑州450052；2.西安测绘信息技术总站，陕西西安710054

1 引 言

全球离散格网数据模型的基本思想是将地球递归剖分为形状、面积近似相等且具有规则层次结构的单元，每个单元在记录位置信息的同时也表达比例尺和精度，因而具有处理多尺度数据的潜力。同一剖分产生的一系列不同分辨率的格网称为“格网系统”，按照数学基础的不同，可将其划分为基于地理坐标系的全球离散格网系统和基于多面体剖分的全球离散格网系统。

地理坐标系是最常使用的球面坐标系，在此基础上建立的经纬格网系统得到广泛应用。这类格网系统大都存在高纬地区单元变形严重的缺陷，而且矩形格网单元临近关系的定义并不严格［1］。基于多面体剖分的全球离散格网系统是经纬格网的推广，在空间分析、元胞自动机、气候模拟等方面均有应用［2－4］。

与经纬格网相比，基于多面体剖分的全球离散格网系统具有以下优势：① 以整个地球为研究对象且两极不存在畸变，更适合处理全球尺度的问题；② 对地球表面同构离散化，有助于数据统一建模和重组；③ 格网具有层次性，在结构上支持多尺度数据表达；④ 空间运算可以采用编码运算完成，更适合计算机处理。

2 六边形格网系统

在构建格网常用的3种几何图形或剖分方法（三角形、四边形和六边形）中，六边形格网的空间覆盖效率和角度分辨率最高，单元一致相邻且无共顶点的角邻近单元，这些特性都有利于空间数据的处理和分析［1］。

然而，六边形全球离散格网系统的相关问题一直都是学术界的研究难点，这是因为：① 六边形不具备自相似性，一个大六边形不能完全分解为若干小六边形，导致不同分辨率格网之间的层次关系描述困难；② 采用六边形不能完全覆盖全球，在多面体顶点处必然出现其他形状的单元，需要分别处理；③ 六边形剖分的方法较多，几乎不可能建立适合各种情况的“统一剖分模型”，只能分别讨论。

孔径（aperture），即相邻层次格网单元的面积之比，是描述格网系统或剖分方法的重要指标。孔径越小，相邻层次格网的分辨率变化越均匀，对多分辨率应用越有利。六边形剖分的最小孔径是3（图1），许多学者对这类格网系统进行了较深入的研究。文献［5—6］将平面上的广义平衡三进制（general balanced ternary，GBT）扩展到球面，提出基于正二十面体的六边形格网编码、索引算法；文献［7—8］从理论上证明采用平衡三进制（balanced ternary，BT）可有效描述基于正八面体的六边形格网层次关系；文献［9］采用复平面的向量组合建立基于正二十面体的六边形格网编码方案；文献［10］研究基于正二十面体的六边形格网三角化算法。孔径为3的六边形格网系统存在的主要不足是单元的方向随剖分层次交替变化，这导致相关算法较复杂。

图1 孔径为3的六边形格网系统Fig.1 The aperture 3hexagonal grid system

孔径为4的六边形剖分方法不唯一，对应的格网系统均具有单元方向固定、层次结构简单的优点。图2是典型的孔径为4的六边形剖分，每个单元仅有1或2个父单元，这一特性有助于建立高效的格网索引。但是，目前学术界对这类格网系统的研究尚不深入。

图2 孔径为4的六边形格网系统Fig.2 The aperture 4hexagonal grid system

以基于正八面体的、孔径为4的六边形格网系统（octahedron－based aperture 4hexagonal discrete global grid system，OA4HDGGS）为研究对象，从集合论的角度建立不同层次六边形格网和三角形格网之间的递推关系，借助三角形单元顶点建立六边形单元层次关系并据此设计单元索引算法，通过对比试验验证该方法的效率。

3 OA4HDGGS的数学描述

从集合论的角度思考，格网系统是一系列不同分辨率格网的集合，也是一些单元的集合。尽管直接描述OA4HDGGS有难度，但是六边形可以分解为三角形，能够建立三角形格网集合之间的关联就相当于建立了六边形格网集合之间的关联，这是描述OA4HDGGS的基本思想。为简化表达，下文出现的符号及其约定见表1。

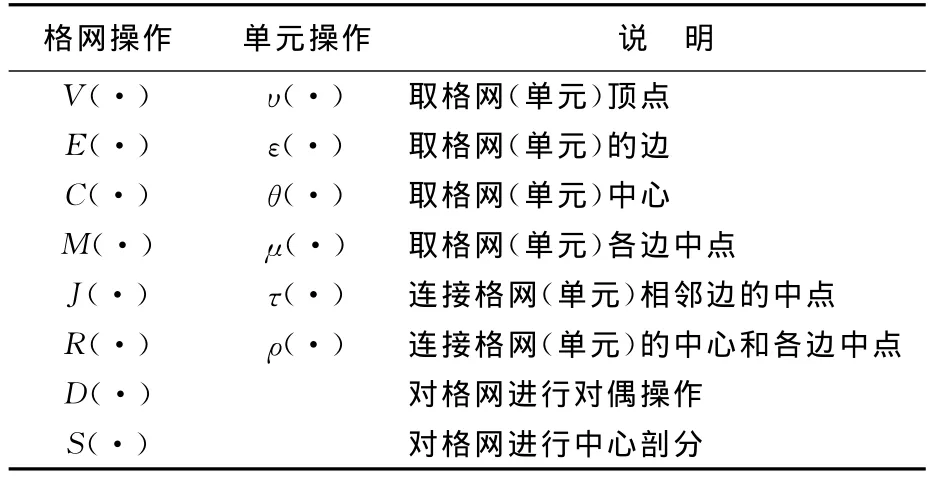
表1 符号约定Tab.1 The convention of signs

设正八面体中心和单位球（半径为1）球心均在R3的原点，在正八面体表面或球面取顶点坐标为（x1，x2，x3）的三角形单元t的中心，即

取三角形格网T中所有单元的中心构成一个集合，记为C（T）＝｛θ（t）｜t∈T｝。

在正八面体表面或球面，取顶点坐标为（x1，x2，…，x6）的六边形单元h的中心，即

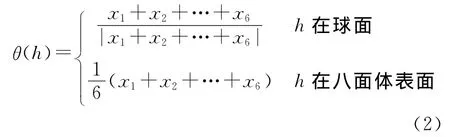
h边的集合记为ε（h），取任意一边e（xi，xi＋1）（i＝1，2，…，5）的中点，记为

相邻各边中点连线构成的集合记为τ（h），即τ（h）＝｛l［μ（ei），μ（ei＋1）］｜ei∈h，ei＋1∈h｝，l［μ（ei），μ（ei＋1）］表示端点为μ（ei）、μ（ei＋1）的线段，下同。

h中心和各边中点的连线构成的集合记为ρ（h），即ρ（h）＝｛l［θ（h），μ（ei）］｜ei∈h｝。取六边形格网H中所有单元边的中点构成一个集合，记为M（H）＝｛μ（h）｜h∈H｝。连接H中所有单元边的中点构成一个集合，记为J（H）＝｛τ（h）｜h∈H｝。连接H中所有单元的中心和边的中点构成一个集合，记为R（H）＝｛ρ（h）｜h∈H｝。为了建立三角形格网T和六边形格网H之间的关联，定义如下操作，如图3。

图3 格网上的操作示意图Fig.3 Operations on grids

（1）对偶。对偶操作D（T）的顶点集合V［D（T）］＝C（T），当且仅当T中对应单元共用一条边时，D（T）中两个顶点之间有边连接。

（2）中心剖分。中心剖分S（H）的顶点集合记为V［S（H）］＝C（H）∪M（H），S（H）边的集合E［S（H）］＝R（H）∪J（H）。

在球面或八面体表面定义集合序列（Tn，Hn）（前4层如图4）：T0是位于R3原点的正八面体或其在球面上的映射；格网集合序列递归定义为

式中，Hn即OA4HDGGS，n≥1是剖分层次。

采用数学归纳法不难证明如下结论：① 三角形格网Tn共有2×9×4n个单元；②格网Hn中共9×4n－4有个六边形单元，顶点处共有6个四边形单元；③Tn的顶点集合Vn∶＝V（Tn）严格满足V0⊂V1⊂V2⊂…⊂Vn；④Hn的中心集合Cn∶＝C（Hn）严格满足H0⊂H1⊂H2⊂…⊂Hn；⑤h∈Hn与Hn＋1中7个单元相交，其中有1个中心子单元，6个邻近子单元；⑥h∈Hn与Hn－1中1个或2个单元相交，当h是中心子单元时是1个单元，当h是邻近子单元时是2个单元，这些n－1层上的单元称为h的父单元。

图4 （Tn，Hn）在单个三角面上的示意图Fig.4 （Tn，Hn）on a single triangular face

4 OA4HDGGS的单元索引算法

设t∈T0的顶点位于R3中（±1，0，0）、（0，±1，0）、（0，0，±1），h∈Hn的笛卡儿坐标不是整数，这给单元快速索引造成不便。为了解决这一问题，建立三轴格网坐标系，其单元坐标h（a，b，c）均为整数（图5）。在三轴格网坐标系下，Hn满足如下定理（具体证明与文献［8］类似，本文不再赘述）。

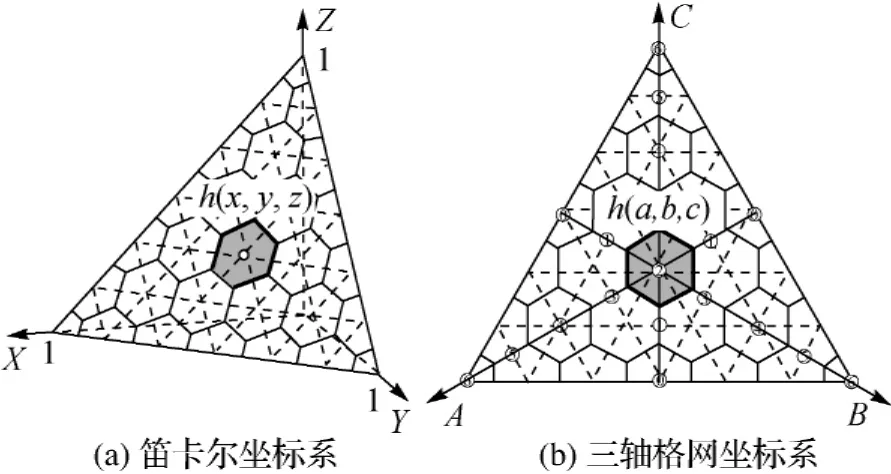
图5 坐标系的定义Fig.5 Definitions of coordinate systems

定理1：h∈Hn中心（t∈Tn顶点）的格网坐标满足是h在R3中的坐标。

例如，h（2，2，2）∈H2满足2＋2＋2＝3× 22－1＝6，其笛卡儿坐标

该定理不仅建立了格网坐标系和笛卡儿坐标系之间的联系，而且也说明（a，b，c）与Hn的单元一一对应。

定理2：当且仅当Vn∶＝V（Tn）中两顶点A（a1，a2，a3）和B（b1，b2，b3）满足｜ai－bi｜≤1（i＝1，2，3）时，A、B两点之间有边相连。

例如，对A（2，2，2）∈T2满足定理2的顶点有：B1（1，3，2）、B2（1，2，3）、B3（2，1，3）、B4（3，1，2）、B5（3，2，1）、B6（2，3，1），它们在T2中和A均有边相连。

再如，对A（0，0，6）∈T2满足定理2的顶点有：B1（1，0，5）、B2（0，1，5）、B3（－1，0，5）、B4（0，－1，5），它们在T2中和A均有边相连。

该定理表明Hn中一个六边形单元有6个邻近单元，一个四边形单元（位于八面体的6个顶点上）有4个邻近单元。

定理3：hA（a1，a2，a3）∈Hn的邻近单元hB（b1，b2，b3）可表示为｜ai－bi｜≤1（i＝1，2，3）。

例如，hA（2，2，2）∈H2的邻近单元是：hB1（1，3，2）、hB2（1，2，3）、hB3（2，1，3）、hB4（3，1，2）、hB5（3，2，1）、hB6（2，3，1），其格网坐标满足定理3。

因为Tn的顶点即Hn的单元中心，所以定理3与定理2等价。

定理4：h（a，b，c）∈Hn在Hn＋1上的中心子单元是h′（2a，2b，2c），当且仅当a、b、c同为偶数时，h（a，b，c）是中心子单元，其在Hn－1上的父单元是

例如，h（2，2，2）∈H2在H3上的中心子单元是h′（4，4，4），h是的中心子单元，满足定理4。

该定理描述了中心子单元的层次关系。

定理5：设h（a，b，c）∈Hn是邻近子单元，则h有2个邻近单元h′（d，e，f）的格网坐标全是偶数，h在Hn－1上父单元是

例如，h（1，3，2）∈H2是邻近子单元，根据定理3，h的邻近单元是：h1（0，4，2）、h2（0，3，3）、h3（1，2，3）、h4（2，2，2）、h5（2，3，1）、h6（1，4，1），其中h1和h4两个单元的格网坐标全是偶数，h在H1上有和个父单元。满足定理5。

该定理描述了邻近子单元的层次关系。

一般来说，离散全球格网上的基本索引操作包括：① 查找某一单元的邻近单元；② 查找某一单元的子单元；③ 查找某一单元的父单元。在定理1～5的支撑下，很容易设计出OA4HDGGS上的单元索引算法。根据定理3，可计算出h（a，b，c）∈Hn的邻近单元；根据定理3和定理4，可计算出h（a，b，c）∈Hn在Hn＋1上的中心子单元和邻近子单元；根据定理4和定理5，可计算出h（a，b，c）∈Hn在Hn－1上的父单元。

在算法实现过程中，可采用“编码压缩”技术以节省数据存储空间。在区间［－2m－1，2m－1）内的任意整数都可以用m个二进制位表示。对于h（a，b，c）∈Hn，因为a、b、c≤3×2n－1，所以每个坐标需要用n＋1个二进制位记录。又根据定理1，c＝±（3×2n－1－｜a｜－｜b｜），因此在准确记录a、b的前提下，只需再用一个二进制位记录c的正负即可。这样共需2n＋3个二进制位对Hn中的单元进行编码。在32位Windows XP操作系统上，如果直接采用内置的int64整数类型，能够支持30层格网的编码，此时单元分辨率已达到毫米级，对于地球空间信息的表达和处理已足够。

在上述索引算法中，邻近单元查找只涉及整数（二进制数）的自加、自减运算，在计算机中的执行效率较高。父（子）单元查找也只涉及整数（二进制数）的2倍数运算，可通过位运算实现，执行效率更高。

5 对比试验与分析

为了验证上述索引算法的可行性和优越性，将其与文献［8］提出的基于BT的索引算法进行对比。

第一组试验首先在正八面体第一卦限的三角面上进行指定层次（5～18）、孔径为3的六边形剖分，包括三角面边界和顶点上的单元，第n层格网上的单元数目是（n是奇数）是偶数）。然后采用BT算法查找该层次上每个单元的邻近单元、子单元和父单元，统计平均执行效率。BT的转换及运算采用文献［11］中的算法实现。

第二组试验在同一三角面上进行指定层次（5～18）、孔径为4的六边形剖分，包括三角面边界和顶点上的单元，第n层格网上的单元数目是（3·2n＋2）（3·2n＋4）。然后采用本文的索引算法进行查找并统计平均执行效率。

所有程序均在Windows XP SP3系统上采用Visual C＋＋2008SP1编译成Release版本后在一台兼容机（处理器Intel Pentium Dual 3.0GHz；内存1.0GB DDR2－667SDRAM）上运行，结果如表2、图6、图7所示。

通过以上对比试验不难发现，本文的索引算法与BT算法相比具有明显优势：首先，执行效率非常高，平均约是BT算法的600倍（表2）；其次，执行效率稳定（图6），而BT算法的效率随格网层次的增加急剧下降（图7）。

造成以上现象的根本原因在于本文索引算法可以完全采用加减、移位等执行效率极高的基本操作实现，而在计算机中没有与BT对应的数据类型，只能通过数组、结构等模拟其运算，导致BT索引算法效率较低。

表2 试验结果（10层～18层）Tab.2 The result of experiments（level 10～level 18）

图6 本文算法的效率曲线Fig.6 The efficiency curves of our algorithms

图7 BT算法的效率曲线Fig.7 The efficiency curves of BT algorithms

6 结 论

采用编码代替浮点数进行运算是全球离散格网数据模型的特色之一，因此单元编码方案和对应索引算法的设计非常重要。基于正八面体的、孔径为4的六边形离散全球格网的几何性质，提出一种索引方法。与现有成果相比，这种编码索引方案的优点体现在：① 采用集合论描述格网剖分，理论基础严密，表达形式简洁；② 建立了三角格网和六边形格网之间的关联，便于格网的三角化显示；③单元编码与其空间坐标的对应关系简单，转换方便；④ 单元层次、邻近关系明确，索引算法简单高效。

［1］ SAHR K，WHITE D，KIMERLING A J.Geodesic Discrete Global Grid Systems［J］.Cartography and Geographic Information Science，2003，30（2）：121－134.

［2］ CHEN Jun，HOU Miaole，ZHAO Xuesheng.Describing and Computing Model of the Topological Relation in Spherical Surface Quaternary Triangular Mesh［J］.Acta Geodaetica et Cartographica Sinica，2007，36（2）：176－180.（陈军，侯妙乐，赵学胜.球面四元三角网的基本拓扑关系描述和计算［J］.测绘学报，2007，36（2）：176－180.）

［3］ KIESTER R，SAHR K.Planar and Spherical Hierarchical，Multi－resolution Cellular Automata［J］.Computers，Environment and Urban Systems，2008，32（3）：204－213.

［4］ HEIKES R，RANDALL D.Numerical Integration of the Shallow－water Equations on a Twisted Icosahedral Grid.Part I：Basic Design and Results of Tests［J］.Monthly Weather Review，1995，123（6）：1862－1880.

［5］ GIBSION L，LUCAS D.Spatial Data Processing Using Generalized Balanced Ternary［C］∥Proceedings of IEEE Computer Society Conference on Pattern Recognition and Image Processing.Las Vegas：IEEE，1982：566－571.

［6］ SAHR K.Discrete Global Grid Systems：A New Class of Geospatial Data Structure［D］.Oregon：The Graduate School of the University of Oregon，2005.

［7］ DONALD E K.The Art of Computer Programming：Seminumerical Algorithms［M］.3rd ed.Translated by SU Yunlin.Beijing：National Defence Industrial Press，2002.（DONALD E K.计算机程序设计艺术：半数值算法［M］.3版.苏运霖，译.北京：国防工业出版社，2002.）

［8］ VINCE A.Indexing the Aperture 3Hexagonal Discrete Global Grid［J］.Journal of Visual Communicatin and Image Representation，2006，17（6）：1227－1236.

［9］ ZHENG X Q.Efficient Fourier Transforms on Hexagonal Arrays［D］.Florida：University of Florida，2007.

［10］ MATTHEW G.Triangulation of a Hierarchical Hexagon Mesh［D］.Kingston：Queen＇s University，2009.

［11］ LIU Baihui，DU Li，YU Tao.A Method of Conversion between Decimal Number and Symmetrical Ternary Number［J］.Journal of Liaoning University，Natural Sciences Edition，1985（4）：29－35.（刘百惠，杜荔，于涛.十进制数与对称三进制数之间转换的一种算法［J］.辽宁大学学报：自然科学版，1985（4）：29－35.）