ISO与AGMA渐开线圆柱齿轮强度计算标准的比较

吴昌林 吕云霏

华中科技大学,武汉,430074

ISO与AGMA渐开线圆柱齿轮强度计算标准的比较

吴昌林 吕云霏

华中科技大学,武汉,430074

分析和比较了国际标准化组织(ISO)标准与美国齿轮制造者协会(AGM A)标准关于渐开线圆柱齿轮强度计算方法的差异,采用分类比较和实例对比的方法分析了两种标准的修正系数在含义和取值上的差异,以及齿轮的参数和修正系数对齿轮强度计算结果的影响。研究结果表明,两种标准的计算结果不存在其中一种比另一种更为保守的关系;AGMA标准的弯曲强度计算结果对齿轮的几何参数的变化更为敏感;参数和修正系数的取值不同是导致两种标准的计算结果产生差异的原因,其中疲劳极限、载荷、几何参数和寿命对接触强度计算结果的影响较大;试验齿轮的应力修正系数、载荷和几何参数对弯曲强度计算结果的影响较大。

ISO标准;AGMA标准;齿轮强度;比较

0 引言

关于渐开线圆柱齿轮的强度计算方法,国际标准化组织(ISO)和各主要工业国家都颁布了相应的标准,当前使用较多的是ISO标准与美国齿轮制造者协会(AGM A)标准[1]。我国现行的国家标准GB/T 3480-1997《渐开线圆柱齿轮承载能力计算方法》是等效采用的 ISO 6336-1～6336-3:1996标准。

国内外许多学者对ISO标准与AGMA标准进行过比较与分析,日本机械学会在1979年对几种主要的齿轮强度计算方法进行了较为详细的比较[2],但近年来,许多计算公式已经随着技术的发展进行了修改,其比较结果有待更新;周长江等[1]对ISO标准和AGMA标准的设计步骤、公式和系数含义进行了比较,并将分别采用两种标准计算的齿根应力与有限元分析的结果进行比较,认为两种标准的计算结果均偏大,即偏保守,且ISO标准的计算结果更为保守;Kawalec等[3]的研究结果则表明,按有限元方法计算得到的齿根应力大于AGM A标准的计算结果,小于ISO标准的计算结果;Cahala等[4]根据6组齿轮的许用应力计算结果,用统计学方法得出了一个简化的从ISO标准到AGMA标准的转换公式;Labath等[5]的研究表明,随着齿形、螺旋角、压力角等参数的变化,ISO标准和AGMA标准的强度计算结果呈现不同的变化趋势。以上研究对于齿轮设计与研究有着重要的参考价值,但均未明确分析导致两种标准的计算结果之间存在较大差异的原因。

本文分析和比较ISO标准与AGMA标准关于渐开线圆柱齿轮的强度计算方法的差异,着重比较两种标准的修正系数的含义和取值的差异,并分析齿轮的参数和修正系数对齿轮强度计算结果的影响。

1 计算公式比较

1.1 接触强度计算公式比较

1.1.1 强度条件

ISO 6336-2标准中,接触强度计算的基本公式为[6]

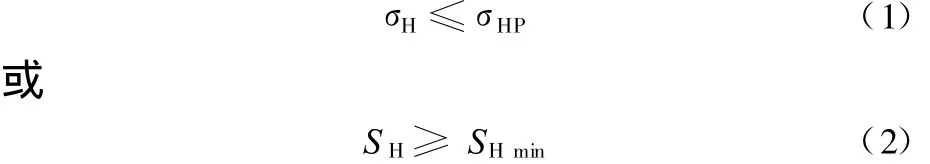
ANSI/AGMA 2101-D-2004标准中,接触强度计算的基本公式为[7]

需要注意的是,ISO标准中的σHP与AGM A标准中的σHP含义不同,前者为许用应力,后者为疲劳极限;ISO标准中的S H与AGMA标准中的S H含义也不同,前者为计算安全系数,后者为最小安全系数。

ANSI/AGMA 2101-D-2004标准中并未定义接触强度的计算安全系数,为了便于比较,参照ISO 6336-1标准[8],定义接触强度的计算安全系数为S H AGMA,则有强度计算公式:

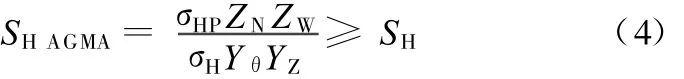
式(1)和式(3)的左右两端皆由计算得来,不易对两种标准的计算结果进行比较;式(2)和式(4)左端的计算安全系数由计算得来,右端的最小安全系数的取值由齿轮设计制造者与用户经过协商人为规定,对于同一对齿轮,最小安全系数确定后,比较分别用两种标准计算得到的计算安全系数的大小,即可对两种标准的强度计算结果进行比较,因此本文采用比较计算安全系数的方法来比较两种标准的强度计算结果。

1.1.2 计算安全系数公式比较

ISO 6336-2标准的接触强度计算安全系数公式为[6]

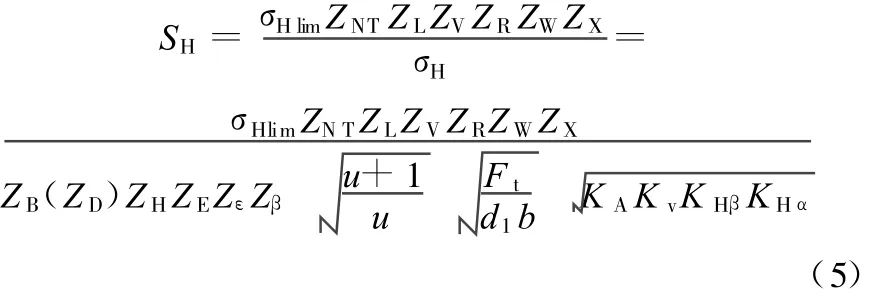
ANSI/AGMA 2101-D-2004标准的接触强度计算安全系数公式为

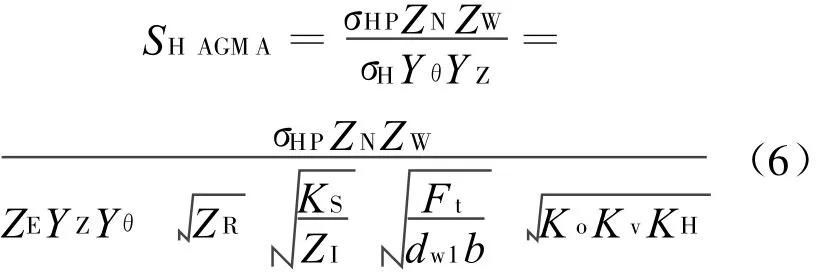
分析式(5)和式(6)可知,对于接触强度计算,ISO标准和AGMA标准的公式均是基于Hertz提出的两个弹性圆柱体接触面上的载荷分布公式,并引入若干修正系数,公式形式上具有一定的相似性,ISO标准引入的修正系数较多,考虑的影响因素较为全面,计算较为复杂,两种标准的修正系数含义的比较见2.1节。

1.2 弯曲强度计算公式比较

1.2.1 强度条件

ISO 6336-3标准中,弯曲强度计算的基本公式为[9]

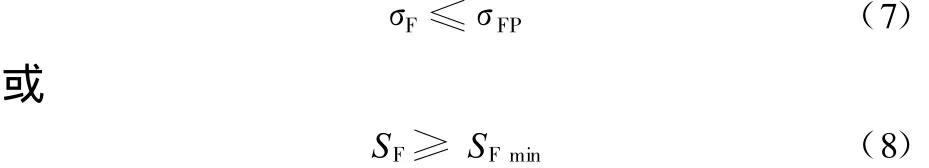
ANSI/AGMA 2101-D-2004标准中,弯曲强度计算的基本公式为[7]

需要注意的是,ISO标准中的σFP与AGMA标准中的σFP含义不同,前者为许用应力,后者为疲劳极限;ISO标准中的S F与AGMA标准中的S F含义也不同,前者为计算安全系数,后者为最小安全系数。

ANSI/AGMA 2101-D-2004标准中并未定义弯曲强度的计算安全系数,为了便于比较,参照ISO 6336-1标准[8],定义弯曲强度的计算安全系数为S F AGM A,则有强度计算公式:

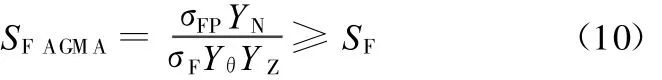
对于弯曲强度计算,本文同样采用比较计算安全系数的方法来比较两种标准的强度计算结果,原因见1.1.1节。

1.2.2 计算安全系数公式比较

ISO 6336-3标准的弯曲强度计算安全系数公式为[9]

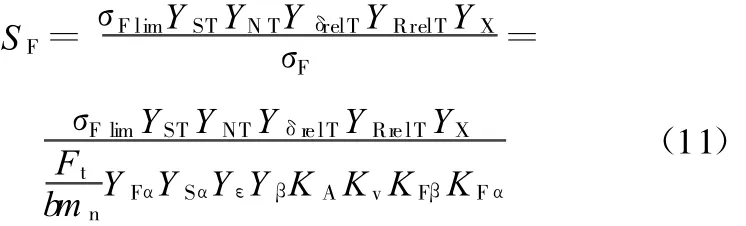
ANSI/AGMA 2101-D-2004标准的弯曲强度计算安全系数公式为

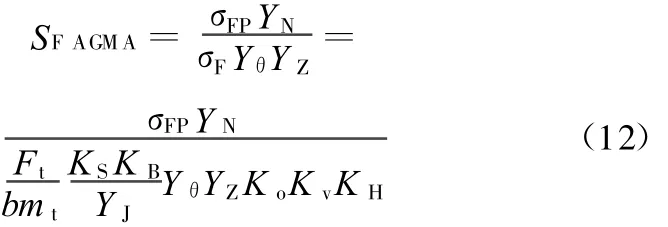
分析式(11)和式(12)可知,对于弯曲强度计算,ISO标准和AGM A标准的公式均是基于由抛物线梁理论推导出的Lew is公式,并引入若干修正系数,公式形式上具有一定的相似性,ISO标准引入的修正系数较多,考虑的影响因素较为全面,计算较为复杂,两种标准的修正系数含义的比较见2.2节。

ISO标准在计算公式中采用了法面模数m n,而AGMA标准的公式中采用的是端面模数m t,为便于比较,本文将AGMA公式中的m t转化为mn,即

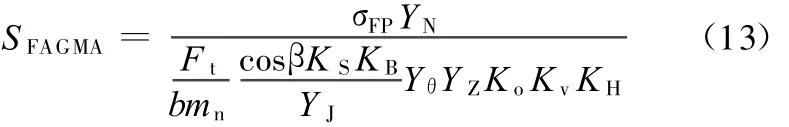
2 修正系数含义比较

2.1 接触强度计算的修正系数含义比较

由1.1.2节可知,ISO标准和AGMA标准的齿轮强度计算公式所引入的修正系数不完全相同。为了便于比较,本文根据修正系数所考虑的影响因素,将接触强度计算的修正系数分为六大类,将每一类的系数分别进行比较,比较结果如表1所示。

表1 接触强度计算的修正系数含义比较

分析表1可知,对于接触强度计算,ISO标准比AGMA标准考虑的影响因素更为全面,尤其是关于几何参数、材料特性和表面状况类影响因素,ISO标准引入的修正系数较多;AGMA标准虽然比ISO标准多考虑了温度和不同可靠性对齿轮强度的影响,但在一般的设计和使用条件下,Yθ、Y Z均取单位值,对结果没有影响。

2.2 弯曲强度计算的修正系数含义比较

由1.2.2节可知,ISO标准和AGMA标准齿轮强度计算公式所引入的修正系数不完全相同。为了便于比较,本文根据修正系数所考虑的影响因素,将弯曲强度计算的修正系数分为五大类,将每一类的系数分别进行比较,比较结果如表2所示。

表2 弯曲强度计算的修正系数含义比较

分析表2可知,对于弯曲强度计算,ISO标准比AGM A标准考虑的影响因素更为全面,尤其是关于几何参数、材料特性和表面状况类影响因素,ISO标准引入的修正系数较多;AGMA标准虽然比ISO标准多考虑了轮缘厚度、温度和不同可靠性对齿轮强度的影响,但在一般的设计和使用条件下,KB、Yθ、YZ均取单位值,对结果没有影响。

3 齿轮实例计算与分析

3.1 实例参数与强度计算结果

为了比较ISO和AGMA两种标准的修正系数和强度计算结果,对表3所示的两组齿轮进行计算,其强度计算结果如表4、表5所示。

由表4和表5可知,对于实例1中的软齿面齿轮,ISO标准的计算安全系数比AGMA标准的计算安全系数小,而对于实例2中的硬齿面齿轮则相反,因此不能得出其中一种标准比另一种标准的计算结果更为保守的结论;另外对于实例1,接触强度计算结果的差异较大,而对于实例2,弯曲强度计算结果的差异较大。

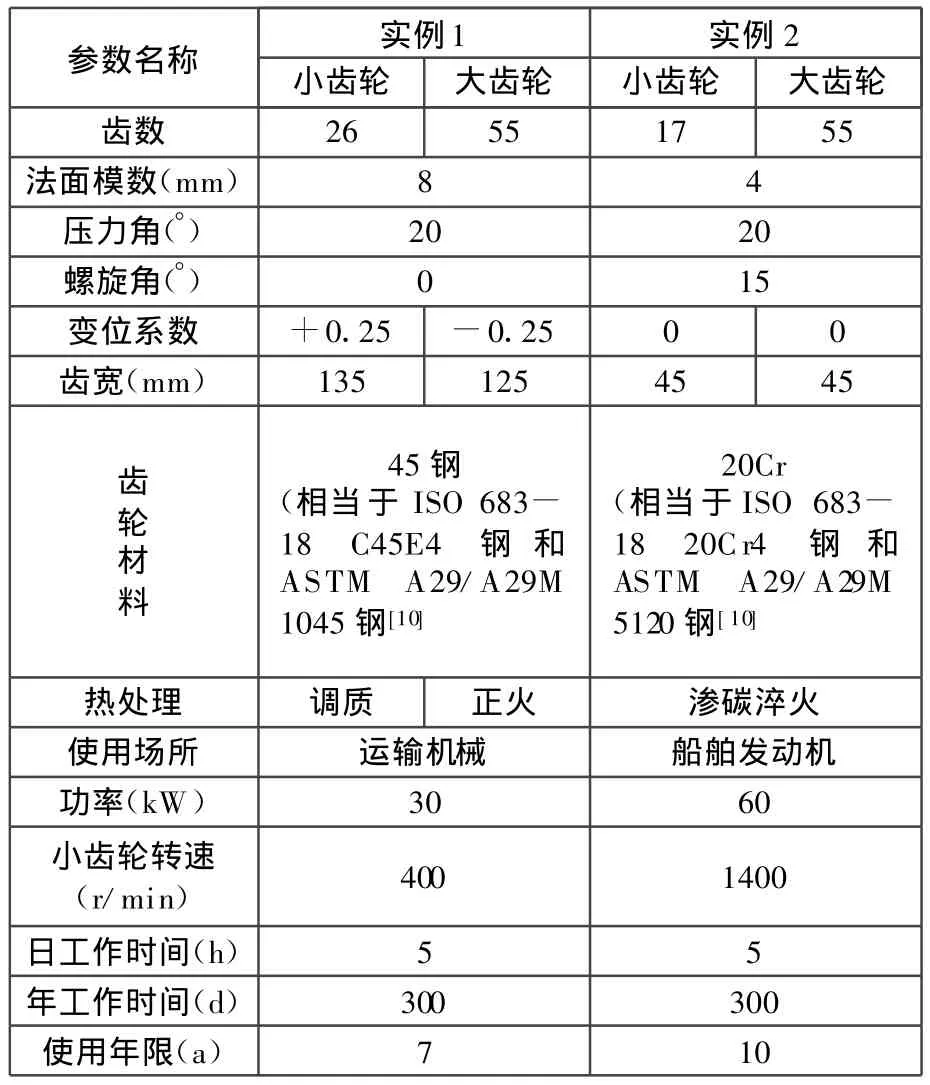
表3 实例齿轮参数

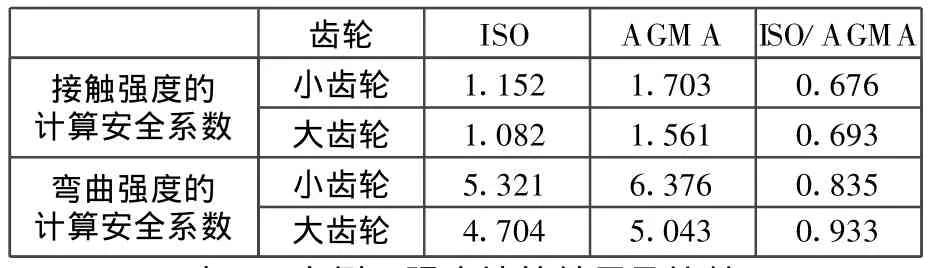
表4 实例1强度计算结果及比较

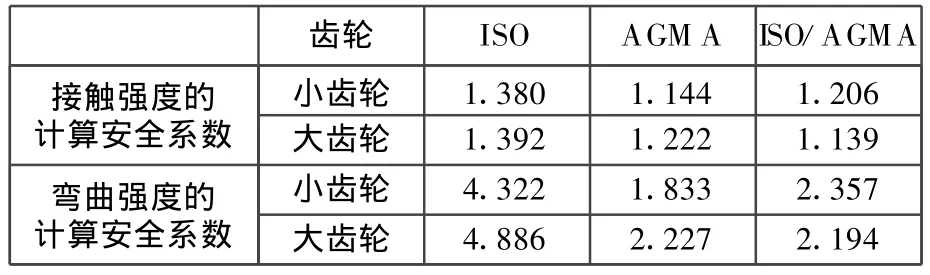
表5 实例2强度计算结果及比较

3.2 接触强度计算的系数比较与分析

由1.1.2节可知,接触强度的计算安全系数的公式可分解为齿轮材料的接触疲劳极限、工作齿宽、名义切向力等参数和各类修正系数的乘积。为了分析导致两种标准计算结果的差异的原因,本文将两种标准的修正系数按2.1节的方法进行分类,根据这些系数在式(5)和式(6)中所起的作用,分别比较各类修正系数对接触强度的计算安全系数的影响,同理将两种标准的计算公式中的参数进行分类比较。

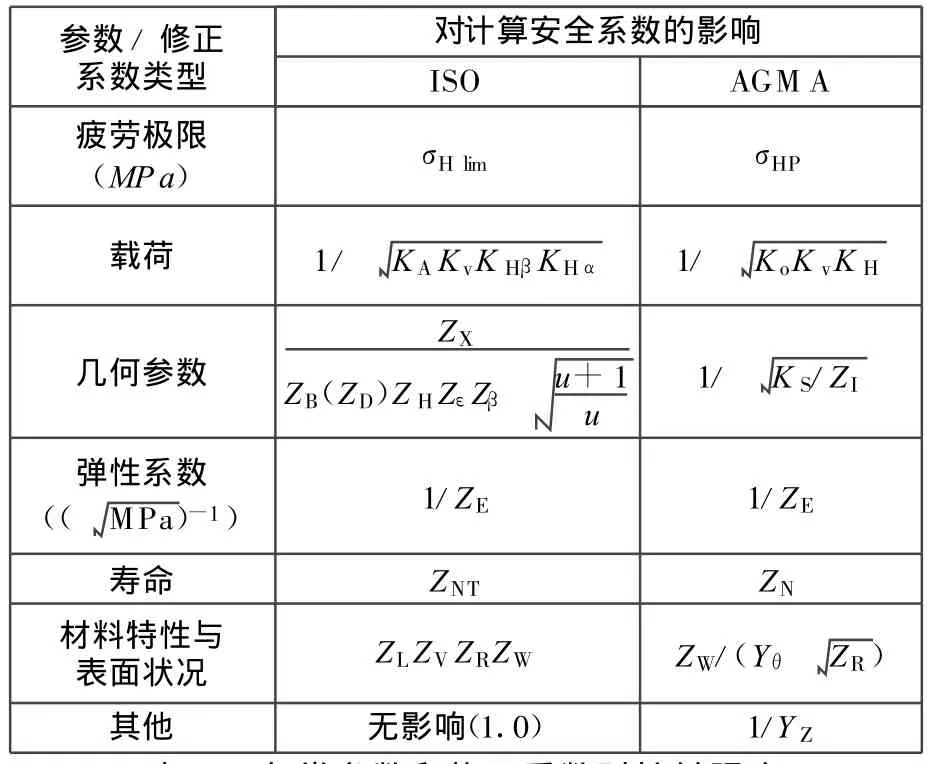
表6 各类参数和修正系数对接触强度计算安全系数的影响(代数式)

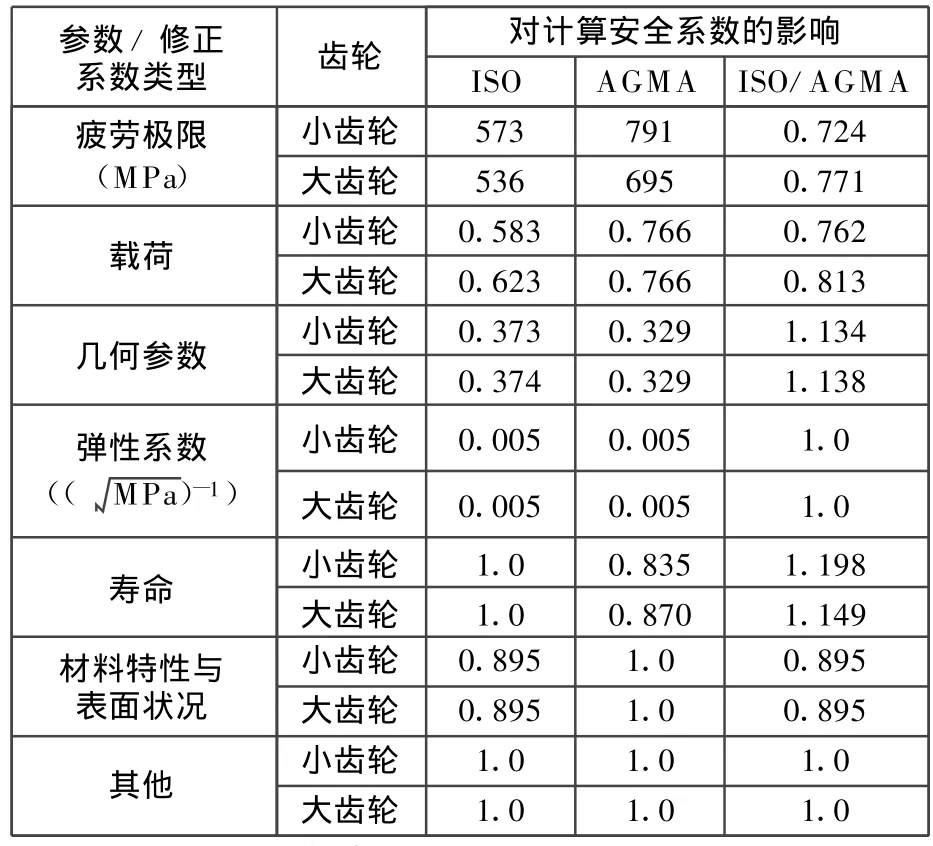
表7 各类参数和修正系数对接触强度计算安全系数的影响(实例1)

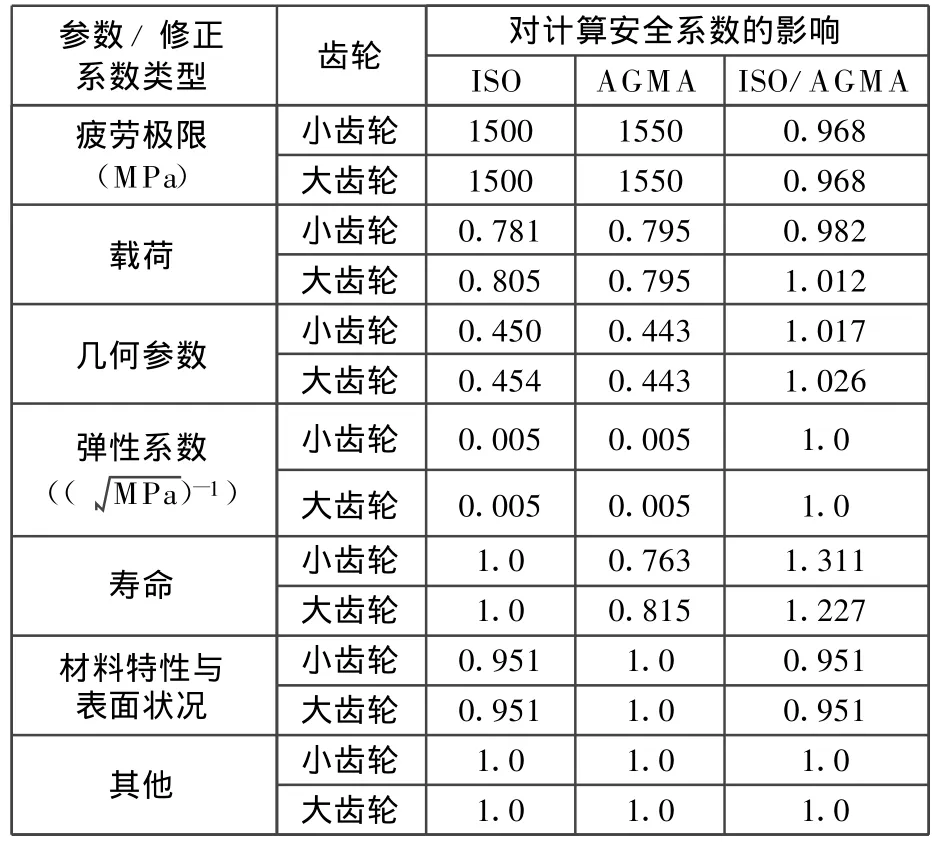
表8 各类参数和系数对接触强度计算安全系数的影响(实例2)

分析表7和表8可知,分别由ISO标准和AGMA标准计算得到的弹性系数相同,而疲劳极限以及载荷、几何参数、寿命、材料特性与表面状况类修正系数的不同是导致两种标准的计算结果产生差异的原因;对于实例1的软齿面齿轮,疲劳极限和载荷、几何参数、寿命类修正系数的差异较大;对于实例2的硬齿面齿轮,寿命类修正系数的差异较大。

3.3 弯曲强度计算的系数比较与分析

由1.2.2节可知,弯曲强度的计算安全系数的公式可分解为齿轮材料的弯曲疲劳极限、工作齿宽、名义切向力等参数和修正系数的乘积。为了分析导致两种标准计算结果的差异的原因,本文将两种标准的修正系数按2.2节的方法进行分类,根据这些系数在式(11)和式(13)中所起的作用,分别比较各类修正系数对弯曲强度的计算安全系数的影响,同理,将两种标准的计算公式中的参数进行分类比较。

由于式(11)中的 F t/(bm n)与式(13)中的F t/(bm n)相等,不需进行比较;为了便于比较,将ISO标准公式中的cosβ并入几何参数类的修正系数中。

具体的比较方法如表9所示,比较结果如表10和表11所示。

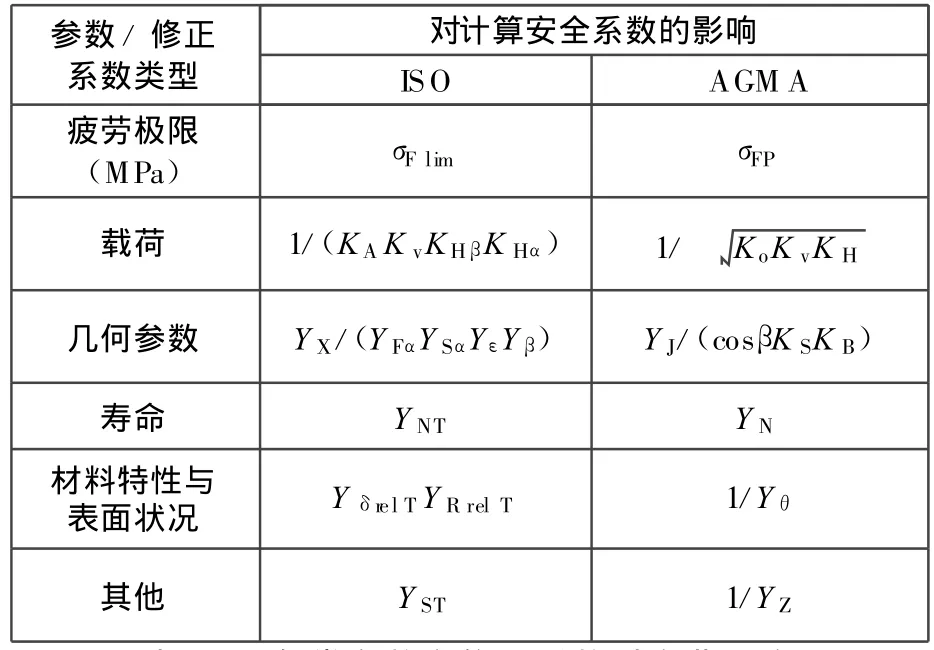
表9 各类参数和修正系数对弯曲强度计算安全系数的影响(代数式)

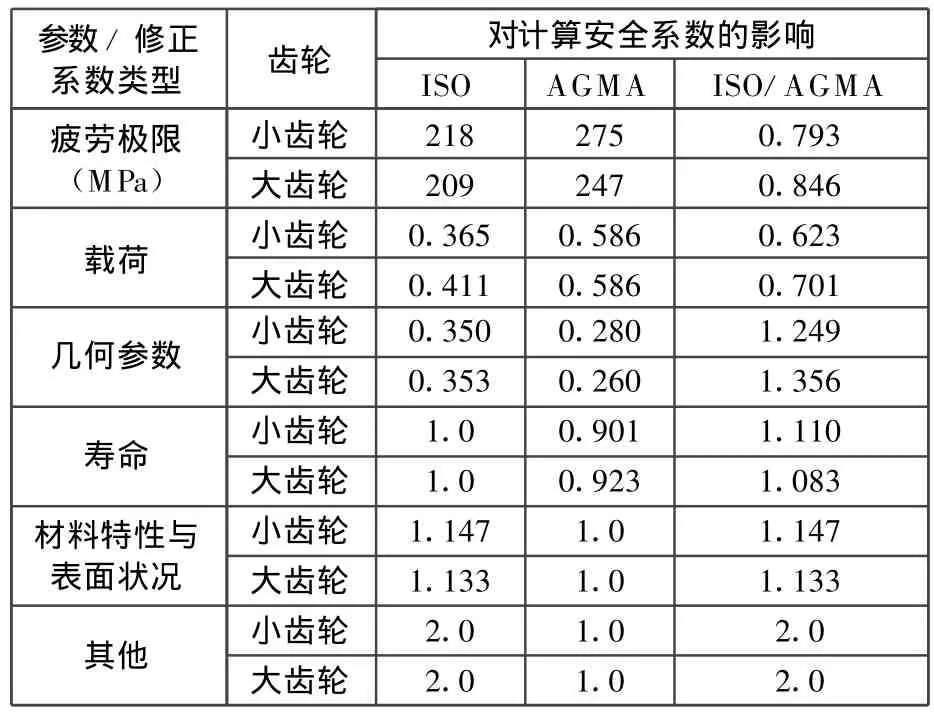
表10 各类参数和修正系数对弯曲强度计算安全系数的影响(实例1)

分析表10和表11可知,分别由ISO标准和AGM A标准计算得到的疲劳极限以及各类修正系数的不同,是导致两种标准的计算结果产生差异的原因。其中差异最大的是其他类修正系数,这是由于ISO标准引入了试验齿轮的应力修正系数

Y ST,当按ISO 6336-5标准选取σF lim值时,Y ST始终等于2.0。此外,对于实例1的软齿面齿轮,载荷和几何参数类修正系数的差异也较大,对于实例2的硬齿面齿轮,几何参数类修正系数的差异也较大。

3.4 对比齿轮组计算与分析

分析表4和表5可知,ISO标准和AGMA标准的计算结果中相差最大的是实例2的弯曲强度的计算安全系数,由3.3节可知,产生这一差异的主要原因是ISO标准引入的试验齿轮的应力修正系数Y ST和两种标准的几何参数类修正系数的差异。为了分析齿轮的几何参数对弯曲强度计算结果的影响,本文选取8组齿轮进行对比分析,该8组齿轮的参数如表12所示,其中大齿轮齿数值固定为55,其他未列在表12中的参数与实例2相同,计算结果如表13所示。

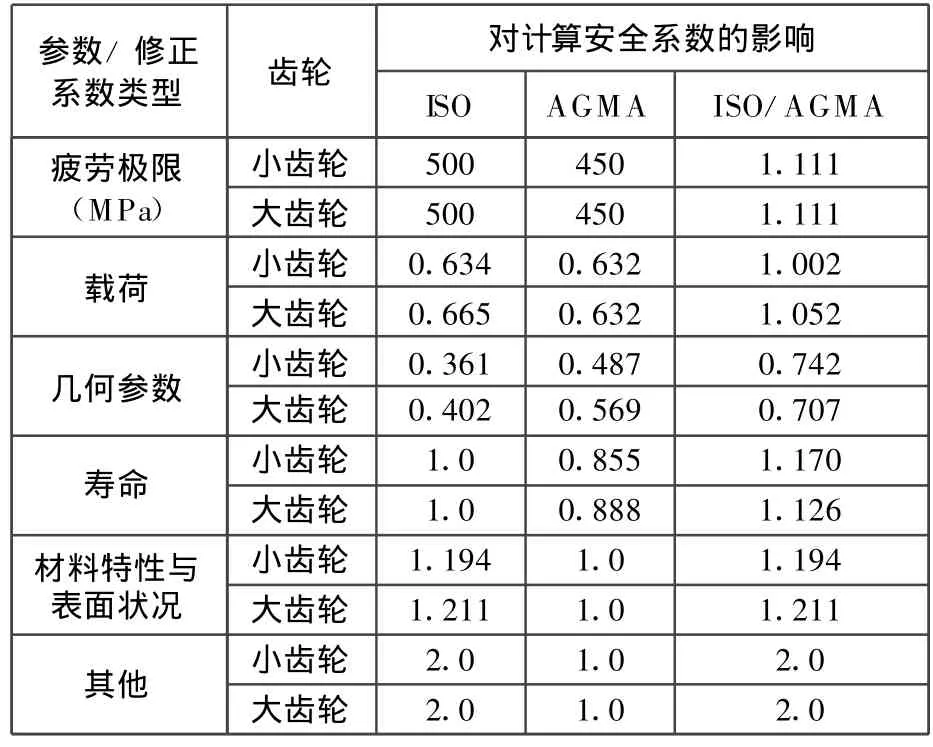
表11 各类参数和修正系数对弯曲强度计算安全系数的影响(实例2)

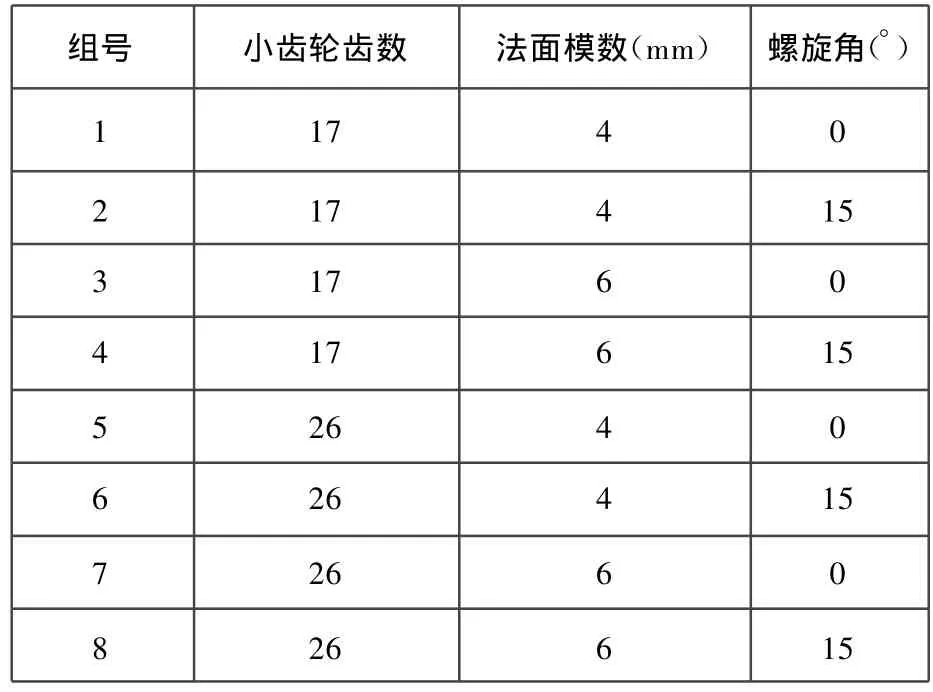
表12 对比齿轮组参数

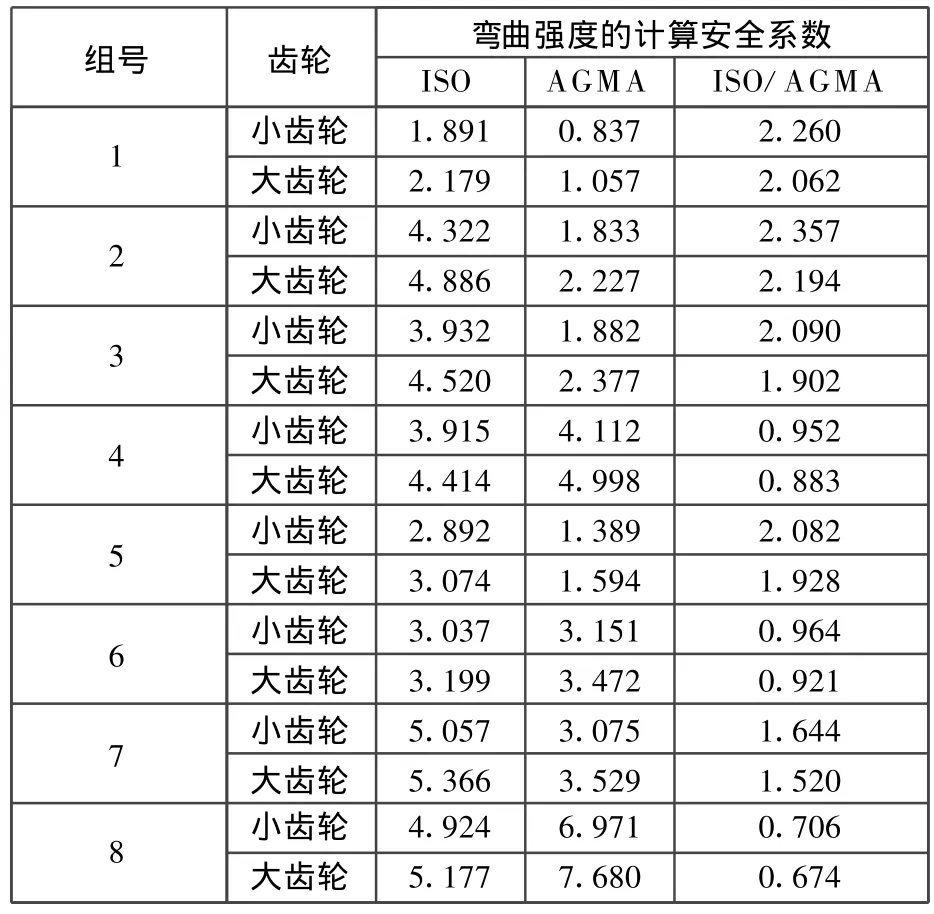
表13 对比齿轮组计算结果

对表13的计算结果随小齿轮齿数、法面模数和螺旋角的变化而发生变化的情况进行分析,分析结果如表14所示。

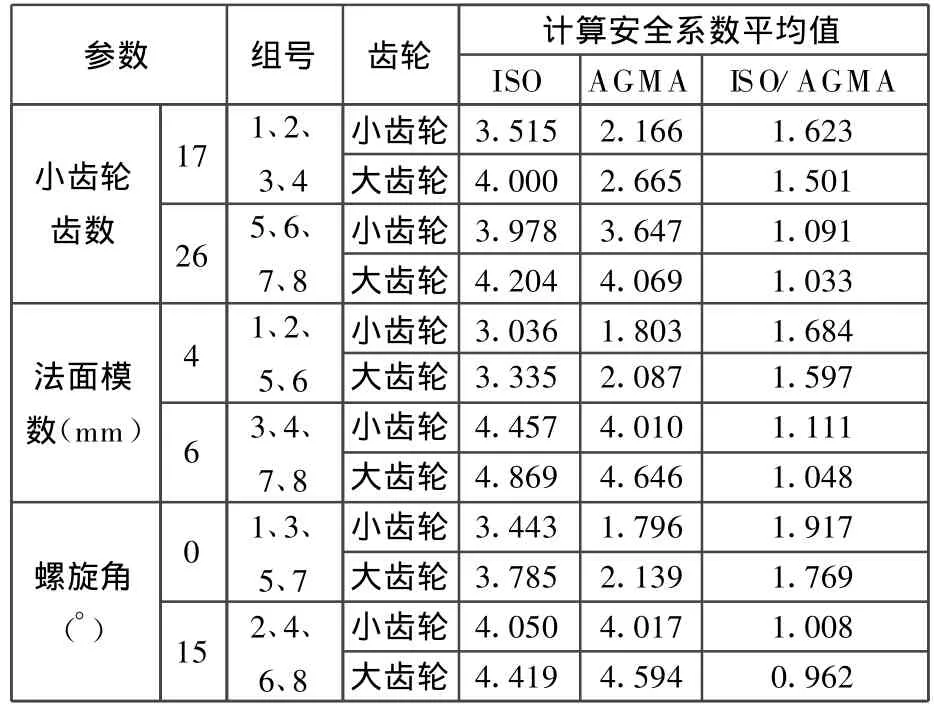
表14 对比齿轮组计算结果分析

由表14可知,随着小齿轮齿数、法面模数和螺旋角的增大,ISO标准和AGMA标准的弯曲强度的计算安全系数均增大,而ISO/AGMA的值减小,即AGMA标准的计算安全系数增长的幅度较大,对小齿轮齿数、法面模数和螺旋角的变化较为敏感。

3.5 两种标准的参数和修正系数取值不同的原因分析

由以上分析可知,ISO标准和AGMA标准的参数和修正系数的取值不同是导致两种标准的强度计算结果产生差异的原因,而两种标准的参数和修正系数之所以不同,主要是由于ISO标准与AGM A标准相比,前者更侧重于理论公式推导,并加入部分实验室试验数据,而后者则在理论的基础上引入了较多的来自工业实践的经验公式[4],两种标准的计算公式并不完全相同[6-9],具体表现如下:

(1)虽然两种标准的最基本的强度计算理论相同,但在一些具体的参数和修正系数的计算上,两种标准所采用的强度理论和计算方法并不完全相同,例如动载系数的计算、弯曲强度的危险截面的确定等[6-9]。

(2)两种标准的部分参数(包括修正系数计算公式中的参数)来源于齿轮试验,而在制定两种标准时所采用的试验设备、温度和润滑条件、钢材制造工艺、热处理工艺、齿轮加工工艺、试验齿轮的参数、对失效的判定标准等并不完全相同,因此由试验结果得到的参数的取值也会存在一定的差异。

4 结论

(1)从计算安全系数的比较结果来看,不能得出其中一种标准比另一种标准更为保守的结论,这与文献[1]的结论不完全一致,因文献[1]仅通过比较计算齿根应力来判断计算结果是否保,而未考虑许用应力对强度计算结果的影响。

(2)ISO标准比AGMA标准考虑的影响因素更为全面,引入的修正系数更多,计算更为复杂。参数和修正系数的取值不同是导致两种标准的计算结果产生差异的原因;对于接触强度计算,疲劳极限以及载荷、几何参数、寿命类修正系数对结果的影响较大;而对于弯曲强度计算,试验齿轮的应力修正系数Y ST以及载荷、几何参数类修正系数对结果的影响较大。

(3)用两种标准的弯曲强度计算公式计算的安全系数均随着小齿轮齿数(大齿轮齿数不变)、法面模数和螺旋角的增大而增大,其中AGMA标准的计算安全系数对以上几何参数的变化更为敏感。两种标准的弯曲强度计算结果随功率、转速、齿宽、变位系数等其他参数的变化而发生变化的规律以及接触强度计算结果的变化规律则有待进一步研究。

(4)两种标准对理论推导、试验数据和经验公式的偏重有所不同,在一些具体的参数和修正系数的计算上采用了不同的强度理论和计算方法,且两种标准所依据的试验结果的试验条件也不尽相同,这些因素导致了两种标准的参数和修正系数的取值存在一定的差异。

[1] 周长江,唐进元,刘艳萍,等.齿轮传动设计两种计算标准的比较研究[J].机械传动,2006,30(3):9-10,50.

[2] 日本机械学会.齿轮强度设计资料[M].李茹贞,赵清慧,译.北京:机械工业出版社,1984.

[3] Kaw alec A,Wik tor J,Ceg larek D.Comparative Analysis of Tooth-Root Strength Using ISO and AGMA Standards in Spur and He lical Gears with FEM-based Verification[J].Journal of Mechanical Design,2006,128:1141-1158.

[4] Cahala G.ISO 6336 vs AGMA 2001 Gear Rating Comparison for Industrial Gear App lications[C]//IEEE Industry Application Society's Cement Industry Committee.1999 IEEE Proceedings o f IAS/PCA Cement Industry Technical Conference.Piscataw ay,NJ:IEEE,1999:19-22.

[5] Labath O A,Richter D.Comparison of Rating T rends in AGMA Versus ISO[J].Gear Technology,2004,21(3):56-63.

[6] ISO.ISO 6336-2-1996 Calculation of Load Capacity of Spur and Helical Gears-Part2:Calcu lation o f Surface Durability(Pittings)[S].Geneva:ISO,1996.

[7] American Gear Manu facturers Association.ANSI/AGMA 2101-D-2004 Fundamental Rating Factors and Calcu lation Methods for Involute Spur and Helical Gear Teeth(Metric Edition)[S].A lexandria,VA:AGM A,2004.

[8] ISO.ISO 6336-1-1996 Calculation of Load Capacity of Spur and Helical Gears-Part 1:Basic Princip les,Introduction and General Influence Factors[S].Geneva:ISO,1996.

[9] ISO.ISO 6336-3-1996 Calculation of Load Capacity of Spur and Helical Gears-Part3:Calcu lation o f Tooth Bending Strength[S].Geneva:ISO,1996.

[10] 李维钺,李军.中外金属材料牌号速查手册[M].北京:机械工业出版社,2009.

Comparison between ISO and AGMA Gear Strength Rating Methods for Involute CylindricalGears

W u Changlin LǜYunfei
Huazhong University of Science&Technology,Wuhan,430074

Comparative analysis of involute cylindrical gear strength rating methods used by ISO standard and AGMA standard w as conducted.Gear parameters and derating factors w ere classified.Differences between themeaning and selection ofgear parameters and derating factors,aswellas their effectson gear rating results,w ere analyzed through calculations.The study indicates that neither of the two standards ismore conservative than the other one,and the bending strength rating results of AGMA standard are m ore sensitive to the change of gear geometry parameters.The study also indicates that different values of parameters and derating factors cause the differences in gear rating resu lts of the two standards.The allowab le stress number,load,geometry parameters and life have the most significanteffectson pitting resistance rating results;while the stress correction factor relevant to the test gears,load and geometry parameters have the most significant effect on bending strength rating results.

international standards organization(ISO)standard;American gear manu facturers association(AGM A)standard;gear strength;com parison

TH 12

1004—132X(2011)12—1418—06

2010—08—17

(编辑 何成根)

吴昌林,男,1951年生。华中科技大学机械科学与工程学院教授、博士研究生导师。主要研究方向为机械传动装置热系统分析的热网络方法、汽车齿轮动态和热态设计及三维修形、水工模型自动控制与检测、零部件表面自动抛光以及多作用容积式机器的开发等。发表论文100余篇。吕云霏,女,1986年生。华中科技大学机械科学与工程学院硕士研究生。