渐开线直齿圆柱齿轮的边缘效应与齿向修形初探
2011-01-29魏延刚
魏延刚
大连交通大学,大连,116028
渐开线直齿圆柱齿轮的边缘效应与齿向修形初探
魏延刚
大连交通大学,大连,116028
利用Pro/E参数化建模功能和齿轮啮合原理,实现了修形变位渐开线齿轮精确三维参数化建模,用有限元方法证明了渐开线直齿圆柱齿轮的边缘效应;应用啮合原理和接触力学基本概念,借鉴滚子轴承修形技术,结合齿轮传动的特点,对某齿轮传动进行了齿向修形设计,并用有限元法证实了齿向修形可有效避免边缘效应,大大降低齿轮传动中的最大应力。
渐开线齿轮;边缘效应;齿向修形;有限元分析
0 引言
很早以前就有人研究了接触问题中的边界应力集中问题,即所谓的边缘效应,如Johnson[1]在其“Contact Mechanics”(《接触力学》)一书中介绍了理想模型下刚性压头与半平面接触的边界应力集中问题。直母线滚子轴承的滚动体与滚道间的边缘效应问题在20世纪30年代就已经被滚动轴承界广泛注意,为了克服滚子类轴承的边缘效应,多年来人们做了大量有效的研究工作[2-7]。
渐开线直齿圆柱齿轮传动应用广泛,可以说经典的渐开线齿轮传动研究体系相当完善。然而,齿轮传动中的边缘效应迄今为止鲜有人进行专门研究。像渐开齿轮传动这样的渐开线曲面间的接触边缘效应问题难以用经典的力学方法来研究,本文用有限元方法对渐开线直齿圆柱齿轮的边缘效应问题进行了专门研究,研究了小轮单对齿啮合区内界点B、节点C及大轮单对齿啮合区内界点D这3个特征点啮合时的边界应力集中的情况,并针对边缘效应初步对所研究的齿轮传动进行了齿向修形设计,通过齿向修形大大降低了边界应力集中引起的最大接触应力。
1 渐开线齿轮啮合过程有限元分析和边缘效应
本文首先用Pro/E实现了变位渐开线齿轮精确三维参数化建模[8],再把模型导入有限元分析软件中,然后,对齿轮进行三维有限元接触分析,从而研究边缘效应问题。
1.1 渐开线外啮合直齿圆柱齿轮啮合过程的接触状态及载荷
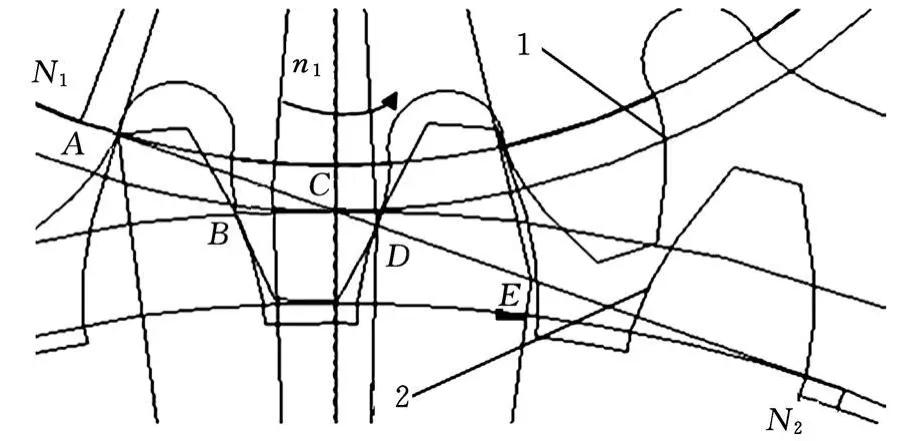
图1 外齿轮副的啮合情况
图1所示是一对重合度大于1的渐开线齿轮传动外齿轮副的啮合情况,N1、N2是两齿轮基圆的公切线上的两切点,线段 N1 N2便是这对齿轮的理论啮合线;A点是齿轮1齿根处与齿轮2齿顶圆上的啮合点,也是这对轮齿进入啮合的起始点;B点是小轮1单对齿啮合区内界点;C是节点;D点是大轮2单对齿啮合区内界点;E点是齿轮2齿根处与齿轮1齿顶圆上的啮合点,也是这对轮齿啮合的终点或说是脱离啮合的起始点;BD是单齿啮合区;AB、DE是双齿啮合区;AE是齿轮传动的实际啮合线。在齿轮传动啮合过程中轮齿上的载荷理论分布情况如图2所示,图中LMNOPQ表示载荷分布。
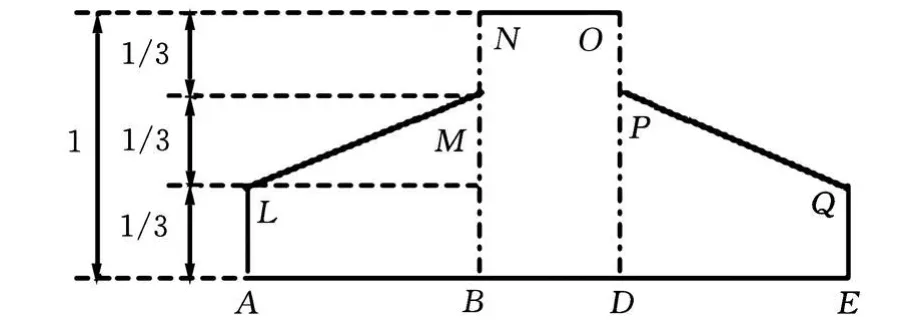
图2 轮齿上的载荷沿实际啮合线的分布示意图
1.2 齿轮啮合过程有限元分析模型
以某齿轮传动系统中的一对渐开线直齿圆柱齿轮为例,取主从动齿轮的弹性模量E1=E2=E=207GPa,泊松比μ1=μ2=μ=0.3,其齿轮参数为:主动轮齿数Z1=24,从动轮齿数Z2=50,模数m=2.8222mm,分度圆压力角20°,齿顶高系数1.35,齿顶间隙系数0.29,大齿轮宽度22mm,小齿轮宽度24mm,主动轮上的转矩T=208 340N◦mm。有限元模型的合理确定和网格划分,关系到有限元分析的计算精度和计算效率。利用齿轮啮合原理和接触力学理论,合理确定有限元分析模型,优化有限元网格的疏密,在保证计算精度的同时,提高计算效率。图3所示为该齿轮传动的有限元模型,其中,图3a为这对齿轮传动的整体模型,图3b为某瞬时啮合时的网格图,图 3c、图3d、图 3e分别为 B 、C、D 点啮合网格图,为节省计算时间和减少存储容量,有限元计算网格在齿宽方向仅取一半。

图3 齿轮传动有限元分析模型
1.3 齿轮啮合过程中的边缘效应
为节省篇幅,本文仅研究齿轮传动在3个典型啮合点(B点、C点和D点)啮合时的有限元计算结果,图4为齿轮传动在C点啮合时的等效应力云图,图5为齿轮传动在C点啮合时的接触应力云图;由图4和图5可以看出,最大接触应力和等效应力在齿向边界存在明显的应力集中。图6所示为齿轮传动在典型啮合点啮合时最大接触应力沿齿宽方向的变化曲线,坐标原点为齿宽中点。由图6可知,齿轮传动在B点、C点、D点啮合时,虽然应力数值有较大不同,但都有边界应力集中的现象。

图4 齿轮传动在C点啮合时的等效应力云图
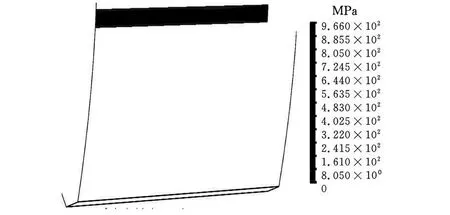
图5 齿轮传动在C点啮合时的接触应力云图
表1所示为齿轮传动在典型啮合点啮合时的接触应力和等效应力的边界应力集中情况,由表1可知,在B点啮合时的边界应力数值最大,在D点啮合时的应力数值次之,在C点啮合时的应力数值最小;边界最大接触应力分别是1441MPa、1079MPa和966MPa。应力集中情况则是在D点啮合时最大,在C点啮合时次之,在B点啮合时最小;接触应力理论应力集中系数分别为 1.58、1.33和1.27。

图6 齿轮传动在典型啮合点啮合时的最大接触应力沿齿宽方向的变化曲线

表1 齿轮传动在典型啮合点啮合时的接触应力和等效应力的边界应力集中情况
2 针对齿轮啮合过程中的边缘效应的修形设计与效果分析
2.1 齿向修形设计
针对上述边缘效应,应用齿轮啮合原理和接触力学基本概念,充分利用Pro/E的参数化建模功能,根据以往研究滚子轴承修形技术的经验[8-12],结合齿轮传动的特点和载荷大小,初步对所研究的齿轮传动进行了齿向修形设计,并实现了修形变位渐开线齿轮精确三维参数化建模[8]。齿向采用圆弧曲线修形,凸度量 C C=0.0025mm,齿轮有效宽度b=11mm,据此推导的齿向修形设计公式为


变位修形渐开线齿轮副的精确三维模型如图7所示。

图7 修形变位渐开线齿轮的三维精确模型
2.2 齿向修形效果分析
图8为齿轮传动在C点啮合时主动齿轮的等效应力云图。图9为齿轮传动在C点啮合时的接触应力云图。由图8、图9应力云图可见,在齿轮齿向端部边界处的应力集中已经不存在,最大应力不是出现在齿轮对齿向接触的边界处,而是出现在齿轮对齿宽中点处。
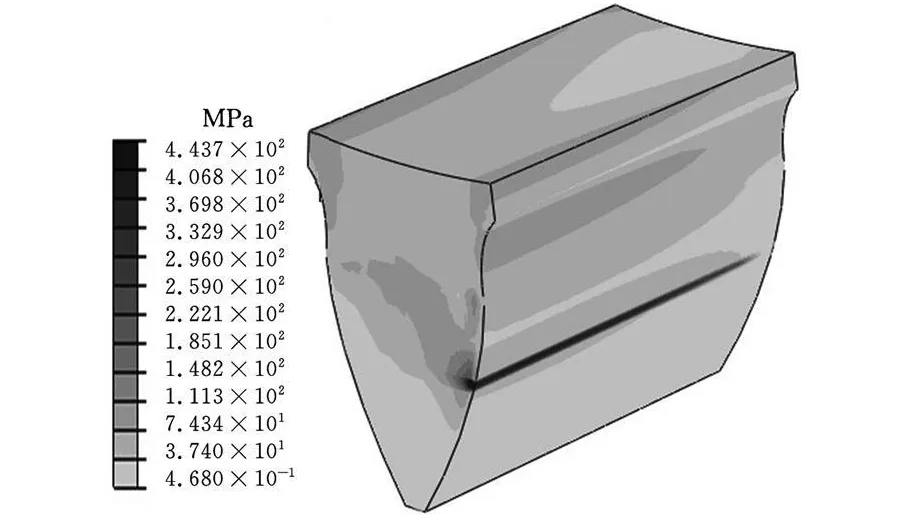
图8 齿轮传动在C点啮合时的等效应力云图

图9 齿轮传动在C点啮合时的接触应力云图
图10所示为齿轮传动修形前后在B点、C点和D点啮合时的最大接触应力沿齿向的分布情况,由图10可以清楚地看到,齿向修形改变了应力分布的规律,有效地避免了边缘效应,使修形后发生在齿宽中点的最大应力值小于修形前的边界应力值。另外,从图10还可以看出,修形效果在不同的啮合点啮合时效果不同。就本文研究的具体齿轮传动而言,修形效果在B点、C点啮合时相差不大,而在D点啮合时修形效果最佳。
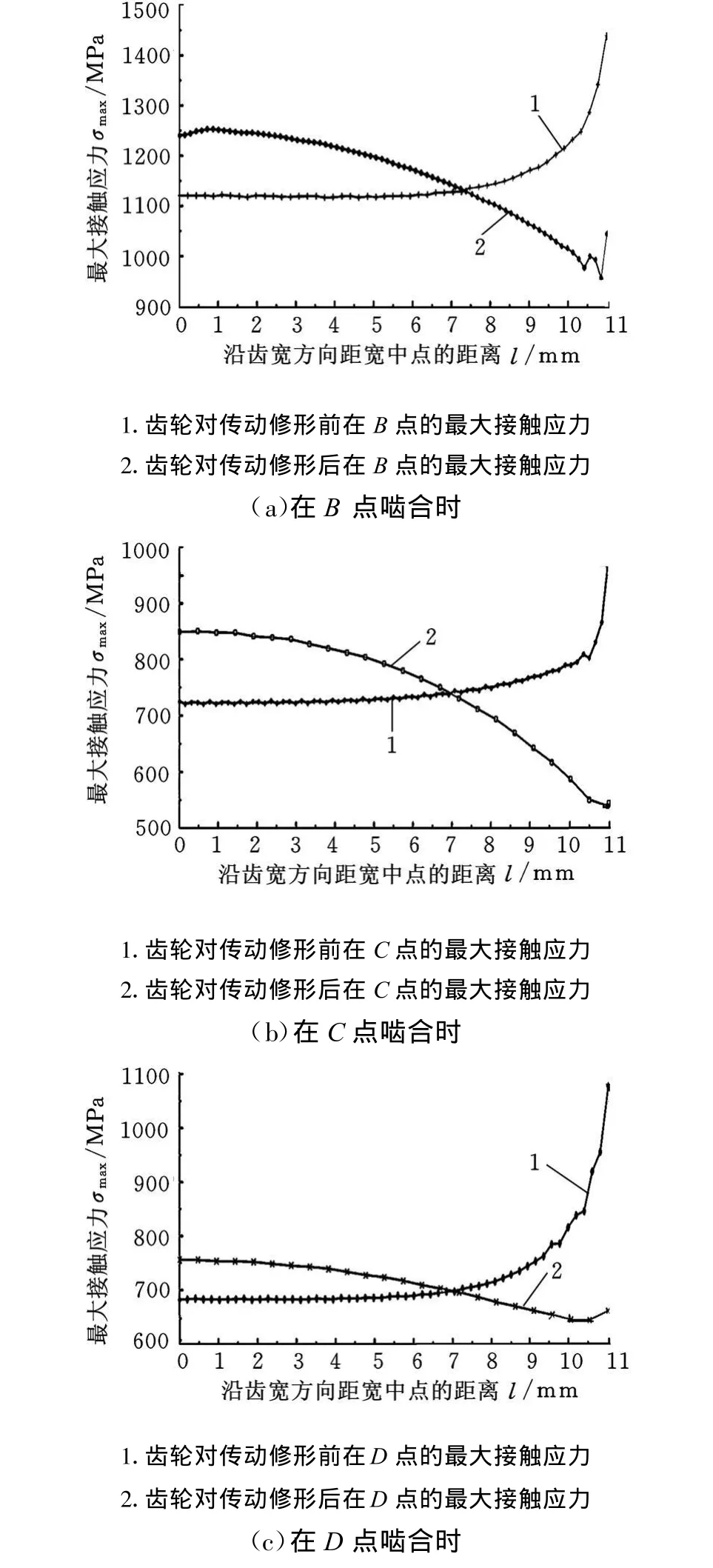
图10 修形前后齿轮传动最大接触应力沿齿向的变化规律比较
表2给出了修形后齿轮传动在典型啮合点啮合时边界和齿宽中点的最大应力。修形后与修形前相比,在B点啮合时齿宽中点最大接触应力由1136MPa增大到1253MPa,边界最大接触应力由1441MPa减小到1040MPa;在C点啮合时齿宽中点最大接触应力由724MPa增大到850M Pa,边界最大接触应力由966MPa减小到539MPa;在D点啮合时齿宽中点最大接触应力由683MPa增大到756MPa,边界最大接触应力由1079减小到644MPa。

表2 修形后齿轮传动在典型啮合点啮合时的边界和齿宽中点最大应力
表3所示为修形前后典型啮合点的最大接触应力和最大等效应力比较。

表3 修形前后典型啮合点的最大接触应力和最大等效应力比较
3 结论
(1)齿宽不相等的直齿圆柱齿轮不可避免地存在类似于滚子轴承的接触边缘效应。
(2)渐开线直齿圆柱齿轮边缘效应在不同啮合点啮合时引起的边界应力集中程度不同。
(3)齿向修形可以有效地避免边缘效应,改善应力齿向分布,从而大大减小最大应力。
(4)同一齿向修形设计对不同啮合点所产生的修形效果不同。
(5)本文的研究工作对于渐开线直齿圆柱齿轮传动的设计和制造有指导意义。
[1] Johnson K L.Contact Mechanics[M].Cambridge:Cambridge University Press,1985.
[2] Lundberg G,Palmgren A.Dynamic Capacity o f Rolling Bearings[J].Royal Swedish Academy o f Engineering Sciences,Stockholm,Sweden,1947,1(3):7-12.
[3] Kannel J W,Hartnett M J.Theoretical and Experimental Evaluation o f Edge Stresses under Severe Edge Loads[J].Trans.ASLE,1983,26(1):25-30.
[4] Chiu Y P,Hartnett M J.A Numerical Solution for the Contact Problem Invo lving Bodies with Cy lind rica l Surface Considering Cylinder Effect[J].Tans.ASM E,J.T ribology,1987,109:479-486.
[5] Reusner H.The Logarithm ic Ro ller Profile—the Key to Superior Performance of Cy lindrical and Taper Roller Bearings[J].Ball Bearing Journal,1987,230:2-10.
[6] H anson M T,Keer L M.Mechanics of Edge Effects on Friction less Contacts[J].Int.J.So lids Structures,1995,32(3/4):391-405.
[7] 陈晓阳,马家驹.对数型滚子凸度量设计中的几个问题[J].轴承,1994,11(11):2-4.
[8] Zhang Xiujuan,Wei Yangang,Liu Yankui,et al.Accurate 3-D Parameterized Modeling and Finite ElementContact Analysis of Involute X-gear Pairs with Tooth Modification[C]//2010 International Conference on Mechanic Automation and Control Engineering.Wuhan,2010:347-350.
[9] 魏延刚,马文.圆柱滚子轴承滚子凸度量的有限元分析[J].轴承,2004,4(4):1-4.
[10] 魏延刚,王忠敏,曲荣君.修形圆柱滚子轴承滚子凸度量设计[J].大连铁道学院学报,2004,9(3):23-25,27.
[11] 魏延刚,魏伟.圆柱滚子轴承滚动体新的修形曲线[J].机械设计与制造,2003,4(2):81-83.
[12] 魏延刚.圆柱滚子轴承滚动体修形技术的研究[J].润滑与密封,2003,5(2):16-18,22.
Research on Edge Effect and Longitudinal Modification of Involute Spur Cylind rical Gear Pairs
Wei Yangang
Dalian Jiaotong University,Dalian,Liaoning,116028
An accurate 3-D model of crow ning modification involute gear wasmade by combining parameterized m odeling function o f Pro/E w ith gear engagement theory.The edge effect in meshing process of involute spur cy lindricalgear pairwas validated by FED.Using gear engagem ent theory and contact mechanics theory,longitudinal m odification of gear pair was designed combining crowning technology of ro ller bearings w ith the characteristics of gear engagement.Then it is testified by FEA that longitudinal m odification can avoid the edge effect in the meshing process of involute spur cy lindricalgears,somaxim um stresses of gears can be reduced effectively.
invo lute gear;edge effect;longitudinalmodification;FEA
TH 132.46
1004—132X(2011)12—1413—05
2010—08—17
辽宁省自然科学基金资助项目(20082149);大连市产业技术创新基金资助项目(2008-1-215-JW-ZDCY)
(编辑 何成根)
魏延刚,男,1961年生。大连交通大学机械工程学院教授。研究方向为机械设计及理论、机械传动、机械产品数字化仿真与优化设计。获省级科学技术进步二等奖2项;获发明专利1项、实用新型专利3项。发表论文70余篇。
