考虑控制电路失谐的叶盘结构振动控制研究
2011-01-29王艾伦
王艾伦 李 林
中南大学现代复杂设备设计与极端制造教育部重点实验室,长沙,410083
考虑控制电路失谐的叶盘结构振动控制研究
王艾伦 李 林
中南大学现代复杂设备设计与极端制造教育部重点实验室,长沙,410083
以适用于多能域系统建模的功率键合图为工具,建立了叶盘结构与压电回路耦合动力学模型,研究了电路参数失谐对叶盘结构振动特性的影响规律,并进行了验证。研究结果表明:控制电路失谐会使叶盘结构的动力学特性受到影响,且其影响大小与失谐支路离失谐叶片的距离有关,距离越远影响越小;在同一支路的各个参数中,电阻失谐对叶盘结构的最大振幅影响最大,电容失谐不影响叶盘最大振幅。此外,研究发现:控制电路失谐不一定会加剧叶盘结构振动局部化,在某些电路失谐模式下,叶盘结构振动局部化程度反而减小,说明谐调压电循环周期电路对失谐叶盘结构振动的控制效果并非最佳,而设计适当失谐的压电控制电路反而能得到更好的振动控制效果。
叶盘结构;振动主动控制;压电回路;失谐
0 引言
叶盘结构是典型的循环周期结构,由于加工误差及不均匀磨损等原因,叶片的外形、质量和刚度等结构参数不可避免地存在着差异,这种差异称为失谐。失谐会导致叶盘结构的模态振型沿周向分布不均,某些叶片模态将远大于其他叶片模态,即振动局部化[1],这将造成少数叶片在共振区内的振动应力过大,从而大大增加了叶盘结构高周循环疲劳破坏的风险[2]。
目前,失谐叶盘结构的相关研究集中在对振动局部化成因的探索,以及对局部化响应的理论计算方面,对失谐叶盘结构振动局部化的控制方法的研究极少,且已有的控制方法绝大多数是利用压电材料的力电耦合特性来实现对失谐叶盘结构振动局部化控制的。文献[3-4]利用压电材料的压电特性,提出一种降低失谐周期结构振动局部化的新方法。在各个叶片的根部嵌入压电片,用电回路将各压电片连接,他们发现此时叶片间的耦合强度增大,失谐叶盘结构的振动局部化程度降低。文献[5-7]在此基础上对电路形式进行改进,设计了一种与叶盘结构相耦合的压电循环周期电路,并验证了这一方法的有效性。这些研究都基于电路系统谐调这一前提,但实际上在这种控制方法中,电路系统是由分支电路构成的循环周期结构。同样由于电子元件制造等原因,电路系统也必然存在失谐。研究电路失谐对叶盘结构振动特性的影响规律对压电回路的设计具有指导意义。
此外,叶盘结构和压电回路构成了多能域耦合系统,由于机械系统和电路系统有各自的一套理论、概念、符号和量纲,在采用一般的动力学建模方法建模时,建立的数学模型不能够清晰地表达这种多能域耦合关系。键合图方法具有多能域间符号、概念高度统一性及高度规范性等优点[8],用键合图方法建立叶盘结构与压电回路耦合系统的动力学模型,能够直观、清晰地反映它们之间的耦合关系。
本文以功率键合图方法为工具,研究基于压电阻尼技术的失谐叶盘结构振动控制方法中控制电路失谐对叶盘结构动力学特性的影响规律。分析不同分支电路各个电参数的失谐量对控制效果的影响,探讨控制电路失谐形式对叶盘结构振动特性的影响规律,为叶盘结构振动控制设计提供理论指导。
1 系统模型及动力学方程
1.1 系统模型
图1所示为叶盘结构和压电回路系统的物理模型。叶盘结构由 N个沿周向分布的完全相同的叶片构成。在各叶片根部嵌入压电片,压电片间通过循环周期电路连接。分支电路由电感L、电阻R组成,各分支电路之间通过电容C a耦合。为方便分析,分别对叶片及分支电路进行了编号。

图1 叶盘结构-压电回路系统物理模型
为建立叶盘结构的键合图模型,必须先将其物理模型离散化,才能得到图2a所示的集中参数模型。图2中,m和K分别为叶片的质量和刚度,K s和C分别为相邻子结构间的刚度和阻尼,F为外部激励。由集中参数模型可以方便地建立图2b所示的叶盘结构键合图模型。
在本控制系统中,压电片利用压电材料的正负压电效应,使系统的一部分能量在电能与机械能间转换,故可将压电片视作转换器及电容的组合,其键合图模型可写为。于是可以得到图3所示的压电回路的键合图模型。

图2 叶盘结构集中参数模型和键合图模型

图3 压电回路键合图模型
合并图2和图3可以得到图4所示的叶盘结构-压电回路系统耦合键合图模型,图中内外环分别对应叶盘结构和压电回路。对比图1和图4可以看出,键合图模型与物理模型之间具有完全确定的拓扑对应关系。

图4 叶盘结构-压电回路系统键合图模型
1.2 动力学方程
根据图4所示的键合图模型可以得到叶盘结构-电回路系统的动力学状态方程:

X为状态矩阵,Xj(j=1,2,…,N)为6维向量,包括第j个叶片的1个动量变量和2个变位变量,以及第j条分支电路的1个动量变量和2个变位变量。各叶片的振幅可以根据叶片的动量计算得到。

式中,Sej为叶片所受的气流作用力;j为叶片序号;F0为激振力幅值;ω为激励频率;E为激励阶次。
2 谐调电路参数值的选取
设图1的循环周期结构为12叶片叶盘结构,考虑叶片刚度随机失谐,其他结构参数不失谐。记:


式中,Ra为分支电路间量纲一耦合强度;ε为叶盘结构与电路系统间的耦合强度;ζr为电路模态阻尼比。
例如,对“氨基酸脱水缩合”的概念,笔记可促进学生建立与“单糖形成二糖,甘油、脂肪酸形成脂肪,ATP的合成与水解,DNA的合成与水解”等知识的联系,其实质是学生原有的知识与有机化学中的“酯化反应”相联系,从而实现学生跨学科知识的融合,有利于学生更好地运用知识解释生活中的生物学现象。
为了便于分析,将控制效果量化表示,定义控制性能因子:
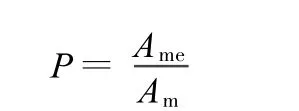
式中,Am、Ame分别为控制前后失谐叶盘结构叶片最大振幅,从定义式可以看出,性能因子越小,控制效果越好。
图5、图6所示为电路频率调谐比 δ为 0.90、0.95、1.00、1.05、1.10时模态阻尼比和耦合电容的取值对性能因子的影响。由图5、图6可知,电路频率调谐比δ=1时,性能因子最小,这是因为电路的固有频率等于叶片的固有频率时,系统能量在机械能与电能之间最大程度地转换,机械子结构和电路子结构间耦合度最大;当δ=1,电路模态阻尼比ζr取值在0.04~0.08之间,耦合电容R a取值在0.1~0.2之间时,性能因子最小,控制效果最好。故将谐调电路的各参数取值为δ=1,ζr=0.055,R a=0.16。

图5 模态阻尼比对控制性能的影响

图6 耦合电容对控制性能的影响
3 电路失谐对叶盘结构最大振幅的影响
叶盘最大振幅反映了失谐叶盘结构的振动局部化程度,且最大振幅直接影响结构的工作寿命,本节研究控制电路失谐对叶盘结构最大振幅的影响。
假设叶盘结构第3个叶片刚度失谐,失谐量为2%,其余叶片谐调。由于电子元件的制造误差较大,考虑电参数最大失谐量为5%。图7所示为不同分支电路参数失谐对叶盘最大振幅的影响,从图中可知,支路 Ⅲ参数失谐对叶盘最大振幅影响最大,支路 Ⅴ失谐影响最小。说明与失谐叶片(叶片3)耦合的支路的失谐对叶盘最大振幅影响最大,离失谐叶片越远的分支电路的失谐对叶盘最大振幅的影响越小。

图7 电路参数失谐对叶盘结构最大振幅的影响
从图7a可以看出,在支路Ⅲ各参数中,叶盘最大振幅对电阻失谐最为敏感,电阻失谐量为5%时,最大振幅有最大值,此时相比电路谐调时增大近5%,振动控制效果极大减弱;电容失谐对叶盘最大振幅的影响曲线为一条水平直线,说明电容失谐不会影响叶盘最大振幅。
此外,从图7可知:当支路Ⅲ的电阻失谐量为-4.1%~0,电感失谐量为-6%~0时,叶盘结构的最大振幅相比电路谐调时明显减小,支路Ⅳ在电阻失谐量为0~2%和电感失谐量为-2%~0时亦有类似规律。说明谐调控制电路对失谐叶盘结构的控制效果并非最佳,设计失谐量适当的失谐电路能起到更好的振动控制效果。
4 电路不同失谐模式下叶盘最大振幅响应
4.1 理论计算分析

假设叶片3刚度失谐,其失谐量为2%。从前述可知,相比支路 Ⅲ参数失谐,支路 Ⅳ、Ⅴ的失谐对叶片振幅影响很小,所以只考虑支路 Ⅲ失谐下叶片振动响应。图8所示为叶盘最大振幅频率响应。从图8可以看出,相比电路谐调,电路失谐形式为表1模式一时叶片最大振幅极大增大,当量纲一激励频率为1.035时,叶片最大振幅超过50%;而电路失谐形式为表1模式二时,叶片最大振幅减小,说明此时能量在局部叶片的聚集程度降低,叶盘结构振动局部化程度减弱,这与叶盘结构自身结构参数失谐对振动局部化的影响规律不同。从这一结论可知,相比控制电路谐调,设计适当的失谐控制电路能够更有效地降低失谐叶盘结构的振动局部化程度。

图8 叶盘最大振幅频率响应

表1 电路失谐模式
4.2 试验对比分析
本试验以12叶片叶盘结构及其控制电路为试验对象,叶盘结构和压电片的几何参数及材料属性分别如表2、表3所示。

表2 叶盘结构几何参数 mm
叶片可以看作悬臂梁,根据悬臂梁弯曲振动固有频率计算公式,可得叶片振动的第一阶固有频率:


表3 压电片几何参数及材料属性
试取模态阻尼比ζr=0.055,R a=0.16,由δ=1可计算得各电路元件值:R=11.8Ω,Ca=128.9nF,L=75.7m H。查电元件标准,选择谐调电路各参数为 R=11.8Ω,C a=120nF,L=68mH。电路失谐形式分别为失谐模式一、二时,支路 Ⅲ各元件的参数值如表4所示。

表4 失谐支路元件参数值
试验采用压电激振法[9],利用LMS振动测试仪对叶片振幅信号进行采集,在同一激励频率下取5次测量平均值,测得的不同失谐模式下的叶片最大振幅响应如图9所示。

图9 叶盘最大振幅响应实测值
从图9可知,控制电路失谐会对叶盘结构的动力学特性产生影响,但其影响并不是具备规律性,控制电路的失谐模式不同,叶盘最大振幅响应受到的影响亦不同。当电路失谐量为ΔR=5.08%,ΔL=4.85%,ΔCa=0 时,叶盘最大振幅相比电路谐调时增大;当电路失谐量为ΔR=-2.5%,ΔL=-2.94%,ΔC a=0 时,叶盘最大振幅则减小,振动局部化程度减弱,说明相比电路谐调时,失谐模式二下的压电回路有更好的控制效果,这与理论分析结果一致。
5 结论
(1)叶盘结构的最大振幅对与失谐叶片耦合的分支电路的失谐最为敏感,失谐分支电路离失谐叶片越远,叶盘结构最大振幅受影响越小。
(2)在同一支路的各个参数中,电阻的失谐对叶盘结构最大振幅影响最大,电容失谐则不会影响叶盘最大振幅。
(3)与叶盘结构自身结构参数失谐对振动局部化的影响规律不同,电路参数失谐不一定会加剧叶盘结构的振动局部化,在某些电路失谐模式下,叶盘结构振动局部化程度反而减小,说明相比谐调压电周期电路,失谐模式适当的压电控制电路对叶盘结构振动的控制效果更佳。
[1] Hodges C H,Confinement of Vibration by Structural Irregu larity[J].Journal of Sound and Vibration.1982,82(3):411-424.
[2] Kenyon J A,Griffin J H,Feiner D M.Maximum Bladed Disk Forced Response from Distortion o f a Structural Mode[J].ASME Journal o f Turbomachinery,2003,425(2):352-363.
[3] Cox A M,Agnes G S.A Statistical Analysis o f Space Structure Mode Localization[C]//Proceedings o f the 1999 IAA/ASM E/ASCE/AHS/ASC Structures,Structural Dynam ics,and Materials Conference and Exhibition,St.Louis:AIAA,1999:3123-3133.
[4] Agnes G S.Piezoelectric Coup ling of Bladed-disk Assemblies[J].Proceedings of SPIE,1999,3672:94-103.
[5] Tang J,W ang K W.Vibration Controlof Rotationally Periodic Structures Using Passive Piezoelectric Shunt Netw orks and A ctive Com pensation[J].Journalof Vibration and Acousticst,1999,121(3):379-390.
[6] Zhang J,W ang K W.Electromechanical Tailoring o f Piezoelectric Netw orks for V ibration Delocalization and Suppression o f Nearly Periodic Structures[C]//Proceedings of the 13th International Conference on Adaptive Structures and Technologies.Berlin:ICAST,2002:199-212.
[7] Yu H,W ang K W.Vibration Suppression of M istuned Coup led-b lade-disk System s Using Piezoelectric Circuitry Network[J].Journal of Vibration and Acousticst,2009,131(2):021008
[8] 王艾伦,钟掘.模态分析的一种新方法——键合图法[J].振动工程学报,2003,16(4):463-467.
[9] H ohl A,Neubauer M.Modelling of Shunted Piezoceram ic A ctuators with Substructure Techniques and Application to a Bladed Disk Model[C]//2009 IEEE/ASME Internationa l Conference on Advanced Intelligent Mechatronics.Singapore:ASME,2009:1088-1093.
Study on Vibration Control of Bladed Disk Structure Considering CircuitM istuning
W ang Ailun Li Lin
Key Laboratory o f Modern Comp lex Equipment Design and Ex treme Manufacturing(Central South University),Changsha,410083
A dynamicmodelofbladed disk structurew ith coup led piezoelectric network wasestablished based on bond graph,which is an effective tool for modeling of system w ith multi-energy dom ains.The effects of circuit mistuning on vibration characteristics o f b laded disk w ere investigated.Then an experimentwas design to validate the conclusion.The resu lts show that circuitmistuning will influence the dynamic characteristics of bladed disk,the effect is related to the distance between the blade and mistuned shunt circuit,the greater the distance the sm aller the impact.A nd resistancemistuningmakes the greatest effect on blade maximum amp litude,while capacitancemistuning has no effect.Additionally,the study indicates that circuitm istune doesnotalways aggravate vibration localization in b laded disk,w hich m ay be decreased under certain circuit mistune mode.It indicates that com pared to tuned piezoelectric netw ork,an app rop riatem istuned network can supp ress b laded disk vibration better.
bladed disk structure;active vibration control;piezoelectric network;m istuning
TK 261;TH 113.1;O328
1004—132X(2011)12—1387—06
2010—08—09
国家重点基础研究发展计划(973计划)资助项目(2007CB707706)
(编辑 何成根)
王艾伦,男,1959年生。中南大学机电工程学院副院长、教授、博士研究生导师。主要研究方向为机械动力学和高等机构学。参编专著2部。发表论文60余篇。李 林,男,1985年生。中南大学机电工程学院硕士研究生。
