RDX 基含铝炸药的热爆发活化能及动力学补偿效应
2011-01-28郑亚峰刘子如许西宁邵颖惠衡淑云
常 海,郑亚峰,刘子如,许西宁,邵颖惠,衡淑云
(西安近代化学研究所,陕西 西安710065)
引 言
一般而言,含能材料热爆发活化能Eb的物理意义为:有足够量的含能材料活化分子越过了某个“能垒”发生了热爆发反应,该“能垒”就是“活化能”[1-2]。在一定的条件下,热爆发活化能Eb越高,越不容易发生热爆发,安定性就越好。因此,研究含能材料组分含量对热爆发活化能Eb的影响对其在生产、贮存和运输等过程中的安全性有重要的意义。
许多材料的热分解反应动力学参数存在“动力学补偿效应”,即Arrhenius方程中指前因子的对数lnA与活化能Ea有线性关系[1-7]。Brill等人[7]认为这种关系是由于绝对速度理论(或称过渡状态理论)所确定的活化自由能△G*为恒定值并存在线性关系:△G*=Ea-T△S*。当Ea增大时,与lnA密切相关的活化熵△S*也增加给以补偿,补偿效应意味着所研究的过程有同一反应或速度决定步骤,若Ea-lnA数据组不在补偿回归线上或不在该线附近,则表明有不同的分解反应过程或数据不正确。因此,动力学补偿效应提供了一个在大量Arrhenius参数中选择合理描述热分解宏观速率的方法。一般来说,动力学补偿效应都是对同一种物质的热分解反应,研究发现该RDX 基含铝炸药体系的热爆发动力学参数lnA和Eb也存在动力学补偿效应。本文根据文献[8]中的数据,研究热爆发动力学参数的动力学补偿效应。
1 实 验
1.1 材料及仪器
RDX,Ⅱ类,甘肃银光化学工业集团有限公司;铝粉,粒径13μm,中国铝业股份有限公司西北铝加工分公司。
爆发点测试仪,西安近代化学研究所,药量30mg。
1.2 样品的制备
采用直接法制备RDX 基含铝炸药,即将黏结剂用乙酸乙酯加热到50℃溶解,加入RDX、铝粉和黏结剂(具体配方见表1),然后边搅拌边加热将乙酸乙酯挥发后即制成样品。利用爆发点测试仪测试其热爆发温度Tb,结果见表1。

表1 RDX 基含铝炸药配方及热爆发动力学参数Table 1 Formulation and kinetic parameters of heat explosion for RDX-based aluminized explosives
2 结果与讨论
2.1 RDX 含量对热爆发活化能的影响
根据热爆发方程计算热爆发温度[8]的同时,计算出该RDX 基含铝炸药体系的热爆发动力学参数Eb与lnA,结果见表1。热爆发方程为:

式中:τ为爆发延滞期,s;A为指前 因子,s;Eb为试样的热爆发活化能,kJ/mol;R为摩尔气体常数,8.314kJ/(mol·K);T为试验温度,K。
用表1 数据作热爆发活化能Eb与RDX 含量的关系曲线,如图1 所示。由图1可看出,随着RDX 含量的逐渐增加,其热爆发活化能Eb先缓慢降低,在RDX 质量分数为80%左右,Eb降到最低点,其后Eb随着RDX 含量的增加而升高。这与热爆 发温度Tb和RDX含量关系[8]相似。可见,RDX和铝粉含量对热爆发活化能Eb有显著的影响。

图1 Eb与RDX 含量之间的关系Fig.1 Relation between Eband RDX content
2.2 热爆发动力学参数的补偿效应
将表1中指前因子的对数(-lnA)与热爆发活化能(Eb)作线性回归,结果见图2。由图2可看出,两者有极好的线性关系,几乎所有的数据点都落在回归直线上,即热爆发活化能Ea与相应的指前因子的对数lnA之间存在着“动力学补偿效应”。获得的动力学补偿方程为:

式中:a1=0.081 3;b1=0.194 5×10-3mol/J;线性相关系数r=0.995 9。

图2 RDX基含铝炸药的热爆发动力学补偿效应Fig.2 Kinetic compensation plot for heat explosion of RDX-based aluminized explosives
2.3 热爆发活化能与组分含量关系的理论分析
由文献[8]获得热爆发温度Tb与RDX 和铝粉含量的关系方程:
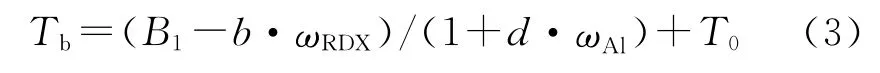
式中:d为经验常数;B1和b为常数。
由于存在动力学补偿效应,可将式(2)(动力学补偿方程)代入热爆发方程式(1),整理后得:因为在5s延滞期热爆发温度Tb下,τ=5s,因此式(4)中的C为常数。
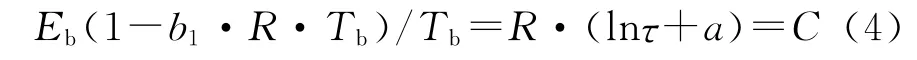
为了获得Eb与RDX 含量(ωRDX)和铝粉含量(ωAl)的关系,将式(4)两边分别与式(3)两边相乘得:

式中:a2=C·B1和b2=C·b。
式(6)或式(7)即为热爆发活化能Eb与RDX含量(ωRDX)和铝粉含量(ωAl)的关系式。
2.4 热爆发活化能与组分含量理论关系式的实验验证
根据热爆发温度Tb与RDX 含量(ωRDX)和铝粉含量(ωAl)的试验回归方程[8]:

获得B1=1506,b=13.42,d=5,而此处室温设为T0=300K。
把表1中ωRDX对应的Tb值代入方程(8),可获得对应的B2值,同时从d=5和对应的Eb值可求得式(6)左边项B2·Eb·(1+d·ωAl)的对应值,结果见表2。
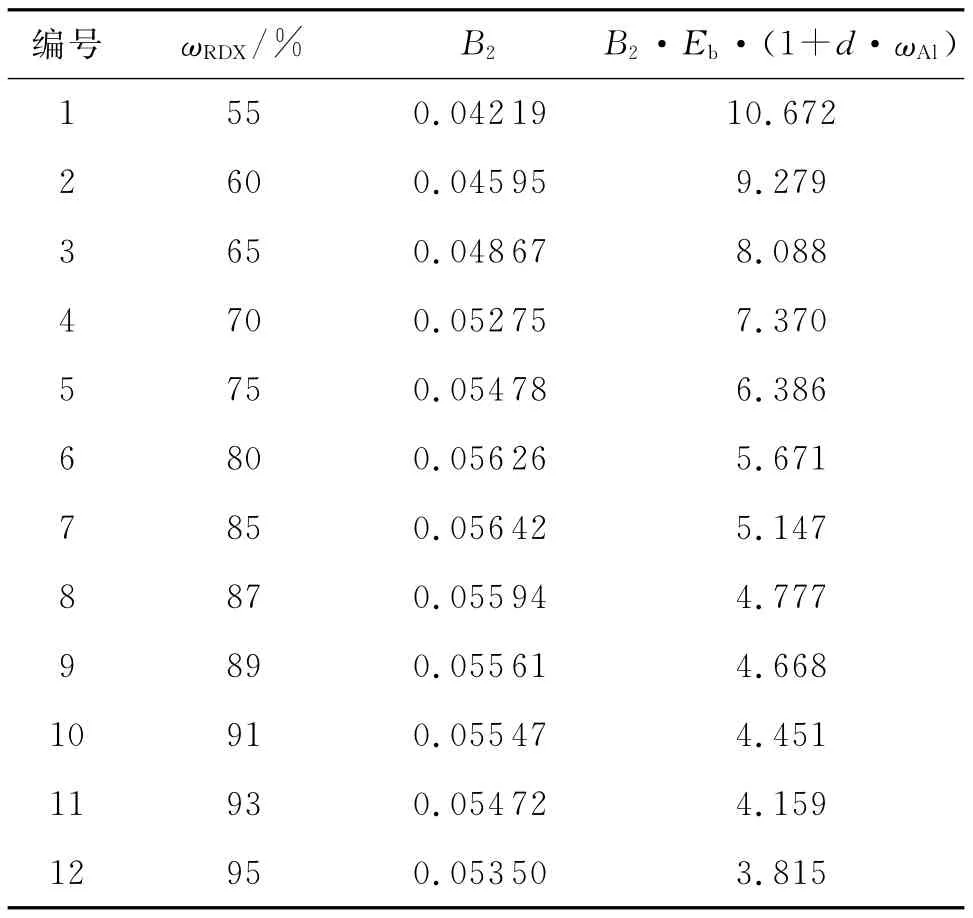
表2 RDX 基含铝炸药的热爆发参数Table 2 Heat explosion parameters for RDX-based aluminized explosives
用表2中B2·Eb·(1+d·ωAl)的数据与RDX含量ωRDX作线性回归分析,获得的曲线见图3。所得的线性关系式为:

显然,B2·Eb·(1+d·ωAl)与RDX含量之间有较好的线性关系,因此,方程(6)或(7)可以描述RDX基含铝炸药热爆发活化能与组分含量的关系。

图3 Eb与铝粉含量的理论关系曲线Fig.3 Theoretical relationship between Eband Al content
3 结 论
(1)随着RDX 含量的增加,RDX 基含铝炸药的热爆发活化能Eb先下降后升高,约在RDX 质量分数为80%时,达到最小值。
(2)RDX 基含铝炸药的热爆发动力学参数lnA和Eb之间存在动力学补偿效应。
(3)根据热爆发温度Tb与RDX 和铝粉含量的关系以及动力学补偿效应,从理论上导出了热爆发活化能Eb与RDX 和铝粉含量的关系方程。
(4)从实验数据获得了表示热爆发活化能Eb与RDX 含量和铝粉含量的关系方程,同时也验证了该关系的理论方程。
[1]刘子如.含能材料热分析[M].北京:国防工业出版社,2008.
[2]Svatopluk Z.Kinetic compensation effect and thermolysis mechanisms of organic polynitroso and polynitro compounds[J].Thermochimica Acta,1997,290:199-217.
[3]刘子如,阴翠梅,刘艳,等.RDX 和HMX 的热分解II.动力学参数和动力学补偿效应[J].火炸药学报,2004,27(4):72-75.
LIU Zi-ru,YIN Cui-mei,LIU Yan,et al.Thermal decomposition of RDX and HMX II.Kinetic parameters and kinetic compensation effects[J].Chinese Journal of Explosives and Propellants,2004,27(4):72-75.
[4]Cremer E.Compensation effect in heterogeneous catalysis[J].Adv Catal,1955,7:75-91.
[5]Gallagher P K,Johnson D W Jr.Kinetics of the thermal decomposition of CaCO3in CO2and some observation on the kinetic compensation effect[J].Thermochim Acta,1976,14:255-261.
[6]Dollimore D,Rodgers P F.The appearance of a compensation effect in the thermal decomposition of manganese(II)carbonates,prepared in presence of other metal ions[J].Thermochim Acta,1979,30:273-280.
[7]Brill T B,Gongwer P E,Williams G K.Thermal decom-position of energetic materials 66.Kinetic compensation effects in HMX,RDX,and NTO[J].J Phys Chem,1994,98:12242-12247.
[8]郑亚峰,常 海,刘子如,等.RDX 和铝含量对RDX 基含铝炸药热爆发温度的影响[J].火炸药学报,2011,34(4):49-51.
ZHENG Ya-feng,CHANG Hai,LIU Zi-ru,et al.Effect of RDX and Al contents on the heat explosion temperature for RDX-based aluminized explosives[J].Chinese Journal of Explosives and Propellants,2011,34(4):49-51.
