常用时频分析方法在数字地震波特征量分析中的应用①
2011-01-27姚家骏杨立明冯建刚
姚家骏,杨立明,冯建刚
(1.青海省地震局,青海 西宁 810000;2.中国地震局兰州地震研究所,甘肃 兰州 730000)
0 引言
对于频率等特征量不随时间变化的平稳信号,传统的傅立叶变换就能很好地建立时域与频域的映射关系。而对于地震波等非平稳信号,由于其频率等特征量随时间变化而变化,传统的傅立叶变换因为不能反映信号的时频局域性信息不再适用。用时频分析法建立起时间和频率的二维函数将一维的时间域信号(如数字化地震波记录)扩展到二维的时频平面上,直观而全面地反映信号频率随时间的变化关系,使我们同时掌握信号的时域及频域局域性信息。
时频分析方法可分为线性与非线性两种[1]。其中线性时频表示是由傅立叶变换转化而来,典型的线性变换形式有短时傅立叶变换(STFT)、小波变换(WT)及S变换。常用的非线性时频表示有维格纳-威尔分布(WVD)、乔伊-威廉斯分布(CWD)、赵-阿特拉斯-马克斯时频分布(ZAM)等。非平稳信号分析与处理的研究工作主要是从20世纪40年代开始的。1946年Gabor[2]首次发现在信号处理的过程中时频分析的重要性,随后他便提出用加窗傅立叶变换(STFT)法去找出声波频率的确切位置;Wigner于1932年首先提出了Wigner分布的概念,并把它用于量子力学领域;1948年Ville[3]首先把它应用于信号分析,因此Wigner分布又称Wigner-Ville分布,简称为 WVD;1966年Cohen[4]给出了各种双线性时频分布的统一表示形式;1996年Stockwell提出一种介于STFT和小波变换之间的S变换[5],吸取了两者的优点。近几年来人们利用时频分析技术识别弱震相、区分人工地震与天然地震、研究大震前小震的频谱变化等已经做了一些工作[6-11]。本文试用短时傅立叶变换(STFT)、S变换、CWD分布以及人们较少关注的ZAM分布分析数字地震波P波信号、S波信号的时频分布,分析它们在分辨地震波时的应用效果,总结其优缺点。
1 时频分析的算法原理
1.1 短时傅立叶变换(STFT)
短时傅立叶变换(STFT)思路依托于处理平稳信号的经典傅立叶变换,其基本思想[1]是把信号划分成许多小的时间间隔,用傅立叶变换分析每一个时间间隔,以便确定每个时间间隔所存在的频率,沿时间发展的这些频率的总体就表现频谱在时间上的变化过程。短时傅立叶变换概念直接,算法简单,是其他时频方法的基础。
信号s(t)的STFT 定义[12]为

其中h(t)是窗函数,反变换的公式为

由式(1)可知,短时傅立叶变换就是在傅立叶变换的基础上通过固定长度的滑动窗来计算信号频谱的。但该滑动窗口与频率无关,它的时间分辨率和频率分辨率受Heisenberg测不准原理约束,利用短窗口,时间分辨率比较好,但是频率分辨能力差;当利用长窗口时,有较高的频率分辨率,但时间分辨能力就弱。
1.2 S变换
信号s(t)的S变换(ST)的定义[5]为

式中τ、f分别表示时间和频率,均为实数。反变换为

它是以Morlet小波为基本小波的连续小波变换的延伸。基本小波是由简谐波与高斯函数的乘积构成的,定义为

基本小波中的简谐波在时间域仅作伸缩变换,而高斯函数则进行伸缩和平移。由式(2)可知,S变换也可以看作是在傅立叶变换的基础上通过滑动窗来计算信号频谱的,但滑动窗口与频率有关。S变换采用宽度可变的高斯窗函数,其时窗宽度随频率呈反比变化,在低频段的时窗较宽,可获得较高的频率分辨率;而高频段的时窗较窄,可获得很高的时间分辨率。因此,较之STFT,S变换具有更好的时频分辨率,特别是在高频部分S变换的时间分辨率优势更加明显。而在连续小波变换中简谐波与高斯函数进行同样的伸缩和平移。因此与小波变换、短时Fourier变换等时—频域方法相比,S变换有其独特的优点,如信号的S变换的时频谱分辨率与频率(即尺度)有关,且与其Fourier谱保持直接的联系,基本小波不必满足容许性条件[5]等,这些特点在实际应用中是非常有用的。
1.3 乔伊-威廉斯分布(CWD)
非线性时频变换中最基本的的Wigner-Ville分布(WVD)[5]为

其中*表示解析信号s(t)的复共轭,s(t)在信号分时出现两次,因此称其为双线性变换。由于式中不包含任何的窗函数,避免了线性时频表示中时间、频率分辨率相互牵制的矛盾。虽然WVD的时频聚集度最高,能满足的数学性质最多,但多信号的WVD会出现交叉项,在不少场合会限制其效果。后来人们又提出多种改进形式,如指数分布、广义指数分布、广义双线性时频分布(Cohen类时频分布)等,因此 WVD被誉为 “所有时频分布之母[13]”。
20世纪60年代中期,Cohen将众多的双线性时频分布统一为一种形式,习惯称之为Cohen类时频分布,定义[14]为


其中φ(θ,τ)叫做核函数。
选取不同的核函数可得到不同的时频表示.但核函数在减少交叉项的同时也会带来负面作用:信号自身项展宽,信号分辨率的降低。抑制交叉项与提高信号分辨率,如同短时傅立叶变换中时域和频域分辨率一样,不可能同时做到最好,只能折中最优。目前大多抑制交叉项的方法是以降低分辨率为代价的。分析地震信号时频分布,需要寻找一个适应于地震信号性质的滤波核函数,最大地抑制交叉项同时尽可能小地降低分辨率。对于乔伊-威廉斯时频分布,取核函数

CWD可以有效的抑制由不同时间和不同频率中心引起的交叉干扰,但是它不能减少同一频率不同时间中心或是同一时间不同频率中心之间的干扰。而且,CWD的计算机处理速度较慢,交叉项的出现常常导致时频平面上出现伪影现象。
1.4 赵-阿特拉斯-马克斯时频分布(ZAM)
若取核函数

则Cohen类时频分布变为赵-阿特拉斯-马克斯时频分布(ZAM)。在赵-阿特拉斯-马克斯原著中g(τ)=1,α=1/2。研究表明[15]类似形如式(8)的锥形核函数很好的适合于地震数据分析。这个核函数不像频谱图那样消除脉冲,但可完全地抑制它们,从而得到一个有效和准确的频率局部化表示。
2 算例分析
选用四个基本高斯元构成一个合成信号,时间长度为128s,其特征见表1。

表1 四个基本高斯元的特征情况
为了较好地在不同TFD方法下考察信号间的相干扰程度,设计出一对信号在同一时间中心,另一对在同一频率中心,并且相邻(图1)。其中图1(a)为合成信号的时域波形,图1(b)为合成信号理想情况的时频分布图。

图1 合成信号及其理论上的时频分布Fig.1 Synthesis signal and its academic TFD.
合成信号的短时傅立叶变换(STFT)、S变换、乔伊-威廉斯时频分布(CWD)、赵-阿特拉斯-马克斯时频分布(ZAM)如图2所示。由于STFT的时频分辨率与窗函数长度有很大的关系,我们经过实践,选取合理的长度,以便同时在时间分辨率、频率分辨率上取个折中。由图2(a)、图2(b)的色彩显示可以看出,对于STFT来说,信号频谱图在频率方向上对应的宽度是不变的,即在低频和高频的频率分辨率是不变的,不利于低频、高频信号的分辨。对于S变换来说,信号频谱图在频率方向上对应的宽度是不同的,可看到在信号频率变化处有较明显的边界,能把高频信号分离出,并且不存在交叉干扰。S变换在低频部分具有较高的频率分辨率,高频部分具有较高的时间分辨率。恰恰能满足法国地球物理学家Morlet于20世纪80年代初在分析地震信号时提出的“地震信号的低频端应该具有很高的频率分辨率,而在高频端频率分辨率可以较低”的要求。但信号的时频聚集性较差。图2(c)所示CWD时频分布尽管具有较好的时频聚集性,有明显的交叉项干扰。信号的ZAM时频分布(图2(d))同样具有较好的时频聚集性,而且和已知仿真信号时间起始点和频率点相比,交叉项干扰要小于CWD时频分布结果,但时频聚集性稍微不如CWD。
3 数字化地震波记录时频分析
甘肃省平凉数字地震台记录的2009年11月28日四川成都彭州市MS5.0地震,震相清晰无干扰。仪器的采样率为100。截取其UD道P波、S波,如图3、图4,用上述四种方法做TFD。由图3(a)可以看出,该P波信号的11.8s到13.5s、18.5~19.5s之间是振幅较大的区域。由图3(b)的傅立叶谱可以看出,该P波信号的主频率为1.9Hz,主要分布在1.5~3Hz之间。由图4(a)可以看出,该S波信号的5.5~7.1s、17.5s到20s之间是振幅较大的区域。由图4(b)的傅立叶谱可以看出,该S波信号的主频率为0.7~0.9Hz,主要分布在1.7 Hz之内。图5可知:四种方法都能较准确地检测出该信号的主频率的时频位置,但S变换能检8Hz的高频弱信号,其余三种方法只能检测到4~5Hz左右的高频信号;非线性的CWD法与ZAM法的时频聚集性强,主信号的时频分布情况一目了然;CWD时频分布尽管具有较好的时频聚集性,但交叉项干扰比较明显,容易出现伪影现象,产生虚假频率;ZAM法虽时频聚集性稍逊于CWD时频分布,但在消除交叉项的干扰的优势上比较明显。

图2 合成信号的时频分布Fig.2 TFD of the synthesis signal((a)STFT;(b)ST;(c)CWD;(d)ZAM).

图3 地震波P波信号及其傅立叶谱Fig.3 P wave(a)and its Fourier spectrum (b).

图4 S波及其傅立叶谱Fig.4 S wave(a)and its Fourier spectrum (b).

图5 P波的时频分布Fig.5 TFD of P wave((a)STFT;(b)ST;(c)CWD;(d)ZAM).
图6为该S波信号经短时傅立叶变换(STFT)、S变换、乔伊-威廉斯时频分布(CWD)、赵-阿特拉斯-马克斯时频分布(ZAM)所做得时频分布。由图6可知:四种方法都能较准确地检测出该信号的主频率的时频位置,但S变换能检2~3 Hz的高频弱信号,其余三种方法只能检测到2s左右出现的1.7Hz左右的高频主信号;非线性的CWD法与ZAM法的时频聚集性的优势依然很明显;但仍然知道CWD时频分布虽然具有较好的时频聚集性,可交叉项干扰比较明显的;相对于CWD法,ZAM法具有消除交叉项的干扰的优势。
4 结论
通过对模拟信号以及平凉数字地震台记录的2009年11月28日在四川彭州市MS5.0地震P波、S波的分析可知:
(1)四种方法都能比较精确地检测出地震信号的主频率的时频位置,二维时频分布图能充分显示出地震波信号的非稳定性特征;
(2)线性的STFT法运算速度最快,但时频分辨率表现最差;S变换在检测高频弱信号方面有独特的优势,但时频聚集性较差;
(3)在对信号的时频聚集性方面,非线性的CWD法与ZAM法远比线的STFT、S变换方法要强;
(4)CWD时频分布尽管具有较好的时频聚集性,但交叉项干扰比较明显,容易出现比较明显的伪影现象,产生虚假频率,ZAM法虽时频聚集性稍逊于CWD时频分布,但在消除交叉项的干扰方面要远比CWD法出色。
数字化地震观测技术的普及与提高,使现代信号处理技术能得以很好的比较与应用。时频分析可以在时频二维平面很好地解释地震波的非平稳性,可以更丰富地显示地震波特征,因此时频分析在地震震相识别、模式识别以及利用小震频谱特征预报大地震等方面有广泛的应用前景。
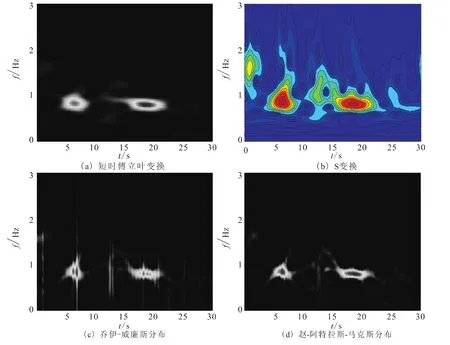
图6 S波的时频分布Fig.6 TFD of S wave((a)STFT;(b)ST;(c)CWD;(d)ZAM).
[1]L科恩(美).时频分析-理论与应用[M].西安:西安交通大学出版社,1998.
[2]Gabor D.Theory of communication[J].Journal of the IEEE,1946,93:488-497.
[3]Ville J.Theorie et application de la notion de signal analytique[J].Cables et transmissions,1948,2A:61-74.
[4]Cohen L.Generalized phase-space distribution functions[J].Jour.Math.Phys.,1966,7:781-786.
[5]R Stockwell,L Mansinha,R Lowe.Localization of the Complex Spectrum:The S Transform[J].IEEE Trans.on Signal Process,1996,44(4):998-1001.
[6]许康生.地震信号的时频分析[J].西北地震学报,2000,22(4):479-482.
[7]刘希强,周惠兰,李红.基于小波包变换的地震数据时频分析方法[J].西北地震学报,2000,22(2):143-146.
[8]刘希强,沈萍,山长仑,等.数字化地震波形资料的时频分析方法及应用[J].西北地震学报,2004,26(2):118-125.
[9]熊晓军,贺振华,黄德济,等.广义S变换在地震高分辨处理中的应用[J].勘探地球物理进展,2006,29(6):415-418.
[10]陈学华,贺振华.改进的S变换及在地震信号处理中的应用[J].数据采集与处理,2005,20(4):449-453.
[11]严锋,靳平,范广超.地震台阵上信号方位角和慢度的时、频域估计方法比较[J].西北地震学报,2006,28(4):227-230.
[12]赵淑红.时频分析方法及其在地震数据处理中的应用[D].西安:长安大学,2006.
[13]张建,沈民奋,宋骥.三种时频分析方法在心音信号分析中的应用[J].汕头大学学报(自然科学版),2003,18(2):62-69.
[14]王红萍.非平稳信号时频分析方法性能研究[D].南京:南京航空航天大学,2008.
[15]张晔.信号时频分析及应用[M].哈尔滨:哈尔滨工业大学出版社,2006.
