低温下XXZ反铁磁自旋链的自旋波谱

成泰民， 葛崇员， 李青云

(沈阳化工大学数理系，辽宁沈阳110142)

其中η=J┷/Jz.根据(8)式、(15)式、(16)式进行约化数值计算可得反铁磁自旋链的自旋波谱(磁振子谱)特性，如图1所示.

最近XXZ反铁磁自旋链的研究取得了新进展［1-5］.特别是对于量子信息的传输及自旋量子态的研究领域取得了进展［1-2］.对此体系的解析解，一般利用量子统计理论进行研究.但是对于低温下的近似解，通常对此种理论模型采用双时格林函数方法及“切断近似法”处理体系的元激发能谱［6-7］.而后利用其关联函数的谱强度表示热力学格林函数，用热力学格林函数及体系的宏观物理量的关系分析其体系的宏观物性.此问题的关键是元激发能谱的求解，但是此方法较繁琐.范洪义创立的不变本征函数法［8-9］处理只包含算符的二次项的Hamiltonian非常便捷［10］.对此我们在非简谐近似下，系统地研究低温下XXZ反铁磁自旋链的自旋波谱，并讨论简谐近似与非简谐近似下的自旋波谱的变化规律.这对进一步研究该体系的宏观物理性质具有关键意义.这是因为体系的元激发能量与体系的内能、磁化强度、磁化率等宏观物理量密切相关.在此文中我们对微扰相关的非线性Hamiltonian进行以简谐近似下自旋波谱的统计平均线性化近似.

1 XXZ反铁磁自旋链的Hamiltonian及自旋波谱

XXZ反铁磁自旋链由自旋朝上的次晶格与自旋朝下的次晶格嵌套构成.设自旋朝上的次晶格与自旋朝下的次晶格各含有N/2个磁性原子(或离子).那么根据双次晶格模型把XXZ反铁磁自旋链的Hamiltonian表示如下［5，7］:

对ai及bi进行点阵傅立叶变换，

再把(2)式和(3)式代入到(1)式，去掉算符的6次幂项可得:

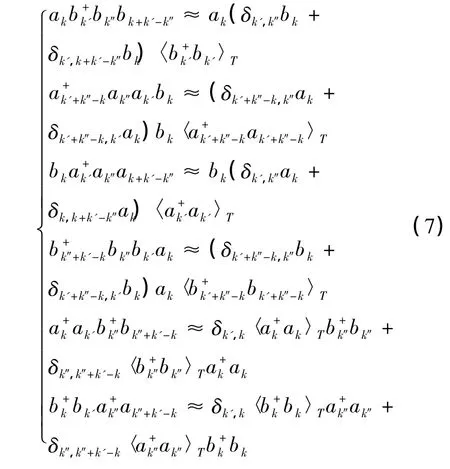
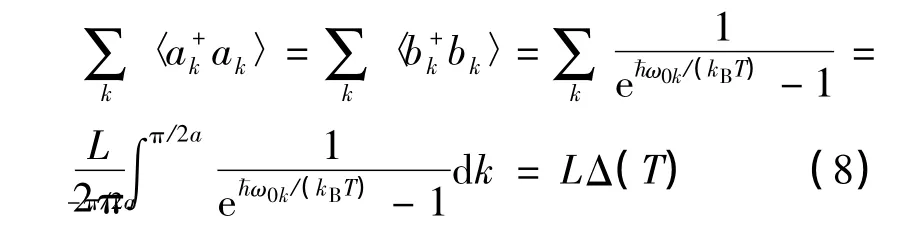
把(7)式、(8)式代入到(6)式，经整理可得:

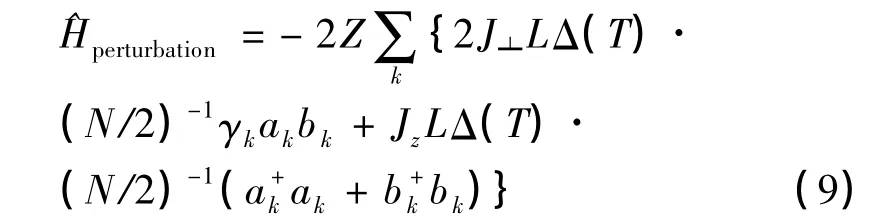
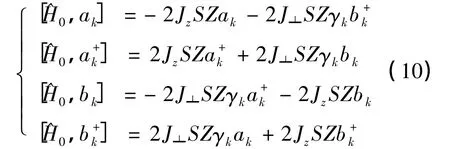
在(10)式中利用了玻色算符的对易律

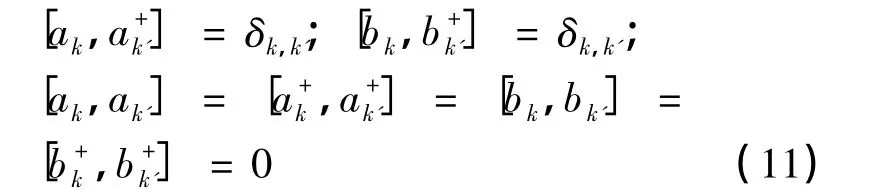
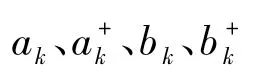
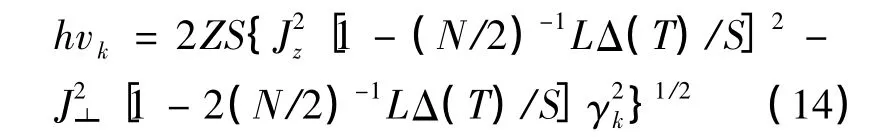
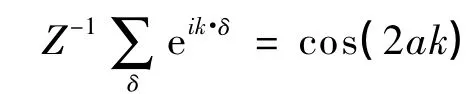
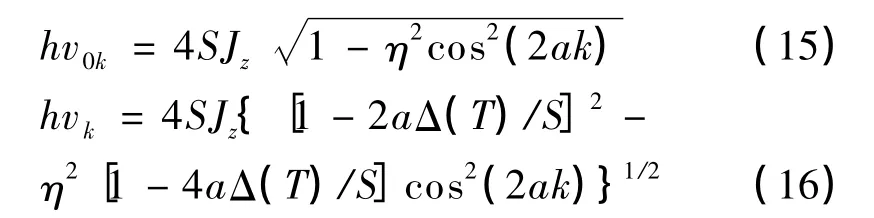
其中η=J┷/Jz.根据(8)式、(15)式、(16)式进行约化数值计算可得反铁磁自旋链的自旋波谱(磁振子谱)特性，如图1所示.

图1 在2ka=π/2处，XXZ反铁磁自旋链的自旋波约化能量差(hvk-hv0k)/(4SJz)随约化温度kBT/Jz的变化Fig.1 The change of the spin wave reduced energy's difference of XXZ anti-ferromagnetic spin chain with the reduced temperature kBT/Jzat 2ka=π/2

图1说明，约化温度kBT/Jz＞0.621 3时，非简谐近似下的反铁磁自旋链的自旋波能量在第一布里渊区不出现软化现象，只有硬化现象，这与约化交换积分 η=J┷/Jz无关.当 kBT/Jz＜0.621 3时，反铁磁自旋链在低温下由磁振子-磁振子耦合作用才能够引起磁振子(自旋波量子)软化现象.并且在约化温度kBT/Jz=0.46附近磁振子软化最明显.当kBT/Jz＜0.46时，随着温度的升高磁振子软化逐渐加强，但是约化温度在0.46＜kBT/Jz＜0.621 3区域，随着温度的升高磁振子软化逐渐减弱.

图2为约化交换积分η=0.4时，在不同的约化温度(kBT/Jz)下XXZ反铁磁自旋链的自旋波约化能量hvk/(4SJz)在第一布里渊区的变化.

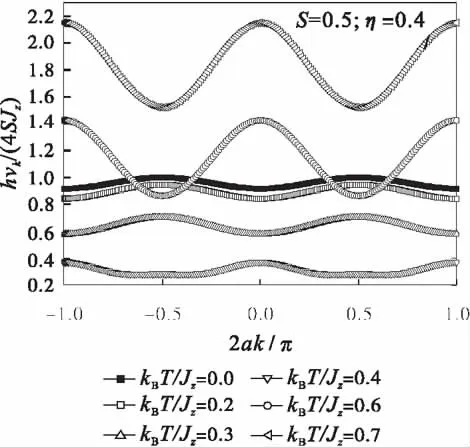
图2 约化交换积分η=0.4时，在不同的约化温度(kBT/Jz)下XXZ反铁磁自旋链的自旋波约化能量hvk/(4SJz)在第一布里渊区的变化Fig.2 When reduced exchange integral η=0.4 the change of the spin waves reduced energy of XXZ antiferromagnetic spin chain in the first Brillouin zone under different reduced temperature(kBT/Jz)

图2再一次说明图1分析的正确性.把约化交换积分固定为η=J┷/Jz=0.4，在不同的约化温度下反铁磁自旋链的磁振子谱的变化规律表明，确实在kBT/Jz＜0.46时，随着温度的升高磁振子软化逐渐加强.但是约化温度在0.46＜kBT/Jz＜0.621 3区域，随着温度的升高，在2ka =π/2点磁振子软化逐渐减弱，而且在布里渊区的2ka=0、2ka=±π附近出现磁振子硬化现象.当kBT/Jz＞0.621 3时在整个布里渊区只有磁振子硬化现象.

图3、图4说明，在第一布里渊区，当约化温度η=J┷/Jz=0.4时，反铁磁自旋链的磁振子谱随不同的约化交换积分常数η=J┷/Jz的变化规律.从而可知当约化交换积分η=J┷/Jz越小，体系的磁振子谱整体软化越明显.

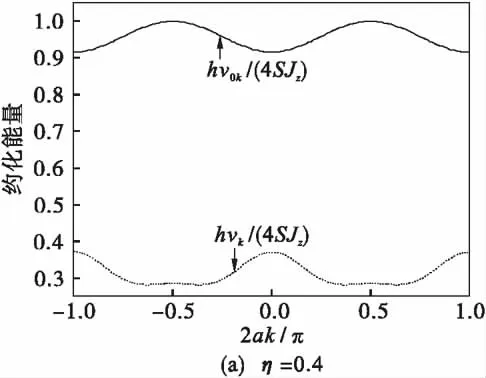
图3 约化温度kBT/Jz=0.4时，XXZ反铁磁自旋链的自旋波约化能量hvk/(4SJz)在第一布里渊区的变化Fig.3 When reduced temperature kBT/Jz=0.4，the change of the spin waves reduced energy hvk/(4SJz)of XXZ anti-ferromagnetic spin chain in the first Brillouin zone

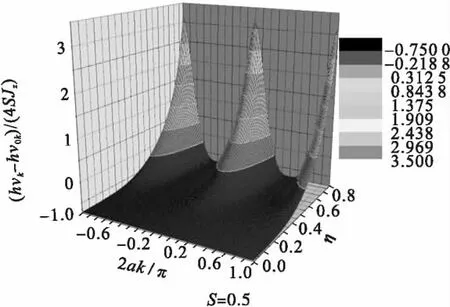
图4 约化温度kBT/Jz=0.4时，XXZ反铁磁自旋链的自旋波约化能量差(hvk-hv0k)/(4SJz)在第一布里渊区随约化交换积分η的变化Fig.4 When reduced temperature kBT/Jz=0.4，the change of the spin waves reduced energy's difference(hvk-hv0k)/(4SJz)of XXZ anti-ferromagnetic spin chain with reduced exchange integral η in the first Brillouin zone

2 结论

利用不变本征算符法研究了XXZ反铁磁自旋链的简谐近似下的自旋波能谱，并与统计平均近似相结合，进一步研究了非简谐近似下的XXZ反铁磁自旋链的自旋波能谱.讨论了XXZ反铁磁自旋链的自旋波谱对各项物理参数的变化规律及不变本征算符法适用范围.

(1)不变本征算符法对于处理线性近似下的哈密顿量非常便利.但是对非简谐哈密顿量必须处理为线性近似后才容易处理系统的元激发能量(如磁振子谱等).

(2)XXZ反铁磁自旋链的自旋波谱与温度密切相关，并有2个转变温度kBT/Jz=0.46和kBT/Jz=0.621 3.

(3)在低温(kBT/Jz＜0.46)下，XXZ反铁磁自旋链的自旋波谱与约化交换积分η=J┷/Jz密切相关.

［1］ Trippe C，Honecker A，Klümper A，et al.Exact Cal-culation of the Magnetocaloric Effect in the Spin-1/ 2 XXZ Chain［J］.Phys.Rev.B，2010，81(5): 054402-1-054402-11.

［2］ Bayat A，Bose S.Information-transferring Ability of the Different Phases of a Finite XXZ Spin Chain［J］.Phys.Rev.A，2010，81(1):012304-1-012304-11.

［3］ Stéphan J M，Furukawa S，Misguich G，et al.Shannon and Entanglement Entropies of One-and Twodimensional Critical Wave Functions［J］.Phys. Rev.B，2009，80(8):184421-1-184421-24.

［4］ Laforencie N，Rieger H，Sandvik A W，et al.Crossover Effects in the Random-exchange Spin-1/2 Antiferromagnetic Chain［J］.Phys.Rev.B，2004，70 (5):054430-1-054430-11.

［5］ Nagaosa N.Quantum Field Theory in Strongly Correlated Electronic Systems［M］.北京:世界图书出版公司北京公司，2010:1-21.

［6］ 蔡建华，龚昌德，姚希贤，等.量子统计的格林函数理论［M］.北京:科学出版社，1982:195-227.

［7］ 李正中.固体理论［M］.北京:高等教育出版社，2002:68-70，80，84.

［8］ Fan H Y，Li C.Invariant‘Eigen-operator’of the Square of Schrödinger Operator for Deriving Energy-level Gap［J］.Phys.Lett.A，2004，321(2):75 -78.

［9］ Fan H Y，Wu H.Deriving Vibrating Modes of Some Multiatom Molecules by Virtue of the Invariant Eigenoperator Method［J］.Modern Physics Letters B，2005，19(26):1361-1366.

［10］成泰民，葛崇员，李青云，等.不变本征算符法计算各向异性Heisenberg反铁磁系统的自旋波能量［J］.沈阳化工大学学报，2011，25(2):170-173.

［11］ Dyson F J.General Theory of Spin-wave Interactions［J］.Phys.Rev.，1956，102(5):1217-1230.

［12］Cheng T M，Li L，Xianyu Z.Magnon-damping in Two-dimensional Heisenberg Ferromagnetic System［J］.Physics Letters A，2006，353(5):431-438.