抗震分析反应谱法和时程分析法数值仿真比较①

2011-01-25吴小峰孙启国狄杰建周迎春

地震工程学报 2011年3期

吴小峰，孙启国，狄杰建，周迎春

（北方工业大学机电工程学院，北京 100141）

0 前言

目前地震反应分析方法主要分为静力法、反应谱法和时程分析法［1］。静力法实质上不考虑结构的动力特征，现在在工程抗震分析上应用较少；反应谱法操作相对较为简单，现被多国抗震规范推荐使用；时程分析法动态模拟较为准确，但其计算量大，通常应用于特别重要结构或不规则结构或其他特殊情况。反应谱法理论上只适用于弹性结构的抗震分析，用于非弹性情况必须进行修正，而时程分析法可直接应用于弹塑性结构的抗震分析计算。我国抗震规范推荐采用反应谱法和时程分析法［2］。本为通过分析反应谱法和时程分析法的计算原理，运用ANSYS有限元软件，以一工程实例的抗震反应计算结果为基础，讨论反应谱法和时程分析法数值仿真上的共同性和计算结果的一致性。

1 算法原理

1.1 反应谱法

反应谱法是将动力问题转化为静力问题来计算，应用结构总响应是各振型响应叠加的原理。反应谱法首先根据地震波时程记录构造反应谱，再依据反应谱计算结构各阶振型的最大响应，然后通过一定的模态合并算法计算总的最大响应［1，3］。可应用ANSYS谱分析中的单点响应谱分析法辅助计算，它是反应谱理论的工程应用。在模态合并算法上依据我国抗震规范推荐用的算法平方和开方的组合算法。

第i阶模态上的最大响应

其中：Ri为第i阶模态上的最大响应；ψi为第i阶模态的振型向量；Ai为第i阶模态的模态系数。Ai的大小取决于第i阶模态的反应谱值和第i阶模态的参与系数。参与系数是每阶模态在特定方向上对变形贡献大小的度量。

平方和开方的组合算法的一般形式

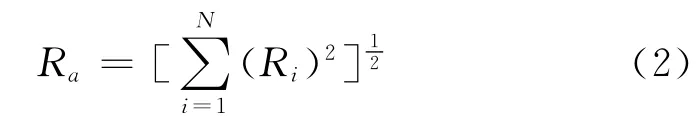
其中：Ra为合并后的模态总体响应；N为参加合并的模态数目。

地震反应谱曲线具体反映了地震动特性，模态振型反映了结构的动态特性，可见反应谱法体现了地震动特性和结构动态特性对结构地震响应的影响。

1.2 时程分析法

时程分析法，也称直接动力法，它是根据动力学运动方程，将地震波时程记录作为激励，直接积分求解结构在各个时刻的动态响应。可应用ANSYS瞬态分析中的完全法辅助计算，它依据直接动力分析理论，积分算法采用Newmark时间积分法。

动力学基本运动方程

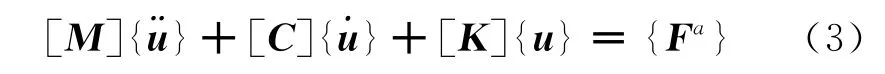
其中：［M］为质量矩阵；［C］为阻尼矩阵；［K］为刚度矩阵为节点加速度向量；为节点速度向量；｛u｝为节点位移向量为载荷向量。

地震波时程记录全面的反映了地震动特性，以此作为激励积分计算结构的动态响应，可见时程分析法全面体现了地震动特性和结构动态特性对结构地震响应的影响。

1.3 算法比较

反应谱法的优点是计算方便，计算量小，可有效的计算结构地震响应的最大值。但反应谱法原则上只适用于线性结构，地震反应谱不包含相位的信息，计算精度取决于参与合并振型的数目。时程分析法可模拟结构在整个地震持续时间内各时刻的地震响应，可成功的处理各种非线性问题，但其计算量大，地震响应计算值较大依赖于地震波时程曲线的选取［4］。

反应谱法实质是振型分解的算法，时程分析法是积分算法，但反应谱法和时程分析法均体现地震动特性和结构动态特性对结构地震响应的影响。假设结构地震反应是线性问题，采用同一地震波，即地震波时程曲线和反应谱曲线相对应，则反应谱法和时程分析法计算的结构地震响应具有一定程度的可比较性。

2 工程实例

2.1 建模

对某高压直流输电换流阀塔建立简化结构模型。塔为四层悬吊式，顶端由U型螺栓固定，各层间由吊杆连接，上端由U型螺栓连接，下端由铰链连接，各层承重50kg。吊杆长3.215m，直径0.03 m；纵梁长4.85m；横梁长1.85m；框梁截面0.065 m×0.12m，承重梁截面0.04m×0.085m；吊杆和承重梁弹性模量8×109Pa，泊松比0.25，密度2100 kg／m3；框梁弹性模量2.1×1011Pa，泊松比0.3，密度7800kg／m3。在抗震分析中，结构材料视为理想的线弹性材料，阻尼比假定0.05。输入天然的El Centro地震波，只考虑水平地震激励。El Centro地震波加速度记录和加速度反应谱见图1。

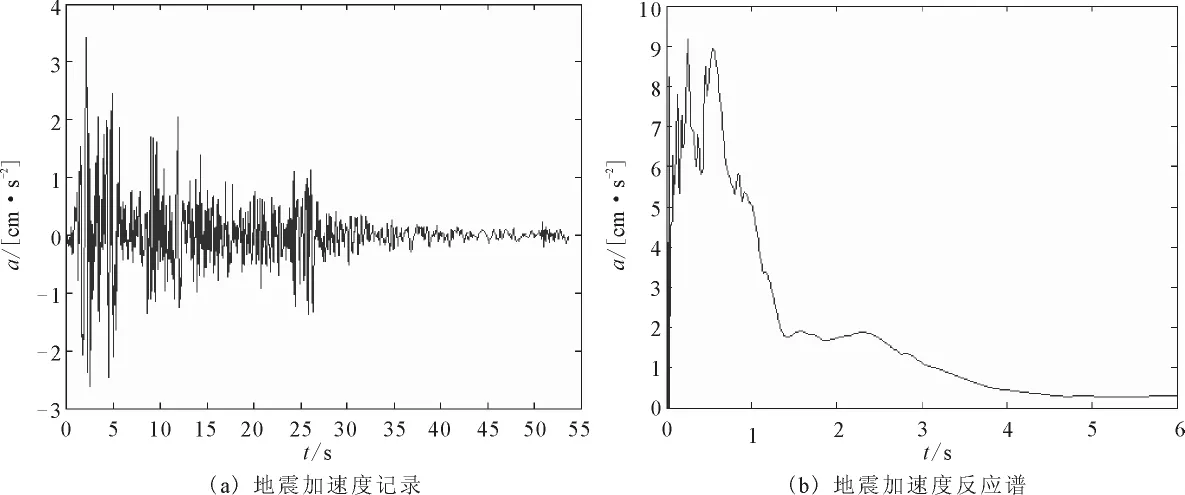
图1 El Centro地震波Fig.1 El Centro wave.

在ANSYS中建立有限元模型，见图2。框梁和吊杆选用BEAM188单元；U型螺栓和铰链选用MPC184中的GENERAL JOINT单元；选用MASS21单元等效承重。BEAM188单元默认是三维线性梁单元，基于Timoshenko理论并考虑了剪切变形的影响，2个节点各有6个自由度，即X、Y、Z方向的平动和绕X、Y、Z轴的转动；MPC184单元是一类多点约束单元，其中GENERAL JOINT是2个节点的连接单元，默认6个自由度，可指定约束的自由度以实现不同连接方式的模拟；MASS21单元是点单元，6个自由度，每个方向可以指定不同的质量和转动惯量。建立几何模型，并划分网格，指定整体单元尺寸大小0.300m。共计划分单元714个，660个节点。

2.2 计算流程

在有一定承重的柔性悬挂结构中重力因素影响显著，故考虑重力作用下的预应力影响。由于在模型中应用了MPC184单元，所以考虑大变形效果的作用。在ANSYS中反应谱法和时程分析法的计算流程如下：

反应谱法计算流程：（1）静力分析，计算重力作用下的预应力；（2）模态分析，并考虑预应力；（3）单点响应谱分析；（4）模态扩展；（5）合并模态；（6）结果后处理。在模态分析中提取前30阶模态，模态扩展20阶模态。在单点响应谱分析中，谱类型选择加速度反应谱，激励方向为X向，设置阻尼比为0.05。

时程分析法计算流程：（1）静载荷步分析，考虑重力产生的预应力；（2）施加地震载荷求解；（3）后处理分析。在静载荷步分析中，施加重力加速度，关闭时间积分效果，打开应力钢化效果，并设置极小的时间值；在后面的地震荷载求解分析中应用矩阵参数法实现多步载荷的求解，不删除重力加速度，打开时间积分效果，设定瑞利阻尼，指定载荷为递增载荷，激励方向为X向。通过文献［5］计算阻尼的方法，求得瑞利阻尼系数α＝0.0694，β＝0.0303。

2.3 计算仿真比较

在换流阀顶端由U型螺栓固定连接，故在顶端节点上约束3个平动的自由度，施加地震载荷并分别进行反应谱法和时程分析法的抗震分析计算，在计算结果中提取结构顶层和底层角点处（图2中①、②点）的地震响应值，只取激励方向上的响应位移值。

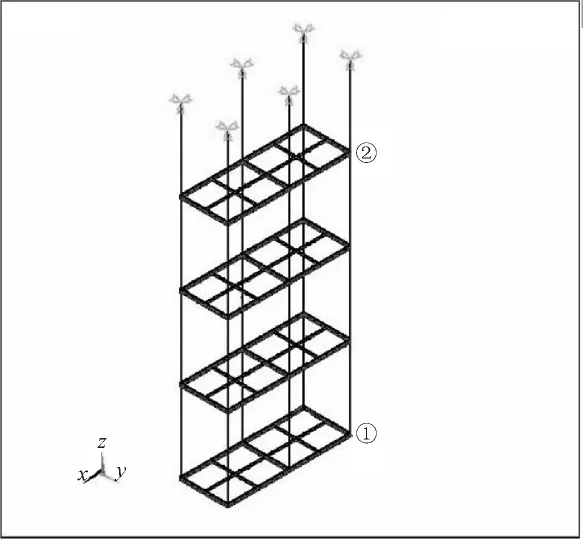
图2 有限元模型Fig.2 Finite element model.

2.3.1 响应位移比较

在反应谱法计算的结果中提取选择角点的总响应位移值，得①号角点总响应位移值0.1055m，②号角点总响应位移值0.4039m；在时程分析法计算的结果中提取选择角点的各时刻的响应位移值，绘制响应位移曲线，得响应位移峰值，见图3和表1。相对误差值是反应谱法和时程历程法计算的响应最值的偏差除以反应谱法计算的总响应值的商。

表1 响应位移值比较

可见，反应谱法计算的总响应位移值与时程分析法计算的响应位移峰值在数值上很接近，相对误差很小，二者仿真结果具有一致性。反应谱法和时程分析法计算的地震响应实质上都是在地震波载荷下结构的动态响应，它们在响应值的影响因素上都同样考虑了结构动态特性和地震动特性，故此它们在计算的响应最值上相一致。二者计算产生误差的原因主要是输入激励存在的不确定性［6］和计算过程产生的误差。

2.3.2 响应频率比较

根据振型叠加原理，结构动态总响应是结构各阶振型响应的叠加，并且引起结构共振的振型贡献最大。在反应谱法计算结果中提取各阶振型的模态系数和振型矢量，计算各阶振型的响应值，并根据计算响应值的大小确定结构共振的主要响应频率，各阶振型的响应值是模态系数与振型矢量的乘积。在时程分析法计算的结果中，对提取的时域响应曲线作傅氏变换，绘制结构响应的频谱特征曲线，并以此确定结构共振的主要响应频率。本文对前两个主要响应频率进行了对比，见图4和表2。

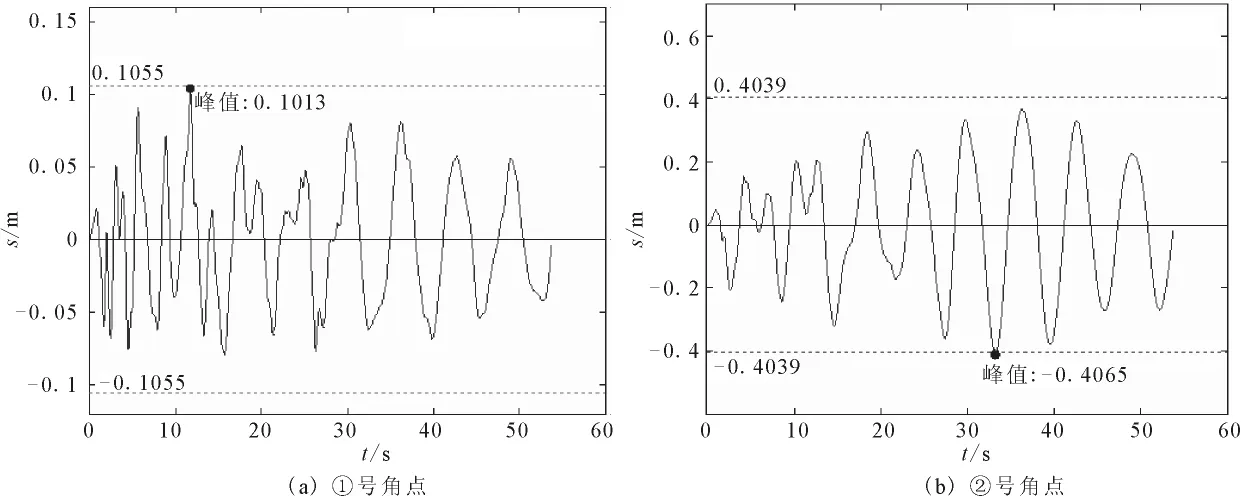
图3 时程分析法的响应位移曲线Fig.3 Response displacement curves of the time history analysis.

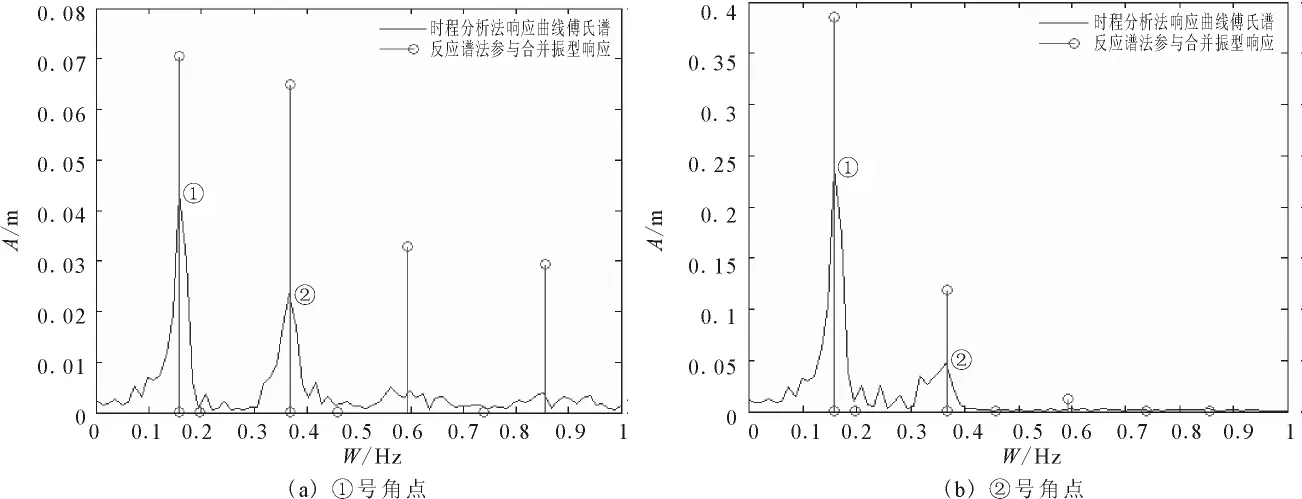
图4 两种方法的主要响应频率对比Fig.4 Comparison of response frequencies between the two metods.

表2 主要响应频率比较

可见，反应谱法和时程分析法中确定的结构主要响应频率在数值上相一致。结构共振是由激励频率与结构固有频率相接近而引起的，反应谱法和时程分析法计算地震响应中均反映了此现象。但是此种数值上的接近存在局限性，在时程分析法中共振频率的识别与激励类型关系密切，冲击型的激励才比较容易识别，这也是产生误差的主要原因。