含非贯穿直裂纹管道局部柔度系数的广义解研究

胡家顺，孙文勇，刘 朵，周 晶

(1.中国石油集团安全环保技术研究院安全技术研究所，北京 100083;2.大连理工大学 海岸和近海工程国家重点试验室，大连 116024)

含非贯穿直裂纹管道局部柔度系数的广义解研究

胡家顺1，孙文勇1，刘 朵2，周 晶2

(1.中国石油集团安全环保技术研究院安全技术研究所，北京 100083;2.大连理工大学 海岸和近海工程国家重点试验室，大连 116024)

基于局部柔度的裂纹模型研究已受到普遍关注，然而，针对含任意方向角裂纹管道的局部柔度系数理论研究鲜有报道。根据线性断裂力学理论推导了含任意方向角非贯穿直裂纹管道在轴力、剪力和弯矩等荷载作用下的局部柔度方程，考虑了方向角变化对弯矩引起局部柔度系数的影响。利用适应性Simpson方法编写了数值积分程序进行局部柔度系数求解，并与Naniwadekar等人试验结果进行了对比分析。研究结果表明:提出的局部柔度系数求解方法准确，为含任意方向角裂纹管道的振动分析提供了基础。

振动分析;局部柔度;管道;裂纹;裂纹方向角

对于工程结构、机械设备，在静动力荷载的长期作用下，随着材料的腐蚀、老化，出现裂纹损伤不可避免。随着结构、设备服役年限的增长，裂纹损伤的累积和扩展，如果不及时发现和采取有效措施防治，则极易出现各类安全事故，如构件断裂、结构倒塌、设备失效、容器爆炸等。因此，裂纹损伤作为影响结构、设备安全事故的主要原因之一，在工程领域已受到普遍关注和重视，含裂纹结构、设备的振动分析、裂纹识别等问题已成为学者研究的热点问题之一，Dimarogonas［1］和 Papadopoulos［2］对该领域的研究进展进行了详细的综述。

线性断裂力学理论的重大突破归功于Irwin应力场强度因子概念的提出［3］。Irwin通过把裂纹尖端局部的宏观力学行为与微观特征联系起来，确定了裂纹尖端前缘区域的应力和位移场与每种裂纹类型的关系。此后，Dimarogonas和 Papadopoulos［4－7］依据线性断裂力学理论，计算了各种荷载作用下由裂纹引入的局部柔度系数，建立了以“有限元”或“弹簧铰”刻画裂纹局部行为的裂纹模型。他们开创性的工作推动了含裂纹结构的动力学发展。基于局部柔度的裂纹模型具有明确的物理意义、理论性强、应用性好等优点，被广泛应用于裂纹转子和裂纹梁的动力学分析。

然而，令人遗憾的是目前基于局部柔度建立的裂纹模型存在以下不足:① 多数裂纹模型是针对矩形或圆形截面的实体结构建立的，如矩阵或圆形截面的梁、杆类结构，而针对管道结构的裂纹模型只有少数文献报道［8－10］;② 大多数裂纹模型存在同样的假设，即裂纹尖端方向与外力方向垂直或平行。但是，在实际工程中，裂纹结构的裂纹尖端方向并不局限于与外力垂直或平行，还存在与外力成任意角情况［11－12］。在裂纹转子动力学中裂纹与外力成任意角的裂纹模型已有研究工作涉及，但是对于管道裂纹与外力成任意角的裂纹模型研究却鲜有报道。Naniwadekar等人［10］利用试验研究了裂纹与外力成任意角的管类结构的振动特性，但文中并没有给出裂纹与外力成任意角的管道局部柔度的解析表达式，因而，文中结果很难应用于工程实际。

为了研究含裂纹管道的力学行为，发展合适的裂纹模型必不可少。而推导合理的裂纹局部柔度系数广义解是建立管类结构裂纹模型的关键环节。本文开展了裂纹与外力成任意角的管道局部柔度的理论研究，推导了含有非贯穿直裂纹管道在轴力、剪力和弯矩作用下的局部柔度方程的广义解，并进行求解和验证，进一步发展和完善了裂纹结构的局部柔度求解理论。

1 局部柔度系数方程的理论推导

非贯穿直裂纹如图1所示，裂纹深度为a，管壁厚为t，管外径为De，管内径为Di。裂纹管单元受到轴力P1、剪力P2和弯矩P3的联合作用。假设P1方向与管轴重合;P2、P3方向如图1(a)所示，与裂纹截面的法线n成φ角度，本文称φ为方向角。根据Dimarogonas建立裂纹转轴局部柔度的思想，把裂纹区域离散为一序列独立的矩形条带，各矩形条带按照裂纹梁理论计算附加应变能，然后积分得到总应变能，从而求得裂纹引入的局部柔度［1，2］。

根据图1(b)所示的几何关系，得到如下的表达式:

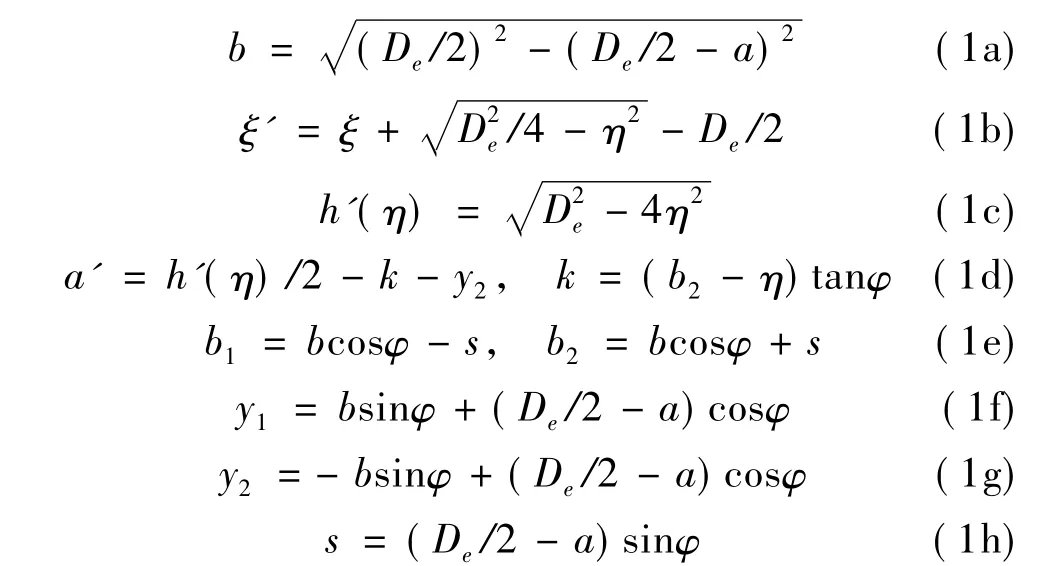
式中:2b为裂纹尖端处宽度;ξ'为距离积分条带顶部的局部深度变量;h'(η)为积分条带深度，ξ、η分别为全局坐标下的深度变量和偏移距离。

假设在外力作用下，结构中裂纹区域处于弹性阶段，根据线弹性断裂力学理论，裂纹出现所产生的附加应变能［6］表示为:

式中:J为应变能释放率，Ac为有效裂纹面积。裂纹引起的附加应变能释放率J可表示为:

式中:KI1、KI2、KI3分别为轴力、剪力、弯矩引起的 I型裂纹的应力强度因子;KII2为剪力引起的II型裂纹的应力强度因子。在平面应力状态下 E'=E;在平面应变状态下E'=E/(1－ν2)。其中，E为弹性模量，ν为泊松比。

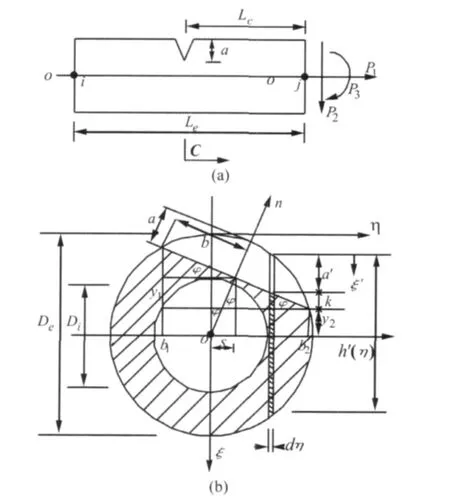
图1 (a)裂纹管单元;(b)裂纹截面几何尺寸Fig.1(a)Cracked pipe element;(b)Cracked section geometry

对于含裂纹管道，在轴力、剪力和弯矩作用下，各条带裂纹区域应力强度因子可表示为［10］:

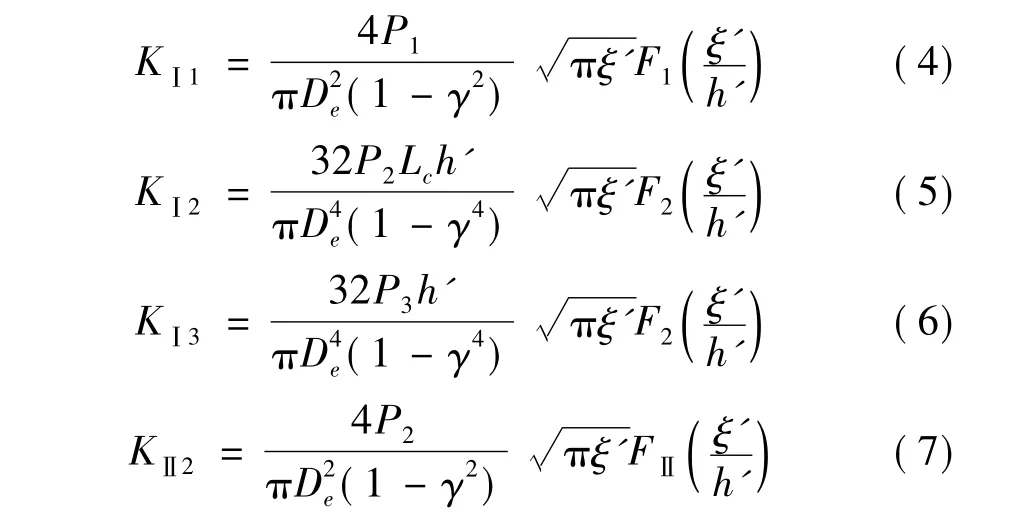
式中:Pi(i=1，2，3)分别表示裂纹单元的轴力、剪力和弯矩，γ=Di/De，F1、F2、FⅡ为应力强度因子的修正系数，可表示为［11，13］:

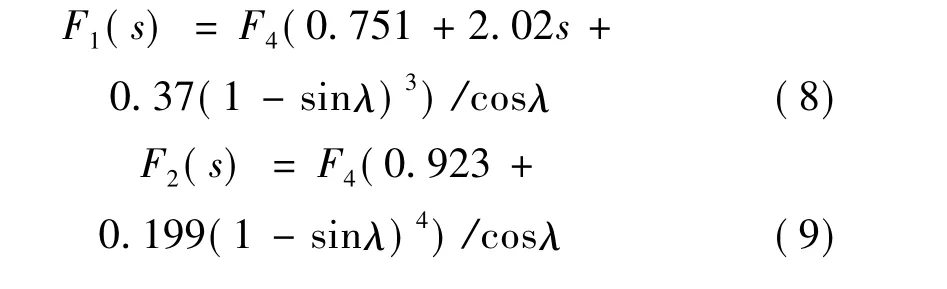
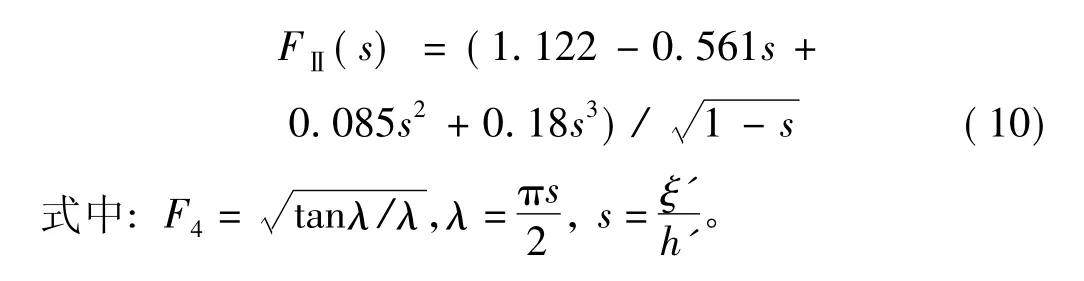
根据卡式定理(Castigliano’s theorem)，裂纹引入的附加位移可表示为应变能对力的导数:

则裂纹引起的附加局部柔度可表示为:

式中:cij(i，j=1，2，3)为各荷载引入的含裂纹管道的局部柔度系数。

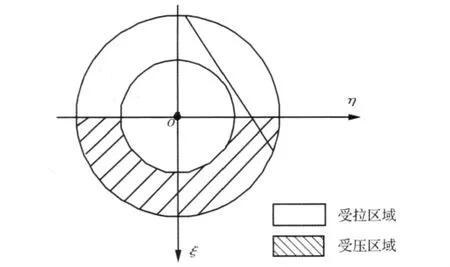
图2 φ与裂纹受拉区域的关系Fig.2.The relationship between angle φ and tension area

对于图2所示的含裂纹管道，受到垂直面内的弯矩P3作用时，裂纹截面一部分处于受拉区域，另一部分处于受压区域。若裂纹尖端处于拉伸状态，则裂纹表面是张开的，导致了含裂纹管道弯曲刚度的降低;若裂纹尖端处于受压状态，则裂纹处于闭合状态，此时可认为含裂纹管道弯矩刚度与完好状态相等。可以看出，含裂纹管道在弯矩作用下的局部柔度系数与裂纹方向角φ密切相关。由于裂纹引起的局部柔度是方向角φ的周期性函数，因此，裂纹的张开—闭合行为随着方向角的大小而改变。随着φ的变化，裂纹截面会出现以下三种状态:① 完全张开状态;② 部分张开—部分闭合状态;③ 完全闭合状态。

已有研究证明，只有受拉区的张开裂纹对结构局部柔度产生影响，而受压区的闭合裂纹对结构局部柔度的影响可忽略不计［11－12］。然而，裂纹截面在剪切应力和轴向应力作用下，局部柔度系数的求解不受裂纹拉压状态的影响，需要计算整个裂纹表面区域应变能的贡献。

转换积分表示方式，令 x=ξ/De，y= η/De，则 dξ'=Dedx，dη =Dedy，有:

把式(3)～式(7)代入式(12)，然后转换积分表达方式，可推导出各荷载引起的局部柔度系数cij，为了直观比较各局部柔度系数cij，对局部柔度系数进行了无量纲处理，得到含裂纹管道无量纲的局部柔度系数AF(i，j)(本文简称“无量纲柔度”)。任意方向角φ条件下推导的管道无量纲柔度表达式与φ=0时明显不同，任意方向角φ含裂纹管道的无量纲柔度不仅是裂纹深度的函数，同时也是裂纹方向角φ的函数。推导的无量纲柔度方程如下:

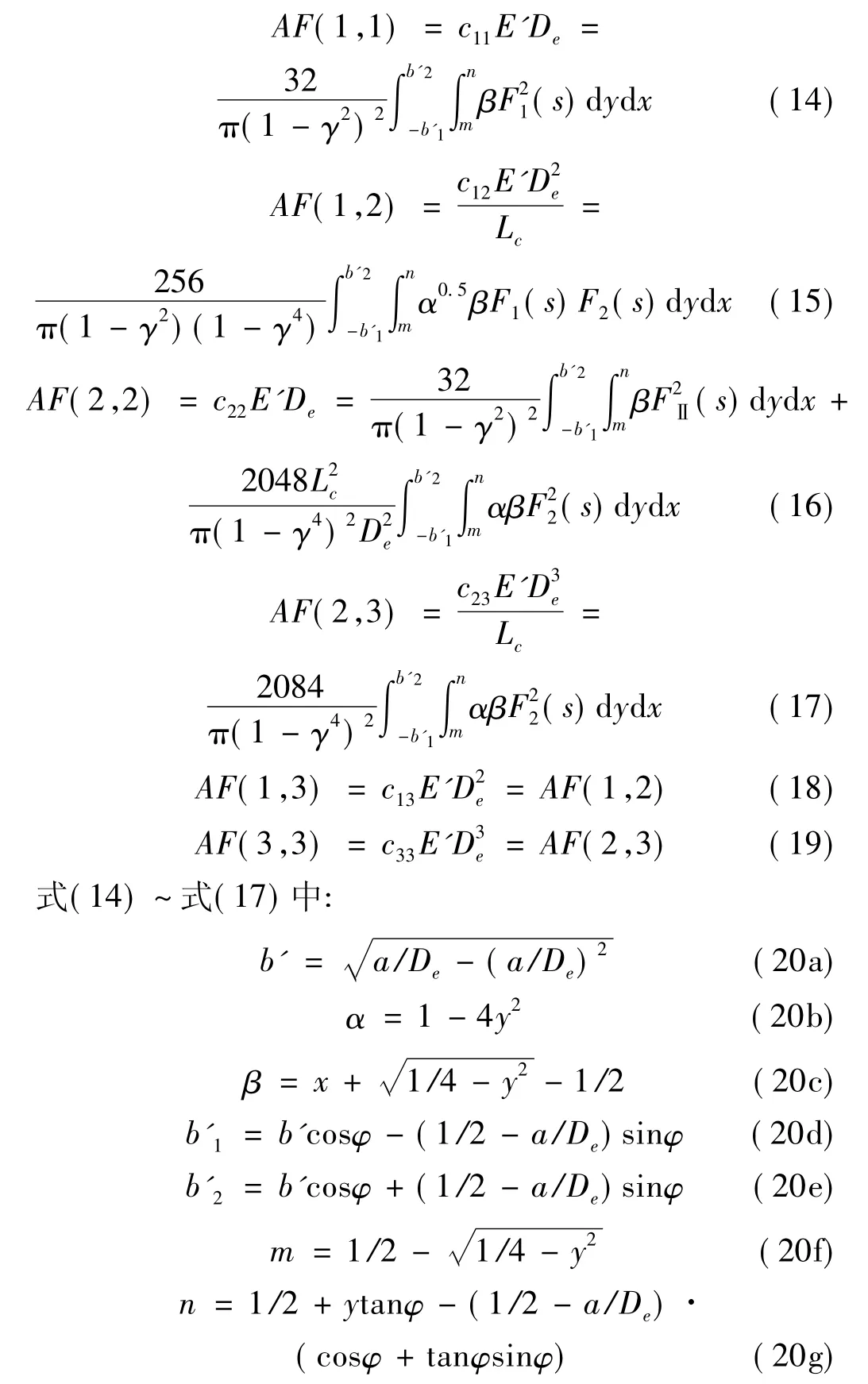
Chasalevris 和 Papadopoulos［11］研究含裂纹转轴局部柔度时指出:对于任意方向角φ的转轴，由于应力强度因子应用条件的限制，方向角φ介于±30°之间时，进行弯矩作用下无量纲柔度求解的精度较高。随着方向角φ的改变，裂纹截面的有效积分面积也将随之变化。当φ≥φcr(φcr为临界角)时，裂纹部分截面开始进入受压区，裂纹截面的有效面积逐渐减小;当φ≥φcl(φcl为闭合角)时，裂纹完全位于受压区，裂纹闭合，此时弯矩引起的AF(3，3)=0。

图3 (a)水平面内的弯矩作用;(b)垂直面内的弯矩作用Fig.3(a)bending in horizontal plane;(b)bending in vertical plane

对于裂纹深度为 a的管道，由 y1、y2可求得 φcr、φcl值。

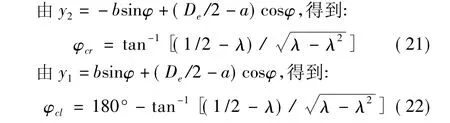
式中，λ=a/De。可以看出临界角φcr、闭合角φcl均是裂纹相对深度的函数。对于给定裂纹深度的管道，管道受到垂直面内的弯矩(φ=90°)与管道受到水平面内的弯矩(φ=0°)引起的局部柔度相同。因此，在垂直面内的弯矩作用下，当方向角φ满足60°≤φ≤90°时，根据上述思想推导的无量纲柔度方程为

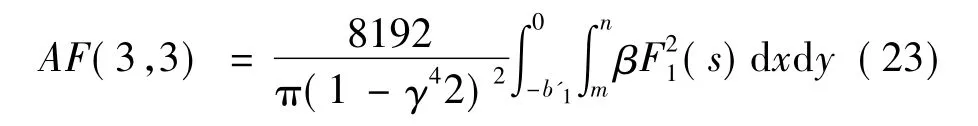
与式(17)类似，利用式(23)进行水平面内弯矩作用下无量纲柔度计算时，要求－30°≤φ≤0°，即等价于垂直面内弯矩作用下60°≤φ≤90°的条件。所以，在0°≤φ≤180°的范围内，局部柔度AF(3，3)的计算分3部分进行，即0°≤φ≤30°、60°≤φ≤90°、φcl≤φ≤180°。另外，由于满足可导性和连续性的边界条件，30°≤φ≤60°和90°≤φ≤φcl的局部柔度系数可通过B样条曲线插值得到［11］。至此，当方向角φ为任意值时，含非贯穿直裂纹管道的无量纲柔度AF(3，3)均可通过计算得到。

2 无量纲柔度的求解与验证

式(14)～式(19)是关于 x、y内积分限为函数的双重积分，且内部积分函数表达式十分复杂，无法通过直接积分给出无量纲柔度方程的解析表达式。因此，本文采用数值积分方法求解局部柔度系数。根据文献［14］中给出的适应性Simpson积分算法的思想和建议，本文应用Matlab软件编写了无量纲柔度方程求解的数值积分算法程序(Local Flexibility Integral Program-LFIP)，计算流程如图4所示。对于已知物理参数和截面尺寸的管道，根据LFIP可以计算任意深度a、任意方向角φ含非贯穿直裂纹管道的无量纲柔度系数。

图4 无量纲柔度的求解流程图Fig.4.Flow chart of the nondimensional flexibility

对于含任意方向角φ非贯穿直裂纹的管道，由上述内容可知，相对轴力、剪力荷载，弯矩作用引起的无量纲柔度AF(3，3)的计算较为复杂，计算过程中涉及裂纹表面拉压区域面积的判断以及利用B样条插值求解其余方向角φ的AF(3，3)值。限于篇幅，本文则重点讨论任意方向角φ管道的无量纲柔度 AF(3，3)特点。假定 γ =0.5，选取三组 φ1、φ2、φ3共 12 个不同的角度进行计算，如表1所示。首先根据式(21)、式(22)计算a/De取不同值时的临界角φcr与闭合角φcl，结果如表2所示。

表1 方向角φ取值Tab.1 Values of the angle φ

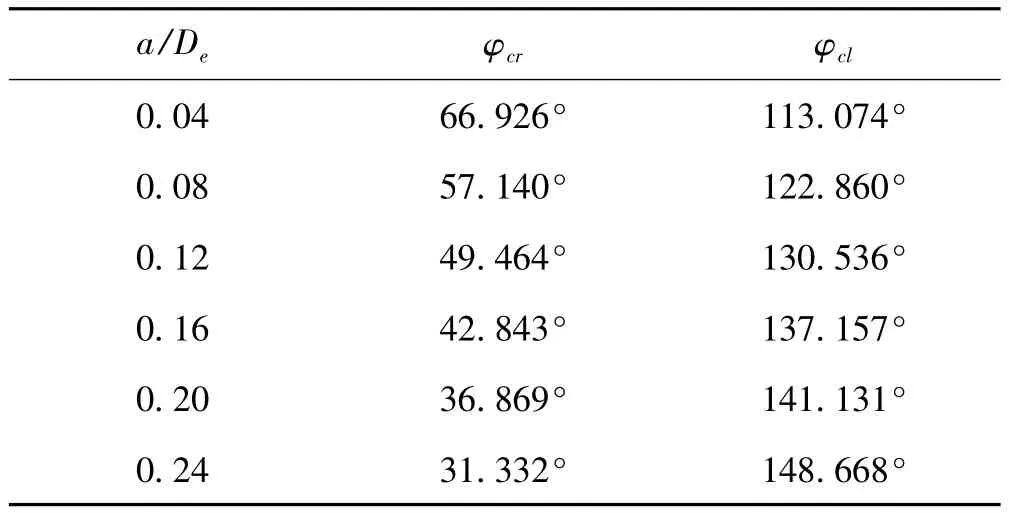
表2 各裂纹深度对应的φcr和φcl值Tab.2 Values of φcrand φclwithin different crack depth

根据表2的计算结果可知，φ3＞φcr时裂纹完全位于受压区，即裂纹完全闭合，无量纲柔度系数AF(3，3);φ1＜φcr时裂纹完全位于受拉区，裂纹张开;φ2＞φcr时裂纹部分位于受压区，部分位于受压区，本文主要讨论 φ1、φ2两组管道的无量纲柔度 AF(3，3)，其余方向角φ的AF(3，3)可通过B样条曲线插值获得。用本文方法求解得到AF(3，3)结果如图5所示。

从图5可以看出:① 在裂纹角φ相同情况下，随着裂纹深度的增加，AF值随之增大;② 在裂纹深度相同条件下，随着方向角φ的增加，AF值随之减小;③根据B样条曲线插值可求得其余方向角φ时的AF(3，3)值。

Naniwadekar［10］等人利用试验研究了含裂纹钢制管道因裂纹出现而引入的附加等效刚度。为了验证本文得到的含任意方向角非贯穿直裂纹管道局部柔度系数的正确性，选取Naniwadekar等人的试验管道模型作为基准模型。Naniwadekar等人在试验中使用线切割制作裂纹，当方向角φ＞φcr(即一部分裂纹进入受压区)时，因为线切割裂纹存在2 mm切口宽度，试验中进入受压区的裂纹表面并不会闭合，这与真实裂纹是有所区别的。因此，Naniwadekar等人试验中 φ 为0°、10°、20°、30°的结果与本文具有可比性。模型物理参数为:外径 De为0.037 8 m，内径 Di为 0.027 8 m，密度 ρ为7 860 kg/m3，弹性模量E为173.8 GPa;相对裂纹深度a/t分别取 0.2、0.4、0.6、0.8;方向角 φ 分别取:0°、10°、20°、30°。

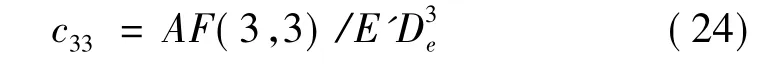
由式(19)，得到弯矩作用下的局部柔度系数c33:根据本文方法计算得到φ为0°、30°时局部柔度系数c33值，与 Naniwadekar等人的试验结果对比如图 6所示。

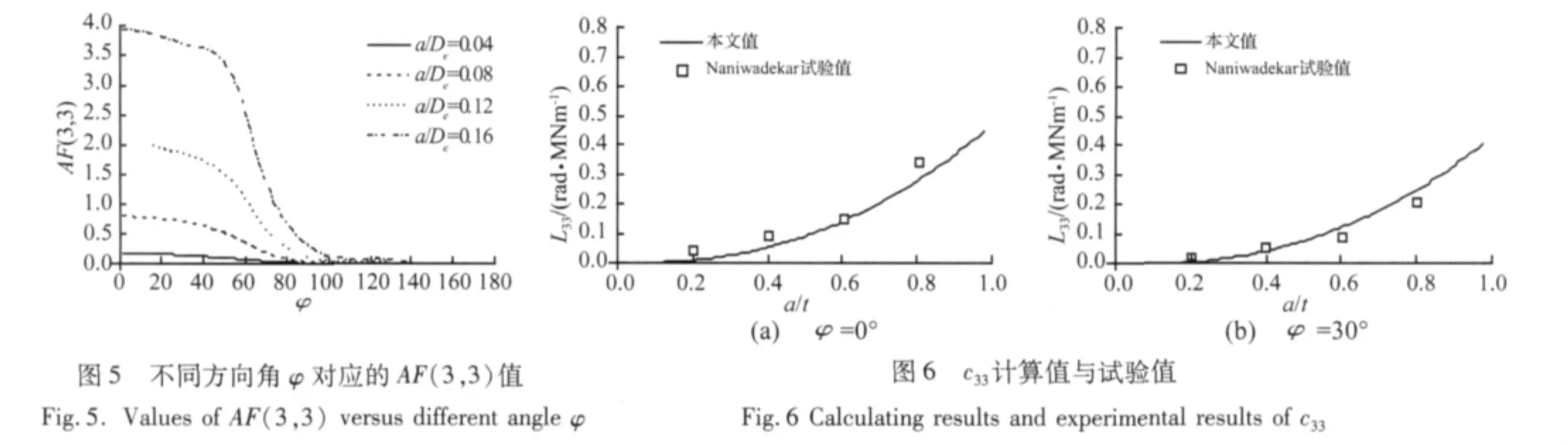
从图6可以看出，使用本文理论求解的局部柔度系数与试验结果基本吻合，误差较小。误差的主要来源:① 理论与试验中的裂纹形式。Naniwadekar等人在试验中使用线切割制作裂纹，虽然裂纹切口较小，但与实际裂纹还是存在差异，真实裂纹与线切割裂纹的应力场分布特点不同。② 理论计算中存在近似成分。管道裂纹截面并非完全的平面应变或平面应力，计算中E'取值对计算结果有影响。另外，利用离散的矩形条带进行积分求解也存在近似成分。相对于文献［10］，本文避免了获得局部柔度系数所进行的大量试验工作，求解结果满足实际要求，便于工程应用。总而言之，本文方法满足含任意方向角，且直裂纹深度a＜t管道的局部柔度系数求解，为含裂纹管道的振动分析和裂纹识别提供了模型参数保障，完善了现有工作的缺失和不足。

3 结论

本文利用线性断裂力学理论中的应变能释放率原理，推导了含任意方向角非贯穿直裂纹在轴力、剪力和弯矩作用下的局部柔度系数方程，考虑了裂纹表面拉压区域变化对局部柔度系数的贡献，采用适应性Simpson数值积分算法编写了局部柔度系数计算程序，并给出了方向角φ=0°～180°范围内局部柔度系数的计算原则:在0°≤φ≤180°范围内，弯矩引起的局部柔度系数分为0°≤φ≤30°、60°≤φ≤90°、φcl≤φ≤180°计算。30°≤φ≤60°和90°≤φ≤φcl的局部柔度系数通过 B 样条曲线插值得到。

利用Naniwadeker等人的试验结果作为基准，对本文推导的含任意方向角裂纹管道局部柔度系数进行验证。结果表明，本文计算值与Naniwadeker等人试验值基本吻合，从而验证了本文局部柔度系数推导和求解的正确性。本文发展的含任意方向角非贯穿直裂纹管道的局部柔度求解方法具有理论性强、应用范围广、具有实际工程应用价值。本文研究结果为含裂纹管道的力学分析、裂纹识别提供了基础和参考。

［1］Dimarogonas A D.Vibration of cracked structure:a state of the art review［J］.Engineering Fracture Mechanics，1996，55(5):831－857.

［2］Papadopoulos C A.The strain energy release approach for modeling cracks in rotors:A state of the art review［J］.Mechanical Systems and Signal Processing，2008，22(4):763－789.

［3］Irwin G R.Analysis of stresses and strains near the end of a crack traversing a plate ［J］.Journal of Applied Mechanics，1957，24:361－364.

［4］Zou J，Chen J，Niu J C，Geng Z M.Discussion on the local flexibility due to the crack in a cracked rotor system ［J］.Journal of Sound and Vibration，2003，262(2):365－369.

［5］Papadopoulos C A.Some comments on the calculation of the local flexibility of cracked shafts［J］.Journal of Sound and Vibration，2004，278(4－5):1205－1211.

［6］Zheng D Y，Kessissoglou N J.Free vibration analysis of a cracked beam by finite element method［J］.Journal of Sound and Vibration，2004，273(3):457－475.

［7］ Dong G M，Chen J，Zou J.Parameter identification of a rotor with an open crack.European JournalofMechanics A/Solids，2004，23(2):325－333.

［8］Liu D，Gurgenci H，Veidt M.Crack detection in hollow section structures through the coupled response measurements［J］.Journal of Sound and Vibration，2003，261(1):17－29.

［9］ Zheng D Y，Fan S.Vibration and stability of cracked hollowsectional beams［J］.Journal of Sound and Vibration，2003，267(4):933－954.

［10］ Naniwadekar M R，Naik S S，Maiti S K.On predection of crack in different orientations in pipe using frequency based approach［J］.Mechanical Systems and Signal Processing，2008，22(3):693－708.

［11］ Chasalevris A C， Papadopoulos C A. Identification of multiple cracks in beams under bending［J］.Mechanical Systems and Signal Processing，2006，20(7):1631－1673.

［12］Chasalevris A C，Papadopoulos C A.Coupled horizontal and vertical bending vibrations of a stationary shaft with two cracks［J］.Journal of Sound and Vibration，2008，309(3 －5):507－528.

［13］Tada H，Paris P C，Irwin G R，The stress analysis of cracks handbooks(ThirdEdition)［M］.New York:ASME Press，2000.

［14］ Gander W，Gautschi W.Adaptive quadrature-revisited［J］.BIT，2000，40(1):84－101.

General solution to local flexibility of a pipe with a part-through straight crack

HU Jia-shun1，SUN Wen-yong1，LIU Duo2，ZHOU Jing2

(1.Research Department of Safety Technology，CNPC Research Institute of Safety＆ Environment Technology，Beijing 100083，China;2.State key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 110624，China)

The crack model based on local flexibility has

attractive attentions in engineering.However，the theoretical studies on local flexibility of a pipe with a crack with an arbitrary direction are less conce rned.The local flexibility equations of a pipe with a part-through crack subjected to axial force，shear force and bending moment were deduced using theories of linear fracture mechanics and taking into the effect of the direction angle of the crack on the local flexibility of the pipe into account.An adaptive Simpson method was used to obtain the flexibility coefficients of the cracked pipe and the results were compared with those of Naniwadekar's test to validate the proposed approach.The results demonstrated that the proposed approach is correct，it is suitable for vibration analysis of pipe-like structures with an arbitrary direction angle crack.

vibration analysis;local flexibility;pipe;crack;direction angle of crack

O346

A

中国石油安全环保技术研究院基金(D－03－2010－2－021);国家自然科学基金重点项目(50439010)

2010－01－28 修改稿收到日期:2010－04－12

胡家顺 男，博士，1981年生