含圆周非贯穿裂纹悬臂管道的振动分析与裂纹识别
2011-01-25胡家顺孙文勇
胡家顺,孙文勇,周 晶
(1.中国石油集团安全环保技术研究院安全技术研究所,北京 100083;2.大连理工大学 海岸和近海工程国家重点试验室,大连 116024)
含圆周非贯穿裂纹悬臂管道的振动分析与裂纹识别
胡家顺1,孙文勇1,周 晶2
(1.中国石油集团安全环保技术研究院安全技术研究所,北京 100083;2.大连理工大学 海岸和近海工程国家重点试验室,大连 116024)
根据线性断裂力学理论和应变能释放原理,推导了含圆周非贯穿裂纹管道在轴力、剪力和弯矩等荷载作用下的局部柔度系数方程,利用适应性Simpson方法编写了数值积分程序进行局部柔度系数求解,建立了含裂纹管道的二维有限元模型进行含裂纹悬臂管道的振动特性分析,应用等值线图原理进行了悬臂管道的裂纹识别。研究结果表明:裂纹模型克服了当前裂纹模型仅针对特定的荷载模式或非空心截面的缺陷,基于等值线图法能有效识别含裂纹悬臂管道的裂纹位置、深度。
振动分析;裂纹识别;局部柔度;管道;裂纹
海洋结构如海底管道、海洋平台通常是由金属管道焊接而成,随着服役年限的增长,管道在静力和交变的动力荷载作用下将出现裂纹。结构的初始裂纹是不易被发现的,但裂纹扩展往往导致重大灾难性事故的发生,如管道断裂、平台倒塌。裂纹的存在某种程度上决定着结构的安全性,而安全性是工程结构最基本的要求。因此,含裂纹管道的力学分析和裂纹识别应受到足够重视。
荷载作用下,结构中裂纹尖端附近区域出现应变能集中,引起了结构局部柔度的变化。早期,Irwin提出了局部柔度的概念从宏观上量化荷载与裂纹尖端应力集中的关系[1]。Dimarogonas[2]用无质量转动弹簧模拟裂纹,依据断裂力学原理计算弹簧的等效刚度,建立了基于局部柔度的Euler-Bernoulli裂纹梁模型。此后,Papadopoulos和 Dimarogonas[3-5]提出了完整的 6 ×6 局部裂纹柔度阵求解理论,该理论不仅适合Euler-Bernoulli裂纹梁,也适用于任意荷载条件下Timoshenko裂纹梁的力学分析[6]。上述基于局部柔度建立的裂纹模型是以含裂纹的矩形、圆形实心结构为研究对象,不适合含裂纹管道的力学分析。然而,目前基于局部柔度的管道裂纹模型、裂纹识别只有少量文献报道[7-9]。
本文根据线性断裂力学理论,推导了含圆周方向外表面非贯穿裂纹(以下简称“圆周非贯穿裂纹”)管道在轴力、剪力和弯矩作用下的局部柔度方程,采用适应性Simpson数值积分计算得到相应的局部柔度系数,在此基础上建立了含裂纹管道的二维有限元模型。基于建立的含裂纹管道有限元模型,进行了含裂纹悬臂管道的振动分析,并应用等值线图法进行了裂纹位置、深度的识别。本文将管道视为梁-杆模型,避免了建立三维壳模型进行理论分析的难度,同时又有较高的精确度,可以满足工程需要。
1 局部柔度方程的理论推导
圆周非贯穿裂纹是管道的一种典型裂纹形式。本文研究的圆周非贯穿裂纹如图1(b)所示,环形方向裂纹深度为 ,管壁厚为 ,管外径为 ,管内径为 。假设轴力方向与管轴重合;剪力和弯矩方向如图1(a)所示,位于平面内。与梁类结构裂纹不同,管类结构圆周非贯穿裂纹区域是一个环形区域,无法直接获得其应力强度因子求解其局部柔度系数。根据Dimarogonas[2]建立裂纹转轴局部柔度的思想,把裂纹区域离散为一序列近似于梯形的微小条带,如图1(b)所示。各个条带裂纹区域按照平面裂纹梁理论求解其附加应变能,把各个条带的应变能进行累加得到裂纹引入的总应变能,然后对各荷载进行求导即可获得含圆周非贯穿裂纹管道的局部柔度系数。
假设外力作用下,结构中裂纹区域处于弹性阶段,根据线弹性断裂力学理论,裂纹出现所产生的附加应变能[2]表示为:

式中,J为应变能释放率,Ac为有效裂纹面积。裂纹引起的附加应变能释放率可表示为:
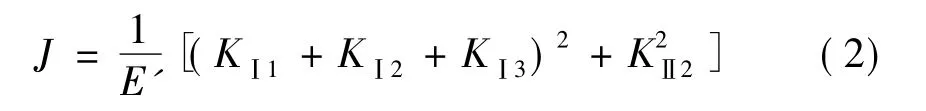
式中,KⅠ1、KⅠ2、KⅠ3分别为轴力、剪力、弯矩引起的Ⅰ型裂纹的应力强度因子;KⅡ2为剪力引起的Ⅱ型裂纹的应力强度因子。在平面应力状态下E'=E;在平面应变状态下E'=E/(1-υ2)。其中:E为弹性模量,υ为泊松比。
根据卡氏定理,裂纹引入的附加位移ui表示为:
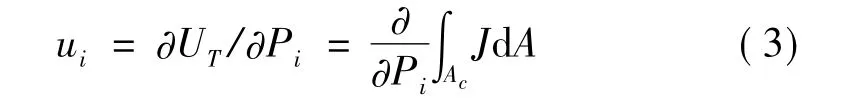
式中,Pi(i=1,2,3)分别对应裂纹单元的轴力、剪力和弯矩。则裂纹引起的局部柔度系数可表示为:
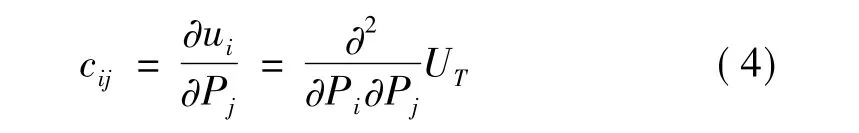
式中,cij为裂纹引入的局部柔度系数。
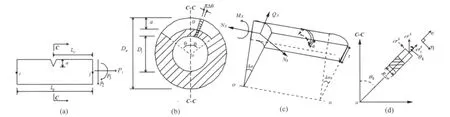
图1 (a)裂纹管单元;(b)圆周非贯穿裂纹截面几何尺寸;(c)裂纹微元体;(d)微元体应力分解Fig.1(a)Cracked pipe element.(b)A circumferential part-through crack section geometry.(c)The strip of crack section.(d)The stress decomposition of the strip.
对于图1(b)所示的圆周非贯穿裂纹截面,可以把裂纹截面部分等分成2n个微元体,每个微元体的圆心角为Δθ=θ/n,如图1(c)所示。如果每个微元体的宽度足够小,环形的微元体截面可以等效为梯形截面,为了方便积分求解每个微元体的附加应变能,进一步把等效梯形截面近似为同高且面积相等的矩形,宽度为RΔθ,其中R管道的平均半径,R=(Di+De)/4。每个微元体中裂纹引起的附加应变能表示为:

式中,UkT为第k个微元体裂纹引入的应变能,Jk为第k个微元体的应变能释放率。ε、η分别为微元体沿着圆心方向和垂直圆心方向的积分变量。
对于裂纹截面的第个微元体,考虑裂纹微元体在C-C轴上应力分量,如图1(d)所示,则在轴力、剪力和弯矩作用下的应力强度因子可表示[10]为:
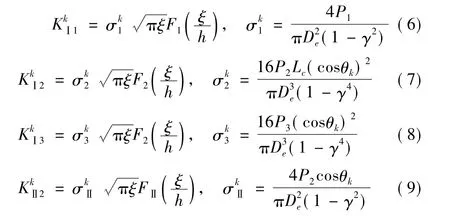
式中,γ=Di/De,θk为微元体中心线与C-C轴之间的夹角,如图1(d)所示,F1、F2、FⅡ为裂纹应力强度因子的修正系数[10],表达式如下:取微元体的宽度RΔθ无穷小,则含裂纹管道的总应变能可以表示为全部微元体应变能的积分格式:

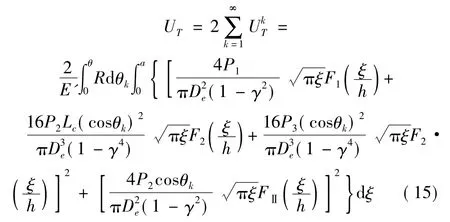
由式(4)和式(15)可求得含裂纹管道的局部柔度系数,表示为:


式(22)-式(27)是关于x、θ内积分限为函数的双重积分,且内部积分函数十分复杂,无法通过直接积分给出无量纲柔度方程的解析表达式。为了获得较为精确的局部柔度系数,本文采用适应性Simpson数值积分方法对柔度方程进行求解,适应性Simpson算法具有求解速度快,精度高等特性,详细算法可参考文献[11]。
2 含裂纹悬臂管道的振动分析
求得含裂纹管道的局部柔度系数后,可建立用扭转弹簧模拟的“弹簧铰模型”或用局部柔度矩阵构建的“有限元模型”。本文以含裂纹管道的有限元模型为技术手段,求解裂纹管道结构的动力特性。如图1(a)所示裂纹管单元的总体柔度等价于单元无裂纹时柔度与裂纹引起局部柔度的代数和[10]:含裂纹管道的动力特征方程表示为:

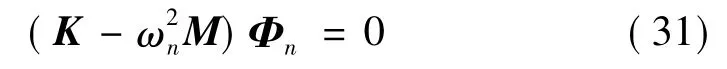
式中:K、M分别为含裂纹管道的总刚度矩阵和质量矩阵;ωn、Φn分别为固有圆频率和振型。
假设裂纹不引起结构质量矩阵的变化,则无裂纹管单元刚度矩阵和管单元一致质量矩阵分别表示为:

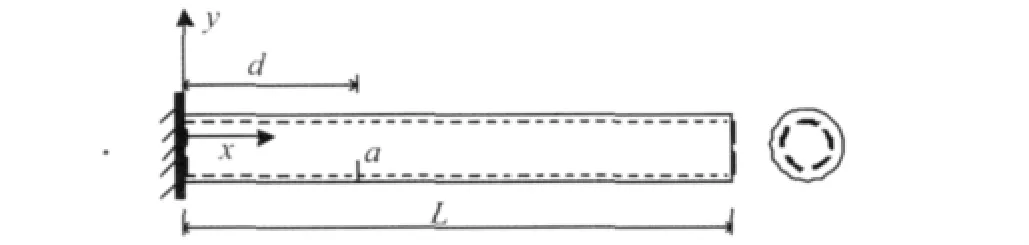
图2 含裂纹悬臂管道示意图Fig.2 Sketch of cracked pipe with cantilever constraints

表1 管道的物理参数和几何尺寸Tab.1 Physical parameters and geometrical sizes
含裂纹悬臂管道尺寸如图2所示,管道的物理参数和几何尺寸见表1。假设圆周非贯穿裂纹的圆心角θ为π/2,分析裂纹位置、裂纹深度变化条件下结构前三阶固有频率的变化规律。令fui(i=1,2,3)为无裂纹管道的固有频率计算值,fci(i=1,2,3)为含裂纹管道的固有频率计算值。定义无量纲参数固有频率变化率Fr:

图3-图5给出了含圆周非贯穿裂纹悬臂管道的前三阶固有频率随裂纹位置、深度的变化率,图中d/L、a/t分别为裂纹相对位置和相对深度。
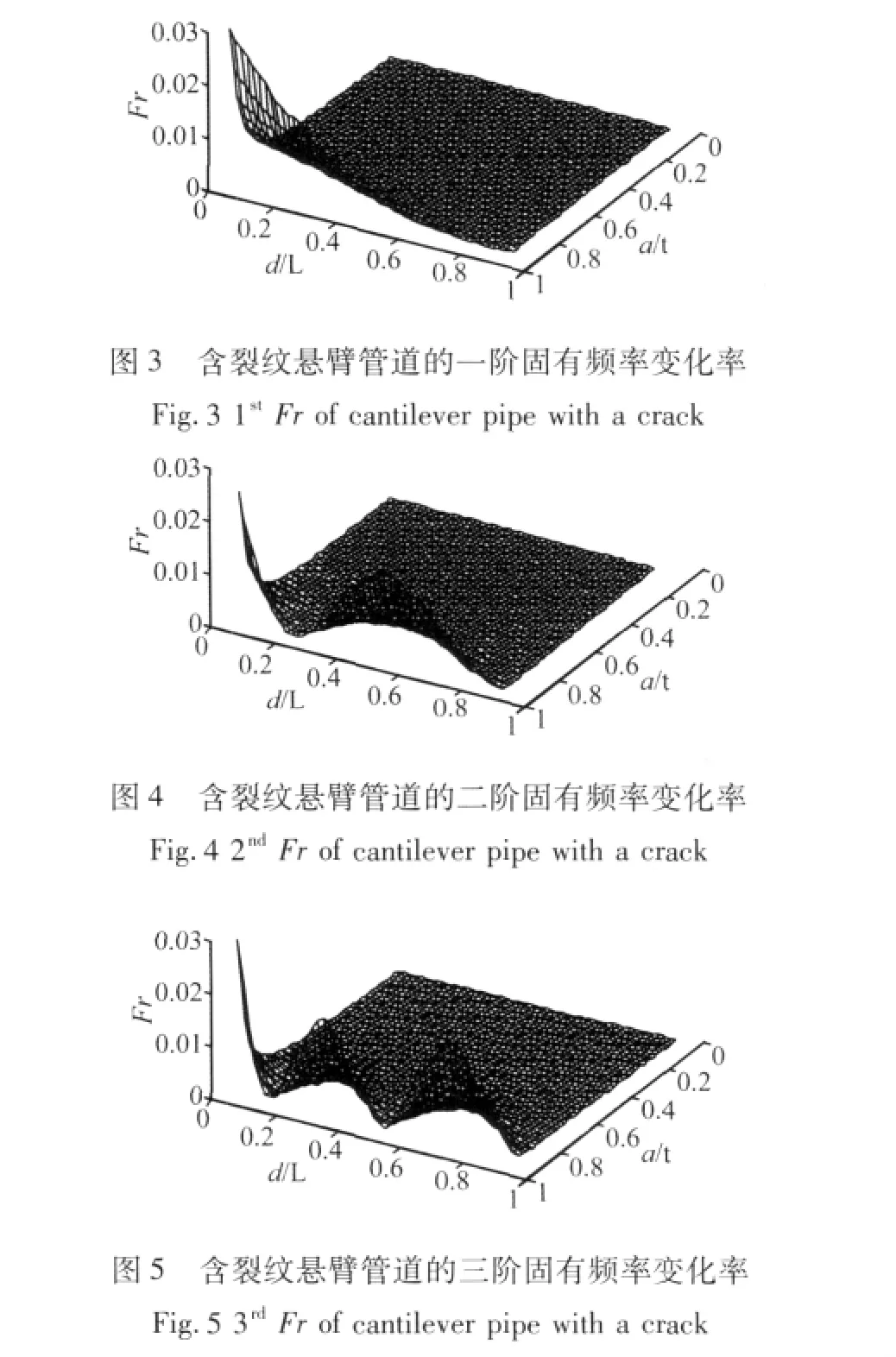
从图3-图5中可以看出:(1)对于悬臂管道,在裂纹位置相同条件下裂纹越深,其Fr值越大,固有频率降低越明显。(2)在裂纹深度相同条件下,不同裂纹位置、不同阶次固有频率的Fr值也不相同。结构一阶固有频率呈现单调变化,裂纹距离固定端越近,裂纹越深Fr值越大,反之越小;而结构二阶、三阶固有频率的Fr值并不随着裂纹位置的改变呈单调性变化,二阶固有频率Fr值出现两处局部最大值,三阶固有频率Fr值出现三处局部最大值。
3 含裂纹悬臂管道的裂纹识别
目前存在的基于固有频率的裂纹识别方法主要有:(1)频率变化(平方)比法[12],通常只能识别裂纹存在与裂纹位置。(2)等值线图法[13],根据裂纹深度和裂纹位置与各阶频率变化曲线之间的关系,寻找各曲线的交点坐标从而达到裂纹参数的识别目的,可确定裂纹深度、位置。优点在于测量系统存在一定误差情况下,仍然可以给出满足工程需要的识别结果,而且方法简单,容易应用于工程实践。(3)基于频率的参数反演方法[14],虽然具有较高的精度,但是在进行参数反演时无论应用何种优化算法其识别效率是很低的,往往因为反演响应曲面的复杂性和参数选择的不当出现误判。考虑到工程实用性,本文根据等值线图法的原理研究管道的裂纹识别问题。
基于裂纹位置与固有频率变化之间的关系,可绘制等值线图,基本步骤为:首先,计算无裂纹结构的固有频率,根据已知裂纹管固有频率计算前三阶固有频率变化率Fr;其次,寻找与上述前三阶固有频率变化率相等的裂纹位置和深度;最后,绘制前三阶固有频率变化率与裂纹位置和深度的等值线图,根据等值线图上交叉节点判别出裂纹位置和深度。
下面以含圆周非贯穿裂纹的悬臂管道为例,利用等值线图法进行裂纹识别研究。仍取表1中数据作为含裂纹管道的模型参数,由本文方法计算得到无裂纹悬臂管道的前三阶固有频率 fu1、fu2、fu3分别为62.28 Hz、390.3 Hz和 1 092.8 Hz。

图6 含裂纹悬臂管道的等值线图Fig.6 Contour diagram for cracked cantilever pipe
假设图2所示悬臂管道裂纹位置d/L为0.09,裂纹深度a/t为0.7,裂纹弧度θ/π恒为1/2。根据裂纹管有限元模型计算结构前三阶频率变化率分别为0.169%、0.068%和 0.017%,绘制的等值线图如图 6所示。图中前三阶频率变化率完全相交点的坐标为(a/t=0.69,d/L=0.89),裂纹位置和深度识别误差 ε为1%。可以看出,在裂纹弧度一定条件下,根据等值线图,能有效辨识悬臂管道中圆周非贯穿裂纹的位置和深度。
4 结论和展望
根据线性断裂力学理论和应变能释放原理,首次推导了含圆周非贯穿裂纹管道在轴力、剪力和弯矩作用下的局部柔度系数方程,并基于得到的局部柔度系数建立了含裂纹管道的有限元模型,进行了含裂纹管道的振动分析与裂纹识别。本文工作弥补了已有裂纹模型在含裂纹管道力学分析方面的不足。
本文将管道视为梁-杆模型,避免了建立三维壳体或三维实体有限元模型进行理论分析的难度,能够进行含裂纹管道的振动分析,计算速度快、精确度满足工程需要,本文建立的含裂纹管道二维有限元模型,为裂纹识别研究提供了模型基础,便于裂纹识别研究工作的开展。
研究结果表明,含裂纹管道的裂纹位置、裂纹深度明显影响结构的固有频率。根据完好管道、裂纹管道的前三阶固有频率,绘制固有频率变化率与裂纹位置、裂纹深度的等值线图,可以有效辨识悬臂管道中的裂纹位置、裂纹深度,识别精度较高。
[1]Irwin G R.Analysis of stresses and strains near the end of a crack traversing a plate[J].Journal of Applied Mechanics,1957,24:361-364.
[2]Dimarogonas A D.Analytical methods in rotor dynamics[M].Essex:Applied Science Publishers,1983.
[3]Papadopoulos C A.Some comments on the calculation of the local flexibility of cracked shafts[J].Journal of Sound and Vibration,2004,278(4-5):1205-1211.
[4]Papadopoulos C A.The strain energy release approach for modeling cracks in rotors:A state of the art review [J].Mechanical Systems and Signal Processing,2008,22(4):763-789.
[5]Dimarogonas A D.Vibration of cracked structure:a state of the art review[J].Engineering Fracture Mechanics,1996,55(5):831-857.
[6]胡家顺,冯 新,李 昕,等.裂纹梁振动分析和裂纹识别方法研究进展[J].振动与冲击,2007,26(11):146-152.
[7]Liu D,Gurgenci H,Veidt M.Crack detection in hollow section structures through the coupled response measurements [J].Journal of Sound and Vibration,2003,261(1):17-29.
[8]Naniwadekar M R,Naik S S,Maiti S K.On predection of crack in different orientations in pipe using frequency based approach[J].Mechanical Systems and Signal Processing,2008,22(3):693-708.
[9] Zheng D Y,Fan S.Vibration and stability of cracked hollowsectional beams[J].Journal of Sound and Vibration,2003,267(4):933-954.
[10] Zheng D Y,Kessissoglou N J.Free vibration analysis of a cracked beam by finite element method[J].Journal of Sound and Vibration,2004,273(3):457-475.
[11] Gander W,Gautschi W.Adaptive quadrature-revisited[J].BIT,2000,40:84-101.
[12] Cawley P,Adams R.The locations of defects in structures from measurements of natural frequencies[J].Journal of strain analysis,1979,14(2):49-57.
[13] Nikolakopoulos P G,Katsareas D E,Papadopoulos C A.Crack identification in frame structures[J].Computers and Structures,1997,64(1-4):389-406.
[14] Suh M W,Shim M B,Kim M Y.Crack identification using hybrid Neuro-genetic technique[J].Journal of Sound and Vibration,2000,238(4):617-635.
Vibration analysis and crack identification of a
cantilever pipe with a circumferential part-through crack
HU Jia-shun1,SUN Wen-yong1,ZHOU Jing2
(1.Research Department of Safety Technology,CNPC Research Institute of Safety& Environment Technology,Beijing,100083,China;2.State key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 110624,China)
The local flexibility coefficient equations of a pipe with a circumferential part-through crack subjected to axial force,shearing force and bending moment were derived by using theories of linear fracture mechanics and strain energy release principle.An adaptive Simpson quadrature method was used to conduct numerical integrations to obtain the flexibility coefficients.A finite element model was established to conduct the vibration analysis of a cracked cantilever pipe.In addition,the crack identifiation for the cracked cantilever pipe was investigated based on contour plots of frequency ratio as a function of crack location and crack depth.The results showed that the proposed model overcomes the shortcoming that the existing crack models are suitable only for calculating special loads or structures with non-hollow cross-section,and the contour diagram can identify crack location and depth effectively.
vibration analysis;crack identification;local flexibility;pipe;crack
O346
A
中国石油安全环保技术研究院基金(D-03-2010-2-021);国家自然科学基金重点项目(50439010)
2010-01-18 修改稿收到日期:2010-02-22
胡家顺 男,博士,1981年生
