一种非负矩阵分解的快速稀疏算法

宋金歌，杨 景，陈 平，佘玉梅

(云南民族大学数学与计算机科学学院，云南昆明650031)

1999年，Lee和Seung［1］首次提出了非负矩阵分解，为人们处理大规模数据提供了一种新的方法．2001年，Lee和Seung［2］给出了非负矩阵分解的乘性迭代公式，有效地保持了数据的非负性．由于非负矩阵分解算法易于实现，存储空间小，分解形式的可解释性好，所以被应用于文本分析与聚类、数字水印、人脸识别、图像检索、基因特征提取等研究中［3］．目前，人们对于非负矩阵的研究主要集中在3个方面：稀疏性增强的NMF算法;鉴别性NMF算法;加权NMF算法．

本文提出了一种非负矩阵分解的快速稀疏算法，通过代数变换把对原矩阵分解转化成对维数较低的对角矩阵的分解，在分解的过程中加入了对系数矩阵稀疏度的控制．给出了此算法的迭代规则以及收敛性证明过程，将其应用在文本文摘中．

1 非负矩阵分解问题

1.1 问题描述

给定一个n×m阶非负矩阵V，找到2个n×r和r×m阶的非负矩阵因子W和H，使得V=WH．将矩阵W称为基矩阵，矩阵H称为系数矩阵．

1.2 算法步骤

非负矩阵的分解是一种低秩逼近算法，常用V和WH间的欧几里德距离平方作为目标函数来达到最佳逼近．目标函数为：

NMF的实现是一个最优化问题，就是在约束条件W，H≥0下，寻找矩阵W和矩阵H，使得(1)式达到最小值，只有当V=WH的时候，(1)式才能取到最小值0．Lee等［2］利用梯度下降法给出一种乘法更新规则，迭代求得矩阵W和矩阵H．其算法如下：

Step1：对非负矩阵W和H随机赋初值;

Step2：更新W和H，更新规则为

Step3：重复Step2直至收敛．

2 非负矩阵分解的快速稀疏算法

2.1 基本思想

对于非负矩阵的分解问题，王文俊等［4］曾提出一种快速方法，在V=WH的两边左乘VT得：

令VTV=X，VTW=Y，则(3)式可变形为

由于(1)式和(4)式都含有权重系数矩阵H，所以可以把对矩阵V的分解转化为对矩阵X的分解，同样可以得到矩阵H．矩阵V是n×m阶的，而矩阵X是m×m阶的，对于高维小样本数据来说n＞＞m，所以此转化在矩阵分解过程中起到了降维的作用，使矩阵分解的复杂度降低．

对于非负矩阵稀疏度的约束，Hoyer［5］提出：约束矩阵W的稀疏度好，还是约束矩阵H的稀疏度好，还是约束两者的稀疏度好，取决于问题中特定的应用情况．比如，一个医生分析疾病模式，假设大部分疾病是稀有的(因此稀疏)．但是每种疾病都能引起大量的症状．假设矩阵的行代表症状，列代表不同的个体，这种情况下系数矩阵应该稀疏而基矩阵可以不受约束．另如，当需要学习图像数据库中有用的特征时，可能需要约束W和H的稀疏性才更有意义．这表明任何给定的对象是在当前的几张图像中并影响一少部分的图像．

对于处理行表示特征词，列表示句子的文本矩阵的分解来讲，采用约束矩阵H的稀疏度．所以在对上述对角矩阵X分解时，在目标函数中采用了1－范数形式来约束矩阵H的稀疏度．目标函数为：

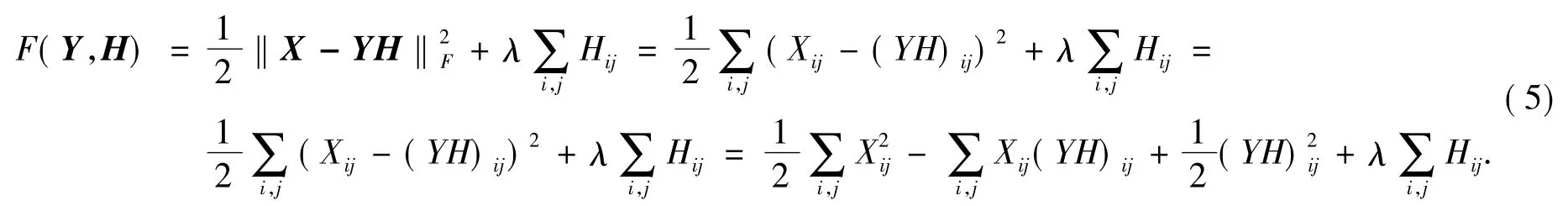
这样可以使矩阵分解的结果得到较高的稀疏性，合适的稀疏性在保留数据的主要特征的基础上，还可以减少储存空间，提高运算效率，有利于快速处理大规模数据．

在X=YH的分解过程中，求得全局最优解比较困难，因为(5)式对Y和H来讲是非凸的．但是可以将数值优化中的负梯度下降法和迭代规则应用于局部最优解中．

首先，在非负条件下初始化Y0和H0．通过迭代公式：

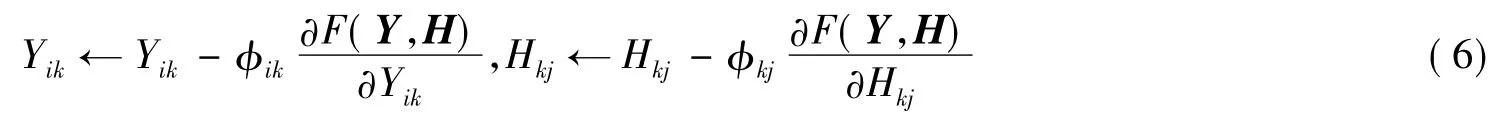
分别计算F(Y，H)关于Yik和Hkj的偏导数：

取步长为：

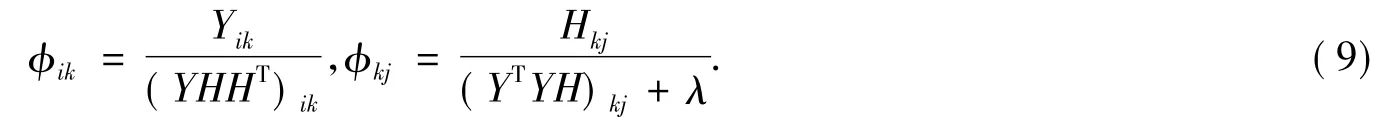
将(7)(8)(9)代入(6)中分别求得：

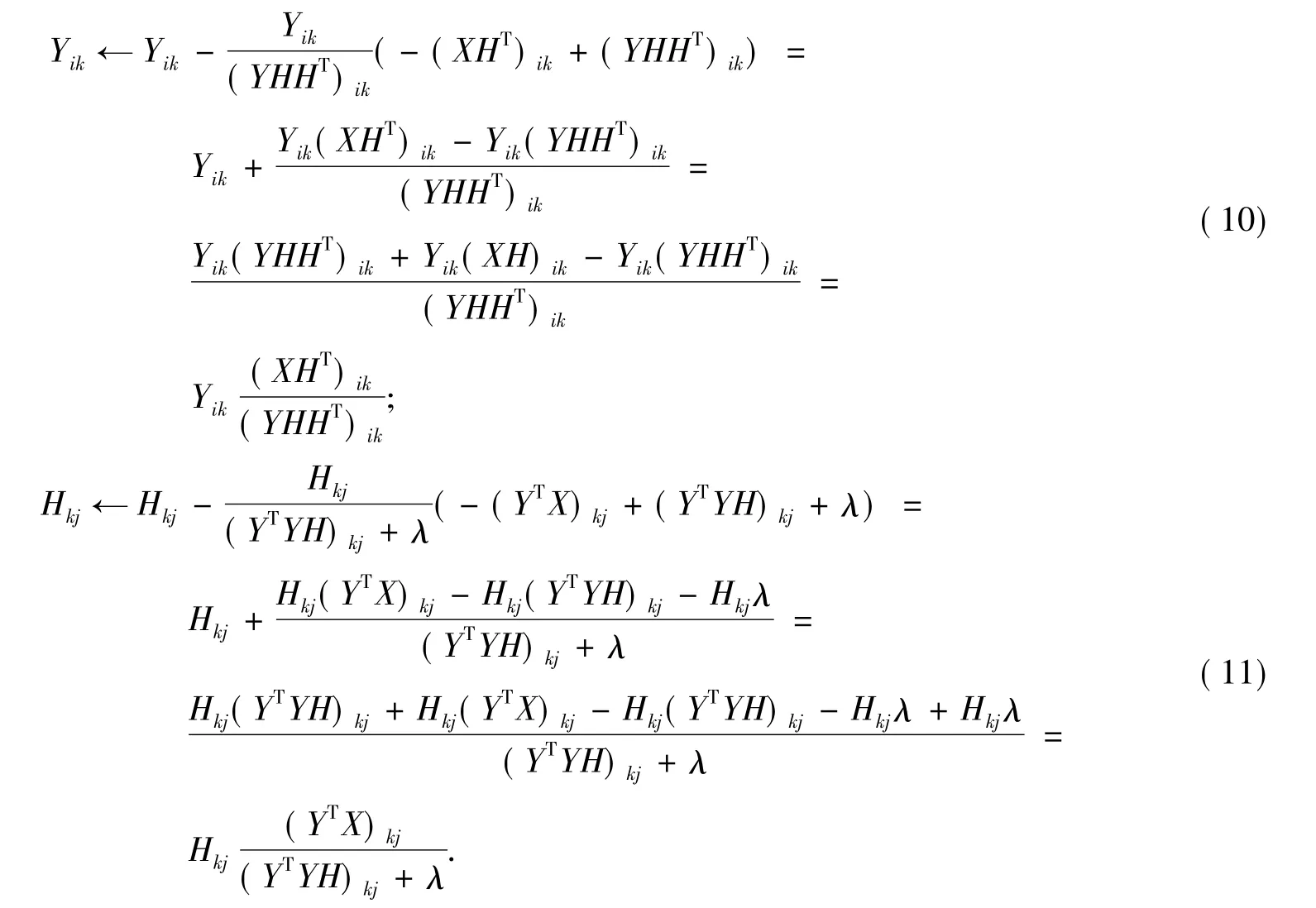
2.2 收敛性分析

引入文献［2］中的定义和引理来证明(10)和(11)的收敛性．

定义1 称函数G(h，h')为函数F(h)的辅助函数，如果满足以下2个条件：

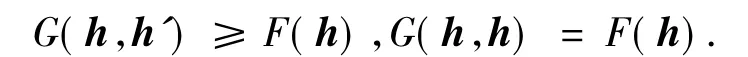
引理1 如果函数G(h，h')为函数F(h)的辅助函数，则按下式迭代，函数F(h)是非增的：

此引理能保证目标函数F非增，

定理1 函数

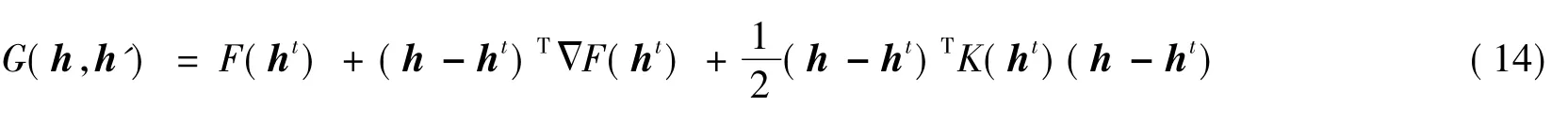
这里h表示矩阵H中的某一列，hi表示该列的第i个元素，x表示矩阵X中相应的列．显然G(h，h)=F(h)．比较式(14)与下式

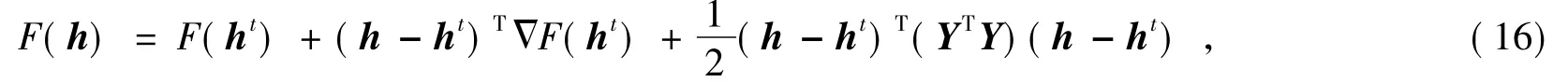
如果G(h，h')≥F(h)，须使0

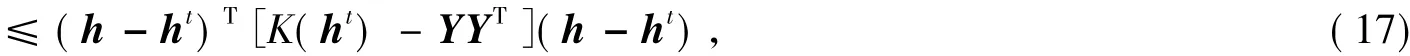
当(15)式中λ=0时，Lee和Seung已证明式(17)的正确性．当λ＞0时，对角矩阵K可看成是2个半正定的矩阵的和．所以同理也可以证明式(17)的正确性．

定理2 利用迭代规则(10)和(11)交替求解Y和H时，目标函数(5)非增，且函数值不再变化的条件是当且仅当Y和H是式(5)的稳定点．

证明 由于G(h，h')是F(h)的辅助函数，根据引理，只需最小化G(h，ht)，即令

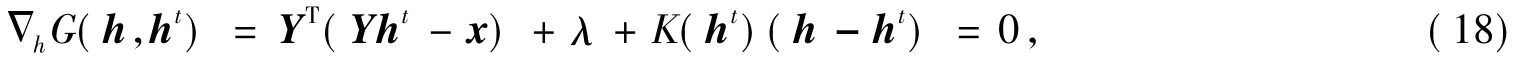
解之，得：

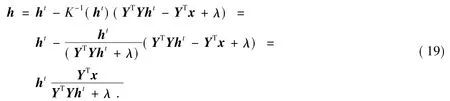
写成矩阵元素形式为：

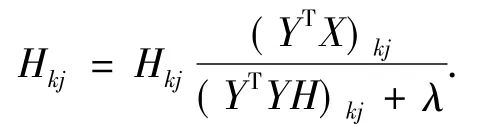
F(y)在关于矩阵Y的迭代规则式(10)下的非增和Lee的证明类似，就不再给出证明．

2.3 算法步骤

根据以上阐述，本文给出非负矩阵分解的快速稀疏算法的步骤如下：

Step1：在V=WH的两边左乘VT，得VTV=VTWH，令VTV=X，VTW=Y，则又可得X=YH;

Step2：在非负条件下对Y和H随机赋初值;

Step3：更新Y和H，其更新规则为式(10)和式(11);

Step4：重复Step3直到目标函数式(5)收敛．

2.4 实验及分析

2.4.1 分解速度

任意给定一个矩阵 V=rand(500，80)，我们取r=30时，对NMF算法和FSNMF算法得到H矩阵随迭代次数增加所需时间列表分析，如表1．

由表1我们可以看出，同样的一个矩阵V，FSNMF算法得到H矩阵的分解速度要比NMF算法得到H矩阵的速度快的多．

2.4.2 稀疏性

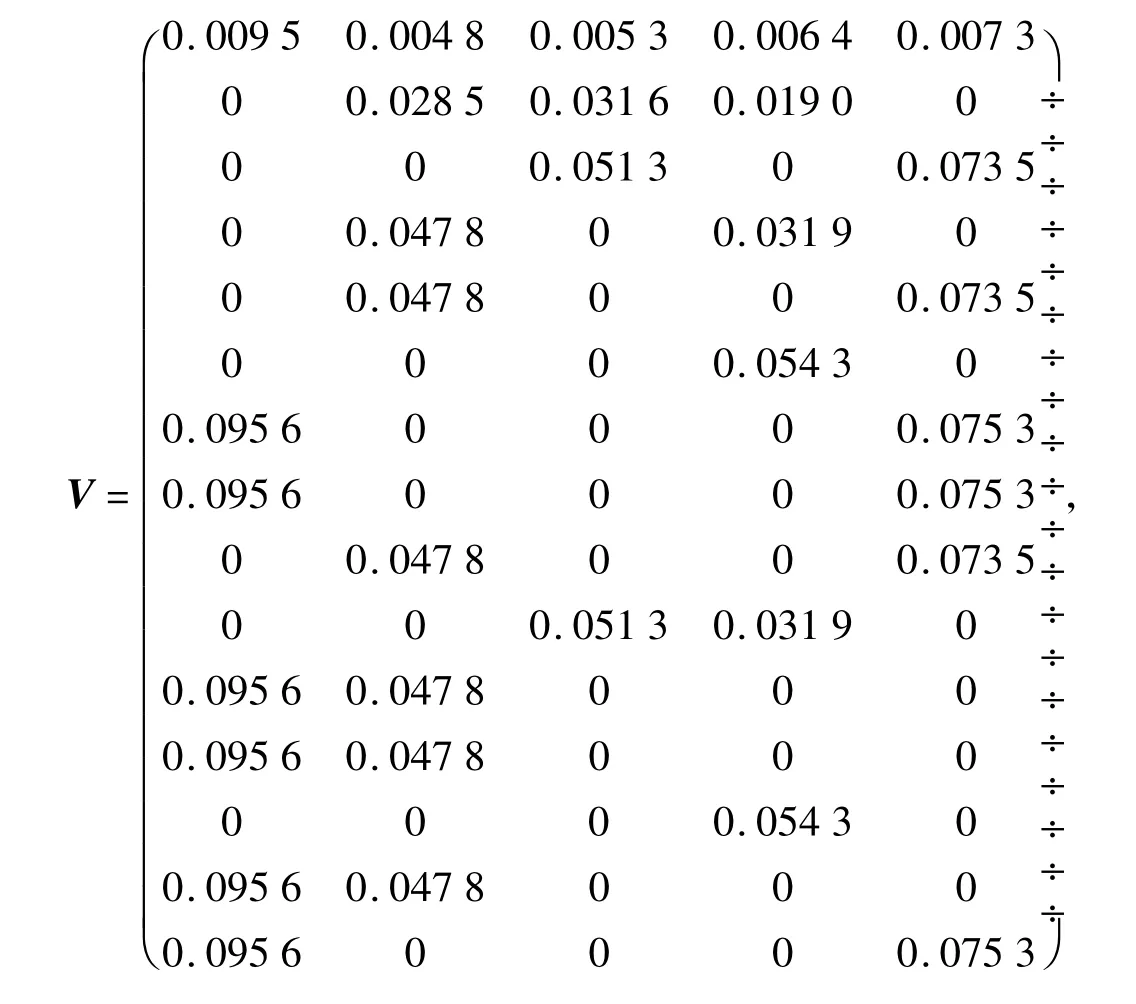
给定一个文本矩阵我们对V按照本文给出的FSNMF算法进行分解，取r=3时，并且控制λ值的大小观察所得H矩阵中元素为0的个数．我们列表分析，如表2．

表2 稀疏度表

由表2我们可以看出，适当的λ值能够得到矩阵H较高的稀疏性，合适的稀疏度有利于保留数据的主要特征，学习更清楚的局部特征，还可以减少储存空间．

2.4.3 文本文摘举例

给定一段文章如下：教学具有多种形态，是共性和多样性的统一．教学作为学校进行全面发展教育的一个基本途径，具有课内、课外、班级、小组、个别化等多种形态．教师和学生共同进行的课前准备、上课、作业、练习、辅导、评定等都属于教学活动．随着社会的发展，教学既可以通过师生间、学生间的各种交往进行，也可以通过印刷、广播、电视、录音、录像等远距离教学手段开展．教学作为一种活动，一个过程，是共性与多样性的统一．

对这段文章运用Lee等［6］提出的文摘方法，并把求H矩阵的算法部分改为本文提出的FSNMF算法去求H矩阵，最后得到的每个句子的相关度为：

GRS=(1．0e －003) ×〔0．475 1 0．118 6 0．029 1 0．011 2 0．308 0〕．

由此，可以判断出第1句是最重要的句子，其次是第5句．所以这一段的文摘句就为：教学具有多种形态，是共性和多样性的统一．

由此例，可以看到将非负矩阵分解的快速稀疏算法应用于文本分析能够快速准确地得到文章的文本文摘．

3 结语

本文提出的非负矩阵分解的快速稀疏算法，通过代数变换使得数据进行降维，在目标函数中附加约束稀疏度的稀疏项从而定义了目标函数，并且给出了迭代规则和收敛性证明．并且举例说明了此算法使得矩阵的分解速度和稀疏度都有所提高，又进一步利用此算法进行了一个简单的文本文摘，准确地得到了文摘的结果．

［1］LEE D D，SEUNG H S．Learning the parts of objects by non －negative matrix factorization［J］．Nature，1999，401(6755)：788 －791．

［2］ LEE D D，SEUNG H S．Algorithms for non －negative matrix factorization［C］//Advances in Neural Information Processing Systems 13．Cambridge：MIT Press，2001：556 －562．

［3］ 李乐，章毓晋．非负矩阵分解算法综述［J］．电子学报，2008，37(4)：737 －743．

［4］王文俊，张军英．一种非负矩阵分解的快速方法［J］．计算机工程与应用，2009，45(25)：1－2，6．

［5］ HOYER P O．Non－negative matrix factorization with sparseness constraints［J］．J Mach Learning Res，2004，5(9)：1 457－1 469．

［6］LEE J H，PARK S，AHN C M，et al．Automatic generic document summarization based on non－negative matrix factorization［J］．Information Processing and Management，2009，45：20 －34．