电磁感应现象中的释疑

卢冬阳

(九江市同文中学 江西 九江 332000)

笔者在高三物理复习课的教学中，遇到了一道如下的电磁感应的习题，此题在许多资料上也出现过．

【例题1】一个半径为r的圆形铝环由静止开始在水平均匀向外辐射的磁场中下落，设下落时圆环平面始终保持水平，圆环处的磁场的磁感应强度大小为B，如图1所示.已知圆环的铝线半径为r0，密度为ρ0，电阻率为ρ．磁场范围足够大.试求圆环下落的稳定速度．

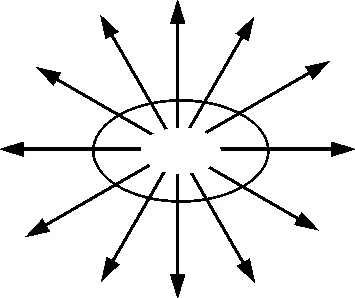
图1

解析：铝环的周边都切割磁感线，在环内产生顺时针方向的感应电流，圆环因而受到竖直向上的安培力的作用．当安培力与铝环的重力平衡时，便达到稳定的竖直向下的速度v.根据法拉第电磁感应定律、闭合电路欧姆定律、电阻定律及平衡条件可得

E=B2πrv

F安=BI2πr

F安=mg

m=ρ02πrπr02

由以上6式联立解得圆环下落的稳定速度

解后学生立即提出疑问：

(1)这样的磁场存在吗？磁感线如何形成封闭曲线？

(2)对于铝环而言，只有横向的向外辐射磁场，在铝环下落过程中，穿过线环的磁通量不发生改变，若产生了感应电流，这不与法拉第电磁感应定律相矛盾吗？

针对以上问题，笔者引入了另一道习题.

【例题2】一个质量为m，直径为d，电阻为R的金属圆环，在范围足够大的磁场中竖直下落.金属环在下落过程中的环面始终保持水平，磁场的分布与圆环的中心轴线对称如图2所示.已知磁感应强度的竖直分量By的大小只随高度y变化，其变化关系为By=B0(1+ky)．其中k为大于零的常量．金属环在下落过程中，速度越来越大，最终稳定为某一数值，称为收尾速度．求:

(1)圆环收尾速度的大小．

(2)圆环达到收尾速度时，磁感应强度在圆环处沿直径方向分量大小将不变，设为Bx，则Bx为多大.

图2

解析：(1)设圆环中感应电动势为E，由法拉第电磁感应定律得

(1)

当vy达到最大速度vm时，有

得收尾速度

(2)由动生电动势得

E=Bxπdvy

(2)

结合(1)式得

仔细分析，例题1与例题2有着十分密切的内在联系.例题2的磁场与条形磁铁的磁极周围的磁场相近.如果例题1的磁场在竖直方向存在分量，则与例题2相似;例题1中学生的问题就迎刃而解了．但是，对于例题2学生又有了新的疑问.

圆环在下落过程中，穿过圆环回路磁通量在y方向上增加又在径向切割磁感线，而产生的电动势为什么不是(1)、(2)两式相加呢？

同学们可能把磁场沿y方向的随空间位置而变，理解成了磁场沿y方向的改变为随时间而变，未能理解该磁场是静磁场的确切含义．这里只有动生电动势而没有感生电动势．于是笔者又引入了以下第二道习题.

【例题3】如图3所示，水平面内有长直平行的光滑导轨，间距为L，其上方正交放置两平行金属杆ab、cd．空间存在竖直向下的匀强磁场，磁感应强度大小为B．当ab、cd分别以等大的速率v向相反的方向垂直于杆匀速运动时，求回路中的感应电动势的大小．

图3

解析：问题一提出，同学们马上求出了整个电路中感应电动势的大小为

E=E1+E2=2BLv

(3)

或者

(4)

这个问题比较简单，学生对以上结果坚信不疑．这时笔者则加问了一句：我们为什么不把感应电动势写成(3)、(4)两式之和呢？此时同学们恍然大悟，其中有许多同学踊跃发言.原来是因为当ab、cd金属杆切割了磁感线，使闭合回路的面积发生了变化，才使回路的磁通量发生了改变.以上两种做法是等效的．在此基础上，笔者顺水推舟，再引导学生对于例题3中如果ab、cd金属杆在切割磁感线的同时，空间磁场又随时间线性增加，如何求出感生电动势及动生电动势的和．

以上三例，在例1中同学们之所以有疑问，是由于题目给的磁场相当于磁单极子的磁场，实际上不存在，因而推出了矛盾的结论;例题2和例题3则是教师为了进一步释疑而引出的思维拓展．电磁感应及其应用是高考的热点内容之一;在习题教学中，教师要善于抓住学生的疑点，将同类疑点归类剖析，循序渐进层层释疑，对提高学生的质疑、释疑能力及独立分析解决问题的能力将大有益处．